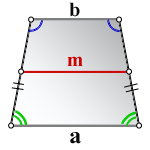
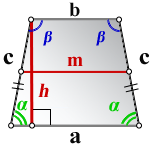
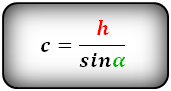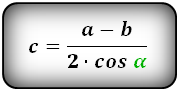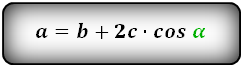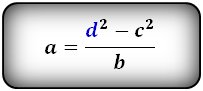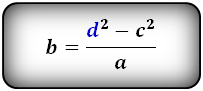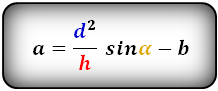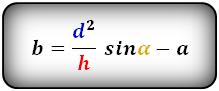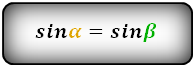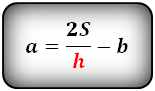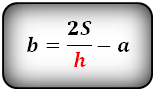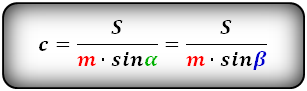1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
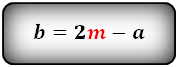
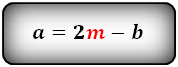
Формулы длины основания:
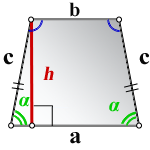
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
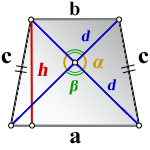
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
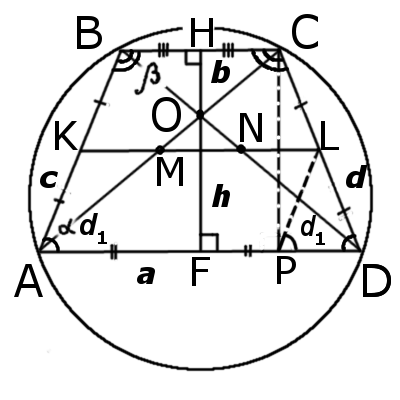 |
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
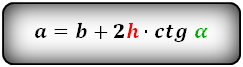
a = b + 2h ctg α = b + 2c cos α
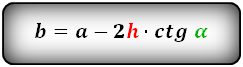
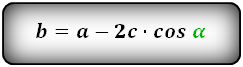
b = a — 2h ctg α = a — 2c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 — c2 | b = | d12 — c2 | c = √d12 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a — h ctg α = b + h ctg α = a — √c2 — h2 = b + √c2 — h2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 — 2ac cos α
d1 = √b2 + c2 — 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию:
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 — (a — b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a — c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
Вот, что нужно для этого знать:
- длину обоих оснований трапеции;
- высоту трапеции.
И еще вам понадобится:
- лист бумаги;
- карандаш;
- линейка.
Постройте трапецию ABCD. При этом ее боковые стороны равны между собой. Проведите две высоты из верхних точек. Получим два одинаковых треугольника. Чтобы найти сторону трапеции, нужно найти сторону треугольника, которая прилегает к прямому углу. Для этого вычитаем из большего основания меньшее и делим на 2.
Теперь по теореме Пифагора вычисляем гипотенузу в треугольнике. Гипотенуза = корень квадратный из суммы произведений катетов. В нашем случае один катет — это высота, а второй мы с вами нашли в предыдущем пункте.
Как найти боковые стороны равнобедренной трапеции
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны называются основаниями. Их конечные точки соединены отрезками, которые называются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.

Вам понадобится
- — равнобедренная трапеция;
- — длины оснований трапеции;
- — высота трапеции;
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
Постройте трапецию согласно условиям задачи. Вам должны быть даны несколько параметров. Как правило, это оба основания и высота. Но возможны и другие условия — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пусть будут a и b, высоту обозначьте как h, а боковые стороны — х. Поскольку трапеция равнобедренная, боковые стороны у нее равны.
Из вершин B и С проведите высоты к нижнему основанию. Точки пересечения обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, поскольку по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой. Обозначьте их длину как y.
Для того, чтобы найти длину суммы этих отрезков, необходимо из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет равен разности оснований, деленной на 2. y=(a-b)/2.
Найдите длину боковой стороны трапеции, которая одновременно является и гипотенузой прямоугольного треугольника с известными вам катетами. Вычислите ее по теореме Пифагора. Она будет равна квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=√y2+h2=√(a-b)2/4+h2.
Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не нужно. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN или x=h*sinBAM.
Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, найдите нужный угол, исходя из свойства параллельных прямых. Вспомните одно из свойств равнобедренной трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание
Повторите свойства равнобедренной трапеции. Если разделить оба ее основания пополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.
Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Например, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а другой — половине их разности.
Источники:
- в равнобедренной трапеции основания найти боковые стороны
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
 |
| Рис.1 |
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a — 2 h ctg α = a — 2 c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 — c 2 | b = | d 1 2 — c 2 | c = √ d 1 2 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
m = a — h ctg α = b + h ctg α = a — √ c 2 — h 2 = b + √ c 2 — h 2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 — ( a — b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
d 1 = √ a 2 + c 2 — 2 ac cos α
d 1 = √ b 2 + c 2 — 2 bc cos β
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √ 4 c 2 — ( a — b ) 2 |
| 4 |
2. Формула площади через стороны и угол:
S = ( b + c cos α ) c sin α = ( a — c cos α ) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя: