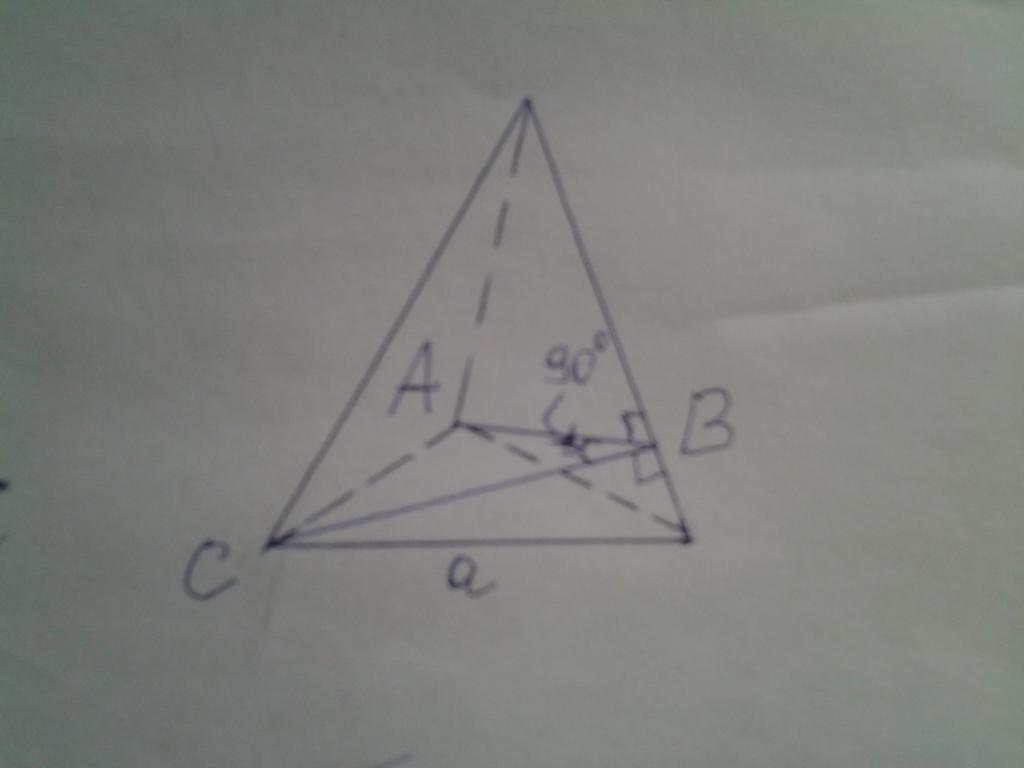Как найти боковой кант пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

апофема правильной треугольной пирамиды равна 15 см, а отрезок, соединяющий вершину пирамиды с центром основания, -12 см, найдите:а) боковой кант и сторону основы пирамиды, б) боковую поверхность пирамиды,в) полную поверхность пирамиды.

Источник

а) Апофема DК = 15 см, высота DО = 12 см. Точка О — центр основания пирамиды — точка пересечения медиан правильного треугольника АВС.
Треугольник DОК — прямоугольный, по т Пифагора
$OK= sqrt{ DK^{2}-DO ^{2} }= sqrt{225-144}=9$ cм. ВК делится точкой О на отрезки в отношении 2:1, считая от вершины. Отсюда ВК = 3 ОК = 27 см.
Так как $BK= frac{a sqrt{3} }{2}, a= frac{2BK}{ sqrt{3} }= frac{54}{ sqrt{3} }=18 sqrt{3}$ .
ОВ = 2/3 ВК = 2/3 * 27 = 18 см.
Из прямоугольного треугольника DOB найдем боковое ребро DB.
По т Пифагора $DB= sqrt{DO ^{2}+ BO^{2} }= sqrt{144+324}= sqrt{468}=6 sqrt{13}$ см
б) Найдем боковую поверхность пирамиды $S _{1} = frac{1}{2} P*DK$
$S= frac{1}{2}*3*18 sqrt{3}*15=405 sqrt{3}$
в) Полную поверхность найдем по формуле $S= S _{ABC} +S _{1}$
$S _{ABC} = frac{a ^{2} sqrt{3} }{4} = frac{972* sqrt{3} }{4}=243 sqrt{3}$ кв см
кв см

Источник

Апофема правильной треугольной пирамиды равна 15 см, а отрезок, соединяющий вершину пирамиды с центром основания, — 12 см, найдите : а) боковой кант и сторону основы пирамиды, б) боковую поверхность пирамиды, в) полную поверхность пирамиды.

На этой странице находится вопрос Апофема правильной треугольной пирамиды равна 15 см, а отрезок, соединяющий вершину пирамиды с центром основания, — 12 см, найдите : а) боковой кант и сторону основы пирамиды, б) боковую поверхность п?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Источник

Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.

Если в основании лежит квадрат, то пирамиду называется четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:

Рассмотрим пример расчета площади боковой поверхности пирамиды.

Пусть дана пирамида с основанием ABCDE и вершиной F. AB=BC=CD=DE=EA=3 см. Апофема a = 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды: $S_bok={1/2}*15*5=37,5{cm}^2$

Площадь правильной треугольной пирамиды

Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.

Дана пирамида с апофемой a = 4 см и гранью основания b = 2 см. Найдите площадь боковой поверхности пирамиды.
Для начала находим площадь одной из боковых граней. В данном случае она будет:
Подставляем значения в формулу: $S={1/2}*4*2=4{cm}^2$
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:
S=3S_gr
$S=3*4=12{cm}^2$

Площадь усеченной пирамиды

Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
$S=1/2{(p_1+p_2)}a$

Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.

Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь: $S=1/2 {(20+12)}*4={32/2}*4=64{cm}^2$

Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.

Источник

Задача

В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.

Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2

Треугольник OKN — прямоугольный, OK — высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как α .

tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°

Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.

Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как β ) равен

tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°

Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°

Двугранные углы пирамиды и методика их расчета

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Вам будет интересно: Популяция людей: определение, виды, свойства и примеры

Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

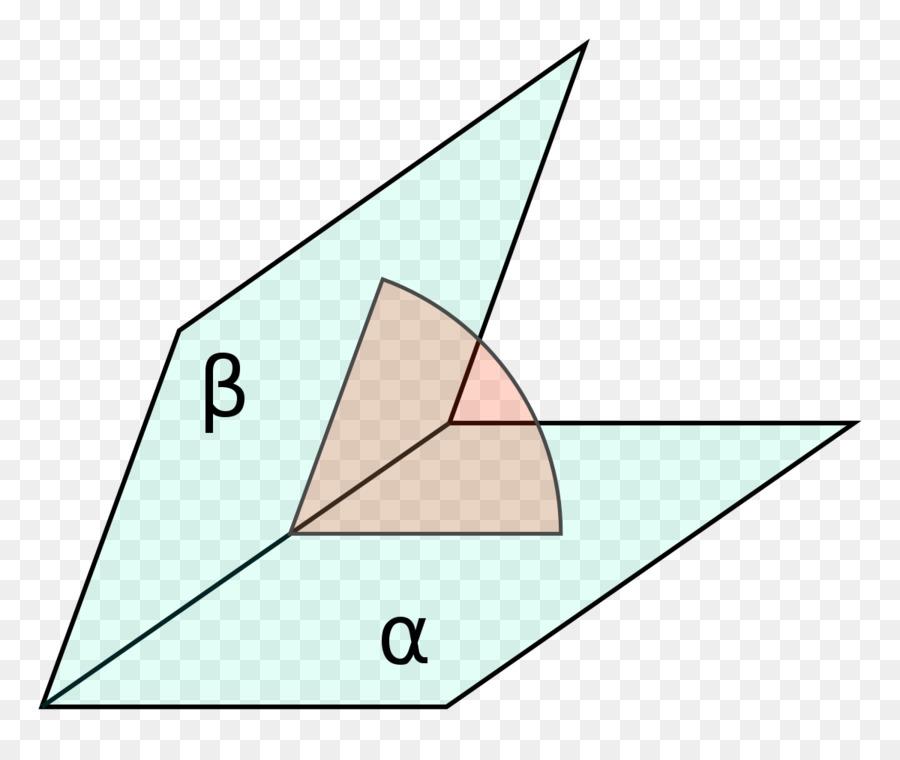
Двугранные углы фигуры

Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.

Как рассчитать углы пирамиды?

Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

Или в координатной форме:

φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

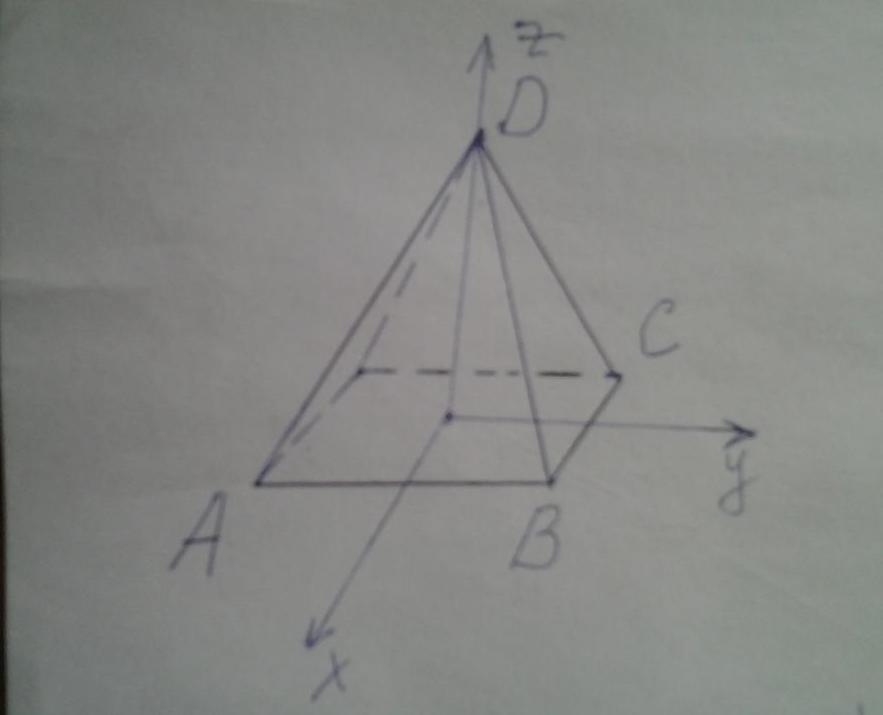
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

Угол между ABD и BDC:

φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — hb и боковое ребро — b. Теперь можно записать следующие формулы:

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

Площадь равностороннего треугольника рассчитывается так:

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.

Пирамида и ее элементы

Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.

Рассмотрим плоскость alpha , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.

Пирамида называется правильной, если правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.

Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.

Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.

Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA

Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.

Формула объема пирамиды:
1) $V=frac<1> <3>cdot S_ <OCH>cdot h» />, где <img decoding=$ -высота пирамиды
2) $V=frac<1> <3>cdot r cdot S_<0>» />, где <img decoding=$ – радиус вписанного шара, а S_0 – площадь полной поверхности пирамиды.
3) $V= frac<2> <3>cdot MN cdot S_0″ />, где MN – расстояние любыми двумя скрещивающимися ребрами, а <img decoding=$ – площадь параллелограмма, образованного серединами четырех оставшихся ребер.

Свойство основания высоты пирамиды:

Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням

Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.

Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте

Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны implies все проекции боковых ребер будет равны implies P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.

Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней .
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле , где p — полупериметр основания, а SK-апофема.

Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.

Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.

Колпаков Александр,
репетитор по математике в Москве. Строгино

Источник