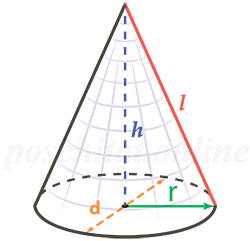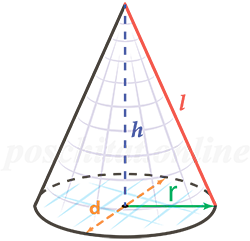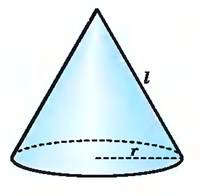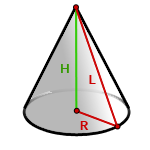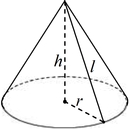
Как найти боковую поверхность конуса через образующую - Исправление недочетов и поиск решений вместе с Examum.ru

Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.

Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.

Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.

Радиус конуса – это радиус его основания.

Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.

Формула образующей конуса

Образующую конуса можно найти, зная ее высоту H и радиус R:

L = √H² + R²

Формула площади боковой поверхности конуса

Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:

S_{бок.пов} = πRL

Формула площади основания конуса

Площадь основания конуса можно вычислить по его радиусу R:

S_осн = πR²

Формула площади конуса

Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:

S = S_{бок.пов} + S_осн = πRL + πR²

Формула объема конуса

Объем конуса можно вычислить, зная его высоту H и площадь основания:

V = 1/3 ⋅ S_осн ⋅ H = 1/3πR²H

Источник

Площадь поверхности конуса

Главная
/
Математика
/
Геометрия
/
Площадь поверхности конуса

Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Площадь боковой поверхности конуса

=
=

S_б.пов =

Округление числа π: Округление ответа:

Площадь полной поверхности конуса

=
=

S_п.пов =

Округление числа π: Округление ответа:

Просто введите данные, и получите ответ.

Теория

Площадь боковой поверхности конуса через образующую

Чему равна площадь боковой поверхности конуса S_б.пов, если образующая l, а радиус основания r:

Формула

S_б.пов = π ⋅ r ⋅ l

через диаметр:

S_б.пов = π ⋅ l ⋅ ^d⁄₂

Пример

Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:

S_б.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²

Площадь боковой поверхности конуса через высоту

Чему равна площадь боковой поверхности конуса S_б.пов, если высота h, а радиус основания r:

Формула

S_б.пов = π ⋅ r ⋅ √r² + h²

через диаметр:

S_б.пов = π ⋅ ^d⁄₂ ⋅ √(d/2)² + h²

Пример

Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:

S_б.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²

Площадь полной поверхности конуса через образующую

Чему равна площадь полной поверхности конуса S_п.пов, если образующая l, а радиус основания r:

Формула

S_п.пов = π ⋅ r ⋅ (r + l)

через диаметр:

S_п.пов = π ⋅ ^d⁄₂ ⋅ (^d⁄₂ + l)

Пример

Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:

S_п.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²

Площадь полной поверхности конуса через высоту

Чему равна площадь полной поверхности конуса S_п.пов, если высота h, а радиус основания r:

Формула

S_п.пов = π ⋅ r ⋅ (r + √r² + h²)

через диаметр:

S_п.пов = π ⋅ ^d⁄₂ ⋅ (^d⁄₂ + √(d/2)² + h²)

Пример

Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:

S_п.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²

См. также

Источник

Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Треугольник (POA) вращается вокруг стороны (PO).

(PO) — ось конуса и высота конуса.

(P) — вершина конуса.

(PA) — образующая конуса.

Круг с центром (O) — основание конуса.

(AO) — радиус основания конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.

Осевое сечение конуса — это равнобедренный треугольник.

(APB) — осевое сечение конуса.

∡PAO=∡PBO

— углы между образующими и основанием конуса.

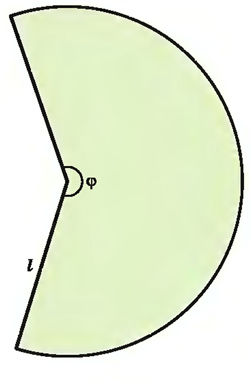
Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса

2πR

, угол развёртки боковой поверхности

В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.

Образующая конуса (l) является радиусом сектора.

Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):

Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).

Сравним выражения длины дуги и выразим

через (R):

2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.

Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:

Sбок.=πl2⋅R⋅360°360°⋅l=πRl

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

OO1

— ось конуса и высота конуса.

Круги с центрами (O) и

— основания усечённого конуса.

(AO) и

A1O1

— радиусы оснований конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось

OO1

конуса.

Осевое сечение конуса — это равнобедренная трапеция.

AA1B1B

— осевое сечение конуса.

Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:

Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.

Так как

ΔPAO∼ΔPA1O1

, то стороны их пропорциональны:

PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.

Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:

Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.

Источник

Теорема: Площадь боковой поверхности конуса равна произведению полуокружности его основания и образующей.

Доказательство.

Пусть имеется конус, радиус основания которого равен r, а образующая I (рисунок).

Развернем боковую поверхность конуса на плоскость, в результате получится сектор, радиус которого равен образующей I (рисунок ниже).

Найдем центральный угол ϕ этого сектора, приняв во внимание, что ему соответствует дуга окружности, равная длине окружности основания конуса, т. е. равна 2πr. Поскольку длина всей окружности, связанной с сектором, равна 2πl и этой длине соответствует полный угол, равный 360°, то

Теперь найдем площадь S сектора с радиусом I и углом ср:

Поскольку выражение πr представляет длину полуокружности основания конуса, можем утверждать, что площадь боковой поверхности конуса равна произведению полуокружности его основания и образующей.

Источник