Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b — катеты, с — гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b — катеты, с — гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a — искомая сторона, S — площадь треугольника.
2) Найти сторону через высоту
где a — искомая сторона,h — высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a — искомая сторона,r — радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a — искомая сторона,R — радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a — искомая сторона, b — известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Как посчитать стороны равнобедренного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10 /2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания , а высота
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √ 1 /10 2 + 20 2 = √ 0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны , а высота
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅ √ a 2 — h 2 , h
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Боковая сторона равнобедренного треугольника
У равнобедренного треугольника 2 равных по длине стороны. Каждая из них — боковая сторона равнобедренного треугольника, а третья будет основанием. Их часто просят найти при решении различных задач в геометрии. Зная основные способы решения, формулы, теоремы и свойства геометрической фигуры, учащийся может легко справиться с предложенным заданием.
Основные свойства
Свойства основания равнобокого треугольника применяются на практике. Фигуру будет проще воспринимать визуально, если расположить чертеж таким образом, чтобы основание располагалось снизу.
Принято считать, что равносторонний треугольник — это частный случай равнобедренного. Каждая его сторона может считаться и основанием, и боковой.
Помимо равенства боковых сторон, при решении задач используют совпадение биссектрисы с высотой. Решить задание, как найти основание равнобедренного треугольника, зная боковые стороны, невозможно в следующих случаях:
- Известно лишь основание или углы.
- По условию дана только величина характеризующих отрезков — биссектрисы, высоты.
А также решение задачи невозможно, если заданы только две боковые стороны. В остальных случаях найти решение можно, даже если известен только один угол или площадь.
Важная теорема
Для решения задач на построение, когда задана боковая сторона треугольника, используется теорема, связанная с высотой. Применяется она и для медианы с биссектрисой.
Ее суть в следующем:
- Биссектриса, которая проведена к основанию, будет не только высотой. Она считается и медианой.
- Высота, проведенная к основанию, не только медиана. А также она может быть названа биссектрисой.
- Медиана, которая проведена к основанию, будет не только высотой, но и биссектрисой.
Теорема доказывается следующим образом: если в заданном треугольнике ABC из точки B провести высоту BD, он будет разделен на треугольники ABD и CBD. Помимо общего катета, у них равны гипотенузы. Что касается прямых AC и BD, они будут перпендикуляром.
Получается, что в ABD и CBD углы BAD и BCD, а также AB и BC равны. А также — AD и CD. Следовательно, фигуры равны, а BD считается как высотой, так и медианой и биссектрисой.
Полезные формулы
Когда по условию не даны углы, но известны все стороны, поможет формула для косинусов: cos A = (b² + с² — а²)/ 2bc = (b² + a² — а²)/2ba = b²/2ba = b/2a. При этом cos В = (а² + а² — b²)/ 2bc = (b² + a² — а²)/2а² = (2 a² — b²)/2а².
Медиана вычисляется по следующей формуле: √(2 a² + 2b² — а²)/2 = √(a² + 2b²)/2. Биссектрису можно вычислить с помощью формулы √ ab (2a+b)(a+b-a)/(a+b) = b√ a (2a+b)/(a+b).
Средняя линия, параллельная основанию равнобедренного треугольника, считается равной его половине. Равны между собой и средние линии, которые параллельны его боковым сторонам.
Если необходимо вычислить радиус описанной вокруг равнобедренного треугольника окружности, используется формула R = a²/√(4а² — b²). Когда окружность вписана в фигуру действует формула r= b/2√(2a-b)/(2a+b).
Примеры решения задач
Вот примеры заданий, как узнать боковую сторону равнобедренного треугольника АВС. Так, если основание АС = 8 см, а опущенная на его середину высота (являющаяся медианой) BH =3 см, то AH = AC = 4 см. По теореме Пифагора боковая сторона AB = √ AH ² + BH ² = √ 16+9 = √25 = 5 см.
Можно привести и следующий пример задачи. Если площадь равнобедренного треугольника АВС = 40√ 3 см², а углы при основании (A и C) = 30°, угол B будет равен 180° — 2 * ∠АС = 180° — 2 * 30° = 120°.
В этом случае действует формула S = ½ АВ*АС * sin ∠B = ½ * AB ² * sin 120° = 40√ 3 см². Значит, AB ² = 2*40√ 3/ sin 120 = 80 √ 3:√ 3/2 = 160. Тогда АВ = 4√ 10 см.
Еще пример задачи — если боковая сторона равна 1, а угол при вершине 120°, диаметр окружности, описанной вокруг него, можно найти так: угол при основании будет равен (180−120)/2, то есть 30°. В таком случае диаметр будет 1/sin 30° = 2 см.
Задачи, связанные с нахождением боковой стороны треугольника, часто встречаются в геометрии. Для их решения необходимо знать перечисленные формулы и свойства.
http://www-formula.ru/2011-10-09-11-08-41
http://prostudenta.ru/article-2254.html
Совсем неплохо , если бы вы дали хотя какие-то данные .Что дано?
1) Если дано основание а , и высота h , проведённая к этому основанию , то боковая сторона b равна ( находим по теореме Пифагора :
b ^2 = ( a /2)^2 + h^2 ) , после подсчёта извлечём из суммы квадратов корень.
2)Если дано основание а ,и угол при основании А , тогда боковая сторона находится с помощью тригонометрических формул , применимых для заданного угла А.
b = ( a/2 )/ ( cos <A ),
3)Возможны другие данные заданы.Если будет известен угол при вершине В , и основание а , то тоже через тригонометрические формулы.
b = ( a/2 ) / sin ( B/2 ) , и так далее , нужны данные.
Стороны равнобедренного треугольника
Стороны фигур
Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны в таком треугольнике называются боковыми, третья — основанием. Периметр равнобедренного треугольника (Р) будет равен сумме двух одинаковых боковых сторон (а) и основания (b):
Р = 2а + b
Против равных сторон лежат равные углы. Перпендикуляр, опущенный из вершины треугольника к его основанию, называется высотой равнобедренного треугольника. Проведенные к основанию биссектриса, медиана и высота совпадают между собой, делят треугольник на 2 равных прямоугольных треугольника, гипотенузой которых будет боковая сторона (а), а катетами — высота (h) и половина основания равнобедренного треугольника (b/2). По теореме Пифагора квадрат гипотенузы равен сумме квадратов его катетов, в нашем случае квадрат боковой стороны а (как гипотенузы) равен сумме половины основания (b/2), возведенного в квадрат, и высоте h в квадрате:
а2 = (b/2)2+h2
Отсюда, боковая сторона будет равна корню из суммы половины основания в квадрате и высоты, также возведенной в квадрат:
а = √(b/2)2+h2,
где а — боковая сторона, b/2 — половина основания, h — высота.
Если в прямоугольном треугольнике известна гипотенуза (в нашем случае это боковая сторона равнобедренного треугольника — а) и один из катетов (высота h), неизвестный катет находим, воспользовавшись теоремой Пифагора. Заметим, что неизвестный катет является половиной основания равнобедренного треугольника (b/2). Тогда, квадрат катета прямоугольного треугольника равен квадрату гипотенузы минус квадрат другого катета:
(b/2)2 = a2 — h2
Половина основания треугольника (b/2) равняется корню квадратному из квадрата гипотенузы минус квадрат другого катета:
b/2 = √а2 — h2,
где b/2 — половина основания, а — боковая сторона, h — высота.
Умножив полученный результат на 2, находим всю длину основания.
Расчет длины стороны равнобедренного треугольника зная сторону и высоту
Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.
- Сторона треугольника равностороннего через радиус описанной
окружности - Сторона треугольника равностороннего через радиус вписанной
окружности - Сторона треугольника равностороннего через высоту
- Сторона треугольника равностороннего через площадь
треугольника - Основание равнобедренного треугольника через боковые
стороны и угол между ними - Основание равнобедренного треугольника через боковые
стороны и угол при основании - Боковая сторона равнобедренного треугольника через
основание и угол между боковыми сторонами - Боковая сторона равнобедренного треугольника через
основание и угол при основании - Катет прямоугольного треугольника через гипотенузу и острый
угол - Катет прямоугольного треугольника через гипотенузу и другой
известный катет - Гипотенуза прямоугольного треугольника через катет и острый
угол - Гипотенуза прямоугольного треугольника через катеты
- Сторона треугольника через две известные стороны и угол
между ними - Сторона треугольника через известную сторону и два угла
Сторона равностороннего треугольника через радиус описанной окружности
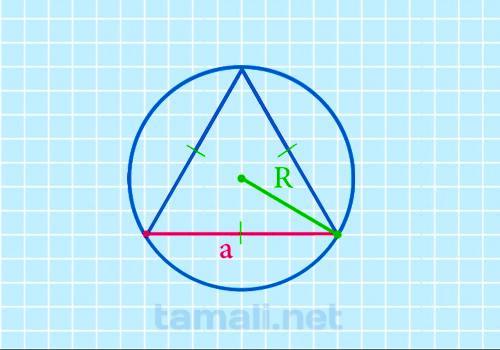
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:
a = R * √3
где а — сторона треугольника, R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.
Сторона равностороннего треугольника через радиус вписанной окружности
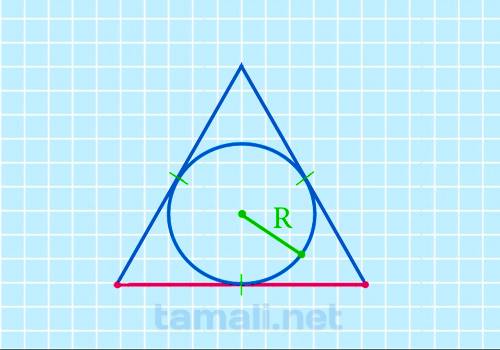
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):
a = 2r * √3
где а — сторона треугольника, R — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.
Сторона равностороннего треугольника через высоту
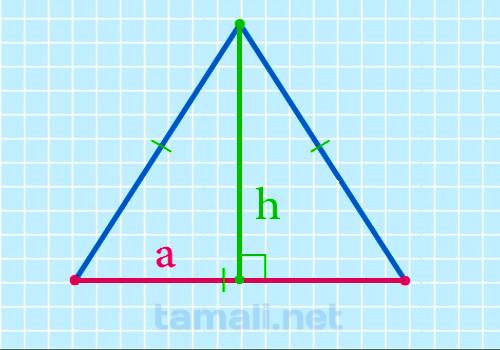
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:
a = 2h / √3
где а — сторона, h — высота равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.
Сторона равностороннего треугольника через площадь
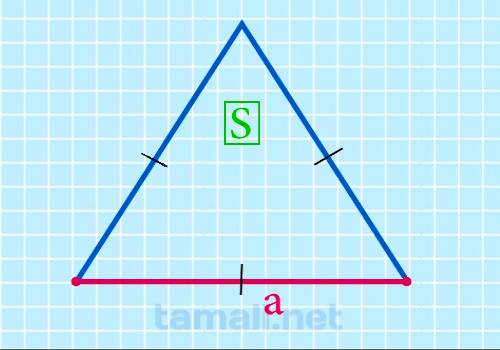
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу
a = √(4S / √3)
где а — сторона, S — площадь равностороннего треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.
Основание равнобедренного треугольника через боковые стороны и угол между ними
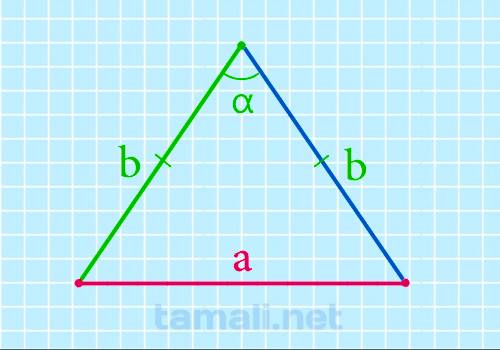
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:
a = 2b * sin (α/2)
где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.
Основание равнобедренного треугольника через боковые стороны и угол при основании
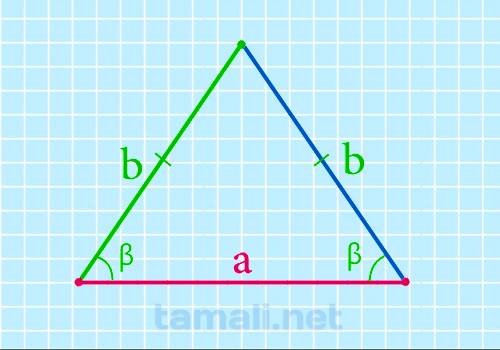
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:
a = 2b + cos β
где b — боковая сторона, β — угол при основании.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.
Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами
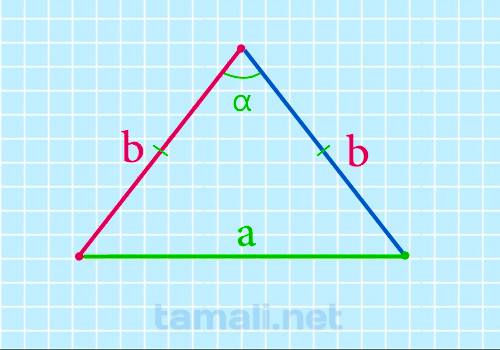
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным. Это значит, что α = β.
Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:
b = a / (2 * sin(α/2))
где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.
Цифр после
запятой:
Результат в:
Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.
Боковая сторона равнобедренного треугольника через основание и угол при основании
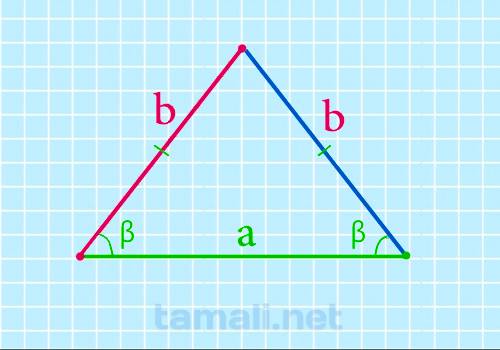
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:
b = a / 2 * cos β
где a — это основание, β — угол при основании равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.
Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.
Катет прямоугольного треугольника через гипотенузу и острый угол
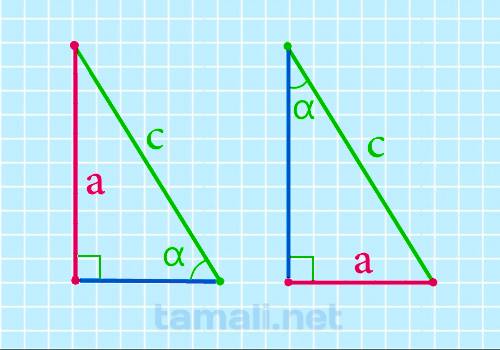
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:
a = c * sin α
где c — гипотенуза, α — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее: a = 77 * 0,98 = 75,8см.
Катет прямоугольного треугольника через гипотенузу и другой известный катет
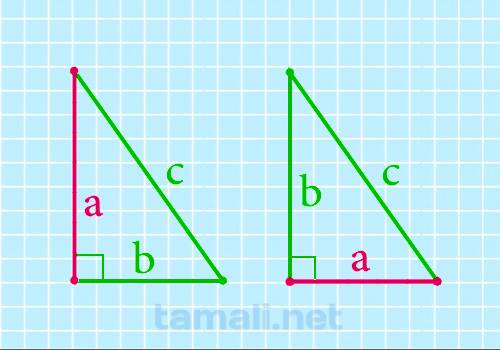
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:
a = √(c² — b²)
где c — гипотенуза, b — катет который известен прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см
Гипотенуза прямоугольного треугольника через катет и острый угол
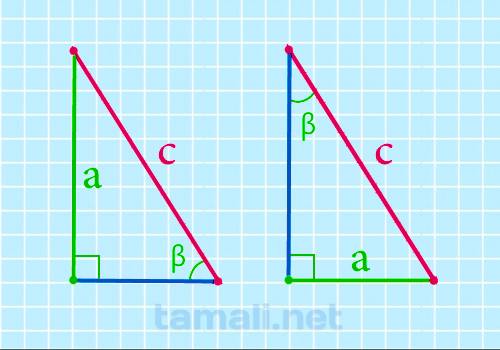
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:
c = a / sin(β)
где a — катет, β — острый угол прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.
Гипотенуза прямоугольного треугольника через катеты
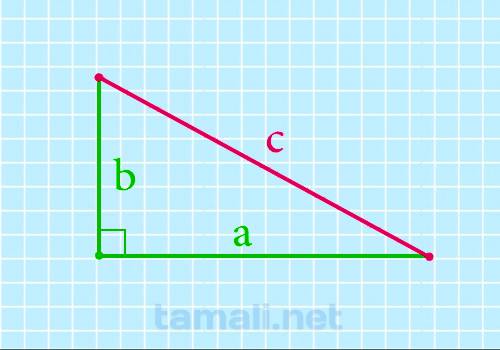
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:
c = √(a² + b²)
где c — гипотенуза, a и b — катеты.
Цифр после
запятой:
Результат в:
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см
Сторона треугольника через две известные стороны и угол между ними
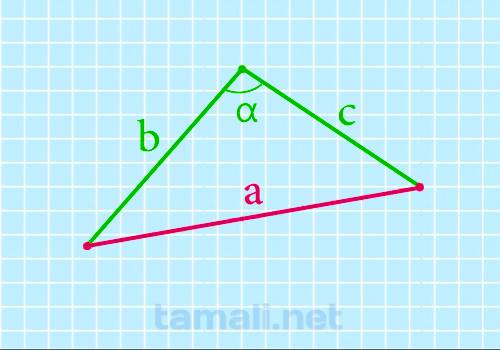
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:
a = b² + c² — 2bc * cos α
где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.
Цифр после
запятой:
Результат в:
Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.
Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.
Сторона треугольника через известную сторону и два угла
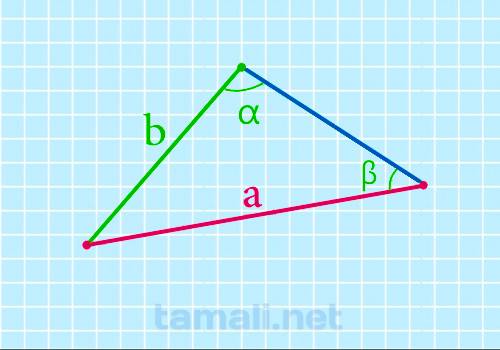
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:
a = (b * sin α) / sin β
где b — сторона треугольника; β, α — углы треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть сторона треугольника b равна 10, угол β = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30 = 8.71723 мм.























