Как найти боковые ребра прямоугольной пирамиды
Пирамида — это геометрическое тело с многоугольником в основании и боковыми треугольными гранями с общей вершиной. Количество боковых граней пирамиды равно числу сторон основания.
В прямоугольной пирамиде одно из боковых ребер перпендикулярно плоскости основания. Это ребро одновременно является высотой многогранника. Две боковые стороны, к плоскостям которых принадлежит совпадающее с высотой ребро, являются прямоугольными треугольниками.
Рассмотрите прямоугольный треугольник, представляющий боковую грань прямоугольной пирамиды. Его катеты — высота пирамиды и одна из сторон основания, гипотенуза — неизвестное боковое ребро многогранника. Вычислить неизвестную величину можно по теореме Пифагора. Боковое ребро пирамиды определится, как корень квадратный из суммы квадратов высоты тела и стороны основания.
В прямоугольной пирамиде две боковых грани в форме прямоугольного треугольника. Рассмотрите второй прямоугольный треугольник. Два треугольника имеют один общий катет, равный высоте пирамиды. Для нахождения еще одного бокового ребра вычислите гипотенузу второго прямоугольного треугольника.
Если в основании прямоугольной пирамиды лежит треугольник, то задача нахождения боковых ребер тела решена. В случае произвольного многоугольника в основании задача может быть решена двумя способами. Начиная с боковых граней в форме прямоугольных треугольников последовательно рассматривать остальные боковые грани, определяя неизвестное боковое ребро как третью сторону треугольника по двум известным.
Другим способом найти боковые ребра прямоугольной пирамиды можно последовательным нахождением гипотенузы прямоугольного треугольника, в котором катетами являются высота пирамиды и отрезок, проведенный в основании от начала высоты к основанию искомого ребра.
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр — боковое ребро пирамиды.
Пирамида как фигура геометрии
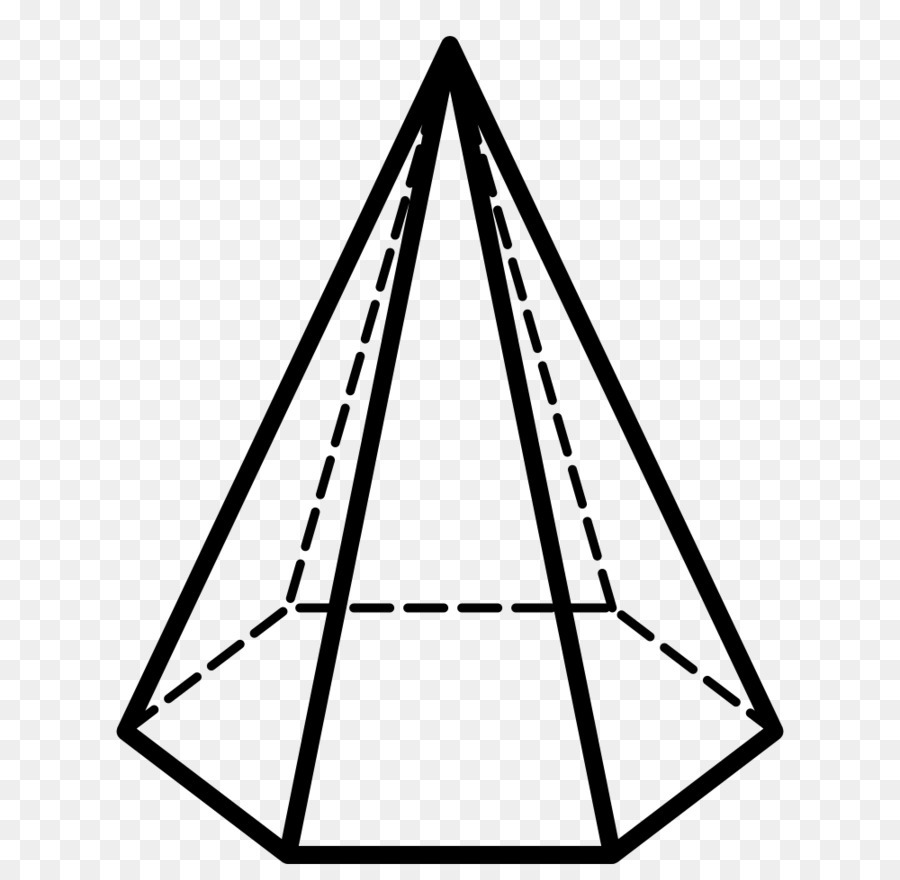
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
- гранями;
- ребрами;
- вершинами.
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника — с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид — это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса
Каждый человек знает, что первое чудо света — пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса — треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней — это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Где высота правильной треугольной пирамиды равна h, а ее сторона основания — a.
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
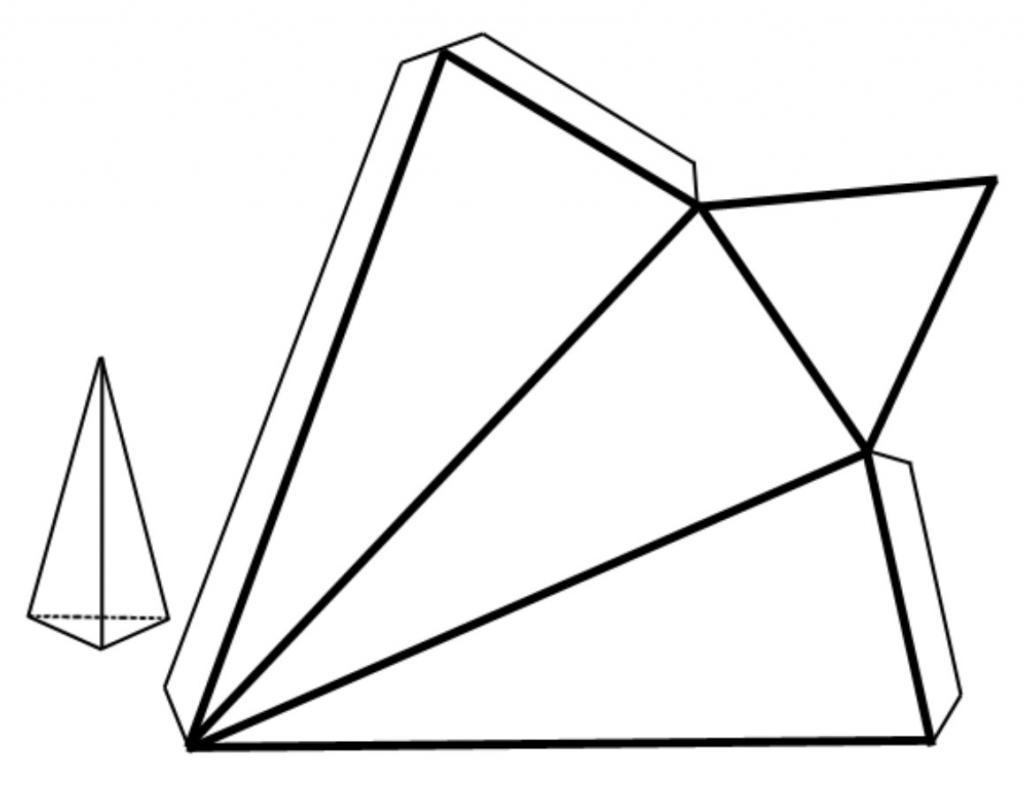
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Здесь первое слагаемое — это площадь боковой поверхности, второе слагаемое — площадь треугольных оснований.
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Геометрические фигуры. Правильная пирамида.
Правильная пирамида — когда основанием пирамиды является правильный многоугольник, а высота проецируется в центр основания (или проходит через него).
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.
Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
V — объем пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды,
Sb — площадь боковой поверхности пирамиды,
a — апофема (не путать с α) пирамиды,
P — периметр основания пирамиды,
n — число сторон основания пирамиды,
b — длина бокового ребра пирамиды,
α — плоский угол при вершине пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
V — объем правильной пирамиды,
h — высота правильной пирамиды,
n — количество сторон правильного многоугольника, основания правильной пирамиды,
a — длина стороны правильного многоугольника.
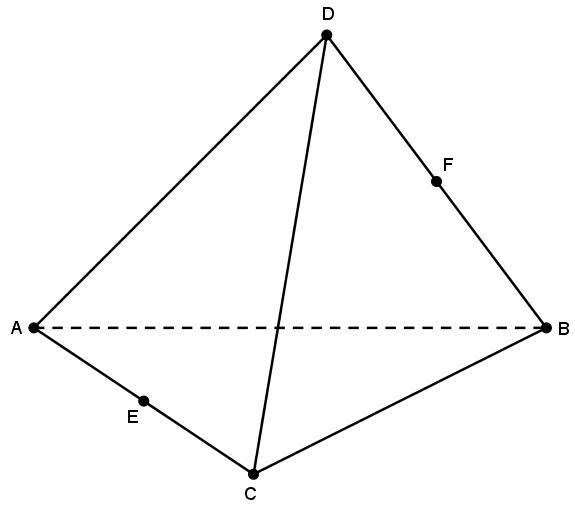
Боковое ребро правильной пирамиды находят по формуле:
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) — основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида — это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
V — объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h — высота правильной пирамиды,
a — длина стороны основания правильной пирамиды.
Так как правильная треугольная пирамида — это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
http://1ku.ru/obrazovanie/41519-formuly-i-svojstva-pravilnoj-treugolnoj-piramidy-usechennaja-treugolnaja-piramida/
http://www.calc.ru/Geometricheskiye-Figury-Pravilnaya-Piramida.html
Правильная пирамида – это геометрическое тело, образованное правильным многоугольником, лежащим в основании и боковыми ребрами, подымающимися в одну вершину из всех углов основания. Такая пирамида является типовой, поскольку обладает множеством свойств за счет своего основания. Помимо того, что все боковые грани представляют собой конгруэнтные треугольники, а все боковые ребра равны (также как и ребра в основании между собой), высота правильной пирамиды опускается ровно в центр вписанной и описанной окружностей для заданного многоугольника. Поэтому в такой пирамиде возникает сразу два прямоугольных треугольника во внутреннем пространстве, один из них соединяет высоту с апофемой радиусом вписанной окружности, а второй соединяет высоту с боковым ребром радиусом описанной окружности.
Таким образом, для того, чтобы найти боковое ребро пирамиды, необходимо знать лишь сторону основания, общее количество сторон этого же многоугольника и высоту. По теореме Пифагора, боковое ребро является гипотенузой и, следовательно, находится сложением:
Подставив в формулу значение радиуса описанной окружности для правильного многоугольника, получаем окончательный ее вид:
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по теме «Правильная и прямоугольная пирамиды»
(blacktriangleright) Пирамида называется прямоугольной, если одно из ее боковых ребер ((SR)) перпендикулярно основанию (оно же будет и высотой).
Грани, образованные этим ребром, будут представлять собой прямоугольные треугольники ((triangle SMR, triangle SPR)).
(blacktriangleright) Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:
(sim) боковые ребра равны;
(sim) высота пирамиды проходит через центр описанной около основания окружности;
(sim) боковые ребра наклонены к основанию под одинаковым углом.
(blacktriangleright) Заметим, что у правильных многоугольников центры описанной и вписанной окружностей совпадают.
(blacktriangleright) Заметим, что у правильной пирамиды все боковые грани – равные равнобедренные треугольники.
Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой.
Задание
1
#2854
Уровень задания: Равен ЕГЭ
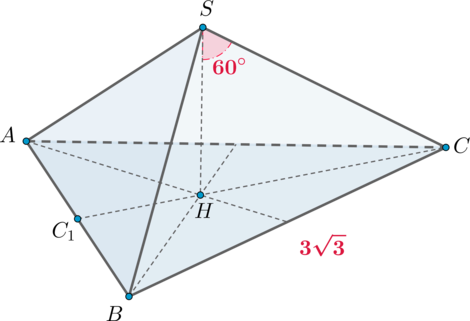
Дана правильная треугольная пирамида (SABC) с вершиной (S). Известно, что сторона основания пирамиды равна (3sqrt3), а угол между ее высотой и боковым ребром равен (60^circ). Найдите объем пирамиды.
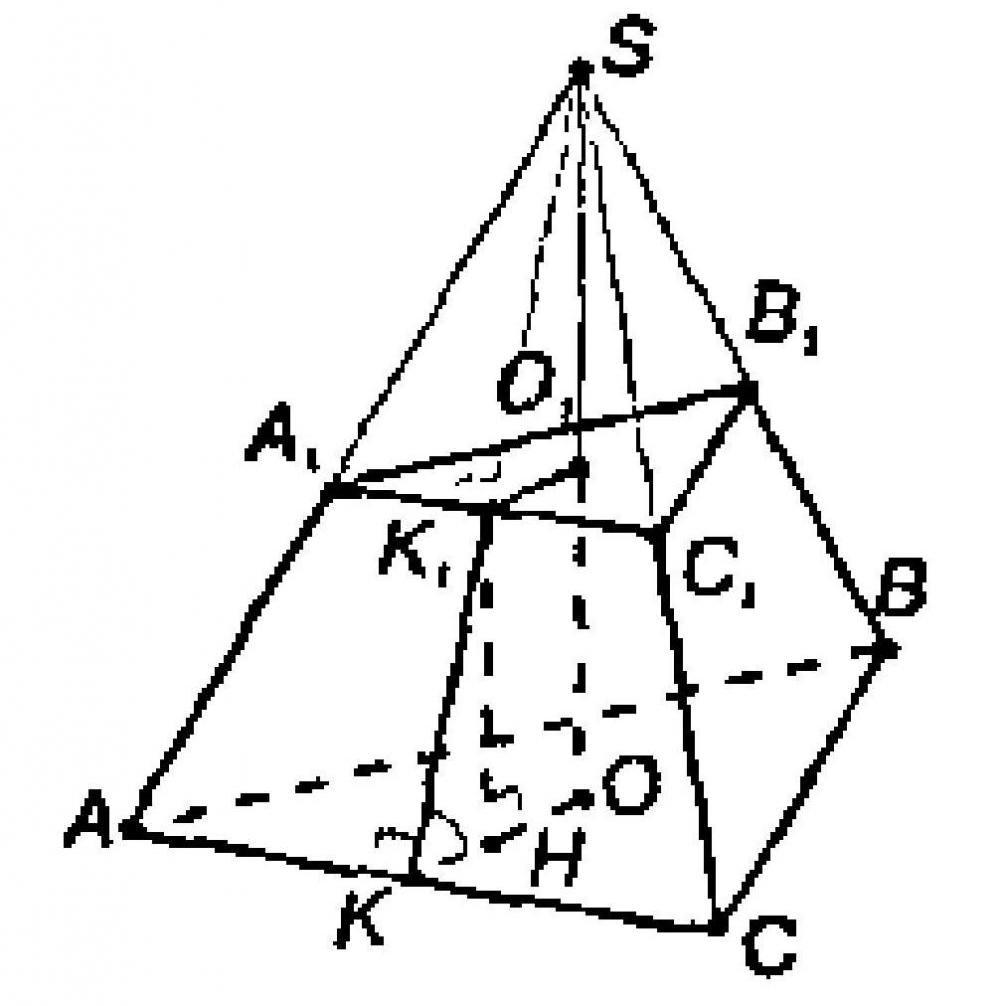
Пусть (SH) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис).
Пусть (CC_1) – высота (а значит и медиана) основания. Тогда [CC_1=dfrac{sqrt3}2AB.] Так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [CH=dfrac23CC_1=dfrac{sqrt3}3AB.] Из прямоугольного (triangle SHC): [mathrm{tg},60^circ=dfrac{CH}{SH}quadRightarrowquad
SH=dfrac{CH}{sqrt3}=dfrac13AB.] Следовательно, объем пирамиды равен [V=dfrac13cdot SHcdot S_{ABC}=dfrac13cdot
dfrac13cdot 3sqrt3cdot dfrac12cdot 3sqrt3cdot
dfrac{sqrt3}2cdot 3sqrt3=dfrac{27}4=6,75.]
Ответ: 6,75
Задание
2
#2856
Уровень задания: Равен ЕГЭ
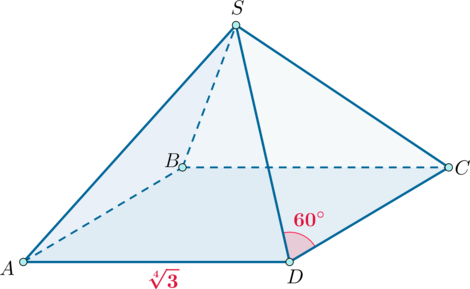
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S). Угол между боковым ребром и стороной основания равен (60^circ), а (AB=sqrt[4]3). Найдите площадь боковой поверхности этой пирамиды.
Так как пирамида правильная, то все боковые грани представляют собой равные равнобедренные треугольники. Так как у них угол при основании равен (60^circ), то они являются равносторонними, то есть все боковые ребра пирамиды равны стороне основания. Площадь правильного треугольника со стороной (a) вычисляется по формуле (dfrac{sqrt3}4a^2), следовательно, площадь боковой поверхности [S_{text{бок. пов-ти}}=4cdot dfrac{sqrt3}4AS^2=sqrt3AS^2=sqrt3cdot sqrt3=3.]
Ответ: 3
Задание
3
#2858
Уровень задания: Равен ЕГЭ
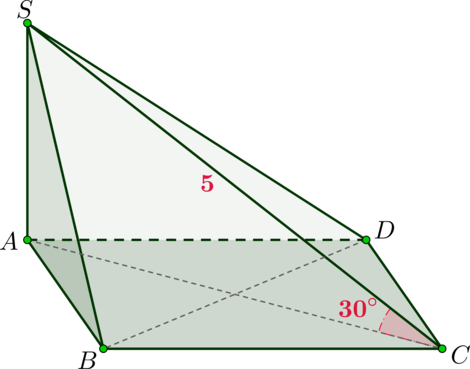
Дана прямоугольная пирамида (SABCD), причем (SA) – высота пирамиды, а (ABCD) – ромб. Диагональ (BD) ромба равна (8sqrt3), а боковое ребро (SC) равно (5). Найдите объем пирамиды, если также известно, что угол между (SC) и плоскостью основания равен (30^circ).
Так как (SA) – высота, то она перпендикулярна плоскости основания, следовательно, по определению (AC) является проекций (SC) на плоскость основания. А так как угол между прямой и плоскостью – это угол между прямой и ее проекцией на плоскость, то (angle SCA) – угол между (SC) и основанием.
Так как (SA) перпендикулярна основанию, то она перпендикулярна любой прямой из основания, следовательно, (triangle SAC) прямоугольный. Значит, (AS) как катет, лежащий против угла (30^circ), равен половине (SC), то есть (AS=2,5).
По теореме Пифагора из этого же треугольника [AC=sqrt{SC^2-SA^2}=2,5sqrt3.] Так как площадь ромба равна полупроизведению диагоналей, то объем [V=dfrac13cdot SAcdot dfrac12cdot ACcdot BD=25.]
Ответ: 25
Задание
4
#1865
Уровень задания: Равен ЕГЭ
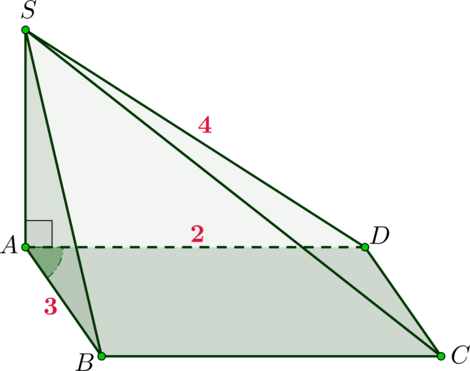
В прямоугольной пирамиде (SABCD): (SB) – высота пирамиды, (ABCD) – прямоугольная трапеция с прямыми углами (angle BAD) и (angle ABC). Найдите объем пирамиды, если (angle SAB = 60^circ), (angle SCB = 30^circ), (AD = 2cdot AB), а (AB = sqrt3).
(triangle ABS) и (triangle CBS) – прямоугольные треугольники (Rightarrow) (SB = ABcdotmathrm{tg},60^circ = sqrt3cdotsqrt3 = 3) (Rightarrow) (BC = SBcdot mathrm{ctg},30^circ = 3sqrt3) (Rightarrow) (S_{ABCD} = frac{1}{2}cdot(AD + BC)cdot AB = frac{1}{2}cdot(2sqrt3 + 3sqrt3)cdotsqrt3 = 7,5) (Rightarrow) [V_{text{пир.}} = frac{1}{3}cdot SBcdot S_{ABCD} = frac{1}{3}cdot3cdot7,5 = 7,5]
Ответ: 7,5
Задание
5
#3113
Уровень задания: Равен ЕГЭ
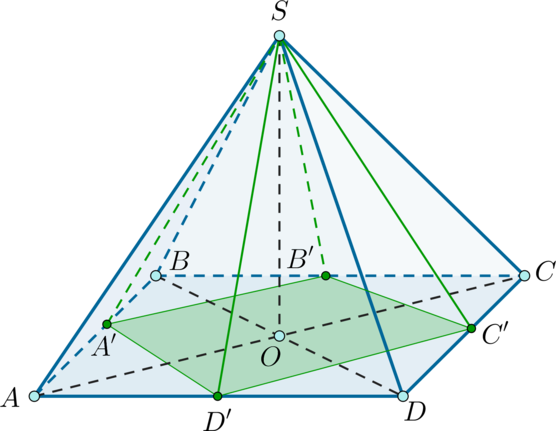
Дана правильная четырехугольная пирамида, объем которой равен (7). Найдите объем пирамиды, вершина которой совпадает с вершиной исходной пирамиды, а вершины основания совпадают с серединами сторон основания исходной пирамиды.
Рассмотрим рисунок. Пусть (SABCD) – исходная пирамида, (A’, B’, C’,
D’) – середины отрезков (AB, BC, CD, DA) соответственно. (SO) – высота пирамиды (SABCD). [V_{SABCD}=dfrac13cdot SOcdot AB^2] Заметим, что (SO) – также высота пирамиды (SA’B’C’D’).
Так как (ABC) – прямоугольный треугольник, то (AC=sqrt{AB^2+BC^2}=sqrt2AB). Так как (A’B’) – средняя линия в (triangle ABC), то [A’B’=frac12AC=dfrac{sqrt2}2AB] Так как (A’B’parallel AC, A’D’parallel BD), а (ACperp BD), то (A’B’perp
A’D’), следовательно, (A’B’C’D’) – квадрат. Следовательно, [V_{SA’B’C’D’}=dfrac13cdot SOcdot A’B’^2=dfrac13cdot SOcdot
dfrac12AB^2=
dfrac12V_{SABCD}=3,5.]
Ответ: 3,5
Задание
6
#2857
Уровень задания: Сложнее ЕГЭ
Дана прямоугольная пирамида (SABCD), в основании которой лежит параллелограмм со сторонами (AD) и (AB), соответственно равными (2) и (3), и углом между ними (arcsin dfrac{sqrt3}4), а боковое ребро (SA) перпендикулярно основанию. Найдите объем пирамиды, если (SD=4).
Пусть (angle DAB=arcsin dfrac{sqrt3}4), следовательно, (sinangle DAB=dfrac{sqrt3}4).
Так как (SA) перпендикулярно основанию, то оно перпендикулярно любой прямой из основания, следовательно, (triangle SAD) – прямоугольный. Также по определению (SA) является высотой пирамиды. Следовательно, по теореме Пифагора [SA=sqrt{SD^2-AD^2}=2sqrt3.] Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними, следовательно, объем пирамиды равен [V=dfrac13cdot SAcdot ABcdot ADcdot sinangle DAB=3.]
Ответ: 3
Задание
7
#2853
Уровень задания: Сложнее ЕГЭ
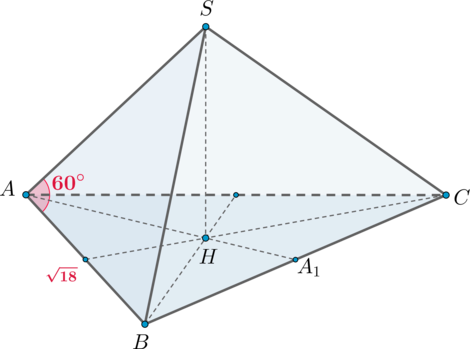
Дана правильная треугольная пирамида (SABC) с основанием (ABC), сторона которого равна (sqrt{18}). Найдите объем пирамиды, если угол (SAB) равен (60^circ).
Пусть (SH) – высота пирамиды. Так как пирамида правильная, то высота падает в центр основания, то есть в точку пересечения медиан (высот, биссектрис). Также боковые грани представляют собой равнобедренные треугольники. Так как в равнобедренном (triangle
ASB) угол при основании равен (60^circ), то треугольник равносторонний, следовательно, (AS=AB=sqrt{18}).
Пусть (AA_1) – высота основания. Следовательно, [AA_1=dfrac{sqrt3}2AB.] Так как (AA_1) – медиана, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то [AH=dfrac23AA_1=dfrac{sqrt3}3AB.] Следовательно, по теореме Пифагора [SH=sqrt{AS^2-AH^2}=dfrac{sqrt6}3AB.] Тогда объем пирамиды равен [V=dfrac13cdot SHcdot S_{ABC}=
dfrac13cdot dfrac{sqrt6}3ABcdot dfrac12cdot ABcdot dfrac{sqrt3}2AB=9.]
Ответ: 9
Задания из раздела «Геометрия в пространстве» по теме «Правильная и прямоугольная пирамида» являются обязательной частью ЕГЭ по математике. Понимать, как найти правильный ответ, и оперативно справляться с ними должны учащиеся с различным уровнем подготовки. Школьники, которые знают принцип решения задач с правильной треугольной и четырехугольной пирамидой, смогут выполнять задания с любым количеством действий и рассчитывать на получение достойных баллов по итогам сдачи аттестационного испытания.
Выбирайте образовательный портал «Школково» для успешной сдачи единого государственного экзамена!
Часто во время подготовки к аттестационному испытанию учащиеся сталкиваются с проблемой поиска подходящего источника. Школьный учебник далеко не всегда присутствует под рукой, когда это необходимо. А поиск требуемых формул для вычисления, к примеру, объема прямоугольной пирамиды, бывает достаточно сложным даже в Интернете в онлайн-режиме.
Для того чтобы подобные задания не вызывали затруднений, готовьтесь к единому государственному экзамену вместе с математическим порталом «Школково». Мы предлагаем принципиально новый подход к построению занятий с выпускниками. Наш портал помогает учащимся выявить наиболее сложные разделы и улучшить собственные знания.
Что такое правильная и прямоугольная пирамида, как вычисляются объем и площадь пирамиды, какие базовые теоремы и важные нюансы нужно знать для выполнения заданий — всю эту информацию вы найдете в разделе «Теоретическая справка». Этот материал систематизирован и изложен нашими специалистами с учетом их богатого опыта максимально просто и понятно.
Чтобы задачи ЕГЭ на площадь поверхности правильной пирамиды не вызывали особых сложностей, мы предлагаем также попрактиковаться в выполнении соответствующих упражнений. Найти подобные задания вы можете в разделе «Каталог».

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Содержание статьи:
- Пирамида как фигура геометрии
- Элементы пирамиды
- Правильные пирамиды
- Треугольная пирамида
- Четырехугольная пирамида
- Задача на определение бокового ребра пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр — боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.

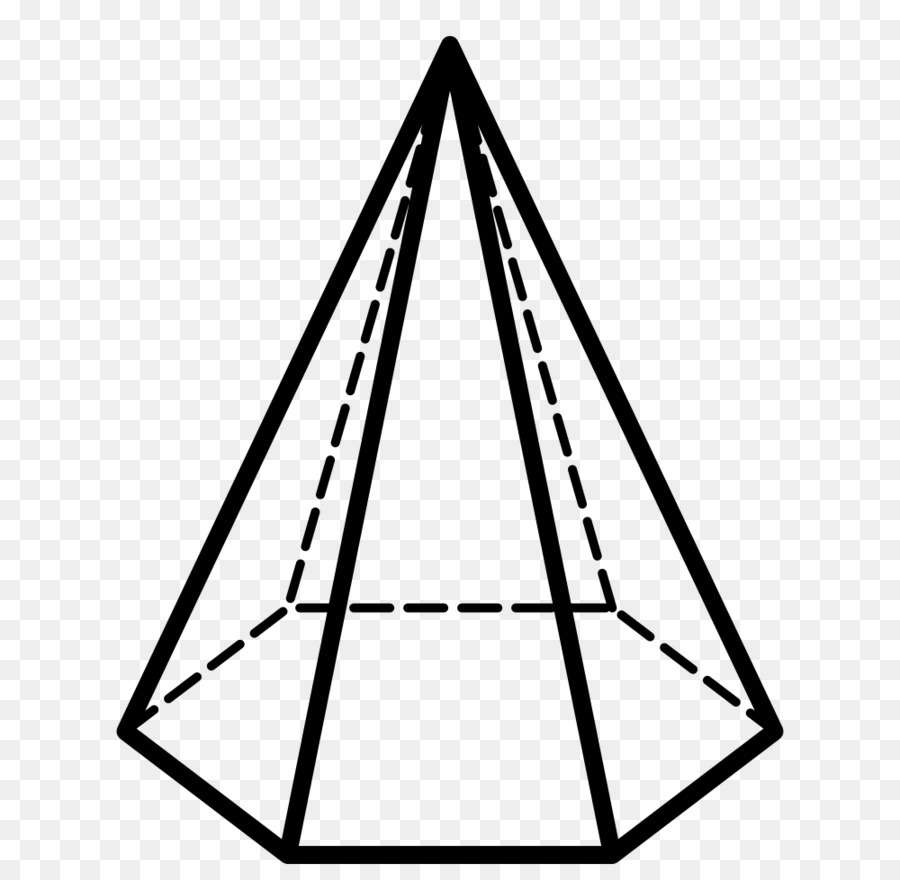
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
- гранями;
- ребрами;
- вершинами.
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника — с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
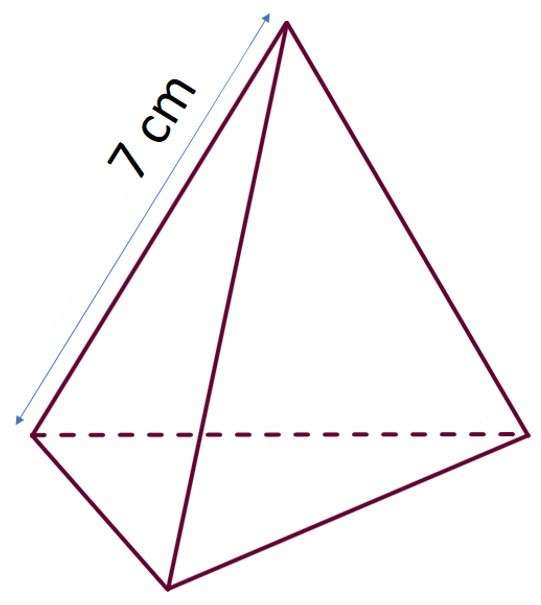
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
b = √(hb2 + a2/4);
b = √(h2 + a2/3).
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
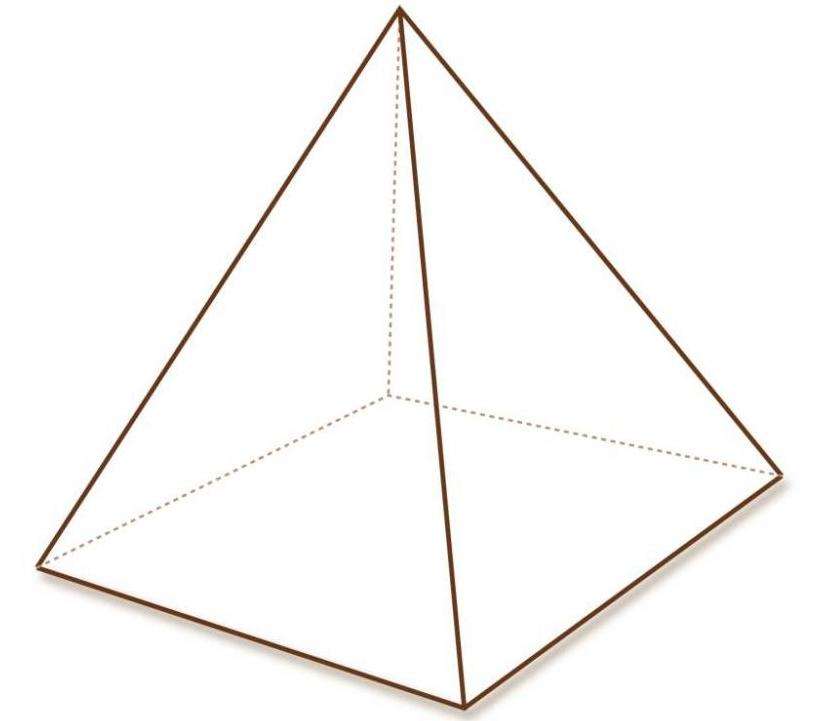
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
b = √(hb2 + a2/4);
b = √(h2 + a2/2).
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид — это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса

Каждый человек знает, что первое чудо света — пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
b = √(h2 + a2/2).
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).