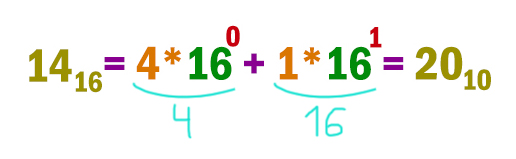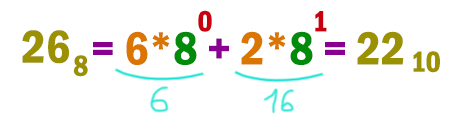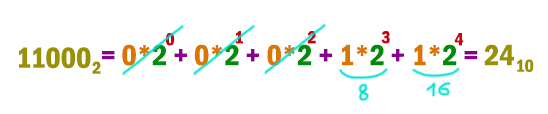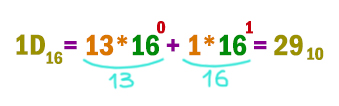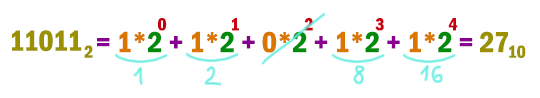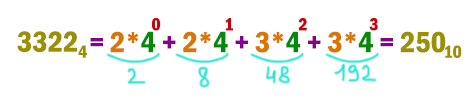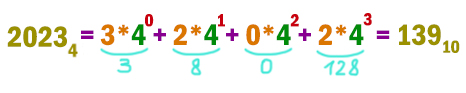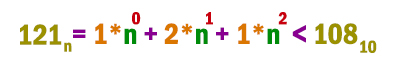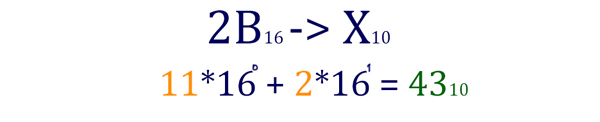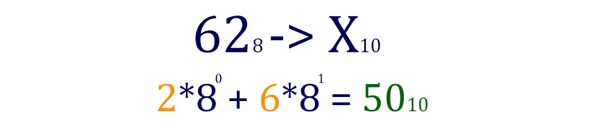Как найти большее число в системе счисления

Привет! Сегодня исследуем 10 Задание из ОГЭ по информатике 2023.

Задание 9 из ОГЭ по информатике Вы можете научиться решать, прочитав статью по 13 заданию из ЕГЭ по информатике. Эту статью Вы можете найти здесь.

Десятое задание проверяет умение работать с различными системами счисления.

Задача (Классическая)

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение:

Число 14 находится в шестнадцатеричной системе. Об этом говорит маленький индекс возле числа. Переведём его в нашу родную десятичную систему.

Берём поочередно цифры, начиная с младшего разряда. Первую правую цифру умножаем на 16 в нулевой степени, вторую цифру на 16 в первой степени и т.д. Умножаем на 16, потому что переводим из шестнадцатеричной системы. Степень потихоньку увеличивается на 1.

Необходимо помнить, что любое число в нулевой степени это единица!

Остаётся только посчитать полученный пример. Получается число 20 в десятичной системе.

Переведём число 26₈ из восьмеричной системы в нашу родную десятичную систему. Делаем аналогично предыдущему примеру.

Аналогично переведём число и из двоичной системы.

Наибольшее из трёх чисел это 24.

Ответ: 24

Задача (Классическая, закрепление)

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

1D₁₆, 36₈, 11011₂

Решение:

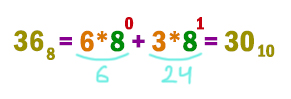
В шестнадцатеричной системе буквы при переводе в десятичную систему нужно превратить в числа.

A	B	C	D	E	F
10	11	12	13	14	15

Переведём первое число.

Переведём второе число.

Переведём третье число.

Наибольшее число получается 30.

Ответ: 30

Задача (Из десятичной в двоичную)

Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

59₁₀, 71₁₀, 81₁₀

Решение:

Нужно каждое число перевести в двоичную систему счисления.

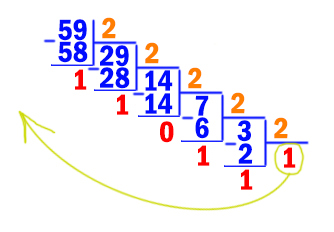
Переведём число 59₁₀ в двоичную систему.

Получается 59₁₀ = 111011₂. Здесь мы делим уголком на 2 (на основание системы, куда переводим) с остатком. Продолжаем делить, пока не получим 1. Затем остатки записываем задом наперёд. Получается число в двоичной системе счисления. Последнее число 1 (единицу) тоже берём.

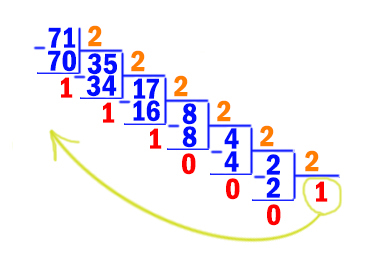
Переведём число 71₁₀ в двоичную систему.

Получается 71₁₀ = 1000111₂.

Переведём число 81₁₀ в двоичную систему.

Получается 81₁₀ = 1010001₂.

Найдём количество единиц для каждого числа, записанного в двоичной системе.

111011₂, Кол. ед.: 5
1000111₂, Кол ед.: 4
1010001₂, Кол ед.: 3

Ответ: 3

Задача (Из десятичной в восьмеричную)

Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, сумма цифр которого в восьмеричной записи наименьшая. В ответе запишите сумму цифр в восьмеричной записи этого числа.

86₁₀, 99₁₀, 105₁₀

Решение:

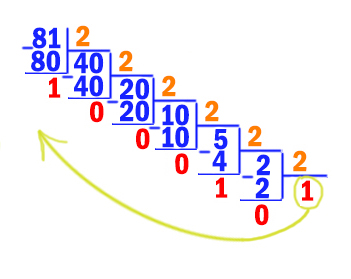
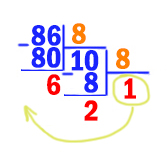
Переведём число 86₁₀ в восьмеричную систему.

Делаем аналогично тому, как мы переводили в двоичную систему, только теперь уголком делим на 8. Остатки могут получатся от 0 до 7.

Как только в результате деления получили число меньшее, чем 8, то завершаем процесс перевода.

Остатки опять записываем задом наперёд. Последнее число тоже участвует в формировании результата наравне с остатками.

Получается 86₁₀ = 126₈.

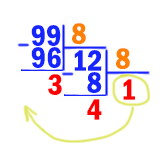
Переведём число 99₁₀ в восьмеричную систему.

Получается 99₁₀ = 143₈.

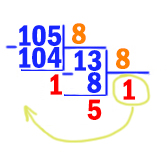
Переведём число 105₁₀ в восьмеричную систему.

Получается 105₁₀ = 151₈.

Найдём сумму цифр у полученных чисел.

126₈, Сумма цифр: 9
143₈, Сумма цифр: 8
151₈, Сумма цифр: 7

Наименьшая сумма цифр равна 7.

Ответ: 7

Разберём несколько нестандартных тренировочных задач для подготовки к 10 заданию ОГЭ по информатике.

Задача(Неожиданная)

Число 3322_n записано в системе счисления с основанием n (n > 1). Определите наименьшее возможное значение n. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Наименьшее значение n в этой задаче может быть равно 4, потому что самая большая цифра — это тройка. Мы берём на 1 больше, т.к. в четверичной системе могут применяться только цифры: 0, 1, 2, 3. Тоже самое, как в нашей родной десятичной системе могут применяться 10 цифр: от нуля, до девяти. Самая большая цифра в нашей родной десятичной системе девятка.

Осталось перевести данное число из четверичной системы в десятичную.

Ответ: 250

Задача (Уже знаем)

Число 2023_n записано в системе счисления с основанием n (n > 1). Определите значение n, при котором данное число минимально. Для этого значения n в ответе запишите представление данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Здесь нужно, чтобы само число 2023_n было минимальным. Но это число будет минимальным, если мы выберем самое маленькое значение n при данных цифрах.

Самое маленькое основание системы может вновь 4. Переведём наше число 2023₄ из четверичной системы в десятичную.

Получается число 139.

Ответ: 139

Задача (Крепкий орешек)

Число 121_n записано в системе счисления с основанием n (n > 1). Определите наибольшее возможное значение n, для которого 121_n < 108₁₀. Для этого значения n в ответе запишите представления данного числа в десятичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

Мы не знаем в какой системе счисления записано число. Но всё равно начнём переводить его в десятичную систему, оставив переменную n в виде неизвестной.

Попробуем подобрать n.

При n=10

1*10⁰ + 2*10¹ + 1*10² = 121 > 108₁₀

Перебор. Ну это и так было понятно.

Значит, нужно уменьшать n. Возьмём n = 9.

1*9⁰ + 2*9¹ + 1*9² = 100 < 108₁₀

Как раз получилось число, которое меньше числа 108₁₀. Это и есть наибольшее n!

В ответе просили перевести исходное число в десятичную систему. Это и есть число 100, уже всё переведено.

Ответ: 100

Задача (Не все цифры одинаковые)

Десятичное число 511 записано в системе счисления с основанием n (n > 1). Определите минимальное значение n, при котором в полученной записи числа не все цифры одинаковые. В ответе запишите запись числа в системе счисления с найденным основанием n. Основание системы счисления указывать не нужно.

Решение:

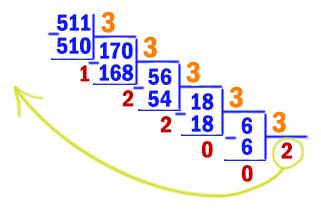
Начнём перебирать основание системы n, начиная с наименьшего значения 2. Переведём число 511₁₀ в двоичную систему.

Можно переводить стандартно, через деление уголком на 2. Но в данном случае видно, что число 511 близко к 512. Число 512 = 2⁹.

Существует правило:

2⁴ = 10000₂
2⁶ = 1000000₂

Т.е. степень двойки показывает, сколько после единицы нулей у числа в двоичной системе.

Это касается любой системы счисления.

3² = 100₃
3³ = 1000₃

Наше число

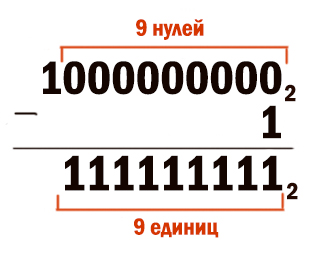
511₁₀ = 512₁₀ — 1 = 2⁹ — 1 = 1000000000₂ — 1

Сделаем вычитание столбиком.

Вычитание или суммирование столбиком в любой системе счисления выполняются так же, как и в нашей системе счисления. Здесь мы вычитаем единицу из нуля. Ноль идёт занимать у более старшего разряда и т.д. В итоге обращаемся к самой старшей единице. Эта единица превращается в младшем разряде в двойку, потому что работаем в двоичной системе. Как и в нашей системе, когда занимаем у старшего разряда единицу, она превращается в десяток. В итоге каждая двойка отдаёт единицу в младший разряд. В самом младшем разряде получается действие 2-1=1. А все разряды, т.к. отдали единицу в младший разряд превратятся в 1.

Получается 511₁₀ = 200221₃.

Видим, что не все цифры у числа одинаковые в троичной системе. И число n = 3 — это минимально возможное число.

Ответ: 200221

Задача(Диапазон чисел)

Сколько существует целых чисел x, для которых выполняется неравенство

2B₁₆ < x < 62₈?

В ответе укажите только количество чисел, сами числа писать не нужно.

Решение:

Нам нужно узнать сколько чисел находятся в диапазоне от 2B₁₆ до 62₈.
Переведём числа 2B₁₆ и 62₈ в нашу родную десятичную систему счисления. Затем, мы уже сможем сообразить, сколько чисел вмещается в этот диапазон.

Чтобы перевести число из любой системы счисления в нашу родную десятичную, необходимо воспользоваться методом «возведения в степень».

Начинаем с младшего разряда. Цифра «B» превращается в 11. 2B₁₆ = 43₁₀. Теперь переведём число
62₈ в десятичную систему.

Таким образом, наше неравенство принимает вид 43 < x < 50. Кажется, что нужно сделать 50 — 43 = 7. Но если мы подставим небольшие числа 4 < x < 6, то мы увидим, что метод 6-4=2 неверен. Число будет только одно: 5 (пять). Поэтому и от нашего числа 7 мы тоже должны отнять единицу. 7 — 1 = 6. И ответ будет 6.

Если бы у нас было в одном месте знак «больше или равно»: 2B₁₆ ≤ x < 62₈, то мы бы оставили число 7. А если было бы два знака «больше или равно», то даже прибавили единицу.

Ответ: 6

Сравнение чисел в различных системах счисления.

Системы счисление:

• Двоичная

• Восьмеричная

• Десятичная

• Шестнадцатеричная

Двоичные числа – каждая цифра обозначает значение одного бита (0 или 1), старший бит всегда пишется слева, индекс обозначает основание системы счисления. Например, .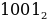

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7).

Десятичные числа – наиболее привычные для обычного человека в повседневной жизни (от 0 до 9). Обозначаются индексом 10. Например, .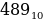

Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными. В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F.

Для того чтобы сравнить числа в различных системах счисления, необходимо выполнить перевод из различных систем счисления в десятичную.
Для перевода чисел в десятичную систему счисления выполняют развернутую запись исходного числа.

• Перевод из двоичной в десятичную.

В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:

5476 = 5000 + 400 + 70 + 6

Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:

5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100

После равенства числа 5, 4, 7 и 6 – это набор цифр, из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10. Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.

Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:

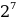
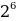
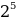
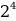
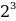
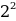
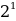
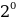
10001001 = 1 *  + 0 *  + 0 *  + 0 *  + 1 * + 0 * + 0 * + 1 *

Результат вычислений дает десятичное число, количественно равное двоичному 10001001:

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:

 =

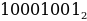
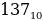
• Перевод из восьмеричной в двоичную.

Для преобразования двоичного числа в восьмеричное надо разбить его на тройки цифр и заменить каждую тройку соответствующей ей одной цифрой из восьмеричной системы счисления. Разбивать двоичное число на тройки следует с конца, а вместо недостающих цифр в начале можно записать нули.

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

В примере число 1011101 в двоичной системе приводится к числу 135 в восьмеричной системе счисления.

=

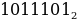
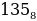
Как перевести восьмеричное число в десятичное? Здесь действует тот же алгоритм, как при преобразовании двоичного числа в десятичное. Однако в случае восьмеричного числа за основание степени берется десятичное число 8:

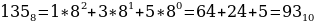
• Перевод из шестнадцатеричную в десятичную.

Перевод из шестнадцатеричной системы счисления в десятичную выполняется аналогично переводу из двоичной и восьмеричной. Только здесь в качестве основания степени выступает число 16, а цифры от A до F заменяются десятичными числами от 10 до 15.

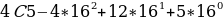
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи, – это число FF.

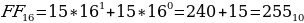
• Перевод из десятичной в двоичную

О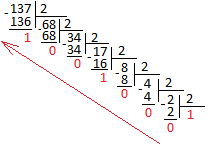 дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.

Получаем, что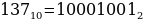

• Преобразование десятичного числа в восьмеричное также похоже на перевод в двоичное, за исключением того, что делить надо на 8

• Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же «алгоритм замещения», что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16

• Перевод двоичного в шестнадцатеричную

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.

Двоичное число	Шестнадцатеричное число
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Пример:

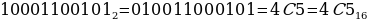
Теперь попробуем прорешать Задание №10 из ОГЭ

№ 10324

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

38₁₆, 75₈, 110100₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

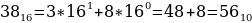
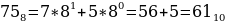
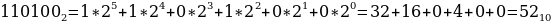
Таким образом, наибольшим среди этих трех чисел является чисто 61.

Ответ: 61.

 № 10325 

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

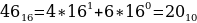
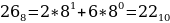
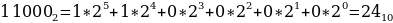
Таким образом, наибольшим среди этих трех чисел является чисто 24.

Ответ: 24.

№ 10329 

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

41₁₆, 77₈, 1000010₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

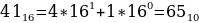
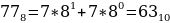
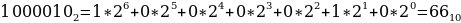
Таким образом, наименьшим среди этих трех чисел является чисто 63.

Ответ: 63.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале: