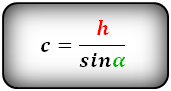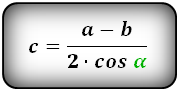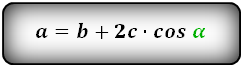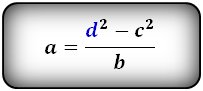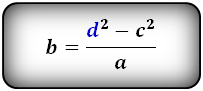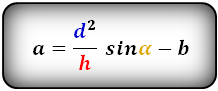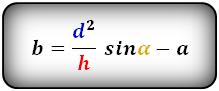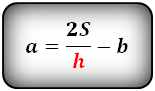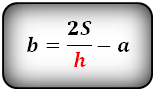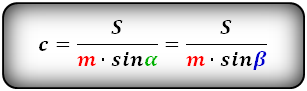Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Рассмотрим задачи:
27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Площадь трапеции (формула):
Нам известны основания и площадь, можем записать:
Ответ: 8
27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Формула площади при данных обозначениях вершин:
Нам известны основание, площадь и высота, можем записать:
Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.
27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Формула площади при данных обозначениях вершин:
Нам известны средняя линя и площадь, можем записать:
Ответ: 8
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:
Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:
Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):
По теореме Пифагора:
Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:
Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:
Таким образом площадь будет равна:
Ответ: 160
27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:
Теперь выполним дополнительные построения (опустим высоты):
Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:
Ответ: 5
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:
Высоту нашли, вычисляем площадь:
Ответ: 42
27593. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
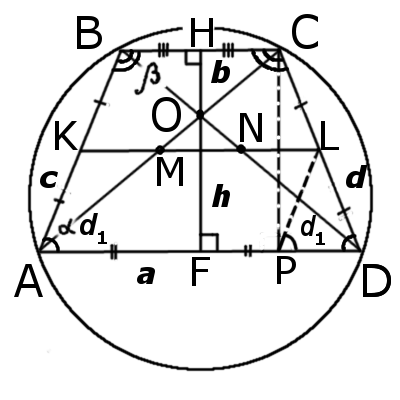 |
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
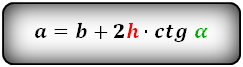
a = b + 2h ctg α = b + 2c cos α
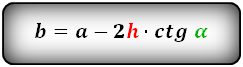
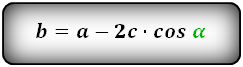
b = a — 2h ctg α = a — 2c cos α
| c = | h | = | a — b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 — c2 | b = | d12 — c2 | c = √d12 — ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a — h ctg α = b + h ctg α = a — √c2 — h2 = b + √c2 — h2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 — 2ac cos α
d1 = √b2 + c2 — 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию:
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 — (a — b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a — c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
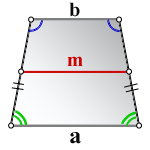
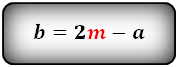
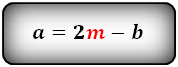
1. Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
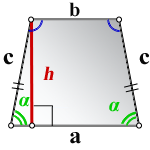
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
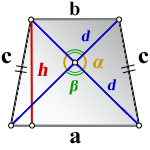
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
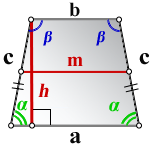
4. Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 08 октября 2013
-
Обновлено: 13 августа 2021
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.

Инструкция
Начертите равнобокую трапецию. Дана площадь трапеции — S, высота трапеции — h и боковая сторона — a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.

Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x — 2*n.
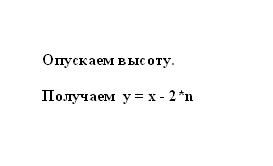
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² — h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
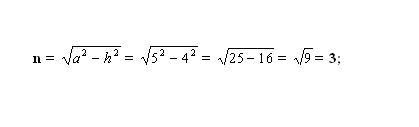
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
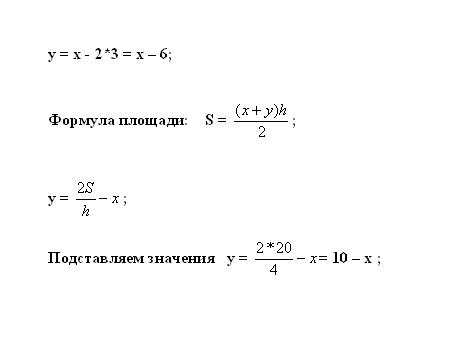
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y — меньшего основания.

Источники:
- высота равнобокой трапеции
Как найти основания трапеции
Основания трапеции можно найти несколькими способами, в зависимости от заданных параметров. При известной площади, высоте и боковой стороне равнобокой трапеции последовательность расчетов сводится к вычислениям стороны равнобедренного треугольника. А также к использованию свойства равнобокой трапеции.
Начертите равнобокую трапецию. Дана площадь трапеции — S, высота трапеции — h и боковая сторона — a. Опустите высоту трапеции на большее основание. Большее основание будет разделено на отрезки m и n.
Для определения длины обоих оснований (х, y) примените свойство равнобокой трапеции и формулу расчета площади трапеции.
Согласно свойству равнобокой трапеции отрезок n равен полуразности оснований х и y. Следовательно, меньшее основание трапеции y можно представить в виде разности большего основания и отрезка n, помноженного на два: y = x — 2*n.
Найдите неизвестный меньший отрезок n. Для этого вычислите одну их сторон получившегося прямоугольного треугольника. Треугольник образован высотой – h (катет), боковой стороной – a (гипотенуза) и отрезком – n (катет). Согласно теореме Пифагора неизвестный катет n² = a² — h². Подставьте известные числовые значения и высчитайте квадрат катета n. Возьмите корень квадратный из полученного значения – это и будет длина отрезка n.
Подставьте полученное значение в первое уравнение для вычисления y. Площадь трапеции высчитывается по формуле S = ((х + y)*h)/2. Выразите неизвестную переменную: y = 2*S/h – х.
Запишите оба полученных уравнения в систему. Подставляя известные значения, найдите две искомые величины в системе двух уравнений. Полученное решение системы х представляет собой длину большего основания, а y — меньшего основания.