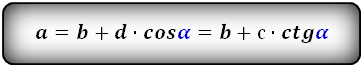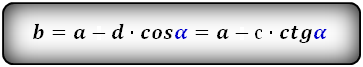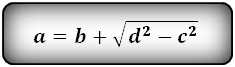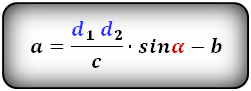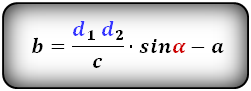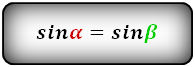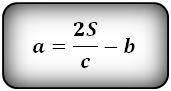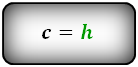Как найти основания прямоугольной трапеции
Математическая фигура с четырьмя углами называется трапецией, если пара противоположных ее сторон параллельна, а другая пара — нет. Параллельные стороны называют основаниями трапеции, две другие — боковыми. В прямоугольной трапеции один из углов при боковой стороне — прямой.
Инструкция
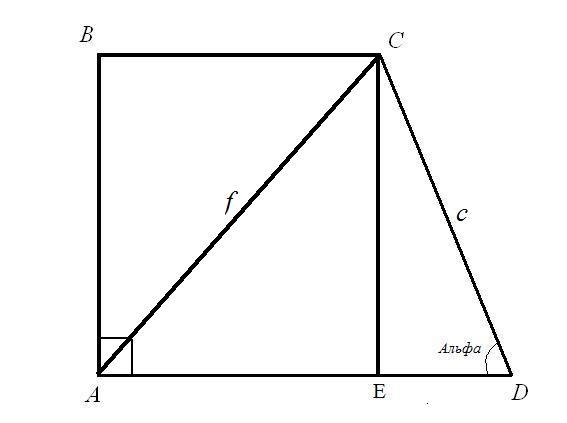
Задача 1.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали AC = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Известны гипотенуза c и угол между гипотенузой и катетом EDC. Найдите длины сторон CE и ED: по формуле угла CE = CD*sin(ADC); ED = CD*cos(ADC). Итак: CE = c*sinα; ED=c*cosα.
Рассмотрите прямоугольный треугольник ACE. Гипотенуза AC и катет CE вам известны, найдите сторону AE по правилу прямоугольного треугольника: сумма квадратов катетов равна квадрату гипотенузы. Итак: AE(2) = AC(2) — CE(2) = f(2) — c*sinα. Вычислите квадратный корень из правой части равенства. Вы нашли верхнее основание прямоугольной трапеции.
Длина основания AD является суммой длин двух отрезков AE и ED. AE = квадратный корень(f(2) — c*sinα); ED = c*cosα).Итак: AD = квадратный корень(f(2) — c*sinα) + c*cosα.Вы нашли нижнее основание прямоугольной трапеции.
Задача 2.Найдите основания BC и AD прямоугольной трапеции, если известна длина диагонали BD = f; длина боковой стороны CD = c и угол при ней ADC = α.Решение:Рассмотрите прямоугольный треугольник CED. Найдите длины сторон CE и ED: CE = CD*sin(ADC) = c*sinα; ED = CD*cos(ADC) = c*cosα.
Рассмотрите прямоугольник ABCE. По свойству прямоугольника AB = CE = c*sinα.Рассмотрите прямоугольный треугольник ABD. По свойству прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Поэтому AD(2) = BD(2) — AB(2) = f(2) — c*sinα.Вы нашли нижнее основание прямоугольной трапеции AD = квадратный корень(f(2) — c*sinα).
По правилу прямоугольника BC = AE = AD — ED = квадратный корень(f(2) — c*sinα) — с*cosα.Вы нашли верхнее основание прямоугольной трапеции.
Дано:
АВ (боковая сторона) — 30
СД (боковая сторона) — 50
ВС (меньшее основание) — 11
Найти: АД — ?
Решение:
Проведем дополнительное построение СН — высота. Так как трапеция прямоугольная, то мы имеем следующее: АВ = СН = 30 мм
Рассмотрим треугольник СНД, он прямоугольный так как СН — высота, проведенная перпендикулярно большего основания.
По теореме Пифагора найдем сторону НД.
НД^2 = СД^2 — СН^2
НД^2 = 2500 — 900
НД = 40 мм
АД = АН + АД
АН = ВС, так как трапеция прямоугольная и АВСН — прямоугольник, где параллельные основания равны.
Соответственно АД = 40 + 11
АД = 51
Ответ: 51 мм
Найти большее основание трапеции. Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Рассмотрим задачи:
27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Площадь трапеции (формула):
Нам известны основания и площадь, можем записать:
Ответ: 8
27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Формула площади при данных обозначениях вершин:
Нам известны основание, площадь и высота, можем записать:
Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.
27630. Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Формула площади при данных обозначениях вершин:
Нам известны средняя линя и площадь, можем записать:
Ответ: 8
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:
Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:
Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):
По теореме Пифагора:
Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Для вычисления площади нам необходимо найти высоту. Выполним дополнительные построения:
Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:
Таким образом площадь будет равна:
Ответ: 160
27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:
Теперь выполним дополнительные построения (опустим высоты):
Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:
Ответ: 5
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:
Высоту нашли, вычисляем площадь:
Ответ: 42
27593. Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
8
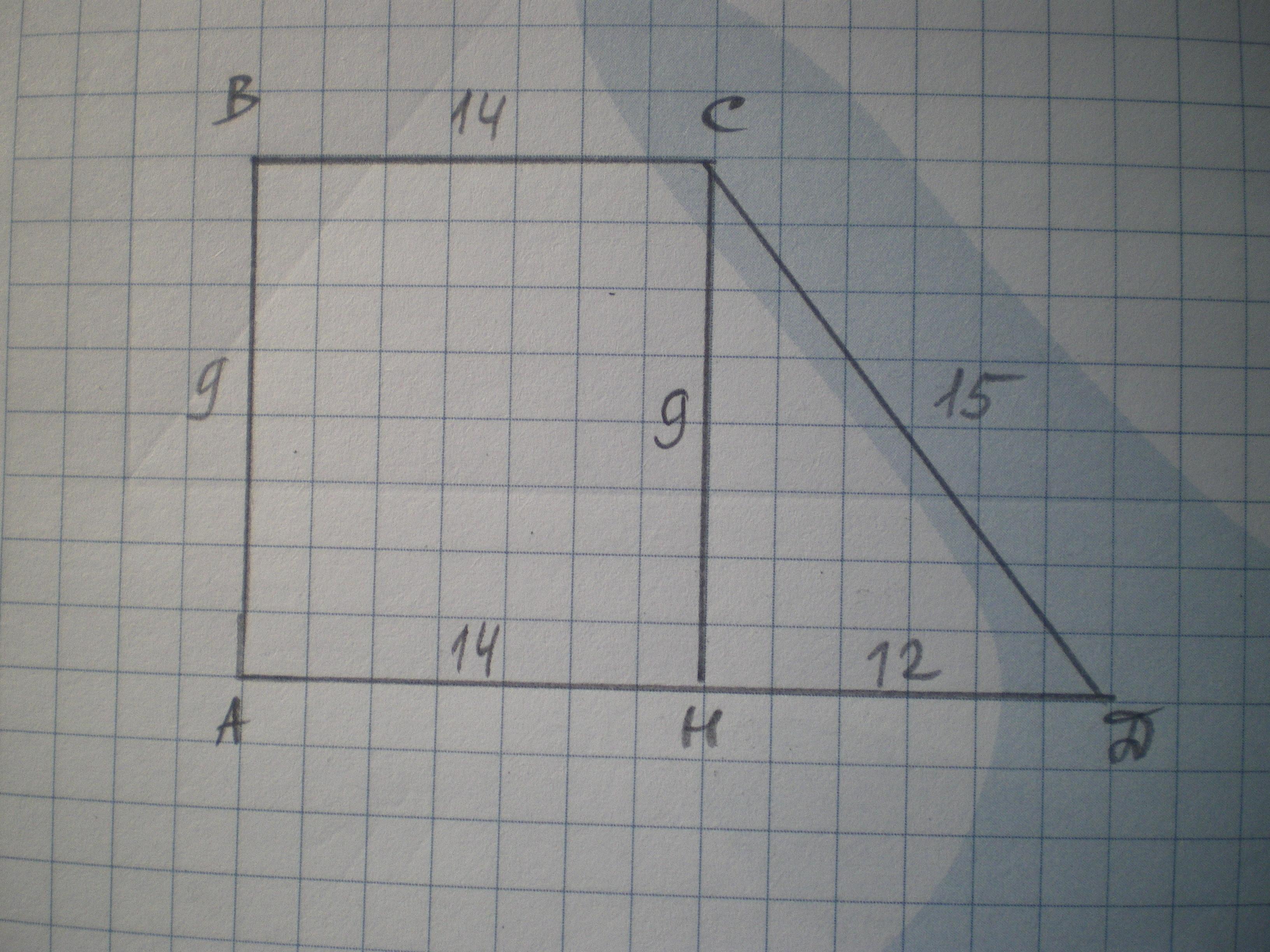
В прямоугольной трапеции боковые стороны равны 9 см и 15 см, а меньшее основание –
14 см. Найдите большее основание трапеции.
1 ответ:
0
0
Дано: АВСД — трапеция, ∠А=∠В=90°, ВС=14 см, СД=15 см. Найти АД.
Проведем высоту СН=АВ=9 см. Найдем ДН по теореме Пифагора из ΔСДН
ДН=√(СД²-СН²)=√(225-81)=√144=12 см.
АД=АН+ДН=14+12=26 см.
Ответ: 26 см.
Читайте также
Если 2 стороны треугольника пересечены прямой параллельной третьей стороне, то треугольник образованный при пересечении подобен начальному, по 3 углам. Так как АБ = 20, ОБ = 4, значит коэффицент подобия 5. ОК : АЦ = 1 : 5. ОК = 2 АЦ = 10
Sinx=a/c Sin45=a/4 a=2корень из2 a=h=d
S=2Sосн +sбок пов S=3ПR^2 + 2ПRh
S=4П +8П= 12П=12*3,14=37,68
на фото……………….
Так как NK медиана, то MK=KP (медиана делит сторону на два равных отрезка)
Так как угол KNP = 32 градуса и NK=KP, то угол NPM=32 градуса
Так как углы NPM и угол PNK в сумме образуют 64 градуса, то угол NKP=180-64=116 градусов
Углы NKP и NKM — смежные, следовательно, угол NKM=180-116=64
Так как NK (медиана)=KP, то NK=MK
MN=MN следовательно треугольник NKM равнобедренный и углы при основании равны. Угол NMP=(180-64)/2
Угол NMP равен 58 градусов
Ответ: угол NPM=32 градуса, угол NMP=58 градусов
<u><em>Треугольник с двумя равными сторонами — равнобедренный</em></u>
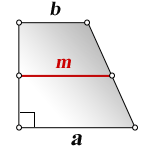
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
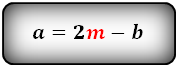
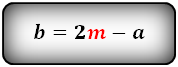
Формулы длины оснований :
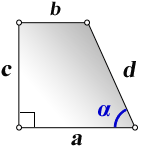
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
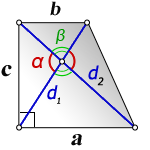
3. Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
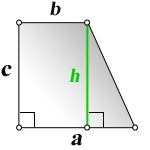
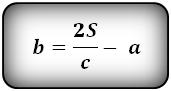
4. Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 15 октября 2013
-
Обновлено: 13 августа 2021