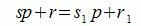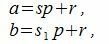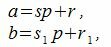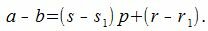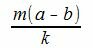Как найти больший модуль числа

Войти

Задать вопрос

Математика

Иля

27 декабря, 18:04

Как узнать какой модуль больше?

+3

Ответы (2)

1. 

   Феодула
   
   27 декабря, 18:40

   
   -1
   

   Чем больше число в модуле, тем больше и сам модуль

   • Комментировать
   • Жалоба
   • Ссылка

2. 

   Эмилия
   
   27 декабря, 20:04

   
   0
   

   Пример

   Есть у нас |-5| И |3|

   Раскрываем модуль

   Получается 5 и 3

   5>3

   • Комментировать
   • Жалоба
   • Ссылка

Знаешь ответ?

Не уверен в ответе?

Найди верный ответ на вопрос ✅ «Как узнать какой модуль больше? …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по математике

2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч

Ответы (3)

В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла

Ответы (1)

Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?

Ответы (2)

Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. Найти периметр.

Ответы (2)

Всем привет. В магазине в 1 день продали 35%, во 2 — 28%всеховощей, А в 3 — оставшиеся 333 кг. Сколько кг овощейбыло в магазине первоначально?

Ответы (3)

Главная » Математика » Как узнать какой модуль больше?

Как взять число по модулю

Программно реализовать вычисление модуля можно с использованием условного оператора ветвления if/then — эта конструкция существует практически в любом языке программирования. Например, чтобы значение, содержащееся в переменной с названием $someNum, заменить его модулем на языке php код строки должен выглядеть так:

if($someNum Pascal эту же операцию можно записать так:

Это очень простая и часто используемая математическая операция, поэтому во всех языках программирования есть встроенная функция, которая позволяет обойтись без условного оператора. Как и в Excel, в большинстве программных языков этой функции присвоено название abs, но есть и исключения — в Си она названа fabs. Синтаксис имеет больше различий и подчиняется правилам конкретного языка. Например, описанный выше пример на языке php можно заменить таким применением функции:

Это очень простая и часто используемая математическая операция, поэтому во всех языках программирования есть встроенная функция, которая позволяет обойтись без условного оператора. Как и в Excel, в большинстве программных языков этой функции присвоено название abs, но есть и исключения — в Си она названа fabs. Синтаксис имеет больше различий и подчиняется правилам конкретного языка. Например, описанный выше пример на языке php можно заменить таким применением функции:

Источник

Решение сравнений по модулю

Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m

Решение сравнений по модулю

Решений нет

Сравнение по модулю

Сравнение двух целых чисел по модулю натурального числа m — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на m один и тот же остаток. Арифметические операции с остатками чисел по одному и тому же модулю образуют модулярную арифметику.

Сравнимость чисел a и b по модулю сравнения m записывается как

называется сравнением первой степени или линейным сравнением по модулю m.

Для проверки существования решений сравнения сначала вычисляется НОД(a, m). Если b не кратно полученному НОД, то у сравнения нет решений.
Если кратно, то количество решений по модулю m равно полученному НОД.

Существует несколько алгоритмов нахождения всех решений сравнения, но в данном калькуляторе применяется алгоритм решения линейных диофантовых уравнений с двумя переменными. В самом деле, сравнение эквивалентно следующему линейному диофантовому уравнению:

поэтому я использовал уже реализованный калькулятор решения линейных диофантовых уравнений для получения общей формулы решения, после чего выбрал все частные решения в диапазоне от 0 до m.

Источник

Модуль числа

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

−(a · b), когда a · b

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.

Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.

Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.

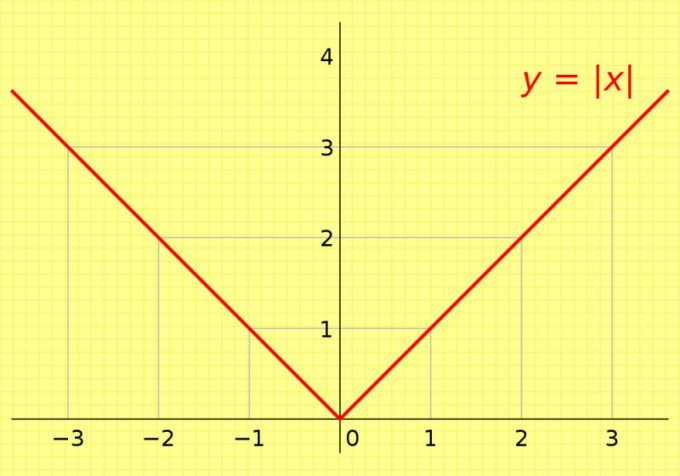
График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √ a 2 , где a – некоторое число или выражение.

При этом, √ a 2 = |a|.

По определению арифметического квадратного корня √ a 2 — это такое неотрицательное число, квадрат которого равен a 2 .

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

У нас есть комплексное число, которое выглядит следующим образом: z = x + i · y, где x представляет собой действительную, а i · y — мнимую части комплексного числа z (и оба являются действительными числами), а i — мнимая единица и равна √ -1

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

• Область определения: вся комплексная плоскость.
• Область значений: [0;+∞).

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

• Область определения: (−∞;+∞).
• Область значений: [0;+∞).
• Функция чётная.
• Функция дифференцируется везде, кроме нуля. В точке x=0 функция претерпевает излом.

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

• Противоположные числа имеют равные модули, то есть |- а| = |а| = a.
  Если посмотреть это относительно координатной прямой, то две точки, у которых координаты — это противоположные числа, располагаются на одном расстоянии от начала отсчета. То есть модули противоположных чисел одинаковы.
• Модуль нуля равен нулю.
  |0| = 0, если a = 0
• Для положительного числа модуль равен самомý числу, а для отрицательного – противоположному числу.
  |а| = а
  |−a| = a

Источник

Сравнение чисел по модулю

Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.

Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде

где s — число, и r одно из чисел 0,1, . p−1.

1 ) В данной статье под словом число будем понимать целое число.

Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа

Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.

Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s₁p+r₁. Тогда

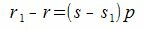(2)

Так как r₁ принимает один из чисел 0,1, . p−1, то абсолютное значение r₁−r меньше p. Но из (2) следует, что r₁−r кратно p. Следовательно r₁=r и s₁=s.

Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).

Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.

Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда

где s и s₁ некоторые целые числа.

Разность этих чисел

(3)

делится на p, т.к. правая часть уравнения (3) делится на p.

Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.

Доказательство. Обозначим через r и r₁ остатки от деления a и b на p. Тогда

По утверждению a−b делится на p. Следовательно r−r₁ тоже делится на p. Но т.к. r и r₁ числа 0,1. p−1, то абсолютное значение |r−r₁| Свойство 1. Для любого a и p всегда

Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если

a≡b mod (p), b≡c mod (p).

Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.

a≡b mod (p) и m≡n mod (p),

a+m≡b+n mod (p) и a−m≡b−n mod (p).

Действительно. Так как a−b и m−n делятся на p, то

(a−b)+ (m−n)=(a+m)−(b+n) ,

также делятся на p.

Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.

a≡b mod (p) и m≡n mod (p),

Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно

Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит

Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).

где k некоторое неотрицательное целое число.

Действительно. Имеем a≡b mod (p). Из свойства 4 следует

Все свойства 1-5 представить в следующем утверждении:

Утверждение 4. Пусть f(x₁, x₂, x₃, . ) целая рациональная функция с целыми коэффициентами и пусть

a₁≡b₁, a₂≡b₂, a₃≡b₃, . mod (p).

f(a₁, a₂, a₃, . )≡f(b₁, b₂, b₃, . ) mod (p).

При делении все обстоит иначе. Из сравнения

не всегда следует сравнение

Утверждение 5. Пусть

Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда

Так как m(a−b) делится на k, то

имеет нулевой остаток. Тогда

имеет нулевой остаток, т.е. m₁(a−b) делится на k₁. Но числа m₁ и k₁ числа взаимно простые. Следовательно a−b делится на k₁=k/λ и, тогда, a≡b mod (p/λ).

Утверждение 6. Если

и m является один из делителей числа p, то

Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.

Утверждение 7. Если

a≡b mod (p), a≡b mod (q), a≡b mod (s)

где h наименьшее общее кратное чисел p,q,s.

Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.

В частном случае, если модули p,q,s взаимно простые числа, то

Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.

Источник

Okay, so you want to calculate a^b mod m. First we’ll take a naive approach and then see how we can refine it.

First, reduce a mod m. That means, find a number a1 so that 0 <= a1 < m and a = a1 mod m. Then repeatedly in a loop multiply by a1 and reduce again mod m. Thus, in pseudocode:

a1 = a reduced mod m
p = 1
for(int i = 1; i <= b; i++) {
    p *= a1
    p = p reduced mod m
}

By doing this, we avoid numbers larger than m^2. This is the key. The reason we avoid numbers larger than m^2 is because at every step 0 <= p < m and 0 <= a1 < m.

As an example, let’s compute 5^55 mod 221. First, 5 is already reduced mod 221.

1. 1 * 5 = 5 mod 221
2. 5 * 5 = 25 mod 221
3. 25 * 5 = 125 mod 221
4. 125 * 5 = 183 mod 221
5. 183 * 5 = 31 mod 221
6. 31 * 5 = 155 mod 221
7. 155 * 5 = 112 mod 221
8. 112 * 5 = 118 mod 221
9. 118 * 5 = 148 mod 221
10. 148 * 5 = 77 mod 221
11. 77 * 5 = 164 mod 221
12. 164 * 5 = 157 mod 221
13. 157 * 5 = 122 mod 221
14. 122 * 5 = 168 mod 221
15. 168 * 5 = 177 mod 221
16. 177 * 5 = 1 mod 221
17. 1 * 5 = 5 mod 221
18. 5 * 5 = 25 mod 221
19. 25 * 5 = 125 mod 221
20. 125 * 5 = 183 mod 221
21. 183 * 5 = 31 mod 221
22. 31 * 5 = 155 mod 221
23. 155 * 5 = 112 mod 221
24. 112 * 5 = 118 mod 221
25. 118 * 5 = 148 mod 221
26. 148 * 5 = 77 mod 221
27. 77 * 5 = 164 mod 221
28. 164 * 5 = 157 mod 221
29. 157 * 5 = 122 mod 221
30. 122 * 5 = 168 mod 221
31. 168 * 5 = 177 mod 221
32. 177 * 5 = 1 mod 221
33. 1 * 5 = 5 mod 221
34. 5 * 5 = 25 mod 221
35. 25 * 5 = 125 mod 221
36. 125 * 5 = 183 mod 221
37. 183 * 5 = 31 mod 221
38. 31 * 5 = 155 mod 221
39. 155 * 5 = 112 mod 221
40. 112 * 5 = 118 mod 221
41. 118 * 5 = 148 mod 221
42. 148 * 5 = 77 mod 221
43. 77 * 5 = 164 mod 221
44. 164 * 5 = 157 mod 221
45. 157 * 5 = 122 mod 221
46. 122 * 5 = 168 mod 221
47. 168 * 5 = 177 mod 221
48. 177 * 5 = 1 mod 221
49. 1 * 5 = 5 mod 221
50. 5 * 5 = 25 mod 221
51. 25 * 5 = 125 mod 221
52. 125 * 5 = 183 mod 221
53. 183 * 5 = 31 mod 221
54. 31 * 5 = 155 mod 221
55. 155 * 5 = 112 mod 221

Therefore, 5^55 = 112 mod 221.

Now, we can improve this by using exponentiation by squaring; this is the famous trick wherein we reduce exponentiation to requiring only log b multiplications instead of b. Note that with the algorithm that I described above, the exponentiation by squaring improvement, you end up with the right-to-left binary method.

a1 = a reduced mod m
p = 1
while (b > 0) {
     if (b is odd) {
         p *= a1
         p = p reduced mod m
     }
     b /= 2
     a1 = (a1 * a1) reduced mod m
}

Thus, since 55 = 110111 in binary

1. 1 * (5^1 mod 221) = 5 mod 221
2. 5 * (5^2 mod 221) = 125 mod 221
3. 125 * (5^4 mod 221) = 112 mod 221
4. 112 * (5^16 mod 221) = 112 mod 221
5. 112 * (5^32 mod 221) = 112 mod 221

Therefore the answer is 5^55 = 112 mod 221. The reason this works is because

55 = 1 + 2 + 4 + 16 + 32

so that

5^55 = 5^(1 + 2 + 4 + 16 + 32) mod 221
     = 5^1 * 5^2 * 5^4 * 5^16 * 5^32 mod 221
     = 5 * 25 * 183 * 1 * 1 mod 221
     = 22875 mod 221
     = 112 mod 221

In the step where we calculate 5^1 mod 221, 5^2 mod 221, etc. we note that 5^(2^k) = 5^(2^(k-1)) * 5^(2^(k-1)) because 2^k = 2^(k-1) + 2^(k-1) so that we can first compute 5^1 and reduce mod 221, then square this and reduce mod 221 to obtain 5^2 mod 221, etc.

The above algorithm formalizes this idea.

Ниже представлены правила сравнения модулей положительных и отрицательных чисел. Также приведены примеры для лучшего понимания теоретического материала.

• Правила сравнения модулей
  • Положительные числа

  • Отрицательные числа

Правила сравнения модулей

Положительные числа

Модули положительных чисел сравниваются таким же образом, что и действительные числа.

Примеры:

• |6| > |4|
• |15,7| < |9|
• |20| = |20|

Отрицательные числа

1. Если модуль одного из отрицательных чисел меньше другого, что это число является бОльшим.
2. Если модуль одного из отрицательных чисел больше другого, что это число является меньшим.
3. Если модули отрицательных числе равны, то равны и эти числа.

Примеры:

• |-7| < |-3|
• |-5| > |-14,6|
• |-17| = |-17|

Примечание:

На координатной оси бОльшее отрицательное число находится правее меньшего.