Как найти большую часть ромба - Исправление недочетов и поиск решений вместе с Examum.ru

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Ромб и его свойства

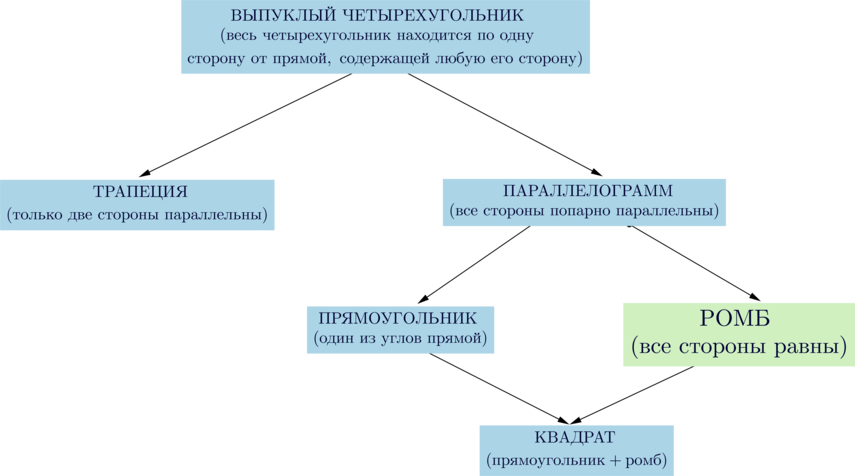
Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства ромба:

(blacktriangleright) Те же, что и у параллелограмма:

(sim) Противоположные стороны попарно равны;

(sim) Диагонали точкой пересечения делятся пополам;

(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);

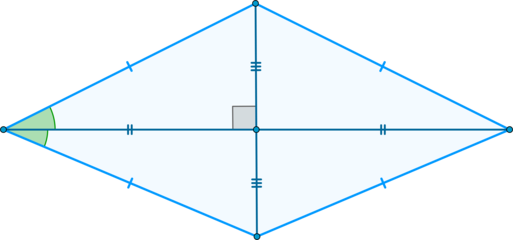
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.

Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:

(blacktriangleright) все стороны равны;

(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;

(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.

Площадь ромба

1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1

#2716

Уровень задания: Легче ЕГЭ

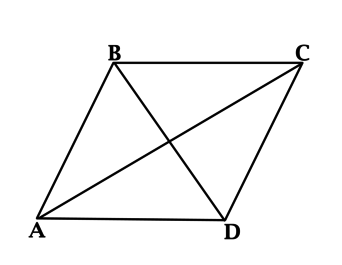
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.

В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).

(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).

Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).

Ответ: 64

Задание
2

#2717

Уровень задания: Равен ЕГЭ

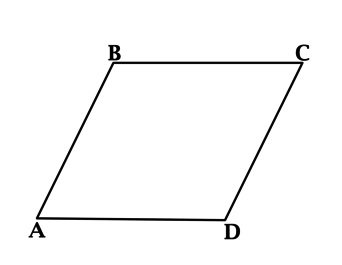
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).

Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).

Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).

Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).

Ответ: 6

Задание
3

#2715

Уровень задания: Равен ЕГЭ

Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.

Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).

Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.

Ответ: 10

Задание
4

#1794

Уровень задания: Равен ЕГЭ

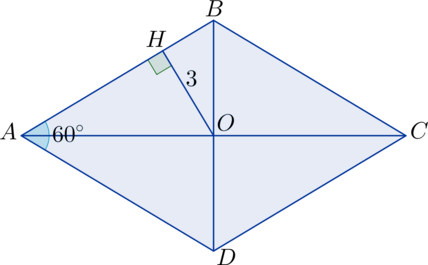
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.

Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).

Ответ: 12

Задание
5

#1757

Уровень задания: Равен ЕГЭ

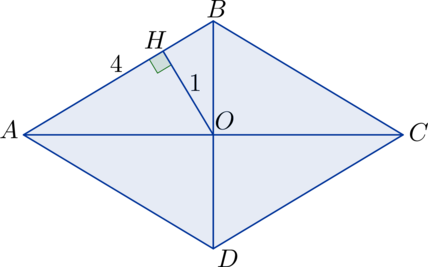
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.

Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = .

Ответ: 8

Задание
6

#2718

Уровень задания: Равен ЕГЭ

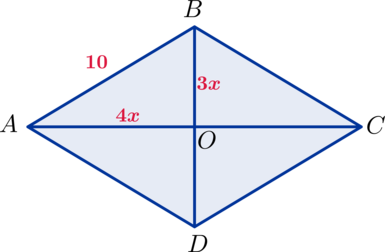
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.

Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).

Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).

Ответ: 96

Задание
7

#2719

Уровень задания: Равен ЕГЭ

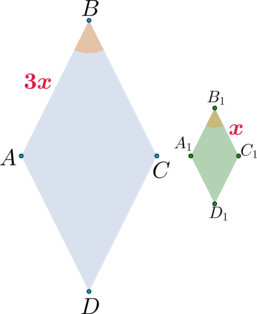
Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?

Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.

Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).

Ответ: 9

Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.

Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.

Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.

Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.

Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Ромб. Формулы, признаки и свойства ромба

Определение.

Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.

Ромбы отличаются между собой размером стороны и размером углов.

Признаки ромба

Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:

1. Две его смежные стороны равны (отсюда следует, что все стороны равны):

АВ = ВС = СD = AD

2. Его диагонали пересекаются под прямым углом:

AC┴BD

3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:

∠BAC = ∠CAD или ∠BDA = ∠BDC

4. Если все высоты равны:

BN = DL = BM = DK

5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Если в параллелограмм можно вписать круг.

Основные свойства ромба

2. Диагонали перпендикулярны:

AC┴BD

3. Диагонали являются биссектрисами его углов:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:

AC² + BD² = 4AB²

5. Точка пересечения диагоналей называется центром симметрии ромба.

6. В любой ромб можно вписать окружность.

7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Определение.

Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.

Ромб имеет две диагонали — длинную d₁, и короткую — d₂

Формулы определения длины диагонали ромба:

1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 — 2 · cosβ

2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)

d₂ = a√2 + 2 · cosβ

d₂ = a√2 — 2 · cosα

3. Формулы большой диагонали ромба через сторону и половинный угол:

d₁ = 2a · cos(α/2)

d₁ = 2a · sin(β/2)

4. Формулы малой диагонали ромба через сторону и половинный угол:

d₂ = 2a · sin(α/2)

d₂ = 2a · cos(β/2)

5. Формулы диагоналей ромба через сторону и другую диагональ:

d₁ = √4a² — d₂²

d₂ = √4a² — d₁²

6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:

d₁ = d₂ · tg(β/2)

d₂ = d₁ · tg(α/2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Определение.

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Формула периметра ромба через сторону ромба:

P = 4a

Площадь ромба

Определение.

Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.

Формулы определения площади ромба:

1. Формула площади ромба через сторону и высоту:

S = a · h_a

2. Формула площади ромба через сторону и синус любого угла:

S = a² · sinα

3. Формула площади ромба через сторону и радиус:

S = 2a · r

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):

Окружность вписанная в ромб

Определение.

Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Источник

Начнем с того что у ромба две диагонали.

Одна большая D, а другая маленькая d.

Рассмотрим способы нахождения большой диагонали D.

D=a*sqrt(2-2*cos(?)=a*sqrt(2+2*cos(?);
D=sqrt(4*sqr(a)-sqr(d));

Также D находится по площади ромба и малой диагонали:

D=(2*S)/d;

Рассмотрим способы нахождения меньшей диагонали d.

d=a*sqrt(2-2*cos(?))=a*sqrt(2+2*cos(?);
D=sqrt(4*sqr(a)-sqr(D));

Малую диагональ d тоже можно найти через площадь ромба и большую диагональ:

d=(2*S)/D;

автор вопроса выбрал этот ответ лучшим

Alexsandr82
[21.4K]

6 лет назад

У ромба есть две диаганали: большая (d1) и малая (d2), а также углы а — острый угол ромба (в ромбе два острых угла и оба равны между собой), и b — тупой угол (их тоже два и они тоже равны). Если нам известна сторона ромба (x) и один из углов то мы можем найти любую диагональ по формулам:

d1 = 2x*cos(a/2)

d2 = 2x*sin(a/2)

Или

d1 = 2x*sin(b/2)

d2 = 2x*cos(b/2)

Кроме этого если нам извесна площадь ромба и одна из диагоналей мы можем найти вторую диагональ по формулам:

d1 = 2S/d2

d2 = 2S/d1

Если нам дан радус вписанной в ромб окружности и любой из углов мы также можем рассчитать диагональ ромба:

d1 = 2r/sin(a/2)

d2 = 2r/sin(b/2)

Где r — радиус вписанной окружности.

Знаете ответ?

Источник

Как найти больший угол ромба

Ромбом называют четырехугольник, у которого все стороны одинаковы, а углы не равны. Эта геометрическая фигура обладает уникальными свойствами, которые значительно облегчают расчеты. Чтобы найти ее больший угол, нужно знать еще несколько параметров.

Вам понадобится

— таблица синусов;
— таблица косинусов;
— таблица тангенсов.

Инструкция

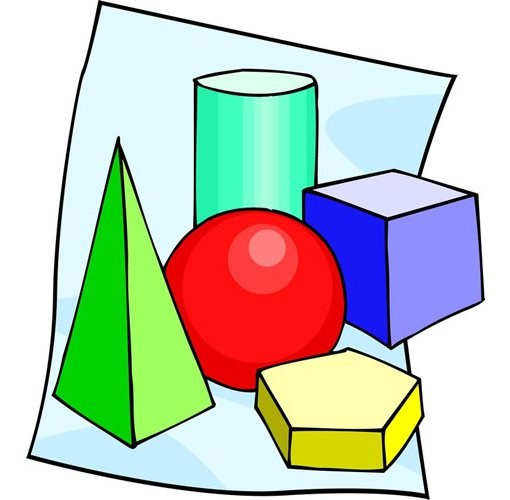
В условиях задачи может быть указан меньший угол. Вспомните, чему равна сумма углов, прилежащих к одной стороне. Она у любого ромба составляет 180°. То есть вам достаточно из 180° вычесть размер известного угла. Начертите ромб. Обозначьте больший угол как α, а меньший – как β. Формула в этом случае будет выглядеть как α=180°-β.

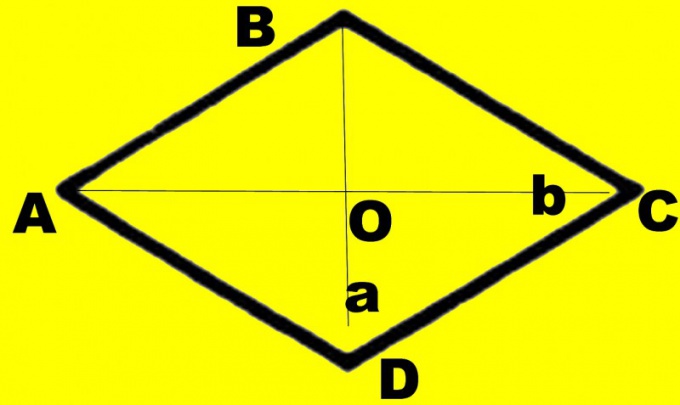
В задаче могут быть указаны также размер стороны и длина одной из диагоналей. В этом случае нужно вспомнить свойства диагоналей ромба. В точке пересечения они делятся пополам. Диагонали перпендикулярны друг другу, то есть при решении задачи можно будет использовать свойства прямоугольных треугольников. Еще одна важная деталь каждая из диагоналей одновременно является и биссектрисой угла.

Для наглядности сделайте чертеж. Начертите ромб ABCD. Проведите в нем диагонали d1 и d2. Допустим, известная вам диагональ d1 соединяет меньшие углы. Обозначьте точку их пересечения как О, большие углы ABC и CDA– как α, а меньшие – как β. Каждый из углов делится диагональю пополам. Рассмотрите прямоугольный треугольник АОВ. Вам известны стороны АВ и ОА, равная половине диагонали d1. Они представляют собой гипотенузу и катет противолежащего угла.

Вычислите синус угла АВО. Он равен отношению катета ОА к гипотенузе АВ, то есть sinАВО= ОА/АВ. По таблице синусов найдите размер угла. Вспомните, что он равен половине большего угла ромба. Соответственно, для определения искомого полученный размер умножьте на 2.

Если в условиях дан размер диагонали d2, соединяющей большие углы, способ решения будет аналогичен предыдущему, только вместо синуса используется косинус – отношение прилежащего катета к гипотенузе.

В условиях могут быть заданы только размеры диагоналей. В этом случае тоже понадобится чертеж, но, в отличие от предыдущих задач, он может быть точным. Проведите диагональ d1. Разделите ее пополам. К точке пересечения проведите диагональ d2 так, чтобы она тоже делилась на две равные части. Концы отрезков соедините по периметру. Обозначьте ромб как ABCD, точку пересечения диагоналей – как О.

Сторону ромба в данном случае вам вычислять не нужно. У вас образовался прямоугольный треугольник АОВ, у которого вам известны два катета. Отношение противолежащего катета к прилежащему называется тангенсом. Чтобы найти tgАВО, разделите ОА на ОВ. Найдите в таблице тангенсов нужное значение угла, а затем умножьте его на два.

Некоторые компьютерные программы позволяют не только вычислить больший угол ромба по заданным параметрам, но и сразу же начертить эту геометрическую фигуру. Это можно сделать, например, в программе AutoCAD. В этом случае таблицы синусов и тангенсов, конечно же, не нужны.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Содержание:

Формулы площади ромба:
Формула периметра ромба:

Ромб — это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.

Формулы площади ромба:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.

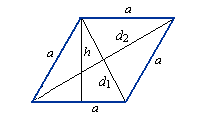
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

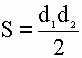
S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d₁ — длина 1-ой диагонали

d₂ — длина 2-ой диагонали

См. также: Программа для расчета площади ромба.

Формула периметра ромба:

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.

1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).

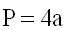
P — периметр ромба

a — длина стороны ромба

Остались вопросы?

Здесь вы найдете ответы.

Что понимается под высотой ромба?

Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.

Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?

Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.

Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:

BAH=180-30-90=60 градусов.

Так, угол АВС равен:

ABC=180-60=120 градусов.

Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?

Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:

S = a*h.

Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:

h = S/a.

Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?

Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:

SΔ = 4*3/2 = 6 см.кв.

Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:

S = 5*x = 6 см.кв.

Отсюда можно найти значение х:

х = 6/5 = 1,2 см.

Ответ: высота ромба составляет 1,2 см.

Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?

Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:

с = √(9+16) = √25 = 5 см.

Следовательно, сторона ромба также равна 5 см.

Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:

S = d1*d2/2 = 6*8/2 = 24 см. кв.

Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):

S = a*h

Из данной формулы выражаем высоту:

h = S/a = 24/5 = 4,8 см.

Ответ: Высота ромба составляет 4,8 см.

Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?

Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:

h = (d1 * d2)/a

Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?

Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:

Р = а+а+а+а

В данном случае периметр ромба равен 48 см., это значит, что:

а+а+а+а = 48 см.

Находим значение а:

а = 48/4 = 12 см.

Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:

S = а*h

В задании сказано, что площадь ромба – 60 см.кв. Значит:

а*h=60

Находим неизвестную высоту:

h=60/а=60/12=5 см.

Ответ: Высота ромба – 5 см.

Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?

Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:

а = Р/4 = 32/4 = 8 см.

Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:

S = а* h

В конкретном случае:

48 = 8* h

Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:

H = 48/8 = 6 см.

Ответ: Высота ромба составляет 6 см.

Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?

Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:

Р = 4*а

По условию задачи:

52 = 4*а

Следовательно:

а = 52/13 = 13 см.

Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:

10х:24х=10:24

Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.

Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:

с2 = а2 + b2

Для данной задачи это равенство записывается так:

(5х)²+(12х)²=13²

Отсюда видно, что:

169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.

Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).

Площадь (S) ромба рассчитывается как:

S = d₁*d₂/2 или a·h

Из этого можно составить следующее уравнение:

d₁*d₂=2a*h

Выражаем h и получаем:

h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.

Какая формула используется с целью вычисления высоты ромба?

Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.

Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.

Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.

В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:

h = a*a*sin A /a = a*sin A.

Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.

В каком виде записываются формулы, используемые для определения площади
ромба?

Площадь ромба можно рассчитать одним из трех способов:

1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.

2. S = ah, или Длина стороны ромба, умноженная на его высоту.

3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.

На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?

Зная, чему равен периметр ромба, можно вычислить длину его стороны:

Р/4 = 8 см.

Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:

h = 8-1,7 = 6,3 см.

Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:

8 * 6,3 = 50,4 см².кв.

Ответ: S = 50,4 см. кв.

Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?

Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:

(4d)²+(3d)²=10² = 16d²+9d² = 100

Отсюда:

25d²=100

d =2,

Значит:

d¹/2 = 4d = 8 см.

d²/2 = 3d = 6 см.

Теперь можно найти площадь:

S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.

Ответ: S ромба = 96 см.кв.

Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?

Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:

S = ½ d1*d2.

Как записать формулу вычисления площади ромба через диагонали?

Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.

Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:

S = ½ d1*d2.

Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:

S=1/2*5*4=10 см. кв.

Как выглядит формула для определения площади ромба?

S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:

S=a*h.

См. также: Программа для расчета периметра ромба.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник