Как найти большую полуось орбиты спутника

Сегодня речь пойдет о конфигурации планет.

Конфигурация — характерное взаимное положение Солнца, планет, других небесных тел Солнечной системы на небесной сфере.

Будем называть планеты нижними, если они расположены ближе к Солнцу, чем Земля. Остальные планеты будут верхними – они расположены дальше нашей планеты от Солнца.

Планета может расположиться так, что Земля, Солнце и указанная планета находятся на одной линии. При этом может оказаться, что Солнце расположилось между Землей и рассматриваемой планетой. Такое расположение будем называть верхним соединением. Если же планета оказалась между Землей и Солнцем – то это уже нижнее соединение. Также может быть, что Земля находится между верхней планетой и Солнцем – тогда речь пойдет о противостоянии, или оппозиции.

Элонгация — одна из конфигураций планет, такое положение планеты, при котором её угловое расстояние от Солнца максимально для земного наблюдателя. Различают восточную и западную элонгацию (планета находится, соответственно, к востоку и к западу от Солнца). Об элонгации имеет смысл говорить только для Венеры и Меркурия; наилучшие условия для наблюдения этих планет наступают именно вблизи элонгаций. Из-за того, что орбиты планет не вполне круговые, угловое расстояние от Солнца в момент элонгации может быть разным, для Меркурия — от до , для Венеры — около .

Квадратура — в астрономии такая конфигурация Луны или верхней планеты (то есть планеты, более удалённой от Солнца, чем Земля) относительно Земли и Солнца, когда угол планета-Земля-Солнце равен . Если светило при этом находится к востоку от Солнца, конфигурация называется восточной квадратурой, к западу — западной квадратурой.

Сидерический период — это время совершения полного оборота какого-либо тела (планеты, кометы, астероида или искусственного спутника) вокруг главного тела (Солнца или др. планеты для спутника планеты) относительно неподвижных звёзд. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п.

Синодический же период — это время наблюдения с Земли совершения полного оборота планеты вокруг Солнца или Луны (искусственного спутника) вокруг Земли относительно Солнца ; промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.

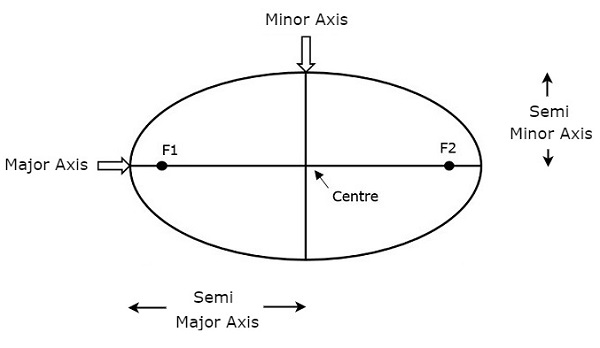
Будем помнить также и о том, что орбиты планет не круговые. Это эллипсы, причем Солнце находится в одном из главных фокусов орбиты планеты.

Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.

Антонимом перигелия является афелий (апогелий) — наиболее удалённая от Солнца точка орбиты. Воображаемую линию между афелием и перигелием называют линией апсид.

Названия апоцентров меняются: эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:

Задача 9.

Центральное тело	Греческое название	Наименование перицентра	Наименование апоцентра
Солнце	Гелиос	перигелий	афелий
Земля	Гея	перигей	апогей
Венера	Геспер	перигесперий	апогесперий
Марс	Арес	периарий	апоарий
Сатурн	Кронос	перикроний	апокроний
Луна	Селена	периселений	апоселений

Теперь обратимся к математике и разберемся, что же такое эксцентрисистет. Будем говорить об эксцентриситете эллипса, поскольку нас пока больше интересуют орбиты планет.

Эксцентриситетом эллипса называется отношение рас­стояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой  , получаем:

Так как , то , т. е. эксцентриситет каждого эллипса меньше единицы. Заметим, что , поэтому

Или

И

Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, опреде­ляется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение  ; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности  и  .

Радиус перигелия рассчитывается по формуле:

где:

 — большая полуось;

 — эксцентриситет орбиты.

Скорость в перигелии рассчитывается по формуле:

где:

 — гравитационная постоянная;

 — масса Солнца;

 — большая полуось;

 — эксцентриситет орбиты.

Афелийное расстояние рассчитывается по формуле

Следовательно, большая полуось орбиты планеты является средним  ее расстоянием от Солнца

Cидерические периоды обращения и двух планет связаны с их средними расстояниями и от Солнца третьим законом Кеплера

Если  дается в годах   и   — в   астрономических единицах, то, принимая для Земли год и а. е., получим для любой планеты

Средняя орбитальная, или круговая, скорость планеты

всегда выражается в км/с. Так как обычно задается в астрономических единицах (1 а. е.= км) и T— в годах (1 год= с), то

Подставляя , получим:

Где скорость планеты теперь выражена в км/с.

Средняя продолжительность синодического периода обращения планеты связана с сидерическим периодом уравнением синодического движения:  для  верхних планет

для нижних планет

где — сидерический период обращения Земли, равный 1 звездному году.

Задача 1.

Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144.

Перигельное расстояние, а.е.

афелийное расстояние, а.е.

Сидерический период обращения

а так как а. е., то планета верхняя и поэтому ее синодический период обращения вычисляется по формуле

при году:

Круговая скорость, км/с:

Задача 2.

Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е., а эксцентриситеты орбит— 0,054 и 0,008.

Перигельное расстояние Сатурна, а.е.

афелийное расстояние Сатурна, а.е.

Перигельное расстояние Нептуна, а.е.

афелийное расстояние Нептуна, а.е.

Ответ: а.е., а.е., а.е., а.е.

Задача 3.

Какая из двух планет — Нептун (а = 30,07 а.е., ) или Плутон (а = 39,52 а. е., )    —     подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты  планеты.

Нужно сравнить перигельные расстояния, причем для Нептуна мы его уже вычислили: а.е. Вычислим для Плутона:

Таким образом, Плутон ближе подходит к Солнцу.

Задача 4.

Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу.

Опять определим перигельные расстояния. Наибольшие расстояния от Солнца нам известны – афелийные. Тогда для Марса

Следовательно, перигельное расстояние Марса равно

Для Адониса

Следовательно, перигельное расстояние Адониса равно

Таким образом, Адонис подходит ближе к Солнцу.

Ответ: , а.е. , , а.е.

Задача 5.

На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно?

Так как афелийное расстояние у Симеизы больше, то радиус-вектор ее длиннее (абсолютно). Но, так как , то относительно радиус-вектор Икара больше изменяется.

Задача 6.

Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е.

Сидерический период Венеры равен:

Или 224,5 суток.

Сидерический период астероида Европы равен:

Ответ: сидерический период Венеры равен 0,615 года или 224,5 суток, а у Европы 5,458 года.

Задача 7.

Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно.

Определим большие полуоси орбит Аполлона и кометы Икейи:

Тогда сидерический период Аполлона

Тогда сидерический период Икейи

Ответ: года, лет.

Задача 8.

Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км?

Для спутников справедлив закон Кеплера. Применим его для Европы:

Период 42ч28м= ч.

А теперь то же самое для Ганимеда:

Ответ: Период Европы 85,23 ч, или 3^д 55, период Ганимеда 171,59 ч, или 7^д 15

Задача 9.

Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4^д,518. Самый крупный спутник планеты — Титан, обращается за 15^д,945 по орбите с большой полуосью в 1221 тыс. км.

Переведем периоды в часы: период Мимаса 22,62 ч, период Реи 108,43 ч, период Титана 382, 68 ч.

Применяем закон Кеплера для Титана и Мимаса:

То же для Реи:

Ответ: большая полуось Мимаса 185,27 тыс. км, Реи 526,7 тыс. км.

1. Элементы орбиты и законы Кеплера. Основные формулы невозмущённого движения.

От постоянных интегрирования
обычно переходят к другим параметрам,
по которым можно вычислять координаты
и скорости спутника на любой момент
времени в инерциальной системе отсчёта.
Их называют элементами орбиты. По своему
назначению элементы орбиты делятся на
три группы. К первой группе относят
элементы, характеризующие размеры и
форму орбиты. Это большая полуосьи эксцентриситет обиты е:

К этой же группе элементов относятся:
фокальный параметр
,
малая полуось,
радиусы орбиты в перигееи
апогее:

а так же период обращения и среднее
движение:

Периодом обращения спутника
вокруг центрального тела называется
промежуток времени между моментами
двух последовательных прохождений
через произвольную точку орбиты. Среднее
движениеинтерпретируется
как средняя угловая скорость движения
спутника.

Элементы второй группы задают ориентировку
орбиты в пространстве. Они связаны с
векторными интегралами площадей и
Лапласа. К этим элементам относятся:
наклонение
,
долготаи аргумент перигея.

Наклонениемназывают угол между
плоскостью экватора и плоскостью орбиты.
Его можно вычислить по формуле:

Очевидно, что
.
Орбиты с наклонением, равным 0º или 180º
называют экваториальными, а с наклонением
90º– полярными. Орбиты сназывают с прямым движением спутника,
а с– орбиты с обратным движением спутника
( по отношению к направлению вращения
Земли).

Долготой орбитыназывается угол,
отсчитываемый в плоскости экватора от
направления на точку весеннего
равноденствия
(нуль-пункта небесной системы координат)
до направления на восходящий узел орбиты
.
Долготу определяют по формуле:

Аргументом перигеяназывается уголмежду направлениями на восходящий узел
и на перигей, отсчитываемый по направлению
движения спутника:

.

Для долготы и аргумента перигея
справедливо:
,.

Элементы третьей группы задают положение
спутника на орбите. Оно устанавливается
с помощью момента прохождения перигея
или любой из аномалий (обычно истинной
или средней) с указанием эпохи.Истинной аномалиейназывается угол между направлениями
на перигей и на спутник, отсчитываемый
в сторону движения спутника:

Средняя аномалияпредставляет
собой угол от направления на перигей
до направления на некоторое фиктивное
положение спутника, движущегося
равномерно по орбите:

.

Уравнение для средней аномалии иногда
называют динамическим интегралом, в
котором содержится шестая независимая
постоянная интегрирования – момент
проходжения перигея
.

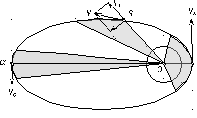
Для связи истинной и средней аномалии
вводится эксцентрическая аномалия.
Чтобы её показать, вокруг орбитального
эллипса описывается окружность с центром
в точке С – геометрическом центре
эллипса, с радиусом, равным его большей
полуоси.
Через положение спутника – точку–
проводится перпендикуляр к большей
полуосидо
пересечения с окружностью в точке.
Соединяются точки С и.
Угол,
отсчитываемый при центре эллипса от
направления на перигей до направления
на точку,
называетсяэксцентрической аномалией.
Истинная и эксцентрическая аномалии
связаны соотношением:

,

а средняя и эксцентрическая аномалии
связаны уравнением Кеплера:

.

Часто используется угол от направления
на восходящий узел до направления на
спутник, называемый аргументом широты:

.

Существует множество других систем
элементов. Приведенные здесь параметры
называют Кеплеровыми элементами орбиты.

Законы движения спутника вокруг
центрального тела были открыты И.Кеплером
в начале XVIIв. Выведенные
вначале для вращающихся вокруг Солнца
планет, они оказались пригодными для
всех других тел, поскольку в их основе
лежит закон всемирного тяготения.

1-й закон Кеплера. Движение спутника
вокруг притягивающего тела всегда
происходит по коническому сечению
(окружности, эллипсу, параболе, гиперболе,
прямой), в одном из фокусов которого
находится притягивающий центр. Закон
выражается с помощью уравнения орбиты,
имеющей вид:

.

В зависимости от величины эксцентриситета
различают отбиты в виде окружности
(е=0), эллипса (0 < е < 1), параболы (е = 1),
гиперболы (е > 1) и прямой (е = ∞). В
дальнейшем мы будем рассматривать
только эллиптические орбиты.

Для описания 2-го закона Кеплера
потребуется ввести понятие секториальной
скорости
.
Это площадь, описываемая радиусом-вектором
спутника за единицу времени. Она связана
со скалярной константой площадей С:

.

Площадь, описываемую радиусом-вектором
спутника за промежуток времени
,
можно получить в виде определённого
интеграла:

,

что является математической записью
2-го закона Кеплера: за равные
промежутки времени радиус-вектор
спутника описывает равные площади.
Вследствии этого, линейная скорость
движения спутника по орбите в перигеебольше,
чем скорость в апогее.

3-й закон Кеплераформулируется
следующим образом: квадраты периодов
обращения спутников пропорциональны
кубам больших полуосей. Математическое
выражение для него получается из формулыЕсли у центрального тела (Земли) имеется
два спутника, соответственно, с периодамиР₁ иР₂и с большими полуосями

и,
то для квадратов их периодов можно
записать:

А отношение этих выражение даёт формулу
3-го закона Кеплера:
.

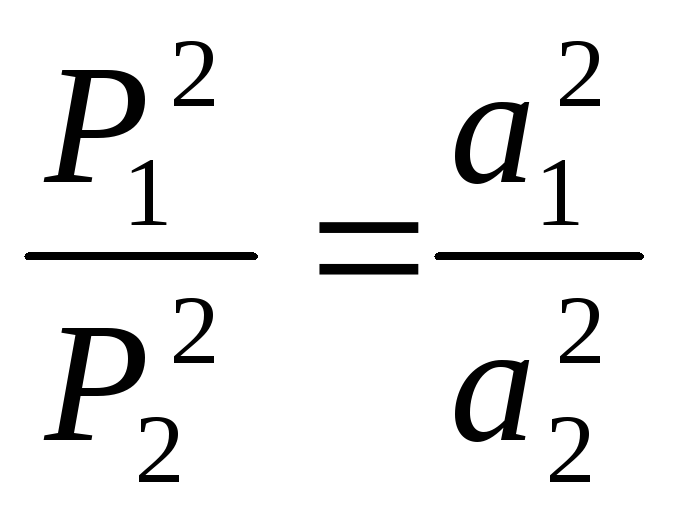
Соседние файлы в папке Лекции

• #
• #
• #
• #
• #

Большая полуось — это один из основных геометрических параметров объектов, образованных посредством конического сечения.

[править] Эллипс

Большой осью эллипса называется его наибольший диаметр, прямая проходящая через центр и два фокуса. А большая полуось составляет половину этого расстояния, и таким образом, идёт от центра, через фокус, и на край эллипса. А под углом в 90° к большой полуоси располагается малая полуось — это минимальное расстояние от центра эллипса до его края. Для частного случая круга, большая и малая полуоси равны и являются радиусами. Таким образом, можно думать о большой и малой полуосях как о, своего рода, радиусах эллипса.

Длина большой полуоси связана с длиной малой полуоси через эксцентриситет и коническое сечение , следующим образом:

Большая полуось представляет собой среднее значение наибольшего и наименьшего расстояния от точки эллипса до его фокусов. Рассмотрим теперь уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

Получим средние значения и и большую полуось

[править] Парабола

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в назад, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .

[править] Гипербола

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

.

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.^[1]

[править] Астрономия

[править] Орбитальный период

В небесной механике орбитальный период обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

где:

— это размер большой полуоси орбиты

— это стандартный гравитационный параметр (en:standard gravitational parameter)

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

В астрономии большая полуось, наряду с орбитальным периодом, является одним из самых важных орбитальных элементов орбиты космического тела .

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

где:

— орбитальный период в годах;

— большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

где:

— гравитационная постоянная

— масса центрального тела

— масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля-Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384400 км. В то время как расстояние до Луны относительно центра масс системы Земля-Луна составляет 379700 км, из-за влияния массы Луны центр масс находится не в центре Земли, а в 4700 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли 0,012 км/с. А общая сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; тоже самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

[править] Среднее расстояние

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения – в зависимости от величины, по которой производят усреднение:

• усреднение по эксцентрической аномалии. В таком случае среднее расстояние будет точно равно большой полуоси орбиты.
• усреднение по истинной аномалии, тогда среднее расстояние будет точно равно малой полуоси орбиты.
• усреднение по средней аномалии даст значение среднего расстояния, усреднённое по времени:

• усреднение по радиусу, которое получают из следующего соотношения:

[править] Энергия; расчёт большой полуоси методом векторов состояния

В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:

для эллиптических орбит

для гиперболической траектории

и

(en:specific orbital energy)

и

(стандартный гравитационный параметр), где:

— орбитальная скорость спутника, на основе вектора скорости,

— вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца),

— гравитационная постоянная,

и — массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.

[править] См. также

• Средняя аномалия
• Аргумент перицентра
• Эксцентриситет
• Наклон орбиты
• Долгота восходящего узла
• Перицентр
• Апоцентр

[править] Примечания

[править] Ссылки

• Semi-major and semi-minor axes of an ellipse With interactive animation

п·о·р Орбиты

Типы Основные Box-орбита • Орбита захвата • Эллиптическая орбита / Высокая эллиптическая орбита • Орбита ухода • Орбита захоронения • Гиперболическая траектория • Наклонная орбита / Ненаклонная орбита • Оскулирующая орбита  • Параболическая траектория  • Опорная орбита (в т.ч. низкая) • Синхронная орбита • (Полусинхронная • Субсинхронная)  • Стационарная орбита Геоцентрические Геосинхронная орбита • Геостационарная орбита • Солнечно-синхронная орбита • Низкая околоземная орбита • Средняя околоземная орбита • Высокая околоземная орбита • Молния-орбита • Околоэкваториальная орбита • Орбита Луны • Полярная орбита • Тундра-орбита • TLE Вокруг других небесных тел и точек Ареосинхронная орбита • Ареостационарная орбита • Гало-орбита • Орбита Лиссажу • Окололунная орбита • Гелиоцентрическая орбита • Солнечно-синхронная орбита Параметры Классические  Наклонение ·  Долгота восходящего узла ·  Эксцентриситет ·  Аргумент перицентра ·  Большая полуось ·  Средняя аномалия на эпоху Другие  Истинная аномалия ·  Малая полуось ·  Эксцентрическая аномалия ·  Средняя долгота ·  Истинная долгота ·  Период обращения Орбитальные манёвры Биэллиптическая переходная орбита · Запас характеристической скорости · Геопереходная орбита · Гравитационный манёвр · Гравитационный поворот · Орбита Гомана-Ветчинкина · Низкозатратная переходная траектория · Эффект Оберта · Изменение наклонения орбиты · Фазирование орбиты · Стыковка · Transposition, docking, and extraction · Манёвр увода Другие темы астродинамики Система небесных координат · Экваториальная система координат · Эпоха · Эфемерида · Законы Кеплера · Гравитационная задача N тел · Точки Лагранжа · Пертурбация · Межпланетная транспортная сеть Уравнение орбиты · Апоцентр и перицентр · Орбитальная скорость · Орбитальные векторы состояния · Специальная орбитальная энергия · Специальный относительный вращательный момент · Прямое движение · Ретроградное движение · Трасса орбиты

Небесная механика
Законы и задачи	Законы Ньютона | Закон всемирного тяготения | Законы Кеплера | Задача двух тел | Задача трёх тел | Гравитационная задача N тел | Задача Бертрана | Уравнение Кеплера
Небесная сфера	Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая | Международная небесная система координат | Сферическая система координат | Ось мира | Небесный экватор | Прямое восхождение | Склонение | Эклиптика | Равноденствие | Солнцестояние | Фундаментальная плоскость
Параметры орбит	Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра | Апоцентр и перицентр | Орбитальная скорость | Узел орбиты | Эпоха
Движение небесных тел	Движение Солнца и планет по небесной сфере | Эфемериды | Конфигурации планет: противостояние • квадратура • парад планет| Кульминация | Сидерический период | Орбитальный резонанс | Период вращения | Предварение равноденствий | Синодический период | Сближение | Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл | Покрытие | Прохождение | Либрация | Элонгация | Эффект Козаи | Эффект Ярковского | Эффект Джанибекова
Астродинамика
Космический полёт	Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая | Формула Циолковского | Гравитационный манёвр | Гомановская траектория | Метод оскулирующих элементов | Приливное ускорение| Изменение наклонения орбиты | Стыковка | Точки Лагранжа | Эффект «Пионера»
Орбиты КА	Геостационарная орбита | Гелиоцентрическая орбита | Геосинхронная орбита | Геоцентрическая орбита | Геопереходная орбита | Низкая опорная орбита | Полярная орбита | Тундра-орбита | Солнечно-синхронная орбита | Молния-орбита | Оскулирующая орбита

Мы знаем, что путь спутника, вращающегося вокруг Земли, известен как орбита . Этот путь может быть представлен с помощью математических обозначений. Орбитальная механика – это исследование движения спутников, присутствующих на орбитах. Таким образом, мы можем легко понять космические операции со знанием орбитального движения.

Орбитальные Элементы

Орбитальные элементы – это параметры, которые полезны для описания орбитального движения спутников. Ниже приведены орбитальные элементы .

• Большая полуось
• эксцентричность
• Средняя аномалия
• Аргумент перигея
• наклонение
• Прямое восхождение на восходящий узел

Вышеупомянутые шесть орбитальных элементов определяют орбиту земных спутников. Следовательно, легко отличить один спутник от других спутников на основе значений орбитальных элементов.

Большая полуось

Длина большой полуоси (а) определяет размер орбиты спутника. Это половина большой оси. Это проходит от центра через фокус к краю эллипса. Таким образом, это радиус орбиты в двух самых удаленных точках орбиты.

Обе полуоси и полуоси представлены на рисунке выше. Длина большой полуоси (а) определяет не только размер орбиты спутника, но и период обращения.

Если круговая орбита рассматривается как особый случай, то длина большой полуоси будет равна радиусу этой круговой орбиты.

эксцентричность

Значение эксцентриситета (e) фиксирует форму орбиты спутника. Этот параметр указывает на отклонение формы орбиты от идеального круга.

Если длины большой полуоси и малой оси эллиптической орбиты являются a & b, то математическое выражение для эксцентриситета (e) будет

$$ e = frac { sqrt {a ^ 2 – b ^ 2}} {a} $$

Значение эксцентриситета круговой орбиты равно нулю , так как оба a и b равны. Принимая во внимание, что значение эксцентриситета эллиптической орбиты лежит между нулем и единицей.

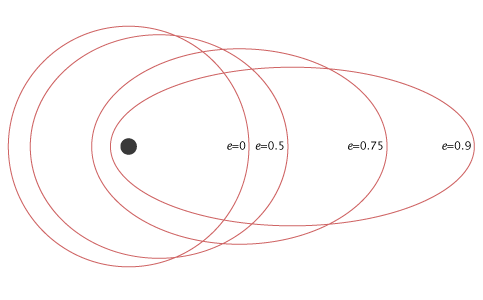
На следующем рисунке показаны различные спутниковые орбиты для разных значений эксцентриситета (e).

На приведенном выше рисунке спутниковая орбита, соответствующая нулевому значению эксцентриситета (e), является круговой орбитой. И остальные три спутниковые орбиты имеют эллиптическую форму, соответствующую значениям эксцентриситета (e) 0,5, 0,75 и 0,9.

Средняя аномалия

Для спутника точка, ближайшая к Земле, называется Перигеем. Средняя аномалия (М) дает среднее значение углового положения спутника относительно перигея.

Если орбита круглая, то средняя аномалия дает угловое положение спутника на орбите. Но если орбита эллиптическая, то вычисление точного положения очень сложно. В это время средняя аномалия используется в качестве промежуточного шага.

Аргумент Перигея

Спутниковая орбита разрезает экваториальную плоскость в двух точках. Первая точка называется нисходящим узлом , где спутник проходит от северного полушария к южному полушарию. Вторая точка называется восходящим узлом , где спутник проходит от южного полушария к северному полушарию.

Аргумент перигея (ω) – угол между восходящим узлом и перигеем. Если и перигей, и восходящий узел существуют в одной и той же точке, то аргумент перигея будет равен нулю

Аргумент перигея измеряется в плоскости орбиты в центре Земли в направлении движения спутника.

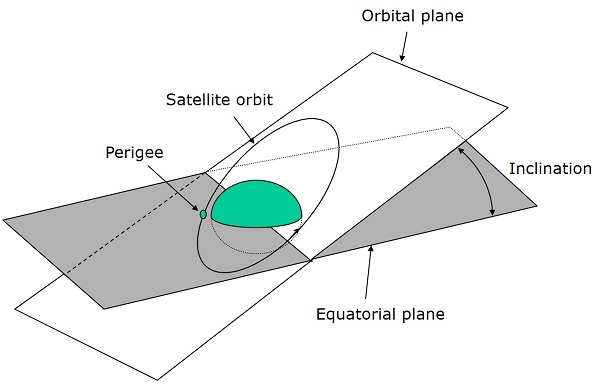
наклонение

Угол между плоскостью орбиты и экваториальной плоскостью Земли известен как наклон (i) . Он измеряется в восходящем узле с направлением с востока на север. Таким образом, наклон определяет ориентацию орбиты, рассматривая экватор Земли в качестве ориентира.

Есть четыре типа орбит, основанных на угле наклона.

• Экваториальная орбита – угол наклона равен нулю или 180 градусам.

• Полярная орбита – угол наклона 90 градусов.

• Поворотная орбита – Угол наклона лежит от нуля до 90 градусов.

• Ретроградная орбита – угол наклона составляет от 90 до 180 градусов.

Экваториальная орбита – угол наклона равен нулю или 180 градусам.

Полярная орбита – угол наклона 90 градусов.

Поворотная орбита – Угол наклона лежит от нуля до 90 градусов.

Ретроградная орбита – угол наклона составляет от 90 до 180 градусов.

Прямое Вознесение Восходящего Узла

Мы знаем, что восходящий узел – это точка, где спутник пересекает экваториальную плоскость при переходе от южного полушария к северному полушарию.

Прямое восхождение восходящего узла (Ω) – это угол между линией Овна и восходящим узлом в восточном направлении в экваториальной плоскости. Овен также называют весенним и равноденственным.

Наземный трек спутника – это путь на поверхности Земли, которая лежит точно под его орбитой. Наземный трек спутника может принимать различные формы в зависимости от значений орбитальных элементов.

Орбитальные уравнения

В этом разделе мы обсудим уравнения, связанные с орбитальным движением.

Силы, действующие на спутник

Спутник, когда он вращается вокруг Земли, подвергается притягивающей силе от Земли из-за гравитационной силы Земли. Эта сила известна как центростремительная сила (F ₁ ), потому что эта сила стремится к спутнику к нему.

Математически центростремительная сила (F ₁ ), действующая на спутник из-за земли, может быть записана как

$$ F_ {1} = frac {GMm} {R ^ 2} $$

Куда,

• G – универсальная гравитационная постоянная, и она равна 6,673 x 10 ^-11 Н ∙ м ² / кг ² .

• М – масса земли, и она равна 5,98 х 10 ²⁴ кг.

• м – масса спутника.

• R – расстояние от спутника до центра Земли.

G – универсальная гравитационная постоянная, и она равна 6,673 x 10 ^-11 Н ∙ м ² / кг ² .

М – масса земли, и она равна 5,98 х 10 ²⁴ кг.

м – масса спутника.

R – расстояние от спутника до центра Земли.

Спутник, когда он вращается вокруг Земли, подвергается воздействию силы притяжения Солнца и Луны из-за их гравитационных сил. Эта сила известна как центробежная сила (F ₂ ), потому что эта сила уводит спутник от земли.

Математически, центробежная сила (F ₂ ), действующая на спутник, может быть записана как

$$ F_ {2} = frac {mv ^ 2} {R} $$

Где v – орбитальная скорость спутника.

Орбитальная скорость

Орбитальная скорость спутника – это скорость, с которой спутник вращается вокруг Земли. Спутник не отклоняется от своей орбиты и движется с определенной скоростью на этой орбите, когда центростремительные и центробежные силы уравновешивают друг друга.

Итак, приравниваем центростремительную силу (F ₁ ) и центробежную силу (F ₂ ).

$$ frac {GMm} {R ^ 2} = frac {mv ^ 2} {R} $$

$$ => frac {GM} {R} = v ^ 2 $$

$$ => v = sqrt { frac {GM} {R}} $$

Следовательно, орбитальная скорость спутника равна

$$ v = sqrt { frac {GM} {R}} $$

Куда,

• G – гравитационная постоянная, и она равна 6,673 x 10 ^-11 Н ∙ м ² / кг ² .

• М – масса земли, и она равна 5,98 х 10 ²⁴ кг.

• R – расстояние от спутника до центра Земли.

G – гравитационная постоянная, и она равна 6,673 x 10 ^-11 Н ∙ м ² / кг ² .

М – масса земли, и она равна 5,98 х 10 ²⁴ кг.

R – расстояние от спутника до центра Земли.

Таким образом, орбитальная скорость в основном зависит от расстояния от спутника до центра Земли (R), поскольку G & M являются постоянными.