Как найти большую производную функции - Исправление недочетов и поиск решений вместе с Examum.ru

Пусть
функция
дифференцируема в некотором интервале.
Тогда её производная
,
вообще говоря, зависит отх
, то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.

Определение.
Производная
от первой производной называется
производной
второго порядка или второй производной
и обозначается символом
или,
то есть

Пример
1. Найти
вторую производную от функции
.

Решение. Найдем
первую производную функции:

Находим вторую
производную как производную первой
производной:

Определение.
Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом
или.

Определение.
Производной
n-ого
порядка функции

называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
или:

Определение.
Производные
порядка выше первого называются
высшими
производными.

Пример
2. Найти
производную четвертого порядка функции
.

Решение. Находим
последовательно первую, вторую, третью
и четвертую производные:

,,.

Пример
3.Найти
производную n-ого
порядка для функции
(k—const).

Решение. Имеем:

,,.

Пример
4. Найти
производную n-ого
порядка для функции
.

Решение. Имеем:

Замечание.
Аналогично можно получить формулу n-ой
производной функции
:

Пример
5. Найти
производную n-ого
порядка для степенной функции
, гдеи— любое вещественное число.

Решение.
Дифференцируя последовательно, получим:

В
частном случае, когда
,
гдеm
– натуральное число, получим:

при.

Замечание.
При строгом выводе формулы для производной
n-ого
порядка следует применять метод
математической индукции.

Вторая
производная параметрически заданной
функции

Если
функция задана параметрически уравнениями
,
то для нахождения производной второго
порядка нужно продифференцировать
выражение для её первой производной,
как сложной функции независимой
переменной.

Так
как
,
то

и с учетом того,
что

получим

,
то есть

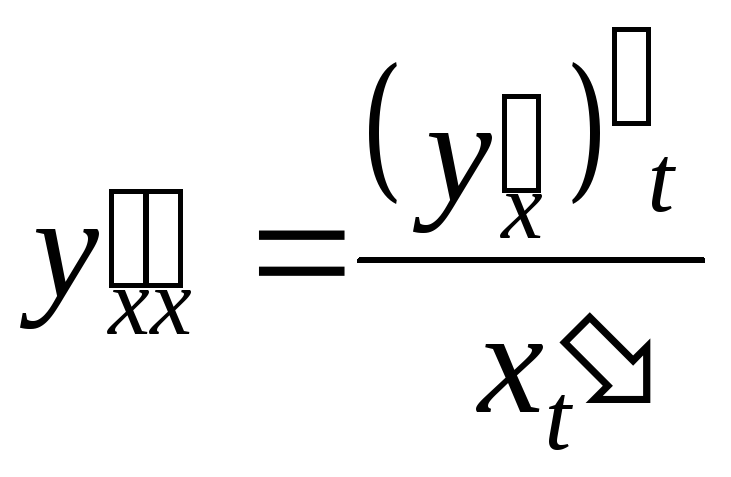
Аналогично можно найти третью
производную

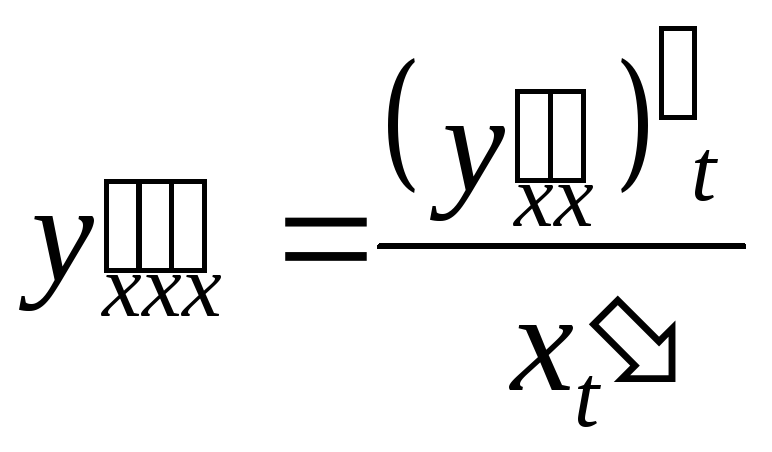
Пример
7. Найти
вторую производную параметрически
заданной функции
,.

Решение.,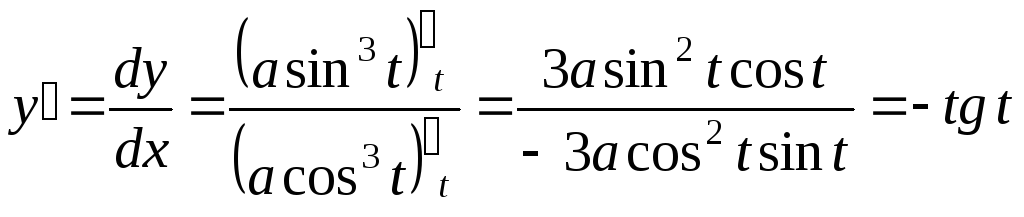

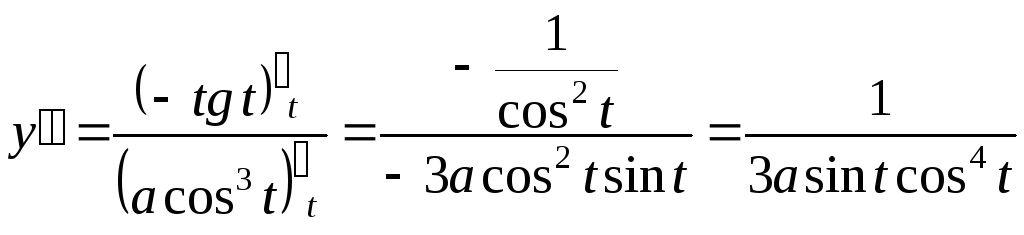
Формула Лейбница

Для
нахождения производной n-ого
порядка от произведения двух функций
большое практическое значение имеет
формула Лейбница.

Пусть
u
и
v
— некоторые
функции от переменной х,
имеющие производные любого порядка и
y=uv.
Выразим n-ую
производную
через производные функцийu
и
v.

Имеем последовательно

Легко подметить
аналогию между выражениями для второй
и третьей производных и разложением
бинома Ньютона соответственно во второй
и третьей степенях, но вместо показателей
степени стоят числа, определяющие
порядок производной, а сами функции
можно рассматривать как «производные
нулевого порядка». Учитывая это, получим
формулу Лейбница:

. (2)

Эту формулу
можно доказать методом математической
индукции.

Пример.
Найти пятую
производную функции
.

Решение.
Положим
и.
Найдем,,,,;.
Подставляя эти выражения в формулу
Лейбница при,
получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Производные высших порядков

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Дифференцируя производную первого порядка $f'(x)$, мы получим производную от производной — производную второго порядка. Производная от производной второго порядка называется производной третьего порядка, а производная $n$-го порядка называется производной от производной $n-1$-го порядка.

Производная второго порядка обозначается $y»$ или $f»(x)$. Таким образом, дифференцируя функцию $n$-раз, мы получим производную вида $f n(x)$.

Формула дифференцирования второго порядка имеет вид:

Производная n-го порядка равна нулю, если степень меньше порядка производной. Например, пятая производная функции $y = 5x^2$ равна нулю.

Пример 1

Найти вторую производную функции:

[y=xln (2x+1)]

Решение.

Найдем производную первого порядка сложной функции по формуле произведения:

[left[f(x)cdot g(x)right]{{‘} } =f(x)’cdot g(x)+f(x)cdot g(x)’]

[y’=left[xcdot ln (2x+1)right]{{‘} } =x’cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =1cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =]

[y’=ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =ln (2x+1)+xcdot frac{1}{2x+1} cdot (2x+1)’=]

[=ln (2x+1)+2xcdot frac{1}{2x+1} =ln (2x+1)+frac{2x}{2x+1} ]

Найдем производную второго порядка для выражения

[y»=left(ln (2x+1)+frac{2x}{2x+1} right){{‘} } =ln (2x+1)’+left(frac{2x}{2x+1} right){{‘} } =frac{1}{2x+1} cdot (2x+1)’+frac{2x’cdot (2x+1)-2xcdot (2x+1)’}{left(2x+1right)^{2} } =]

[y»=frac{2}{2x+1} +frac{2(2x+1)-2xcdot 2}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2((2x+1)-2x)}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2}{left(2x+1right)^{2} } =]

Упростим выражение

[y»=frac{2left(2x+1right)}{left(2x+1right)^{2} } +frac{2}{left(2x+1right)^{2} } =frac{2left(2x+1right)+2}{left(2x+1right)^{2} } =frac{4x+4}{left(2x+1right)^{2} } ]

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Пример 2

Найти производную четвертого порядка

[y=x^{5} -x^{4} +3x^{3} ]

Решение.

Найдем производную первого порядка

[y’=left(x^{5} -x^{4} +3x^{3} right){{‘} } =5x^{4} -4x^{3} +3cdot 3x^{2} =5x^{4} -4x^{3} +9x^{2} ]

Найдем производную второго порядка

[y»=left(5x^{4} -4x^{3} +9x^{2} right){{‘} } =20x^{3} -12x^{2} +18x]

Найдем производную третьего порядка

[y»’=left(20x^{3} -12x^{2} +18xright){{‘} } =60x^{2} -24x+18]

Найдем производную четвертого порядка

[y»»=left(60x^{2} -24x+18right){{‘} } =120x-24]

Пример 3

Найти производную четвертого порядка функции

[y=frac{x^{2} +5x^{3} }{18} ]

Решение: Самая большая степень составного неизвестного равна 3, что меньше степени производной, а значит, производная четвертого порядка равна 0.

Пример 4

Найти производную 13-го порядка функции

[y=sin x]

Решение.

Найдем производную первого порядка

[y’=sin’x=cos x=sin (x+frac{pi }{2} )]

Найдем производную второго порядка

[y»=cos’x=-sin x=sin (x+2frac{pi }{2} )]

Найдем производную третьего порядка

[y»’=-sin’x=-cos x=sin (x+3frac{pi }{2} )]

Найдем производную четвертого порядка

[y^{(4)} =-cos x’=sin x=sin (x+4frac{pi }{2} )]

Таким образом:

[y^{(n)} =sin (x+frac{ncdot pi }{2} ),nin N]

Найдем производную 13-го порядка:

[y^{(13)} =sin (x+frac{13cdot pi }{2} )=cos x]

«Производные высших порядков» 👇

Пример 5

Найти производную n-порядка функции

[y=frac{x}{1-x} ]

Решение.

Найдем производную первого порядка

[y’=left(frac{x}{1-x} right){{‘} } =frac{x'(1-x)-x(1-x)’}{(1-x)^{2} } =frac{1-x+x}{(1-x)^{2} } =frac{1}{(1-x)^{2} } =frac{1!}{(1-x)^{1+1} } ]

Найдем производную второго порядка

[y»=left(frac{1}{(1-x)^{2} } right){{‘} } =left((1-x)^{-2} right){{‘} } =-2(1-x)^{-3} (1-x)’=-2(1-x)^{-3} cdot (-1)=frac{2}{(1-x)^{3} } =frac{2!}{(1-x)^{2+1} } ]

Найдем производную 3 порядка

[y»’=left(frac{2}{(1-x)^{3} } right){{‘} } =2left((1-x)^{-3} right){{‘} } =2cdot left(-3right)(1-x)^{-4} (1-x)’=-6cdot (1-x)^{-4} cdot (-1)=frac{1cdot 2cdot 3}{(1-x)^{4} } =frac{3!}{(1-x)^{3+1} } ]

Выведем формулу производной $n$-порядка

[y^{(n)} =frac{n!}{(1-x)^{n+1} } ]

Пример 6

Найти значение второй производной в точке 1

[y=e^{2x-1} ]

Решение.

Найдем производную первого порядка

[y’=left(e^{2x-1} right){{‘} } =e^{2x-1} cdot 2]

Найдем производную второго порядка

[y»=left(2cdot e^{2x-1} right){{‘} } =2cdot e^{2x-1} cdot 2=4e^{2x-1} ]

Найдем производную в точке 1

[y»=4e^{2x-1} =4e^{2cdot 1-1} =4e]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 11.12.2022

Источник

Содержание:

Механический смысл второй производной
Вычисления производной любого порядка, формула Лейбница

Если функция $y=f(x)$ имеет производную в каждой точке
$x$ своей области определения, то ее производная
$f^{prime}(x)$ есть функция от
$x$. Функция
$y=f^{prime}(x)$, в свою очередь, может иметь производную, которую
называют производной второго порядка функции $y=f(x)$ (или второй
производной) и обозначают символом $f^{prime prime}(x)$. Таким образом

$f^{prime prime}(x)=frac{mathrm{d}^{2} y}{mathrm{d} x^{2}}=lim _{x rightarrow x_{0}} frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}$

Пример

Задание. Найти вторую производную функции $y(x)=x ln (2 x+3)$

Решение. Для начала найдем первую производную:

$y^{prime}(x)=(x ln (2 x+3))^{prime}=(x)^{prime} cdot ln (2 x+3)+x cdot(ln (2 x+3))^{prime}=$

$=1 cdot ln (2 x+3)+x cdot frac{1}{2 x+3} cdot(2 x+3)^{prime}=ln (2 x+3)+$

$+frac{x}{2 x+3} cdotleft[(2 x)^{prime}+(3)^{prime}right]=ln (2 x+3)+frac{x}{2 x+3} cdotleft[2 cdot(x)^{prime}+0right]=$

$=ln (2 x+3)+frac{x}{2 x+3} cdot 2 cdot 1=ln (2 x+3)+frac{2 x}{2 x+3}$

Для нахождения второй производной продифференцируем выражение для первой производной еще раз:

$y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(ln (2 x+3)+frac{2 x}{2 x+3}right)^{prime}=$

$=(ln (2 x+3))^{prime}+left(frac{2 x}{2 x+3}right)^{prime}=$

$=frac{1}{2 x+3} cdot(2 x+3)^{prime}+frac{(2 x)^{prime} cdot(2 x+3)-2 x cdot(2 x+3)^{prime}}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3}left[(2 x)^{prime}+(3)^{prime}right]+frac{2(x)^{prime} cdot(2 x+3)-2 x cdotleft[(2 x)^{prime}+(3)^{prime}right]}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3}left[2 cdot(x)^{prime}+0right]+frac{2 cdot 1 cdot(2 x+3)-2 x cdotleft[2 cdot(x)^{prime}+0right]}{(2 x+3)^{2}}=$

$=frac{1}{2 x+3} cdot 2 cdot 1+frac{2(2 x+3)-2 x cdot 2 cdot 1}{(2 x+3)^{2}}=$

$=frac{2}{2 x+3}+frac{4 x+6-4 x}{(2 x+3)^{2}}=frac{2}{2 x+3}+frac{6}{(2 x+3)^{2}}=$

$=frac{2(2 x+3)+6}{(2 x+3)^{2}}=frac{4 x+6+6}{(2 x+3)^{2}}=frac{4 x+12}{(2 x+3)^{2}}=frac{4(x+3)}{(2 x+3)^{2}}$

Ответ. $y^{prime prime}(x)=frac{4(x+3)}{(2 x+3)^{2}}$

Производные более высоких порядков определяются аналогично. То есть производная
$n$-го порядка функции
$f(x)$ есть первая производная от производной
$(n-1)$-го порядка этой функции:

$f^{(n)}(x)=frac{mathrm{d}^{n} y}{mathrm{d} x^{n}}=left(f^{(n-1)}(x)right)^{prime}$

Замечание

Число $n$, указывающее порядок производной, заключается в скобки.

Механический смысл второй производной

Теорема

(Механический смысл второй производной)

Если точка движется прямолинейно и задан закон ее движения $s=f(t)$,
то ускорение точки равно второй производной от пути по времени:

$a(t)=s^{prime prime}(t)$

Замечание

Ускорение материального тела равно первой производной от скорости, то есть:

$a(t)=v^{prime}(t)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Материальная точка движется по закону
$s(t)=2 t^{3}+3 t$, где
$s$ измеряется в метрах, а
$t$ — в секундах. Найти значение
$t$, при котором ускорение точки равно 12.

Решение. Найдем ускорение материальной точки:

$a(t)=s^{prime prime}(t)=left(2 t^{3}+3 tright)^{prime prime}=left(left(2 t^{3}+3 tright)^{prime}right)^{prime}=left(left(2 t^{3}right)^{prime}+(3 t)^{prime}right)^{prime}=$

$=left(2 cdot 3 t^{2}+3 cdot 1right)^{prime}=left(6 t^{2}+3right)^{prime}=left(6 t^{2}right)^{prime}+(3)^{prime}=$

$=6 cdotleft(t^{2}right)^{prime}+0=6 cdot 2 t=12 t$

Искомое время $t$ найдем из уравнения:

$a(t)=12 Rightarrow 12 t=12 Rightarrow t=1 mathrm{c}$

Ответ. $t=1 c$

Вычисления производной любого порядка, формула Лейбница

Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение
формулы вычисления производной от произведения двух функций, применяется формула Лейбница:

$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{prime}+C_{n}^{2} u^{(n-2)} v^{prime prime}+ldots+C_{n}^{n-1} u^{prime} v^{(n-1)}+u v^{(n)}$

где $C_{n}^{k}=frac{n !}{k !(n-k) !}$,
$n !=1 cdot 2 cdot ldots cdot n$ — факториал
натурального числа
$n$.

Пример

Задание. Найти $y^{(4)}(x)$, если
$y(x)=e^{4 x} sin 3 x$

Решение. Так как заданная функция представляет собой произведение двух функций
$u(x)=e^{4 x}$,
$v(x)=sin 3 x$, то для нахождения производной четвертого
порядка целесообразно будет применить формулу Лейбница:

$y^{(4)}(x)=left(e^{4 x}right)^{(4)} cdot sin 3 x+C_{4}^{1}left(e^{4 x}right)^{(3)} cdot(sin 3 x)^{prime}+$

$+C_{4}^{2}left(e^{4 x}right)^{prime prime} cdot(sin 3 x)^{prime prime}+C_{4}^{3}left(e^{4 x}right)^{prime} cdot(sin 3 x)^{(3)}+e^{4 x}(sin 3 x)^{(4)}$

Найдем все производные и посчитаем коэффициенты при слагаемых.

1) Посчитаем коэффициенты при слагаемых:

$C_{4}^{1}=frac{4 !}{1 ! cdot(4-1) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$

$C_{4}^{2}=frac{4 !}{2 ! cdot(4-2) !}=frac{4 !}{2 ! cdot 2 !}=frac{2 ! cdot 3 cdot 4}{2 ! cdot 2 !}=frac{3 cdot 4}{2}=6$

$C_{4}^{3}=frac{4 !}{3 ! cdot(4-3) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$

2) Найдем производные от функции $u(x)$:

$u(x)=e^{4 x}, u^{prime}(x)=left(e^{4 x}right)^{prime}=e^{4 x} cdot(4 x)^{prime}=e^{4 x} cdot 4 cdot(x)^{prime}=4 e^{4 x}$

$u^{prime prime}(x)=left(u^{prime}(x)right)^{prime}=left(4 e^{4 x}right)^{prime}=4 cdotleft(e^{4 x}right)^{prime}=16 e^{4 x}$

$u^{prime prime prime}(x)=left(u^{prime prime}(x)right)^{prime}=left(16 e^{4 x}right)^{prime}=64 e^{4 x}$

$u^{(4)}(x)=left(u^{prime prime prime}(x)right)^{prime}=left(64 e^{4 x}right)^{prime}=256 e^{4 x}$

3) Найдем производные от функции $v(x)$:

$v(x)=sin 3 x, v^{prime}(x)=(sin 3 x)^{prime}=cos 3 x cdot(3 x)^{prime}=3 cos 3 x$

$v^{prime prime}(x)=left(v^{prime}(x)right)^{prime}=(3 cos 3 x)^{prime}=3 cdot(cos 3 x)^{prime}=$

$=3 cdot(-sin 3 x) cdot(3 x)^{prime}=-9 sin 3 x$

$v^{prime prime prime}(x)=left(v^{prime prime}(x)right)^{prime}=-27 cos 3 x, v^{(4)}(x)=left(v^{prime prime prime}(x)right)^{prime}=81 sin 3 x$

Тогда

$y^{(4)}(x)=256 e^{4 x} cdot sin 3 x+4 cdot 64 e^{4 x} cdot 3 cos 3 x+$

$+6 cdot 16 e^{4 x} cdot(-9 sin 3 x)+4 cdot 4 e^{4 x} cdot(-27 cos 3 x)+e^{4 x} 81 sin 3 x=$

$=e^{4 x}(336 cos 3 x-527 sin 3 x)$

Ответ. $y^{(4)}(x)=e^{4 x}(336 cos 3 x-527 sin 3 x)$

Читать дальше: таблица производных высших порядков.

Источник

Под понятием производные различных порядков обычно понимаются производные первого или высших порядков.

Дифференцирование производной первого порядка [F^{prime}(x)] позволит вычислить производную от производной — именуемую производной второго порядка. Далее назовем определение производной.

Производная производной второго порядка именуется производной третьего порядка, в этой связи производная n-го
порядка определяется как производная от производной n-1го порядка.

Производная функции второго порядка обозначается записью [y^{prime prime}] или [F^{prime prime}(x)]. Дифференцировка функции [n] раз приводит к получению производной вида [f n(x)].

Дифференцирование второго порядка

Производные в математике всегда находятся по определенной формуле. Итак, формула дифференцирования второго порядка записывается следующим образом:

[f^{prime prime}(x)=frac{d^{2} y}{d x^{2}}=lim _{x rightarrow x_{0}}=frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}]

В случае, если степень меньше, чем порядок производной, производная n-го порядка будет равна нулю.

Таблица с формулами производных высших порядков

Формулы для нахождения производных высших порядков наиболее удобно представить в виде таблицы формул производных:

Функция	Формула нахождения
[left(x^{p}right)^{(n)}]	[left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}]
[left(a^{k x+b}right)^{(n)}]	[left(a^{k x+b}right)^{(n)}=k^{n} a^{k x+b} 1 n^{n} a]
[left(e^{k x+b}right)^{(n)}]	[left(e^{k x+b}right)^{(n)}=k^{n} e^{k x+b}]
[(sin a x)^{(n)}]	[(sin a x)^{(n)}=a^{n} sin left(a x+frac{п n}{2}right)]
[(cos a x)^{(n)}]	[(sin a x)^{(n)}=a^{n} cos left(a x+frac{п n}{2}right)]
[left((a x+b)^{p}right)^{n}]	[left((a x+b)^{p}right)^{n}=a^{n} p(p-1)(p-2) ldots(p-n+1)(a x+b)^{n-1}]
[left(log _{a}\|x\|right)^{(n)}]	[left(log _{a}\|x\|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n} ln a}]
[(ln \|x\|)^{n}]	[left(log _{a}\|x\|right)^{(n)}=frac{(-1)^{n-1}(n-1) !}{x^{n}}]
[(a u(x)+beta gamma(x))^{n}]	[(a u(x)+beta gamma(x))^{n}=a u^{n}(x)+beta^{n} gamma(x)]

Нет времени решать самому?

Наши эксперты помогут!

Примеры нахождения производных

Примеры

Пример 1

Как найти производную первого порядка функции по формуле произведения:

[|f(x) cdot g(x)|^{prime}=f(x)^{prime} cdot g(x)+f(x) cdot g(x)^{prime}\y^{prime}=[x cdot ln (2
x+1)]^{prime}=x^{prime} cdot ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=1 cdot ln (2 x+1)+x cdot(ln
(2 x+1))^{prime}=y^{prime}\=ln (2 x+1)+x cdot(ln (2 x+1))^{prime}\=ln (2 x+1)+x frac{1}{2 x+1}
cdot(2 x+1)^{prime}=ln (2 x+1)+2 x cdot frac{1}{2 x+1}\=ln (2 x+1)+frac{2 x}{2 x+1}]

Как найти производную второго порядка в данном выражении:

[y^{prime prime}=left(ln (2 x+1)+frac{2 x}{2 x+1}right)^{prime}=ln (2 x+1)^{prime}+left(frac{2
x}{2 x+1}right)^{prime}\=left(frac{1}{2 x+1}right) cdot(2 x+1)^{prime}+frac{2 x^{prime} cdot(2
x+1)-2 x cdot(2 x+1)^{prime}}{(2 x+1)^{2}}\=y^{prime prime}=frac{2}{2 x+1}+frac{2(2 x+1)-2 x cdot
2}{(2 x+1)^{2}}=frac{2}{2 x+1}+frac{2((2 x+1)-2 x)}{(2 x+1)^{2}}\=frac{2}{2 x+1}+frac{2}{(2
x+1)^{2}}]

Упростим полученное решение:

[y^{prime prime}=frac{2(2 x+1)}{(2 x+1)^{2}}+frac{2}{(2 x+1)^{2}}=frac{2(2 x+1)+2}{(2 x+1)^{2}}=frac{4
x+4}{(2 x+1)^{2}}]

Пример 2

Задача на нахождение производной различных порядков на примере производной четвертого порядка:
[y=x^{5}-x^{4}+3 x^{3}]

Решение:

[y^{prime}=left(x^{5}-x^{4}+3 x^{3}right)^{prime}=5 x^{4}-4 x^{3}+3 cdot 3 x^{2}=5 x^{4}-4 x^{3}+9
x^{2}\y^{prime prime}=left(5 x^{4}-4 x^{3}+9 x^{2}right)^{prime}=20 x^{3}-12 x^{2}+18 x\y^{prime
prime prime}=left(20 x^{3}-12 x^{2}+18 xright)^{prime}=60 x^{2}-24 x+18\y^{4}=left(60 x^{2}-24
x+18right)^{prime}=120 x-24]

Пример 3

Нахождение производной различных порядков от функций на следующем частном примере:

[y=frac{x^{2}+5 x^{3}}{18}]

Ответ: решение не является сложным и не потребует онлайн-калькулятора. Наибольшая степень одной из переменных
равна 3, что меньше степени производной. Следовательно, производная четвертого порядка равна 0.

Пример 4

Необходимо найти производную 13 порядка для [y=sin x]

Решение: найдем производную первого порядка (и затем 2-4 порядков)

[y^{prime}=sin ^{prime} x=cos x=sin left(x+frac{pi}{2}right)\y^{prime prime}=cos ^{prime}
x=-sin x=sin left(x+2 frac{pi}{2}right)\y^{prime prime prime}=-sin ^{prime} x=-cos x=sin
left(x+3 frac{pi}{2}right)\y^{(4)}=-cos ^{prime} x=sin x=sin left(x+4 frac{pi}{2}right)]

Следовательно:

[y^{(n)} sin left(x+frac{n cdot pi}{2}right), n in N]

Итоговый результат:

[y^{(13)}=sin left(x+frac{13 cdot pi}{2}right)=cos x]

Пример 5

Подсчитайте производную четвертой степени функции [x^{8}]

Решение:

Используем формулу нахождения производной высшего порядка

[left(x^{p}right)^{(n)}=p(p-1)(p-1) ldots(p-n+1) x^{p-n}]

Учтем, что p=8, n=4

[left(x^{8}right)^{(4)}=8(8-1)(8-2)(8-4+1) x^{8-4}=8 cdot 7 cdot 6 cdot 5 cdot x^{4}=1680 x^{4}\left(x^{8}right)^{(4)}=1680 x^{4}]

Пример 6

Подсчитайте производную функции [y=2^{x}-operatorname{arctg} x].

Решение:

[y^{prime}=left(2^{x}-operatorname{arctg} xright)^{prime}=left(2^{x}right)^{prime}-(operatorname{arctg} x)^{prime}]

Используем формулы для обратной и тригонометрической функции [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]

Ответ: [y^{prime}=2^{x} ln 2-frac{1}{1+x^{2}}]

Источник

Содержание:

Производные высших порядков
Производные высших порядков с примерами
Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически

Производные высших порядков

Производная функции у = f (x) является также функцией: у’= f’ (x).

Эта функция также может иметь производную. Эта новая производная называется второй производной функции у = f (x) или производной функции f (x) второго порядка и обозначается или .
Производная второй производной, то есть функции называется третьей производной или производной третьего порядка и обозначается символом или . Так можно ввести производные четвертого, пятого и вообще n-го порядка, которые обозначают .

Пример 1. Найти производную четвертого порядка функции .

Решение. Имеем:

Пример 2. Найти производные n-го порядка от функций
а) y = e^x, б) y = sin x, в) y = cos x.
Решение.
а)
б)

и по индукции
в) аналогично находим

Производные высших порядков с примерами

Пусть функция имеет производную во всех точках некоторой окрестности точки Если функция в свою очередь имеет в точке производную то она называется второй производной функции в точке и обозначается или Таким образом, опуская обозначения аргумента, имеем

Аналогично определяются и производные более высоких порядков

где для удобства считается, что

Примеры:

1. Если то вообще, В частности, если то

2. Если Заметив, что получим

Вообще,

Аналогично,

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 1. Если функции имеют в точке производные порядка то любая их линейная комбинация и их произведение имеют в точке производные порядка причем

Все производные в формулах (11.5) и (11.6) берутся в точке биномиальные коэффициенты.

Символическая запись означает, что это выражение (см. среднюю часть формулы (11.6)) по своей структуре напоминает формулу бинома Ньютона

только вместо степеней берутся производные соответствующих порядков функций Формула (11.6) называется формулой Лейбница*).

Докажем формулы (11.5) и (11.6) методом математической индукции. В п. 10.5 формула (11.5) была доказана для

Пусть справедлива формула (11.5); покажем, что тогда будет справедлива и аналогичная формула для производной порядка

Формула (11.5) доказана; докажем формулу (11.6).

Возможно вам будут полезны данные страницы:

Пусть справедлива формула (11.6) для производной порядка от произведения функций. Докажем, что тогда будет справедлива и аналогичная формула для производной порядка

Вспомнив, что (см. п. 2.4)

получим

Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически

С помощью формулы производной сложной функции (см. п. 10.7) можно вычислять и производные высших порядков сложной функции. Пусть функция дважды дифференцируема в точке функция дважды дифференцируема в точке и имеет смысл сложная функция Вычислим вторую производную сложной функции (для простоты записи аргумент писать не будем):

Аналогично вычисляются и производные более высоких порядков. С помощью формул производных обратной функции (см. п. 10.6) и сложной функции (см. п. 10.7) можно вычислять производные высших порядков обратных функций. Вычислим, например, вторую производную. Пусть функция дважды дифференцируема в точке в ее окрестности непрерывна и строго монотонна, причем Тогда для второй производной имеем в точке