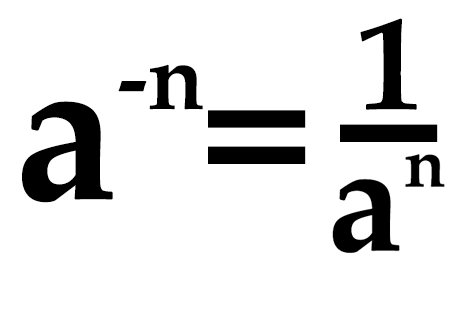Как найти большую степень большого числа - Исправление недочетов и поиск решений вместе с Examum.ru

Большую степень не вычисляют в лоб, тем более, что при выполнении действий в модульной арифметике её не нужно хранить целиком, достаточно хранить остаток от деления на известное постоянное число. Знак «тождественное равенство» используется как знак равенства в модульной арифметике, если модуль указан отдельно, поскольку сами числа, естественно, не равны.

Дискретное логарифмирование — формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.

Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b — произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) — неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.

Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат — 1, 1, 1, 1, 75, 75*215 mod 541 = 436.

Источник

Как вычислить большую степень?

Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.

2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.

Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.

Какие подходы задействованы для вычисления:
а) большой степени
б) откуда взялось деление с остатком?
в) не понял суть знака «тождественно равно» (вики прочитал, но разницы от обычного знака равенства не уяснил)

Вопрос задан более трёх лет назад
5101 просмотр

Facebook
Вконтакте
Twitter

Как посчитать число в большой степени

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень – это вычисление значения степени некоторого числа.

То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите – 2 в степень 4 .

Решение

Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1

0 0 – не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 2 в степень – 3 .

Решение

Используя определение выше, запишем: 2 – 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень – 2 .

Решение

Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: ( 1 , 43 ) – 2 = 10000 20449

Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 – 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2

После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Вычислите приближенное значение 21 , 174367 .

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .

Онлайн калькулятор разложения Шенкса (задача дискретного логарифмирования) выдал подобные результаты.

2^(1⋅24) ≡ 265(mod541)
2^(2⋅24) ≡ 436(mod541)
.

Заранее могу сказать, что посчитал он правильно, однако сам способ вычисления я совершенно не понял.

Вопрос задан более года назад
602 просмотра

Дискретное логарифмирование – формально, задача на пространстве решений, на котором можно применять модульную арифметику над многочленами или числами, с некоторым простым числом в качестве размера множества, частного для деления по модулю и вообще.

Саму степень по модулю можно вычислить довольно простым образом: Вначале раскладываем показатель на двоичные составляющие: 2*24 = 48 = 32+16 = 2^5+2^4. Потом пользуемся двумя тождествами: Первое x^(a+b)=x^a*x^b – произведение степеней одного числа равно степени числа в сумме показателей (забыл точное название). Второе (x*y) mod n = (x mod n)*(y mod n) – неважно, когда брать остаток, в начале или в конце. В итоге возведение числа 2 в большую степень по модулю N выполняется так: в результат заносится 1, в аргумент 2, потом в цикле по разрядам показателя если текущий двоичный разряд показателя 1, результат множится на аргумент и берется остаток по модулю N, который кладется в результат, а аргумент потом умножается на себя и остаток аргумента по модулю N кладется в аргумент.

Итого: аргумент принимает последовательно значения 2, 4, 16, 256, 65536 mod 541 = 75, 75*75 mod 541 = 215, а результат – 1, 1, 1, 1, 75, 75*215 mod 541 = 436.

Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.

Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».

Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.

Как возвести число в степень.

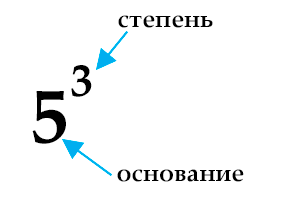
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:

Возведение в степень

А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.

5 3 = 5 x 5 x 5 = 125

Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.

Как возводить в отрицательную степень.

При возведении в отрицательную степень необходимо использовать простое правило:

как возводить в отрицательную степень

Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2 -3

Возвести в степень (по модулю) + большие числа

Алгоритм быстрого возведения в степень онлайн с решением по модулю и без модуля. Функциональность поддерживает работу с большими числами.

Использование:

alt=»✔» />Заполняем необходимые данные целыми числами, отвечая на вопросы формы.
alt=»✔» />Жмем кнопку вычислить и получаем результат.

alt=»ℹ» />Галочка «по модулю» позволяет указать модуль, по которому необходимо возводить в степень.
alt=»ℹ» />Галочка «с решением» позволяет получить этапы вычисления: каким образом число возводилось в степень.

Ограничения калькулятора:

Максимальное число, которое можно возвести в степень — 1 000 000.
Максимальная степень, в которую можно возвести — 5000.
Модуль может быть довольно-таки большим, до 100 символов в числе. [1; 10e100)

Алгоритм быстрого возведения в степень (по модулю).

Одним из основных действий арифметики вычетов, возникающих, например, в криптографии, является вычисление а х (mod m), то есть нахождение такого у, что

где a, x, m — натуральные числа. Далее считаем, что a < m. Запись у = b (mod m) означает, что у ≡ b (mod m) и 0 ≤ у < m, т.е, y — наименьший неотрицательный вычет по модулю m, лежащий в том классе, что и b.

Если вычислять «в лоб», т.е. последовательно находить (приводим формулы по модулю):

то нужно выполнить (x — 1) умножение в кольце Z_m, Если n — количество разрядов в двоичной записи х, то число умножений не меньше, чем 2 n-1.

Лемма 1: Пусть x, m, a ∈ N. Пусть x = (x₀x₁ … x_n-1)₂ т.е.

Определим целые а_j по реккурентным формулам

Алгоритм (быстрого возведения в степень). Даны натуральные a, m и x = (x_n-1x_n-2 … x₀)₂. Нужно вычислить y = a x (mod m),

1. Вычисляем a_j (0 ≤ j ≤ n — 1) по формулам (2),

Лемма 2. Пусть n — число разрядов в двоичной записи x. Тогда, приведенный выше алгоритм требует выполнения не более, чем, 2(n -1) умножений в кольце Z_m

Пример 1. Возведем число 2 50 без модуля.

50₁₀ = 110010₂ , считаем длину в двоичной записи n = 6. Следовательно, нам надо посчитать a₁ … a₆ по формулам 2 из теории.

a₁ = 2; a₂ = 2 2 = 4, a₃ = 4 2 = 16, a₄ = 16 2 = 256, a₅ = 256 2 = 65536, a₆ = 65536 2 = 4294967296

x₁ = 0, x₂ = 1, x₃ = 0, x₄ = 0, x₅ = 1, x₆ = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).

Перемножаем a_i-ые по второй формуле пункта 2. Другими словами, перемножаем между собой те a_i-ые, у которых на соответствующей позиции в двоичной записи степени стоят единицы — это a₂, a₅ и a₆;

2 50 = 4 * 65536 * 4294967296 = 1125899906842624

Пример 2. Возведем число 2 50 по модулю 100. Все аналогично, только считаем a_i-ые и произведения a_i-ых по модулю 100.

a₁ = 2; a₂ = 2 2 = 4, a₃ = 4 2 = 16, a₄ = 16 2 = 56, a₅ = 56 2 = 36, a₆ = 36 2 = 96 по модулю 100

x₁ = 0, x₂ = 1, x₃ = 0, x₄ = 0, x₅ = 1, x₆ = 1 — двоичная запись в обратном порядке (от младших разрядов к старшим).

2 50 = 4 * 36 * 96 = 24 по модулю 100.

Заметили неточность в работе калькулятора? Убедительная просьба сообщить об этом в комментариях или через форму обратной связи. Заранее Вас благодарим.

Источник

Как возвести в большую степень

Самое обыкновенное возведение числа в степень нередко вызывает сложности у программ и калькуляторов, если значение степени достаточно велико. Существует несколько приемов, необходимых для того, чтобы заставить калькулятор посчитать правильный результат.

Вам понадобится

компьютер
программа-калькулятор

Инструкция

Откройте программу-калькулятор на вашем компьютере. Введите число A, которое нужно возвести в большую степень N. Попробуйте произвести возведение в степень. В большинстве случаев программа-калькулятор успешно справится с заданием и выдаст результат на экран. Однако, прямой метод не всегда срабатывает. Программы-калькуляторы часто написаны не самым лучшим образом и могут не справляться с рядом простых с виду задач. Именно к таким задачам относится возведение в большую степень. Например, для значения N = 10000000000 калькулятор Windows отказывается считать результат, а калькулятор Ubuntu просто зависает.

Разложите показатель степени N на несколько множителей, каждый из которых не превышает по значению 100000. С таким показателем большинство калькуляторов успешно справится. Если один из множителей окажется дробным числом, ничего страшного. Например, показатель степени 333333333 можно разложить на множители 100000 и 3333,33333.

Согласно формуле A^(N1*N2) = (A^N1)^N2 последовательно возведите основание А в степени, равные полученным на предыдущем шаге множителям. Например, сначала возведите число А в степень 100000, а затем получившийся результат возведите в степень 3333,33333. После этих расчетов вы получите необходимый вам результат.

Видео по теме

Обратите внимание

Если один из множителей получился дробным, а основание степени является отрицательным числом, программа-калькулятор не позволит вам произвести возведение отрицательного числа в дробную степень. В этом случае возводите модуль основания в нужную вам степень, а потом, если потребуется, измените знак результата. Результат должен быть отрицательным, если степень является нечетным числом.

Полезный совет

Если значение А близко к единице, а N очень велико, воспользуйтесь формулой (1 + 1/A)^N -> e. Например, 1,000005^200000 приблизительно равняется числу е.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Возведение в степень по модулю — в кольце
§ 4. Приближенное вычисление иррациональных чисел
экспонентов, правила, которые дадут вам большую власть над числами
Обретение Высшей Силы – 5 практических способов повысить духовное осознание
- Бог и двенадцать шагов
- Наука и духовность
- Как мне может помочь Высшая Сила??
- Как найти высшую силу?
  - 1 – Будьте открытыми
  - 2 — Медитация
  - 3 – Молитесь
  - 4 -Помогайте людям
  - 5 – Продолжайте искать

Возведение в степень по модулю — в кольце

Модульная алгебра — это довольно важный раздел, касательно информационной безопасность, а именно криптографии. И не смотря что курс теории чисел и модульной арифметики на кафедре СИБ довольно хорош, многие не всегда могут вспомнить некоторые нюансы, которые в будущем могут облегчить жизнь. Более того, я увидел что в ВГУ также «увлекаются» криптографией, и RSA (http://fkn.ktu10.com/?q=node/4214) и так как при реализации нужно возводить число в очень большую степень а потом находить остаток от деления на другое (модуль) из-за чего приходится использовать либо слишком малые блоки либо работать с большими числами (http://fkn.ktu10.com/?q=node/4233).
В реальности, же, многие устройства реализуют ассиметричные блочные алгоритмы шифрования, и при этом они работают с полноценными блоками и часто не используют большие числа (не всегда это возможно).

О том как возвести число в очень большую степень в модульной арифметике и при этом не повесив комп, я сегодня расскажу.

{11}_{5} = [7]_{5} * [1]_{5} = [7]_{5} = [2]_{5}
$$

К сожалению пример не очень удачный, но короткий (быстро закончился, 1 в 11-й степени это 1), а так, в конце у нас может появиться к примеру такой вот список:
$$
[7]_{5} * [4]_{5} * [3]_{5} * [2]_{5} * [1]_{5} * [2]_{5}
$$
В этом случае их попарно перемножаем и каждый раз после умножения находим остаток, к примеру:
$[7]_{5} * [4]_{5} = [3]_{5} $

Теперь более-менее общее описание алгоритма:

Сразу сокращаем исходное выражение, пример: $[7]_{5} = [2]_{5}$

Добиваемся чётной степени путём выноса множителя и добавления его в список (при добавлении в список на любителя, можно копить элементы и потом их попарно умножать, либо оптимизировать и при добавлении элемента смотреть, если там уже один есть, то мы просто перемножаем добавляемый с уже имеющимся и записываем остаток при делении на модуль — таким образом «список» никогда не вырастет больше одного элемента и по-сути не станет «списком»)

Повторяем предыдущий пункт нужное кол-во раз

Перемножаем между собой элементы списка (эффективно, тоесть используя свойства применяемые выше), и оставшейся элемент в списке перемножаем с полученным элементом операцией «понижения степени» и получаем результат (не забываем что он должен быть тоже поделён на модуль и ответ — остаток — хотя это не обязательно — так как это эквивалентные числа)

Вот и всё, пора показать пример на python (кому было непонятно описание выше — поможет код):

def Zpow(a, p, m): """ Функция возведения в степень по модулю принимает 3 аргумента a - сам математический аргумент, возводимое число p - степень m - модуль """ result = 1 while p > 2: # когда степень сократится до квадрата и меньше - завершаем if p % 2 == 0: # если степень кратна 2 a = (a ** 2) % m p = p // 2 # целочисленное деление (на всякий) else: result = (result * a) % m p = p - 1 a = (a ** p) % m result = (result * a) % m return result

Можете поиграть с этой функцией — она очень быстро считает, и так как в Питоне по умолчанию все числа Большие, то попробуйте вбивать самые большие числа в аргументы этой функции, какие взбредут вам в голову!!!
В Криптоусиках, также реализована эта функция — и я всячески старался повесить сервак — не получилось.

Зная сколько студентов на лабах по-программированию сломали голову с этой процедурой возведения в степень по-модулю, я думаю этот материал будет полезен.

§ 4. Приближенное вычисление иррациональных чисел

Теперь
такой вопрос: как возвести число в
иррациональную степень? Например, нам
хочется узнать, что такое 10^²
.
Ответ
в принципе очень прост. Возьмем вместо

2
его
приближение в виде конечной десятичной
дроби — это рациональное число. Возводить
в рациональную степень мы умеем; дело
сводится к возведению в целую степень
и извлечению корня. Мы получим приближенное
значение числа
10^²
. Можно взять десятичную дробь подлиннее
(это снова рациональное число). Тогда
придется извлечь корень большей степени;
ведь знаменатель рациональной дроби
увеличится, но зато мы получим более
точное приближение. Конечно, если взять
приближенное значение 2
в
виде очень длинной дроби, то возведение
в степень будет делом очень трудным.
Как справиться с этой задачей?

Вычисление
квадратных корней, кубичных корней и
других корней невысокой степени —
вполне доступный нам арифметический
процесс; вычисляя, мы последовательно,
один за другим, пишем знаки десятичной
дроби. Но для того, чтобы возвести в
иррациональную степень или взять
логарифм (решить обратную задачу), нужен
такой труд, что применить прежнюю
процедуру уже не просто. На помощь
приходят таблицы. Их называют таблицами
логарифмов или таблицами степеней,
смотря по тому, для чего они предназначены.
Они экономят время: чтобы возвести число
в иррациональную степень, мы не вычисляем,
а только перелистываем страницы.

Хотя вычисление
собранных в таблицы значений — процедура
чисто техническая, а все же дело это
интересное и имеет большую историю.
Поэтому посмотрим, как это делается. Мы

вычислим
не только x=10
^V2
, но решим и другую задачу: 10^x=2,
или x=log₁₀2.
При
решении этих задач мы не откроем новых
чисел; это просто вычислительные задачи.
Решением будут иррациональные числа,
бесконечные десятичные дроби, а их
как-то неудобно объявлять новым видом
чисел.

Подумаем,
как решить наши уравнения. Общая идея
очень проста. Если вычислить 10¹
и 10¹^/¹⁰,
и 10¹^/100,
и 10¹^/¹⁰⁰⁰,
и т. д., а затем перемножить результаты,
то мы получим 10¹^,⁴¹⁴^…,
или
10
^²
. Поступая так, мы решим любую задачу
такого рода. Однако вместо 10¹^/¹⁰
и т. д. мы будем вычислять 10¹^/²,
10¹^/⁴
и т. д. Прежде чем начинать вычисления,
объясним еще, почему мы обращаемся
к числу 10 чаще, чем к другим числам. Мы
знаем, что значение таблиц логарифмов
выходит далеко за рамки математической
задачи вычисления корней, потому что

log_b(ac)=
log_ba+log_bc.

(22.3)

Это
хорошо известно всем, кто пользовался
таблицей логарифмов, чтобы перемножить
числа. По какому же основанию b
брать
логарифмы? Это безразлично; ведь в основу
таких вычислений положен только
принцип, общее свойство логарифмической
функции. Вычислив логарифмы один раз
по какому-нибудь произвольному
основанию, можно перейти к логарифмам
по другому основанию при помощи умножения.
Если умножить уравнение (22.3) на 61, то оно
останется верным, поэтому если перемножить
все числа в таблице логарифмов по
основанию b
на
61, то можно будет пользоваться и такой
таблицей. Предположим, что нам известны
логарифмы всех чисел по основанию b.
Иначе
говоря, можно решить уравнение b^а=с
для
любого с; для этого существует таблица.
Задача состоит в том, как найти логарифм
этого же числа с
по
другому основанию, например х.
Нам
нужно решить уравнение х^а‘=с.
Это
легко сделать, потому что

х
всегда
можно представить так: x=b^t.
Найти
t,
зная
х
и
b,
просто:
t=log_bx.
Подставим
теперь х=b^t
в
уравнение x^a’
=с;
оно
перейдет в такое уравнение: (b^t)^а‘=b^ta’=с.
Иными словами, произведение ta’
есть
логарифм с
по
основанию b.
Значит,
a’=a/t.
Таким
образом, логарифмы по основанию х
равны
произведениям логарифмов по основанию
b
на
постоянное число 1/t.
Следовательно,
все таблицы логарифмов эквивалентны с
точностью до умножения на число 1/log_bx.
Это
позволяет нам выбрать для составления
таблиц любое основание, но мы решили,
что удобнее всего взять за основание
число 10. (Может возникнуть вопрос: не
существует ли все-таки какого-нибудь
естественного основания, при котором
все выглядит как-то проще? Мы попытаемся
ответить на этот вопрос позднее. Пока
все логарифмы будут вычисляться по
основанию 10.
)

Теперь
посмотрим, как составляют таблицу
логарифмов. Работа начинается с
последовательных извлечений квадратного
корня из 10. Результат можно увидеть в
табл. 22.1. Показатели степеней записаны
в ее первом столбце, а числа 10^S—
в третьем. Ясно, что 10¹=10.
Возвести
10 в половинную степень легко — это
квадратный корень из 10, а как извлекать
квадратный корень из любого числа, знает
каждый.
Итак, мы нашли первый квадратный корень;
он равен 3,16228. Что это дает? Кое-что дает.

Таблица
22.1 • последовательные
извлечения

КВАДРАТНОГО КОРНЯ
ИЗ 10

Мы уже
можем сказать, чему равно 10^0,5,
и знаем по крайней мере один
логарифм.
Логарифм числа 3,16228
очень
близок к 0,50000. Однако нужно еще приложить
небольшие усилия: нам нужна более
подробная таблица. Извлечем еще один
квадратный корень и найдем 10^1/4,что
равно 1,77828. Теперь мы знаем еще один
логарифм: 1,250— это логарифм числа 17,78;
кроме того, мы можем сказать, чему равно
10^0,75:
ведь это 10⁽⁰^,⁵⁺⁰^,²⁵⁾,
т. е. произведение второго и третьего
чисел из третьего столбца табл. 22.1. Если
сделать первый столбец таблицы достаточно
длинным, то таблица будет содержать
почти все числа; перемножая числа из
третьего столбца, мы получаем 10 почти
в любой степени. Такова основная идея
таблиц. В нашей таблице содержится
десять последовательных корней из 10;
основной труд по составлению таблицы
вложен в вычисления этих корней.

Почему
же мы не продолжаем повышать точность
таблиц дальше? Потому что мы кое-что уже
подметили. Возведя 10 в очень малую
степень, мы получаем единицу с малой
добавкой. Это, конечно, происходит
потому, что если возвести, например,
10¹^/¹⁰⁰⁰
в 1000-ю степень, то мы снова получим 10;
ясно, что `0^1/¹⁰⁰⁰
не может быть большим числом: оно очень
близко к единице. Более того, малые
добавки к единице ведут себя так, будто
их каждый раз делят на 2; поглядите-ка
на таблицу повнимательнее: 1815 переходит
в 903, потом в 450, 225 и т. д. Таким образом,
если вычислить еще один, одиннадцатый,
квадратный корень, он с большой точностью
будет равен 1,00112, и этот результат мы
угадали
еще
до вычисления. Можно ли сказать, какова
будет добавка к единице, если возвести
10 в степень
/1024,
когда 
стремится к нулю? Можно. Добавка будет
приблизительно равна 0,0022511.
Конечно, не в точности 0,0022511 ;
чтобы вычислить эту добавку поточнее,
делают такой трюк: вычитают из 10^S
единицу
и делят разность на показатель степени
s.
Отклонения
полученного таким образом частного
от его точного значения одинаковы для
любой степени s.
Видно,
что эти отношения (см. четвертый столбец
табл. 22.1) примерно равны. Сначала они
все-таки сильно отличаются друг от
друга, но потом все ближе подходят друг
к другу, явно стремясь к какому-то числу.
Что это за число? Проследим, как меняются
числа четвертого столбца, если опускаться
вниз по столбцу. Сначала разность двух
соседних чисел равна 0,0211, потом 0,0104,
потом 0,0053 и, наконец, 0,0026. Разность каждый
раз убывает наполовину. Сделав еще один
шаг, мы доведем ее до 0,0013, потом до 0,0007,
0,0003, 0,0002 и, наконец, примерно до 0,0001; надо
последовательно делить 26 на 2. Таким
образом, мы спустимся еще на 26 единиц
и найдем для предела

2.3025. (Позднее мы
увидим, что правильнее было бы взять

2.3026. но давайте
возьмем то, что у нас получилось.)
Пользуясь этой таблицей, можно возвести
10 в любую степень, если ее показатель
каким угодно способом выражается через
1/1024. Теперь легко составить таблицу
логарифмов, потому что все необходимое
для этого мы уже припасли. Процедура
этого изображена в табл. 22.2, а нужные
числа берутся из второго и третьего
столбцов табл. 22.1.

Таблица
22.2 •
ВЫЧИСЛЕНИЯ log₁₀2

Предположим,
что мы хотим знать логарифм 2. Это значит,
что мы хотим знать, в какую степень надо
возвести 10, чтобы получить 2. Может быть,
возвести 10 в степень ¹/₂?
Нет, получится слишком большое число.
Глядя на табл. 22.1, можно сказать, что
нужное нам число лежит между ¹/₄
и ¹/₂.
Поиск
его начнем с ¹/₄;
разделим
2 на 1,788…, получится 1,124…; при делении
мы отняли от логарифма двух 0,250000, и
теперь нас интересует логарифм 1,124….
Отыскав его, мы прибавим к
результату
¹/₄=256/1024.
Найдем
в табл. 22.1 число, которое бы при движении
по третьему столбцу сверху вниз стояло
сразу за 1,124… . Это 1,074607. Отношение
1,124… к 1,074607 равно 1,046598. В конце концов
мы представим 2 в виде произведения
чисел из табл. 22.1:

2=(1,77828)•(1,074607)•(1,036633)
• (1,0090350)•(1,000573).

Для
последнего множителя (1,000573) в нашей
таблице места не нашлось; чтобы найти
его логарифм, надо представить это число
в виде 10^/¹⁰²⁴1+2,3025/1024.
Отсюда легко найти, что =0,254.
Таким образом, наше произведение можно
представить в виде десятки, возведенной
в степень 1/1024 (256+32+16+4+0,254). Складывая и
деля, мы получаем нужный логарифм:
log₁₀2=0,30103;
этот результат верен до пятого десятичного
знака!

Мы
вычисляли логарифмы точно так же, как
это делал мистер Бриггс из Галифакса в
1620 г. Закончив работу, он сказал: «Я
вычислил последовательно 54 квадратных
корня из 10». На самом деле он вычислил
только 27 первых корней, а потом сделал
фокус с .
Вычислить 27 раз квадратный корень из
10, вообще-то говоря, немного сложнее,
чем 10 раз, как это сделали мы. Однако
мистер Бриггс сделал гораздо большее:
он вычислял корни с точностью до
шестнадцатого десятичного знака, а
когда опубликовал свои таблицы, то
оставил в них лишь 14 десятичных знаков,
чтобы округлить ошибки. Составить
таблицы логарифмов с точностью до
четырнадцатого десятичного знака
таким методом — дело очень трудное.
Зато целых 300 лет спустя составители
таблиц логарифмов занимались тем, что
уменьшали таблицы мистера Бриггса,
выкидывая из них каждый раз разное число
десятичных знаков. Только в последнее
время при помощи электронных вычислительных
машин оказалось возможным составить
таблицы логарифмов независимо от
мистера Бриггса. При этом использовался
более эффективный метод вычислений,
основанный на разложении логарифма в
ряд.

Составляя
таблицы, мы натолкнулись на интересный
факт: если показатель степени 
очень мал, то очень легко вычислить 10^;
это просто 1+2,3025е. Это значит, что
10ⁿ/²^,³⁰²⁵
=1+n
для
очень малых n.
Кроме
того, мы говорили с самого начала, что
вычисляем логарифмы по основанию 10
только потому, что у нас на руках 10
пальцев и по десяткам нам считать
удобнее. Логарифмы по любому другому
основанию получаются из логарифмов
по основанию 10 простым умножением.
Теперь настало время выяснить, не
существует ли математически выделенного
основания логарифмов, выделенного по
причинам, не имеющим ничего общего с
числом пальцев на руке. В этой естественной
шкале
формулы
с логарифмами должны выглядеть
проще.
Составим новую таблицу логарифмов,
умножив все логарифмы по основанию 10
на 2,3025…. Это соответствует переходу
к новому основанию — натуральному,
или
основанию е.
Заметим,
что log_
(l+n)n
или
еⁿ1+n,
когда n0.

Легко
найти само число е;
оно
равно 10¹/²^,³⁰²⁵
или 10⁰^,⁴³⁴²⁹⁴^…Это
10 в иррациональной степени. Для вычисления
е
можно
воспользоваться таблицей корней из 10.
Представим 0,434294… сначала в виде
444,73/1024, а числитель этой дроби в виде
суммы 444,73=256+128+32+16+2+0,73. Число е
поэтому
равно произведению чисел

(1,77828)•(1,33352)•(1,074607)•(1,036633)•(1,018152)X(1,009035)(1,001643)
=2,7184.

(Числа
0,73 нет в нашей таблице, но соответствующий
ему результат можно представить в
виде 1+2,3025
и вычислить, чему равна .)
Перемножив все 7 сомножителей, мы получим
2,7184 (на самом деле должно быть 2,7183, но и
этот результат хорош). Используя такие
таблицы, можно возводить число в
иррациональную степень и вычислять
логарифмы иррациональных чисел. Вот
как надо обращаться с иррациональностями.

экспонентов, правила, которые дадут вам большую власть над числами

08.05.2018
|
0

Эпизод №7 курса «Основы математики» Джона Робина

Вы готовы углубиться в следующую тему нашего курса «Основы математики»? Сегодня мы познакомимся с удивительным миром экспонентов.

В уроке 3 я показал вам, как использовать показатели степени, когда мы учились записывать произведение простых чисел в любом составном числе. Например, я упомянул, что 288 — это 2x2x2x2x2x3x3, но более компактным способом записи было бы 2 ⁵ (3 ² ). 1024 — это 2x2x2x2x2x2x2x2x2x2. 2 умножается на десять. Таким образом, в экспоненциальной записи мы бы просто написали:

1024 = 2 ¹⁰

Гораздо проще!

В этом показателе число 2 называется основанием, а число 10 — показателем степени. Думайте о базе как о числе, которое многократно умножается. Это ваша отправная точка, она же домашняя база.

Теперь, точно так же, как у нас были некоторые правила с двумя квадратными корнями, у нас есть правила о том, что происходит, когда два показателя степени сходятся вместе.

Давайте поработаем с числом 2 в качестве нашего примера (но учтите, что вы можете использовать любое число).

1. Если перемножить два одинаковых основания, объединить их и прибавить их степени:

Это то же самое, что сказать:

2 ³ x 2 ⁸ = 2 3 14 3 14 3 11 3 это с точки зрения того, откуда пришли экспоненты. 2 ³ это 2x2x2. 2 ⁸ равно 2x2x2x2x2x2x2x2. Сколько всего двоек (оснований) есть? 3 + 8 = 11,

2. Если два одинаковых основания делятся друг на друга, сложите их и вычтите их степени:

Это то же самое, что сказать:

(2 ⁸ ) / (2 ³ ) = 2 ⁵

Подумайте об этом с точки зрения происхождения показателей. 2 ⁸ равно 2x2x2x2x2x2x2x2. 2 ³ это 2x2x2.

Как это выглядит дробью?

(2x2x2x2x2x2x2x2) / (2x2x2)

Мы можем вычеркнуть 2 в числителе вместо каждых 2 в знаменателе, оставив 2x2x2x2x2, т. е. 2 ⁵ . Это то же самое, что вычесть количество двоек в знаменателе (3) из количества двоек в числителе (8).

3. Если основание степени само по себе является основанием другого числа степени, умножьте степени вместе:

Это немного сложнее. Это выглядит так:

(2 ³ ) ⁸ = 2 ²⁴

Здесь две базы. Первый внутри равен 2. Он возведен в степень 3. Второй равен (2 ³ ). Все это действует как одно основание, возведенное в степень 8.

Чтобы понять, что здесь происходит, давайте снова посмотрим на это с точки зрения того, что делают показатели степени:

2 ³ = 2x2x2.

Итак, у нас есть:

(2x2x2) ⁸

Показатель степени 8 говорит нам умножить (2x2x2) сам на себя восемь раз. Это выглядит так:

(2x2x2)x(2x2x2)x(2x2x2)x(2x2x2)x(2x2x2)x(2x2x2)x(2x2x2)x(2x2x2)

Глаза болят? Смотрите на него ровно столько, чтобы убедиться, что (2 ³ ) ⁸ равно 2 ²⁴, потому что 2 ³ умножается само на себя восемь раз, что равносильно умножению 2 на себя 24 (3×8) раза.

4. Отрицательная экспонента переворачивает дробь, затем становится положительной:

Проще говоря:

2 ^-1 = 1/2

(1/2) ^-1 = 2 0 3/59) ^-1 = (59/3)

Если показатель степени больше 1, вы просто применяете правила с первого по третий выше к тому, что осталось:

(2 ³ ) / (2 ⁸ ) = 2 ^-3 = (1/2) ³ = (1/8)

знаменатель — корень:

До сих пор мы много работали с квадратными корнями: √7, √2, √3. В качестве показателя степени квадратный корень имеет показатель степени 1/2:

√7 = (7) ^1/2

Подумайте о том, что мы уже узнали о показателях степени. Показатель степени говорит нам, сколько раз нужно умножить число само на себя. В случае квадратного корня мы умножаем его на себя в 1/2 раза. Выполнение этого дважды вернет нам номер.

Используя эту идею, мы можем видеть, например, что кубический корень, записанный как ³ √7, будет тремя равными числами, которые вместе дают 7. В записи экспоненты это будет (7) ^1/3, и мы можем представить это как 7, умноженное само на себя в 1/3 раза.

Мы можем расширить это до любого корня, ⁿ √7 (в качестве примера я использую 7, но вы можете поместить туда любое основание). Они называются n-ми корнями.

Если у вас показатель степени дроби с числителем больше 1, вы просто применяете правила с первого по четвертое, указанные выше:

16 ^3/4 = ( ⁴ √16) ³ = (2) ³ = 8

И вот посмотрите, что мы можем сделать с показателями степени. Оставайтесь с нами на завтрашнем уроке, где мы будем изучать их близких родственников: логарифмы.

Поделись с друзьями

Обретение Высшей Силы – 5 практических способов повысить духовное осознание

«Доверься Богу. Чистый дом. Помочь другим.» Мы все слышали это раньше.

Звучит достаточно просто, но так ли это на самом деле? Наиболее распространенная форма опасений в организациях по восстановлению, особенно в программах, основанных на двенадцати шагах, заключается в концепции поиска высшей силы. Я слышал, как люди бесчисленное количество раз говорили, что «они не понимают всей сути Бога». Эта неуверенность не бесполезна, и, к сожалению, нежелание найти высшую силу мешает многим наркоманам найти выздоровление и равновесие.

В этой статье мы надеемся поделиться личным опытом относительно того, что значит найти высшую силу, и, что более важно, почему вера в силу, более могущественную, чем вы сами, имеет огромные преимущества в выздоровлении и в жизни.

Бог и двенадцать шагов

Очень немногие люди приходят в программу двенадцати шагов с ясным пониманием своих верований, и еще меньше людей живут в соответствии с духовными принципами. «Жить в» духовных принципах — это концепция, изложенная в Большой Книге Анонимных Алкоголиков . Самая большая ошибка, которую совершают люди, состоит в том, что они полагают, что высшая сила является предопределенной концепцией, которую они вынуждены принять. В Большой Книге ясно сказано, что человек должен «избрать Бога по своему собственному пониманию». Это очень сбивает с толку многих людей. Так что же это означает?

Нам нравится быть очень простыми и непредвзято относиться к вопросам Бога. Идеи будут отличаться от человека к человеку. Я расскажу о своем собственном опыте путешествия, которое я предпринял, чтобы найти высшую силу, и о том, как это помогло мне.

Высшая сила — это нечто большее, чем вы сами. Идея проста. Это то, к чему нужно принадлежать. Людям нужно чувствовать связь с чем-то. Человеческий инстинкт требует, чтобы мы чувствовали себя «частью» и чувствовали себя принадлежащими. Для меня высшая сила была чем-то таким же простым, как энергия.

Как и многие другие молодые люди, выздоравливающие, я был озадачен тем, как Бог в моем понимании может помочь мне. Я спросил: «Какое отношение ко всему этому имеет Бог?»

Многие наркоманы проводят свою жизнь на пути своеволия. Своеволие и контроль — это иллюзия; оно существует только в нашем собственном восприятии реальности. Обретение высшей силы — это способ отказаться от контроля и, следовательно, отказаться от бремени будущего. Единственное, что каждый из нас может контролировать, это собственные действия . Вот и все. Все остальное находится и всегда будет полностью вне нашего контроля. «Отдать это Богу» — это просто средство для принятия. Чем ближе вы связаны со своей высшей силой, тем легче передать вещи.

Наука и духовность

Когда я впервые услышал об этой идее, я занял оборонительную позицию. Я провел так много лет, думая, что Бог был просто механизмом, созданным людьми, чтобы внести ясность в то, чего мы не понимаем. Меня не устраивала и до сих пор не устраивает мысль о том, что жизнь предопределена для нас Богом. Я аналитичен и люблю эмпирические данные.

В начале моего выздоровления я просто принимал все за чистую монету. Я действовал согласно предложениям, данным мне другими людьми. Я слышал, что если бы я делал все это, то оставался бы трезвым, а это то, чего я хотел. Однако я не мог отрицать, что очень немногое из этого имело для меня смысл. Но я продолжал искать.

Вот что случилось со мной. Я говорю это не для того, чтобы навязать вам свои убеждения. Я просто указываю, что если я могу найти высшую силу, то это возможно и для любого другого, у кого могут быть сомнения.

Я всегда считал, что все во Вселенной имеет энергию. Более того, все ЯВЛЯЕТСЯ энергией. Это научно доказано. Все связано. Я изучал эту идею. Мне стало ясно, что наука и духовность на самом деле не так уж сильно отличаются.

Все во Вселенной связано; растения, небо, звезды и даже гравитация. Все это взаимодействует в совершенной гармонии, чтобы создать это прекрасное существование и взаимосвязь энергии. Я понял, что у меня уже есть высшая сила. Меня не нужно было убеждать, потому что это было основано на фактах. Я обнаружил, что просто быть живым означало, что я был связан со всеми вокруг меня и со всем, что когда-либо будет существовать. Это было такое откровение. Я нашел, во что верить. Тогда я еще не понимал, зачем мне это нужно.

Как мне может помочь Высшая Сила??

Жизнь по собственной воле приносит большое давление. Когда мы пытаемся контролировать исход вещей, мы обнаруживаем, что у нас мало успеха. Что бы ни случилось, происходит без нашего согласия. Понимание того, что за всем стоит управляющая сила, снимает бремя контроля. Что бы ни случилось, это просто произойдет. Правда в том, что ни вы, ни я, ни кто-либо другой мало что могут сделать, чтобы контролировать исход жизни.

Отказ от контроля над результатами освободит ваш разум и дух. Не позволяйте дилемме Высшей Силы помешать вам жить своей жизнью.

Аналогия, которую я нахожу полезной, — плыть по течению реки. Река собирается течь, однако она решает течь. Река сильнее меня. Я не могу контролировать реку. Что я могу контролировать, так это мои действия. Если я застрял в реке, я могу бороться с течением. Это утомит меня, и я никуда не денусь. Я буду тратить энергию. Мой другой вариант — позволить реке нести меня своим курсом. Таким образом, я могу экономить свою энергию и жить с результатами того, где моя высшая сила решает, что я должен быть. Трудно не бороться с течением. Трудно смиренно признать, что я ничего не могу сделать. Уверяю вас, позволить течению жизни унести вас гораздо проще и гораздо приятнее.

Высшая сила даст вам то, к чему вы будете принадлежать. Принадлежность к чему-то более сильному, чем вы сами, дает вам силу, потому что вы больше не одиноки. Вы будете подключены к бесконечному количеству энергии. Нам нужно только отпустить контроль и прислушаться к тому, куда нас направляет наша высшая сила. Мы все хотим чувствовать связь.

Как найти высшую силу?

Я понимаю, что то, что я сказал, может не иметь смысла для всех. Что наиболее важно, так это то, что это послание доходит до тех, кто все еще не понимает Бога. Все это звучит хорошо и величественно, но как кто-то может поверить?

Вот несколько простых советов, которые помогут вам найти то, что вы ищете.

1 – Будьте открытыми

Слушайте все, что говорят люди. Вы не обязаны соглашаться со всеми. Вы имеете абсолютно право не соглашаться с чьими-либо взглядами. Тем не менее, слушайте с открытым сознанием. Усвойте информацию, а затем примите решение, работает она на вас или нет. Вы обнаружите, что у вас больше общего с другими людьми, чем вы думаете.

2 — Медитация

Молчать. Слушать. В жизни, и особенно в нашем обществе, так трудно успокоить свой ум. Очень трудно найти покой, когда вокруг нас постоянно происходит столько шума. Посвятите некоторое время тому, чтобы побыть наедине с собой; ни музыки, ни мобильного телефона, ни телевизора. Сядьте спокойно и тренируйтесь быть в настоящем моменте. Делайте это последовательно, и вы достигнете новых глубин самопознания.

3 – Молитесь

Лично мне кажется, что когда я молюсь, меня никто не слушает. Я не уверен, что есть всезнающее божество, слушающее то, что я хочу сказать. Важно то, что когда вы молитесь, вы взаимодействуете со своей высшей силой. Вы формируете отношения с управляющими силами Вселенной. Я не могу объяснить, как и почему, но я обещаю вам, что Вселенная возразит.

4 -Помогайте людям

Когда вы служите другим, вы выходите за пределы себя. Когда мы помогаем другим людям, все наши собственные страхи и неуверенность исчезают, потому что мы сосредоточены на чем-то вне нас самих. Служение другим — прямая линия к пониманию высшей силы. Когда вы чувствуете результат доброго дела, это само по себе награда, и вы, вероятно, почувствуете себя частью чего-то гораздо большего.

5 – Продолжайте искать

Вы должны оставаться открытыми для новых идей и открытий. Никто никогда не сможет полностью понять Бога. Человеческое состояние не дает абсолютной ясности в этом.

Источник

Найти наибольшую степень числа 2, на какой делятся число (а,в).
а=7
в=7

@алексей911113: если речь о числе 7, то оно нечётно, поэтому делится на 2 в нулевой степени, то есть на $%2^0=1$%. На $%2^1$% оно уже не делится.

(15 Май ’15 23:53)
falcao

@алексей911113: если я правильно понял условие, то здесь больше ничего нет. Наверное, это не самостоятельная задача, а часть решения чего-то. Для примера: возьмём числа 10, 24, 40, 100, 101. Тогда для них максимальные степени числа 2, на которые они делятся, равны $%2^1$%, $%2^3$%, $%2^3$%, $%2^2$%, $%2^0$% соответственно. Просто надо посмотреть, сколько раз число можно последовательно делить на 2, пока все числа остаются целыми, вот и всё.

Уточнил задания

Найти наибольшую степень числа 2 на какой делятся число (а,в)! факториал

@алексей911113: в этом случае речь идёт о числе $%7!=5040$%. Можно или посмотреть, сколько раз это число делится на 2 (в понятном смысле), или проследить по отдельности чётные сомножители 2, 4, 6. Тогда будет ясно, что имеет место делимость на $%2cdot2^2cdot2=2^4$%, а на $%2^5$% число уже не делится.

(16 Май ’15 13:02)
falcao

Источник