Расскажем простыми словами, что это такое NPV (Net Present Value). Покажем формулы и методы расчета чистой приведенной стоимости всех денежных потоков инвестиционного проекта с помощью ставки дисконтирования.
Откройте счет
в БКС Мир Инвестиций
Зачем нужно считать NPV (Net Present Value)
NPV (чистая приведенная стоимость) — это метод, который позволяет вычислить ожидаемую доходность с учетом изменения ценности денежных потоков (дисконтирования).
Финансовый показатель нужен для того, чтобы сопоставить будущую прибыль с текущими вложениями. Таким образом можно оценить, стоит ли инвестировать в тот или иной проект, окупятся ли вложенные средства и насколько вероятен риск убытков. Также с помощью NPV сравнивают инвестиционные проекты, чтобы выявить из них более привлекательный по критерию прибыльности.
Преимущества и недостатки подсчета чистой приведенной стоимости
Главное преимущество NPV состоит в том, что с помощью показателя можно произвести оценку инвестиционной привлекательности проекта. При расчетах допустимо учитывать дополнительные составляющие: срок жизни проекта и распределение денежных потоков во времени. Также одним из плюсов NPV является возможность складывать показатели различных проектов.
Основные недостатки NPV — это сложность расчетов и относительно низкая достоверность. Если говорить об ожидаемой прибыли, которую планирует получить инвестор, то показатель может отразить ее некорректно. Все дело в ряде факторов, влияющих на точность расчетов: например, ставка дисконтирования имеет свойство меняться, как и показатель инфляции. Эти риски можно принимать во внимание при проведении расчетов, но вместе с ними возрастает и сложность вычислений.
На практике организации чаще используют другой показатель для оценки проектов — IRR (внутренняя норма доходности). Он позволяет определить максимальную ставку кредита, которая позволительна для того, чтобы инвестиционный проект не был убыточным.
Формула расчета
Рассмотрим формулу, по которой можно рассчитать NPV:
где:
n — временной отрезок, за который производится расчет;
Pk — денежный поток за выбранный интервал времени;
i — ставка дисконтирования;
IC — капитал, вложенный на этапе первоначальных инвестиций.
Денежные потоки инвестиционного проекта
Денежные потоки — это разница между доходами и расходами компании или проекта.
Одним из самых сложных пунктов при расчете NPV является учет всей массы денежных потоков. Для этого необходимо соотнести размер первоначально вложенного капитала, а также ожидаемую прибыль и планируемые расходы в будущем.
Сложность состоит в том, что при подсчете денежных потоков следует учесть множество нюансов: экономическую ситуацию, наличие спроса, если ваш инвестиционный проект связан с производством, конкурентную составляющую и так далее.
Также необходимо произвести расчеты, которые связаны с потенциальными операционными расходами. В свою очередь, они напрямую зависят от ряда факторов: размера заработной платы сотрудников, занятых в проекте, стоимости сырьевого обеспечения, динамики курсов валют и других показателей.
Ставка дисконтирования простыми словами
Ставка дисконтирования — это инструмент для прогнозирования, который позволяет оценить доходность будущих инвестиций. При этом полученный результат выражается в текущей стоимостной величине.
Если говорить простыми словами, то ставка дисконтирования позволяет рассчитать стоимость будущего дохода по меркам настоящего времени. Это эталонная величина, которая используется для приведения будущих денежных потоков к одному знаменателю. Например, чтобы оценить, стоит ли инвестировать финансовые средства в тот или иной инструмент и какой доход он принесет в будущем по отношению к настоящему моменту.
Как рассчитать NPV
Рассмотрим, как рассчитать чистую приведенную стоимость, на примере. Допустим, капитал, инвестированный в качестве стартовых вложений, составит 500 тысяч рублей. Временной интервал, за который будут производиться вычисления, — 1 год. Также необходимо определить ставку дисконтирования: в нашем примере она будет равна 10% (показатель рассчитывается как коэффициент, поэтому его значение мы определим как 0,1). Дополнительно следует предположить, какой размер денежных поступлений планируется: например: 300 тысяч рублей.
300 000 ₽ / (1+0,1) – 500 000 ₽ = –227 273 ₽
В итоге мы получили число, которые выражает чистую прибыль за годовой период. Так как ниже нуля, то данный инвестиционный проект можно назвать убыточным на выбранном отрезке времени. Но если мы увеличим количество таких периодов, то получит другое значение.
Рассчитаем NPV за 3 года, учитывая, что в каждом из них ставка дисконтирования будет уменьшаться.
300 000 ₽ / (1+0,1) + 300 000 ₽ / (1+0,1)² + 300 000 ₽ / (1+0,1)³ + 300 000 ₽ / (1+0,1)⁴ – 500 000 ₽ = 518 952 ₽
Сумма, полученная в результаты вычислений, положительная, а это означает, что по прошествии трех лет данный инвестиционный проект окупится и будет приносить прибыль.
Пример расчета в MS Excel
Для быстроты и удобства можно также применить инструмент таблицы в MS Excel. Этот метод позволит не производить вычисления самостоятельно и поможет избежать возможных ошибок, возможных при расчетах вручную. Для начала заполните все поля таблицы необходимыми данными.
Затем используйте ЧПС — специальную функцию для вычисления NPV. Для этого в ячейку B10 необходимо добавить формулу, приведенную на картинке ниже.
Таблица произведет расчеты самостоятельно, и вы увидите результат в ячейке B10.
Полученная сумма в нашем примере отрицательное. Это значит, что инвестиционный проект невыгоден и не окупиться за 3 года.
Популярные ошибки при расчете
Игнорирование сопутствующих расходов
Допустим, инвестор планирует приобрести оборудование для производства автомобильных деталей и продавать их по определенной стоимости. В этом случае необходимо учесть расходы на износ и амортизацию оборудования, а это — дополнительные деньги в качестве трат. Если не учесть их при вычислении, NPV будет ошибочным;
Завышенные ожидания от проекта
При расчете NPV следует опираться на реалистичные прогнозы, ведь доходность зависит от множества факторов. Недальновидно ожидать, что приток пользователей вашего проекта будет динамично расти, а вместе с ним и размер прибыли. Ведь у каждого бизнеса есть периоды простоя: например, из-за фактора сезонности;
Некорректное значение ставки дисконтирования
Для расчета показателя используется ряд методов, каждый из которых учитывает различные исходные данные. Спустя некоторое количество времени значения могут меняться (например, уровень инфляции), соответственно, рассчитанная ранее чистая приведенная стоимость станет неактуальной.
Выводы для инвестора
Метод чистой приведенной стоимости используется, чтобы рассчитать ожидаемую доходность инвестиционного проекта и сроки его окупаемости;
Для вычисления NPV понадобится учесть ряд показателей: стартовый капитал, вложенный в проект в качестве персональных инвестиций, ставку. дисконтирования, временной отрезок и денежные потоки за выбранный период;
Для более корректного результата необходимо включить в расчете все предполагаемые риски, с которыми можно столкнуться в ходе проекта.
Инвестируйте из любой точки мира, покупайте и продавайте валюту по выгодному курсу, пользуйтесь умными подсказками и качественной аналитикой.
Приложение БКС Мир инвестиций
Отсканируйте QR-код и скачайте приложение
Прогноз цены: как применять технический и фундаментальный анализ рынка
Как составить личный финансовый план. Пошаговая инструкция
Формула для расчета FV
Формула будущей стоимости (FV) — это финансовая терминология, используемая для расчета стоимости денежного потока на футуристическую дату по сравнению с исходным чеком. Целью этого уравнения FV является определение будущей стоимости предполагаемых инвестиций и того, приносят ли доходы достаточную прибыль с учетом временной стоимости денег. Фактор временной стоимости денег Принцип временной стоимости денег (TVM) гласит, что деньги, полученные в настоящее имеет большую ценность, чем деньги, полученные в будущем, потому что деньги, полученные сейчас, могут быть инвестированы и использованы для создания денежных потоков для предприятия в будущем в виде процентов или за счет будущей прироста стоимости инвестиций и реинвестирования. Подробнее.
Формула будущей стоимости (FV):
FV=C0 * (1+r)n
Посредством чего,
- C0 = Денежный поток в начальный момент (текущая стоимость)
- г = норма прибыли
- n = количество периодов
Оглавление
- Формула для расчета FV
- Пример
- Использование и актуальность
- Калькулятор будущей стоимости
- Видео о формуле будущей ценности
- Рекомендуемые статьи
Пример
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}
Вы можете скачать этот шаблон Excel Future Value (FV) здесь – Будущая стоимость (FV) Шаблон Excel
Если у миссис Смит есть 9000 долларов на банковском счете, и она получает годовой процент в размере 4,5%. С помощью формулы будущего ее счет через 15 лет будет:
- БФ = 9000 * (1 + 0,045) ^ 15
- ФВ = 9000 * (1,045) ^ 15
- ФВ = 9000 * 1,935
- БС = 17 417,54 долл. США
Мы можем рассмотреть другой пример для лучшего понимания:
У миссис Смит есть еще один счет, на котором есть 20 000 долларов США с годовой ставкой 11%, начисляемой ежеквартально. Начисление процентов на ежеквартальной основе. Формула начисления сложных процентов отражает общую сумму процентов, которые инвестор может заработать на инвестициях или финансовых продуктах, если проценты выплачиваются ежеквартально и реинвестируются в схема. Он учитывает основную сумму, ежеквартальную начисленную процентную ставку и количество периодов для расчета. Подробнее. С 1 января 2017 года условия договора продлены, а начисление сложных процентов происходит два раза в месяц. Миссис Смит хочет рассчитать общую стоимость счета на 31 декабря 2017 г.?
Для начала нам необходимо получить начальное сальдо на 1 января 2017 года:
- PV (16 января — 16 декабря) = 20 000 долларов США.
- Период начисления (n) = 4
- Годовая процентная ставка (r) = 11%, которая конвертируется в квартальную процентную ставку 2,75% [11% / 4]
- БС = 20 000 * (1 + 0,0275) ^ 4
- БС = 20 000 * (1,0275) ^ 4
- FV = 22 292,43 долл. США (начальный баланс на 1 января 2017 г.)
Таким образом, теперь для расчета будущей стоимости по состоянию на 31 декабря 2017 года текущая стоимость составляет 22 292,43 доллара США.
Период начисления сложных процентов (n) теперь равен 2*12 = 24, поскольку сложные процентыСложные процентыСложные проценты — это проценты, начисляемые на сумму основной суммы и общих процентов, начисленных на нее до сих пор. Это играет решающую роль в получении более высоких вознаграждений от инвестиций. Теперь два раза в месяц.
Годовая процентная ставка (r) = 11%, которая преобразует месячную процентную ставку = 11%/12 = 0,0092. [this will further be split twice a month thus, 0.92/2 = 0.0046%]
- Таким образом, FV = PV (1 + r) ^ n
- БС = 22 292,43 * (1 + 0,0046) ^ 24
- БС = 22 292,43 * (1,00046) ^ 24
- БС = 22 292,43 * 1,116
- БС = 24 888 долларов США [Value of the account as on December 31, 2017]
Использование и актуальность
- Основное преимущество FV заключается в том, чтобы определить, принесет ли инвестиционная возможность достаточную доходность в будущем.
- Концепция применима к личным и корпоративным решениям.
- Цель состоит в том, чтобы иметь представление о том, как экономические факторыEconomic FactorsEconomic являются внешними факторами окружающей среды, которые влияют на эффективность бизнеса, такие как процентные ставки, инфляция, безработица и экономический рост, среди прочего.Подробнее, могут повлиять на доходы, такие как Инфляция, уровень жизни, операционные расходы/повторяющиеся расходы (требуется отдельный анализ).
- Он показывает поток платежей, которые, как ожидается, будут получены в течение определенного периода времени, например, 10-летняя инвестиция может показать, какую прибыль можно получать каждый год.
- В определенных обстоятельствах формула также используется в качестве входных данных для других формул. Например, аннуитет в виде повторяющихся депозитов на интересующем счете будет FV каждого депозита.
Калькулятор будущей стоимости
Вы можете использовать следующий Калькулятор будущей стоимости
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } Формула C0rnFuture Value =
Формула будущей стоимости = C0 X (1 + r)n = 0 * (1 + 0)0 = 0
Видео о формуле будущей ценности
Рекомендуемые статьи
Это было руководство по Формуле Будущей Ценности. Здесь мы узнаем, как рассчитать будущую стоимость (FV), используя его формулу, а также практические примеры, калькулятор и загружаемый шаблон Excel. Вы также можете ознакомиться с приведенными ниже статьями, чтобы узнать больше о корпоративных финансах:
- Рассчитать PV
- Формула значения в ExcelФормула значения В ExcelВ Excel функция значения возвращает значение текста, представляющего число. Итак, если у нас есть текст со значением $5, мы можем использовать формулу значения, чтобы получить в результате 5, поэтому эта функция дает нам числовое значение, представленное текстом.Подробнее
- NPV против XNPV
What Is Future Value (FV)?
Future value (FV) is the value of a current asset at a future date based on an assumed rate of growth. The future value is important to investors and financial planners, as they use it to estimate how much an investment made today will be worth in the future.
Knowing the future value enables investors to make sound investment decisions based on their anticipated needs. However, external economic factors, such as inflation, can adversely affect the future value of the asset by eroding its value.
Future value can be contrasted with present value (PV).
Key Takeaways
- Future value (FV) is the value of a current asset at some point in the future based on an assumed growth rate.
- Investors are able to reasonably assume an investment’s profit using the FV calculation.
- Determining the FV of a market investment can be challenging because of market volatility and uncertainty about future investment conditions.
- There are two ways of calculating the FV of an asset: FV using simple interest, and FV using compound interest.
- Future value is opposed by present value (PV); the former calculates what something will be worth at a future date, while the other calculates what something at a future date is worth today.
Future Value
Understanding Future Value (FV)
The future value calculation allows investors to predict, with varying degrees of accuracy, the amount of profit that can be generated by different investments. The amount of growth generated by holding a given amount in cash will likely be different than if that same amount were invested in stocks; therefore, the future value equation is used to compare multiple options.
Determining the future value of an asset can become complicated, depending on the type of asset. Also, the future value calculation is based on the assumption of a stable growth rate. If money is placed in a savings account with a guaranteed interest rate, then the future value is easy to determine accurately. However, investments in the stock market or other securities with a more volatile rate of return can present greater difficulty.
To understand the core concept, however, simple and compound interest rates are the most straightforward examples of the future value calculation.
You can use the future value formula to calculate how your current savings may turn into a home down payment, car down payment, or funds used to pay tuition.
Formula and Calculation of Future Value
Future Value Using Simple Annual Interest
The future value formula assumes a constant rate of growth and a single up-front payment left untouched for the duration of the investment. The future value calculation can be done one of two ways, depending on the type of interest being earned. If an investment earns simple interest, then the FV formula is:
F
V
=
I
×
(
1
+
(
R
×
T
)
)
where:
I
=
Investment amount
R
=
Interest rate
T
=
Number of years
begin{aligned} &mathit{FV} = mathit{I} times ( 1 + ( mathit{R} times mathit{T} ) ) \ &textbf{where:}\ &mathit{I} = text{Investment amount} \ &mathit{R} = text{Interest rate} \ &mathit{T} = text{Number of years} \ end{aligned}
FV=I×(1+(R×T))where:I=Investment amountR=Interest rateT=Number of years
For example, assume a $1,000 investment is held for five years in a savings account with 10% simple interest paid annually. In this case, the FV of the $1,000 initial investment is $1,000 × [1 + (0.10 x 5)], or $1,500.
Future Value Using Compounded Annual Interest
With simple interest, it is assumed that the interest rate is earned only on the initial investment. With compounded interest, the rate is applied to each period’s cumulative account balance. In the example above, the first year of investment earns 10% × $1,000, or $100, in interest. The following year, however, the account total is $1,100 rather than $1,000; so, to calculate compounded interest, the 10% interest rate is applied to the full balance for second-year interest earnings of 10% × $1,100, or $110.
The formula for the FV of an investment earning compounding interest is:
F
V
=
I
×
(
1
+
R
)
T
where:
I
=
Investment amount
R
=
Interest rate
T
=
Number of years
begin{aligned}&mathit{FV} = mathit{I} times ( 1 + mathit{R})^T \&textbf{where:}\&mathit{I} = text{Investment amount} \&mathit{R} = text{Interest rate} \&mathit{T} = text{Number of years}end{aligned}
FV=I×(1+R)Twhere:I=Investment amountR=Interest rateT=Number of years
Using the above example, the same $1,000 invested for five years in a savings account with a 10% compounding interest rate would have an FV of $1,000 × [(1 + 0.10)5], or $1,610.51.
Bearish about the market? Future value can also handle negative interest rates to calculate scenarios such as how much $1,000 invested today will be worth if the market loses 5% each of the next two years.
Pros and Cons of Future Value
Future value can be useful in some situations. However, there are limitations to the calculation, and it may not be suitable for use in some cases.
Advantages of Future Value
- Future value allows for planning. A company or investor may know what they have today, and they may be able to input some assumptions about what will happen in the future. By combining this information, people can plan for the future as they understand their financial position. For example, a homebuyer attempting to save $100,000 for a down payment can calculate how long it will take to reach this savings by using future value.
- Future value makes comparisons easier. Let’s say an investor is comparing two investment options. One requires a $5,000 investment that will return 10% for the next 3 years. The other requires a $3,000 investment that will return 5% in year one, 10% in year 2, and 35% in year 3. The only way an investor will know which investment may make more money is by calculating the future values and comparing the results.
- Future value is easy to calculate due to estimates. Future value does not require sophisticated or real numbers. Because it is heavily reliant on estimates, anyone can use future value in hypothetical situations. For example, regarding the homebuyer above trying to save $100,000, that person can calculate the future value of their savings using their estimated monthly savings, estimated interest rate, and estimated savings period.
Disadvantages of Future Value
- Future value usually assumes constant growth. In the formulas above, only one interest rate is used. Although it is possible to calculate future value using different interest rates, calculations get more complex and less intuitive. In exchange for a simplified formula using only rate, a situation may have unrealistic parameters as growth may not always be linear or consistent year-over-year.
- Future value assumptions may not actually happen. Because future value is based on future assumptions, the calculations are simply estimates that may not truly happen. For example, an investor may have calculated the future value of their portfolio estimated the market would return 8% each year. When the market fails to produce that estimated return, the future value calculation from before is worthless.
- Future value may fail at comparisons. Future value simply returns a final dollar value for what something will be worth in the future. Therefore, there are some limitations when comparing two projects. Consider this example: an investor can choose to invest $10,000 for an expected 1% return or can choose to invest $100 for an expected 700% return. Looking at only future value, the first option would appear favorable because it is higher; it fails to consider the starting point of the initial investment.
Future Value Pros & Cons
Pros
-
Relies on estimates, therefore it is easy to calculate.
-
Future value calculations of lump sum or simple cashflows may be easy to calculate.
-
Future value can singlehanded determine whether an investor meets a target or goal.
-
The concept of future value can be applied to any cashflow, return, or investment structure.
Cons
-
Relies on estimates, therefore findings may be quickly invalidated.
-
Future value calculations of annuities or irregular cashflow may be difficult to calculate.
-
Future value by itself cannot be used to compare and choose between two mutually exclusive projects.
-
Most future value models assume constant rate growth which is often impractical.
Future Value vs. Present Value
The concept of future value is often closely tied to the concept of present value. Whereas future value calculations attempt to figure out the value of something in the future, present value attempts to figure out what something in the future will be worth today.
Both concepts rely on the same financial principles (i.e. discount or growth rates, compounding periods, initial investments, etc.). Each component is related and inherently feed into the calculation of the other. For example, imagine having $1,000 on hand today and expecting to earn 5% over the following year.
Future Value: $1,000 * (1 + 5%)^1 = $1,050
The future value formula could be reversed to determine how much something in the future is worth today. In other words, assuming the same investment assumptions, $1,050 has the present value of $1,000 today.
Present Value: $1,050 / (1 + 5%)^1 = $1,000
Therefore, by changing directions, future value can derive present value and vice versa. The future value of $1,000 one year from now invested at 5% is $1,050, and the present value of $1,050 one year from now assuming 5% interest is earned is $1,000.
Annuity vs. Annuity Due
When calculating future value of an annuity, understand the timing of when payments are made as this will impact your calculation. If payments are made at the end of a period, it is an ordinary annuity. If payments are made at the beginning of a period, it is an annuity due.
Example of Future Value
The Internal Revenue Service imposes a Failure to File Penalty on taxpayers who do not file their return by the due date. The penalty is calculated as 5% of unpaid taxes for each month a tax return is late up to a limit of 25% of unpaid taxes. An additional Failure to Pay penalty can also be assessed, and the IRS imposes interest on penalties.
If a taxpayer knows they have filed their return late and are subject to the 5% penalty, that taxpayer can easily calculate the future value of their owed taxes based on the imposed growth rate of their fee.
For example, consider if a taxpayer anticipates filing their return one month late. The taxpayer expects to have a $500 tax obligation. The taxpayer can calculate the future value of their obligation assuming a 5% penalty imposed on the $500 tax obligation for one month. In other words, the $500 tax obligation has a future value of $525 when factoring in the liability growth due to the 5% penalty.
Consider another example of a zero-coupon bond trading at a discount price of $950. The bond has two years left to maturity and has a target yield to maturity is 8%. If an investor is interested in knowing what the value of this bond will be in two years, they can simply calculate the future value based on the current variables. In two years, the future value of this bond will be $1,108.08 ($950 * (1 + 8%)^2). Through TreasuryDirect, the U.S. Department of Treasury bond website, investors can utilize calculators to estimate the growth and future value of savings bonds.
What Is Future Value?
Future value (FV) is a financial concept that assigns a value to an asset based on estimated variables such as future interest rates or cashflows. It may be useful for an investor to know how much their investment may be in five years given an expected rate of return. This concept of taking the investment value today, applying expected growth, and calculating what the investment will be in the future is future value.
How Do I Calculate Future Value?
There are several formulas to calculate future value. In all of them, the concept is the same: future value is calculated by taking cashflows and projecting them forward based on anticipated growth rates. Simple future value calculations regarding a single lump sum are easier to calculate (principal * (1 + rate) ^ periods), while future value calculations of annuities, varying cash flows, or varying interest rates are more complex.
What Is Future Value Used for?
Future value is used for planning purposes to see what an investment, cashflow, or expense may be in the future. Investors use future value to determine whether or not to embark on an investment given its future value. Future value can also be used to determine risk, see what a given expense will grow at if interest is charged, or be used as a savings target to understand whether enough money will be reserved given the current pace of savings and expected rate of return.
What Is the Future Value of an Annuity?
The future value of an annuity is the value of a group of recurring payments at a certain date in the future, assuming a particular rate of return, or discount rate. The higher the discount rate, the greater the annuity’s future value.
FV of an annuity is calculated as:
FV = PMT x [(1+r)n — 1)]/r
where:
- FV = Future value of an annuity stream
- PMT = Dollar amount of each annuity payment
- r = The discount (interest) rate
- n = Number of periods in which payments will be made
How Is Future Value Different From Present Value?
Future value takes a current situation and projects what it will be worth in the future. For example, future value would estimate the value of $1,000 today invested at 10% interest for 5 years. Alternatively, present value takes a future situation and projects what it is worth today. For example, present value would estimate how much money you would need to have today to invest at 10% for 5 years to end up with $1,000.
The Bottom Line
Future value (FV) is a key concept in finance that draws from the time value of money: a dollar today is worth relatively more than a dollar in the future. Using future value, once can estimate the value of that dollar at some point later in time, or the value of an investment or series of cash flows at that future date. In general, the future value of a sum of money today is calculated by multiplying the amount of cash by a function of the expected rate of return over the expected time period. Future value works in the opposite way as discounting future cash flows to the present value.
Расчет будущей стоимости
Простой процент.
Простым называется процент, который
начисляется только на изначальную сумму
инвестиций (кредита). По методике простого
процента доход в денежном выражении
определяется по формуле:
(1)
где SI
— доход, рассчитанный по простому
проценту, тыс. руб.; Ро — первоначальная
(базовая, исходная) величина инвестиций
(или принципал), тыс. руб.; i
— процентная ставка (цена денег) за
расчетный период, %; п — количество
временных периодов, за которые начисляется
простой процент на сумму первоначальной
инвестиции.
Будущую стоимость
(FV)
денег первоначального вклада можно
определить по формуле:
(2)
Расчет простых
процентов используется в следующих
операциях на практике:
— при оценке
доходности депозитных вкладов с
ежемесячной выплатой процентов;
— при оценке платы
за пользование ресурсами при выдаче
краткосрочных ссуд;
— в кредитных
договорах с периодическим погашением
основной суммы долга и выплатой процентов;
— при учете векселей;
— при оценке
доходности дисконтных ценных бумаг;
— при расчете
штрафных санкций за пользование чужими
финансовыми ресурсами и пр.
Однако данный
метод расчета доходов невыгодный.
Начисленные процентные доходы также
имеют стоимость, и инвестор вправе
рассчитывать на дополнительную выгоду
от того, что они находятся в обороте
должника (дебитора, заемщика денег).
Формула простого
процента может быть использована для
расчета любого показателя в ее составе:
1. для расчета
первоначальной суммы
2. для расчета суммы
процентных денег
3. для расчета
ставки процента
4. для расчета
периода
Сложный процент.
В основе практически всех финансовых
расчетов лежит метод начислений процентов
на проценты, или принцип сложного
процента. Формула расчета будущей
стоимости денег (в нашем примере это
стоимость депозитного вклада) строится
на основе известных параметров:
первоначальной инвестиции (Ро), годовой
ставки процента (i), количества лет (n).
Сумма денег на депозите на конец первого
года (FV1)
определяется по формуле 2 при n=
1:
Для того чтобы
рассчитать сумму денег на счете на конец
второго года (FV2)
по принципу сложного процента, в качестве
базовой следует рассматривать уже не
первоначальную инвестицию (Ро), а ту
сумму, которая образовалась на счете в
конце первого года, т.е. FV1:
(3)
Перепишем эту
формулу, подставив значение FV1,
т.е. выразив FV2
через первоначальную инвестицию (Ро):
(4)
В универсальном
виде для любых условий первоначальных
инвестиций, процентных ставок и количества
лет расчет будущей стоимости денег по
методу сложного процента будет
определяться по формуле:
(5)
Если величина
первоначальной инвестиции (Ро) может
иметь практически бесконечное количество
возможных значений, то второй сомножитель
формулы 5 – (1+i)n
, является
величиной, которую для удобства вычислений
можно стандартизировать. Для этого
разработаны специальные таблицы с
расчетом будущей стоимости 1 руб. при
различных вариантах сочетания ставок
процента и количества лет. Сокращенная
версия приведена в таблице 1.
Расчет будущей
стоимости 1 руб. при различных сочетаниях
ставок процента и количества лет: (1+i)n
= T1(i,n)
|
Период |
Ставка, |
|||
|
4 |
6 |
8 |
10 |
|
|
1 |
1,040 |
1,060 |
1,080 |
1,100 |
|
2 |
1,082 |
1,124 |
1,166 |
1,210 |
|
3 |
1,125 |
1,191 |
1,260 |
1,331 |
|
4 |
1,170 |
1,263 |
1,361 |
1,464 |
В упрощенном
варианте формулу расчета будущей
стоимости с учетом значений таблицы
записывают следующим образом:
(6)
где Т1(i, n)
— стоимость 1 руб. с начисленными сложными
процентами при заданных значениях i и
n,
которые приведены в таблице.
Многие финансовые
операции предполагают начисление
сложных процентов чаще одного раза в
год. Например, банки могут начислять
проценты по кредитам поквартально или
даже ежедневно. Для таких случаев будущая
стоимость денежных поступлений
рассчитывается по следующей формуле:
(7)
Формула расчета
сложных процентов может быть использована
для расчета любого входящего параметра:
1. первоначальная
сумма
2. периода
3. ставка процента
4. процентный доход
Будущая стоимость
серийных платежей (аннуитетов).
Широкое распространение в практике
финансовых расчетов имеют серийные
выплаты (или поступления) равновеликих
сумм в течение фиксированных интервалов
времени, иначе называемые аннуитетами.
Наибольшее распространение на практике
имею аннуитеты постнумерандо (обычные),
когда суммы денежных средств вносятся
в конце каждого периода.
Задачей финансовой
математики является определение будущей
стоимости серии равных периодических
выплат (FVAn)
в течение определенного временного
периода (n)
при заданной процентной ставке (i). Такой
расчет выполняется по формуле, основанной
на принципе геометрической прогрессии:
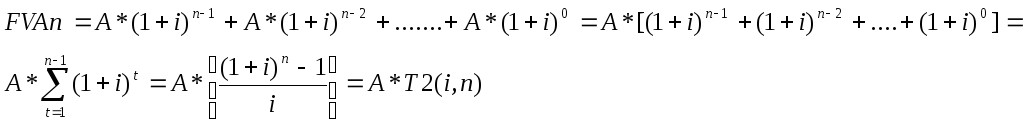
гдеА — равновеликая
сумма серийных платежей, тыс. руб.; Т2(i,
n)
— будущая стоимость серии равновеликих
периодических выплат в размере 1 руб. в
течение n
количества периодов, исчисленная по
i-й процентной ставке.
Сомножитель Т2(i,
n)
для удобства также стандартизирован в
виде специальной таблицы 3.
Расчет будущей
стоимости серии равновеликих периодических
выплат в размере 1 руб. в течение n
количества периодов при i-той
процентной ставке.
|
Период |
Ставка, |
|||
|
4 |
6 |
8 |
10 |
|
|
1 |
1,000 |
1,000 |
1,000 |
1,000 |
|
2 |
2,040 |
2,060 |
2,080 |
2,100 |
|
3 |
3,122 |
3,184 |
3,246 |
3,310 |
|
4 |
4,247 |
4,375 |
4,506 |
4,641 |
Эффективная
годовая процентная ставка.
В зависимости от
особенностей финансовых инструментов
и специфических договоренностей в
финансовых контрактах могут
предусматриваться различные схемы
начисления процентов. Как правило,
оговаривается номинальная годовая
процентная ставка. Однако, для проведения
сравнительного анализа эффективности
операций, необходимо определить
универсальный показатель доходности
для любой схемы начисления процентов.
Таким показателем является эффективная
годовая процентная ставка – которая
измеряет реальный относительный доход,
который получают в целом за год от
финансовой операции при использовании
данной схемы начисления.
Эффективная
процентная ставка – это годовая ставка
сложных процентов, которая дает тот же
результат, что и м-разовое начисление
процентов по номинальной ставке i.
Для определения
эффективной ставки используется
следующая формула:
Соседние файлы в папке 17-03-2014_13-30-06_1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Формула расчета будущей стоимости инвестиций
- Таблица расчета будущей стоимости инвестиций
- Будущая стоимость инвестиций: важные закономерности
- Резюме
Будущая стоимость инвестиций – это сумма, до которой возрастет первоначальный вклад с учетом капитализации на основе сложных процентов, в течение периода хранения средств на счете.
Расчет будущей стоимости инвестиций осуществляется с использованием стандартных формул.
Чтобы их усвоить, достаточно попрактиковаться на простом примере.
Допустим, у нас имеется вклад в размере 1000 долл. под 7% годовых. Будущая стоимость инвестиций в данном случае может быть рассчитана по следующей формуле:
Будущая стоимость на конец 1-го периода = 1000 долл. * (1 + 0,07) = 1070 долл.
В случае продления срока действия вклада на тех же условиях еще на год будущую стоимость вклада следует рассчитывать по той же формуле с учетом полученного результата:
Будущая стоимость на конец 2-го периода = 1070 долл. * (1 + 0,07) = 1144,9 долл.
Понятно, что этот процесс может быть продолжен сколь угодно долго.
Формула расчета будущей стоимости инвестиций
Было бы удобно, не производя промежуточных расчетов, сразу получать значения будущей стоимости денег (инвестиций) на некоторый период времени, располагая данными о [1] размере первоначального вклада и [2] размере процентной ставки.
Для этого выведем общую формулу.
Для сокращения записи обозначим будущую стоимость инвестиций на конец n-го периода буквой Sn, размер первоначального вклада – буквой N, размер процентной ставки – k.
Тогда наша формула примет вид:
Sn = N*(1+k/100)n.
В частности, будущая стоимость инвестиций на конец 2-го периода с учетом наших первоначальных данных будет рассчитана по формуле 1000 долл. * (1+7/100)2 = 1000 долл. * 1,1449 = 1144,9 долл., что соответствует полученному нами ранее результату.
Таблица расчета будущей стоимости инвестиций
На практике производить вручную приведенные выше расчеты бывает крайне утомительным.
Рассчитать будущую стоимость инвестиций на конец хотя бы 10-го периода способны разве что истинные фанаты счетного дела.
Попробуйте, к примеру, возвести в 10-ю степень число 1,07; лично я сразу начинаю искать калькулятор или что-то в этом роде…
До изобретения калькуляторов и компьютеров широко использовались таблицы с уже готовыми результатами.
На практике такие таблицы могут оказаться очень удобными в использовании.
Чтобы было понятно, о чем идет речь, предлагаю взглянуть на таблицу ниже:
Таблица содержит коэффициенты для 1 долл. (значения коэффициентов округлены до 3-го знака после запятой).
В частности, по истечению 2-го периода (года) при 7-процентной ставке размер вклада составит 1,145 долл. Если первоначальная сумма вклада составляла 1000 долл., то для расчета будущей стоимости вклада нужно его первоначальный размер умножить на соответствующий коэффициент из таблицы (1000 долл. * 1,145 = 1145 долл.).
Будущая стоимость инвестиций: важные закономерности
Внимательно присмотревшись к таблице, можно сделать несколько основополагающих выводов относительно формирования будущей стоимости инвестиций.
Во-первых, чем выше процентная ставка по вкладу, тем выше размер будущей стоимости.
Во-вторых, для каждой процентной ставки характерно увеличение размера будущей стоимости инвестиций с течением времени.
Наконец, в-третьих, коэффициент наращения будущей стоимости, как правило, всегда больше 1; он может быть равен 1 лишь в случае, когда процентная ставка равна 0.
В таком случае будущая стоимость инвестиций оказывается равной первоначальному вкладу, что случается, например, когда, вы просто одалживаете деньги на некоторый срок своим знакомым без взимания процентов за пользование одолженными средствами.
Конечно, использование таблиц не лишено недостатков.
Их расширение может представлять определенные трудности.
Если нам понадобится узнать размер капитала через 100 периодов, потребуется довольно обширная таблица, пользование которой окажется не таким уж простым делом.
На сегодняшний момент оптимальным следует признать использование так называемых инвестиционных калькуляторов, позволяющих в режиме онлайн производить соответствующие расчеты и мгновенно получать интересующие нас результаты.
Резюме
Сегодняшняя статья не охватывает всех аспектов, касающихся описания концепции сложных процентов и концепции будущей стоимости, а также связанных с этими концепциями расчетов.
Существует ряд формул, позволяющих рассчитывать будущую стоимость аннуитета (потока равных сумм денежных средств), приведенной стоимости, которые будет полезно усвоить каждому вдумчивому инвестору.
Но обо всем об этом мы поговорим в другой раз. Так что до скорой встречи и удачных инвестиций!