From Wikipedia, the free encyclopedia
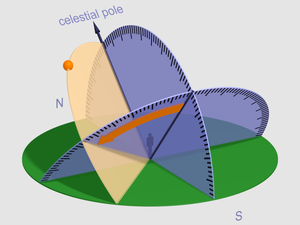
In astronomy and celestial navigation, the hour angle is the angle between two planes: one containing Earth’s axis and the zenith (the meridian plane), and the other containing Earth’s axis and a given point of interest (the hour circle).[1]
It may be given in degrees, time, or rotations depending on the application.
The angle may be expressed as negative east of the meridian plane and positive west of the meridian plane, or as positive westward from 0° to 360°. The angle may be measured in degrees or in time, with 24h = 360° exactly.
In celestial navigation, the convention is to measure in degrees westward from the prime meridian (Greenwich hour angle, GHA), from the local meridian (local hour angle, LHA) or from the first point of Aries (sidereal hour angle, SHA).
The hour angle is paired with the declination to fully specify the location of a point on the celestial sphere in the equatorial coordinate system.[2]
Relation with right ascension[edit]
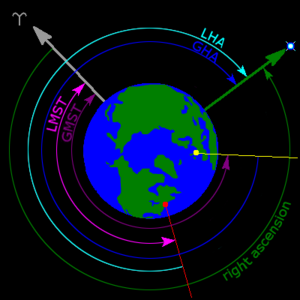
As seen from above the Earth’s north pole, a star’s local hour angle (LHA) for an observer near New York (red dot). Also depicted are the star’s right ascension and Greenwich hour angle (GHA), the local mean sidereal time (LMST) and Greenwich mean sidereal time (GMST). The symbol ʏ identifies the vernal equinox direction.
Assuming in this example the day of the year is the March equinox so the sun lies in the direction of the grey arrow then this star will rise about midnight. Just after the observer reaches the green arrow dawn comes and overwhelms with light the visibility of the star about six hours before it sets on the western horizon. The Right Ascension of the star is about 18h
The local hour angle (LHA) of an object in the observer’s sky is
or
where LHAobject is the local hour angle of the object, LST is the local sidereal time, 

Negative hour angles (−180° < LHAobject < 0°) indicate the object is approaching the meridian, positive hour angles (0° < LHAobject < 180°) indicate the object is moving away from the meridian; an hour angle of zero means the object is on the meridian.
Solar hour angle[edit]
Observing the Sun from Earth, the solar hour angle is an expression of time, expressed in angular measurement, usually degrees, from solar noon. At solar noon the hour angle is zero degrees, with the time before solar noon expressed as negative degrees, and the local time after solar noon expressed as positive degrees. For example, at 10:30 AM local apparent time the hour angle is −22.5° (15° per hour times 1.5 hours before noon).[4]
The cosine of the hour angle (cos(h)) is used to calculate the solar zenith angle. At solar noon, h = 0.000 so cos(h) = 1, and before and after solar noon the cos(± h) term = the same value for morning (negative hour angle) or afternoon (positive hour angle), so that the Sun is at the same altitude in the sky at 11:00AM and 1:00PM solar time.[5]
Sidereal hour angle[edit]
The sidereal hour angle (SHA) of a body on the celestial sphere is its angular distance west of the vernal equinox generally measured in degrees. The SHA of a star varies by less than a minute of arc per year, due to precession, while the SHA of a planet varies significantly from night to night. SHA is often used in celestial navigation and navigational astronomy, and values are published in astronomical almanacs.[citation needed]
See also[edit]
- Clock position
- List of orbits
Notes and references[edit]
- ^ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books. p. 729. ISBN 0-935702-68-7.
- ^ Explanatory Supplement (1992), p. 724.
- ^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 88. ISBN 0-943396-35-2.
- ^ Kreider, J. F. (2007). «Solar Energy Applications». Environmentally Conscious Alternative Energy Production. pp. 13–92. doi:10.1002/9780470209738.ch2. ISBN 9780470209738.
- ^ Schowengerdt, R. A. (2007). «Optical radiation models». Remote Sensing. pp. 45–88. doi:10.1016/B978-012369407-2/50005-X. ISBN 9780123694072.
Из
основной формулы времени для местного
меридиана получим
t*м
= tγм
— а*
или
t*м
= tγм
+
τ*
где
τ*=
360° — α*
Из
этой формулы видно, что для получения
местного часового угла звезды необходимо
предварительно получить часовой угол
точки Овна tγм,
что
выполняется по в указанном выше порядке.
Эфемериды
звезд τ*и
δ*
приводятся в разделе МАЕ, озаглавленном
«Видимые места звезд на … год». На левой
странице этого раздела помещены
значения τ*
по аргументам: название звезды и месяц
данного
года. Звезды приведены по их месту в
созвездии, например а Андромеды ит.
п. в порядке возрастания которое приведено
в крайней левой колонке с точностью
до 1м.
Таблицы
величин τ*
устроены
так, что градусы приводятся один раз
(впервой колонке), а минуты и их десятые
доли — на 1-е число каждого месяца.
Интерполирование τ*на
данное число производится между колонками
«в уме»; впрочем часто им можно
пренебрегать. На правой странице в том
же порядке приведены склонения звезд
по тем же номерам списка звезд, что и на
левой странице, и, кроме того, по
собственному названию звезды, если оно
имеется. В крайней правой колонке
приведены «величины» звезд, характеризующие
их яркости
В
начале этого раздела приводятся списки
латинских и
русских
названий созвездий и звезд; латинские
названия нужны при работе со звездным
глобусом.
Для
облегчения выборки координат звезд в
МАЕ дается вкладыш, на котором помещены
значения τ
и δ
основных
50 навигационных звезд и Полярной через
10 суток. В отличие от основных таблиц,
па вкладыше значения τ
и δ
каждой
звезды помещены рядом, причем градусы
приведены вверху колонки, а минуты и их
десятые — в колонке по датам. Из этой
таблицы координаты звезд (за исключением
Полярной) получаются всегда с точностью
до 0′,1 без интерполяции.
Следовательно,
получение часового угла звезды
производится выборками из двух
разделов: ежедневных таблиц и таблиц
для звезд (или вкладыша). В общем виде
формула для будет:
t*м
=
tγт
+ Δtγ*Т
±
λΕ/W
+ τ*
.
4.3
Получение
часовых углов и склонений Солнца
Для
получения часового угла центра истинного
Солнца по гринвичскому вемени Тгр
воспользуемся
основной формулой времени,написанной
для Ο+
и О. и меридиана Гринвича, т. е
Sгр
= tгрo
+ αΟ
Sгр=
t
Oгр
+
α*
откуда
tOгр
= tOгр
+ αΟ
–αΟ
или,
учитывая,
что Тгр
=tOгр
±
12ч, получим:
tгрO=Тгр±
12*
+ αΟ—αΟ
(9.7)
где
аΟ
—
αΟ
= η
—уравнение времени в данный момент.
По
этой формуле предвычислены значения
часовых углов Солнца
(tтО)
на целые часы Тгр
и
помещены в ежедневных таблицах МАЕ. Для
интерполирования часового угла на
промежуточные значения Тгр
в
МАЕ для всех светил (кроме звезд) применен
одинаковый прием введения двух всегда
положительных поправок:/-постоянной
поправки, зависящей только отΔТгр
и
небольшой переменной в течение года
поправки, зависящей от значения а светила
на данный день и час. Последняя поправка
получается интерполированием так
называемой квазиразности
Δ,
приводимой
в МАЕ внизу колонки часовых углов
(для
Луны — рядом с tсгр Для
Солнца формула получения tогр
на данный момент Тгр
будет
иметь вид:
tогр
= tогр
+ [ΔΤгр
+ (ΔαΟ
-ΔαΟтах
)/60мин
* ΔТгрмин]°
+
{(Δαомах-Δαо)/60min*ΔТгрмин]0
гдеΔTгр—избыток
Тгр
сверх
целого часа;
ΔαΟ
–ΔαΟмах
= -0’3
—
постоянная
поправка, равная наибольшему изменению
уравнения времени в году (за час ΔαΟ
=2′,46, а
ΔαΟмах
= 2′,78);
ΔαΟмах
—
ΔαΟ
= Δ
—
квазиразность
для Солнца, величина, изменяющаяся
от 0′,0 до 0′,5 (так как наименьшее Δа0
= 2′,24 в час) и всегда положительная.
Следовательно,
квазиразностью
Δ
в
МАЕ
называется
искусственная разность часовых
изменений прямых восхождений —
наибольшего возможного изменения и
изменения
за данный час (Δα.свст).
Квазиразность
можно представить и как разность
изменения величины часового угла (
Δt)
за
данный час и минимального изменения
(Δtmin)
для
данного светила, например для Солнца
Δ=Δt—14°59′,7.
Второй
член формулы представляет основную
поправку Δ1t
часового угла Солнца, равную 14°59/,7
за час, и выбирается по.ΔТгр
из
второй колонки основной интерполяционной
таблицы (страница отыскивается по
минутам,-строка — по секундам).
Третий
член Δ2
t
формулы (9.8) выбирается из средней колонки
этих же таблиц по Δ
и минуте Δ.Тгр.
В
общем виде tгрО
получается по формуле
tгрO=tγO+Δ1t+Δ2t
Местный
часовой угол Солнца получится добавлением
к этой
формуле
долготы,
т.
е.
tгрO
= tγ
O + Δ1
t + Δ2
t
± λΕ/W
Склонение
Солнца выбирается также из ежедневных
таблиц и интерполируется по средней
колонке основных таблиц, на основании
следующей формулы линейного
интерполирования
ΔδΟ
= Δ/60
*ΔΤ
гр
где
Δ
—
часовое
изменение склонения Солнца, приводимое
с его знаком внизу колонки склонений.
Соседние файлы в папке Астрономия лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье мы будем решать задачи, связанные со временем в астрономии. Научимся определять звездное время, часовые углы. Увидим, что в разных местах одновременно время — разное.
Напомню основные положения прошлой статьи:
Звездное время измеряется часовым углом
точки весеннего равноденствия и поэтому всегда
. У небесного светила с прямым восхождением
часовой угол
Звездное время в пункте с географической долготой
связано со звездным гринвичским временем
равенством
причем отсчитывается к востоку от Гринвича и выражается в часах, минутах и секундах времени. Для перевода градусных единиц в единицы времени существуют таблицы, можно воспользоваться примером расчета выше.
В один и тот же физический момент звездное время и
в двух пунктах различается на разность географической долготы
и
этих пунктов, т. е.
Используемые в практической жизни средние солнечные сутки продолжительнее звездных суток приблизительно на Зм56с.
Местное среднее время
где — уравнение времени, a
—истинное солнечное время, измеряемое часовым углом Солнца, увеличенным на 12ч, т. е.
Местное среднее время и
двух пунктов связано между собой равенством:
а со средним гринвичским временем (называемым всемирным временем) — равенством
В практической жизни используется либо поясное время
либо декретное время
где — номер часового пояса, равный целому числу часов.
Для двух пунктов, расположенных в разных часовых поясах n1 и n2,
Если система счета времени не указана, то всегда подразумевается время, действующее на данной территории.
Задача 1.
Определить звездное время в моменты верхней и нижней кульминации звезды Фомальгаута ( Южной Рыбы), прямое восхождение которой 22 ч 54 м 53 с.
В момент верхней кульминации всегда , поэтому
22 ч 54 м 53 с.
В нижней кульминации всегда 12 ч, поэтому
22 ч 54 м 53 c +12 ч=34 ч 54 м 53 с- 24 ч=10 ч 54 м 53 с.
Ответ: в верхней кульминации 22 ч 54 м 53 с, в нижней
10 ч 54 м 53 с.
Задача 2.
Найти звездное время в моменты, в которые часовой угол звезды Ригеля ( Ориона) соответственно равен (-3 ч 17 м 43 с) и 1 ч 42 м 29 с. Прямое восхождение этой звезды 5 ч 12 м 08 с.
-3 ч 17 м 43 с+ 5 ч 12 м 08 с=1 ч 54 м 25 с
1 ч 42 м 29 с+ 5 ч 12 м 08 с=6 ч 54 м 37 с
Ответ: 1 ч 54 м 25 с,
6 ч 54 м 37 с
Задача 3.
Определить звездное время в пунктах с географической долготой 2 ч 13 м 23 с и в момент, когда в пункте с долготой 4 ч 37 м 11 с звезда Кастор (
Близнецов) находится в верхней кульминации. Прямое восхождение Кастора 7 ч 31 м 25 с.
Когда звезда в верхней кульминации, ее часовой угол равен 0. Поэтому звездное время
7 ч 31 м 25 с.
Время в пункте с нулевой долготой может быть найдено так:
7 ч 31 м 25 с-4 ч 37 м 11 с =2 ч 54 м 14 с.
Теперь добавим к этому звездному времени долготы тех мест, которые нас интересуют:
2 ч 54 м 14 с+2 ч 13 м 23 с=5 ч 07 м 37 с
Переведем во время долготу второго места:
5ч 39 м 52 с, я для этого пользовалась таблицей.
Вычисляем звездное время в этом пункте:
2 ч 54 м 14 с+5ч 39 м 52 с =8ч 34 м 06 с.
Ответ: 5 ч 07 м 37 с,
8 ч 34 м 06 с.
Задача 4.
Решить предыдущую задачу для тех же пунктов, но для момента времени, в который звезда Капелла ( Возничего) находится в нижней кульминации в Иркутске (
6 ч 57 м 05 с). Прямое восхождение Капеллы 5 ч 13 м 00 с.
В нижней кульминации часовой угол звезды 12 ч. Поэтому
12+5ч 13 м 00с=17 ч 13 м 00 с.
Так как Иркутск восточнее Гринвича, то
17 ч 13 м 00 с -6 ч 57 м 05 с =10 ч 15 м 55 с.
Теперь добавим к этому звездному времени долготы тех мест, которые нас интересуют:
10 ч 15 м 55 с +2 ч 13 м 23 с=12 ч 29 м 18 с
Переведем во время долготу второго места:
5ч 39 м 52 с, я для этого пользовалась таблицей.
Вычисляем звездное время в этом пункте:
10 ч 15 м 55 с +5ч 39 м 52 с =15ч 55 м 47 с.
Ответ: 12ч 29 м 18 с,
15 ч 55 м 47 с.
Задача 5.
Вычислить часовые углы звезд Алголя ( Персея) и Альтаира (
Орла) в 8 ч 20 м 30 с по звездному времени. Прямое восхождение этих звезд соответственно равно 3 ч 04 м 54 с и 19 ч 48 м 21 с. Часовые углы выразить в градусных единицах.
8 ч 20 м 30 с-3 ч 04 м 54 с=5 ч 15 м 36 с
8 ч 20 м 30 с-19 ч 48 м 21 с =-11 ч 27 м 51 с
Добавим 24 часа, чтобы часовой угол был положительным:
-11 ч 27 м 51 с +24 ч 00 м 00 с=12 ч 32 м 09 с.
Осталось перевести результаты в единицы времени:
5 ч 15 м 36 с=
12 ч 32 м 09 с=
Ответ: 5 ч 15 м 36 с,
,
12 ч 32 м 09 с,
.
Задача 6.
Прямое восхождение звезды Миры ( Кита) 2 ч 16 м 49 с, Сириуса (
Большого Пса) 6 ч 42 м 57 с и Проциона (
Малого Пса) 7 ч 36 м 41 с. Чему равны часовые углы этих звезд в моменты верхней и нижней кульминации Сириуса?
Для верхней кульминации Сириуса , для нижней —
12 ч. Звездное время для верхней кульминации
6 ч 42 м 57 с
Для нижней
18 ч 42 м 57 с
Определяем часовые углы звезд Миры
6 ч 42 м 57 с-2 ч 16 м 49 с=4 ч 26 м 08 с
18 ч 42 м 57 с -2 ч 16 м 49 с=16 ч 26 м 08 с
И Проциона:
6 ч 42 м 57 с-7 ч 36 м 41 с=-0 ч 53 м 44 с
18 ч 42 м 57 с -7 ч 36 м 41 с=11 ч 06 м 16 с
Ответ: в верхней кульминации Сириуса его часовой угол ч, у Миры
4ч 26 м 08 с, у Проциона
-0 ч 53 м 44 с, в нижней кульминации Сириуса его часовой угол 12 ч, у Миры
16 ч 26 м 08 с, у Проциона
11 ч 06 м 16 с.
Задача 7.
Найти часовые углы звезд Кастора ( Близнецов) и Шеата (
Пегаса) в момент, когда часовой угол звезды Беги (
Лиры) равен 4ч15м10с. Прямое восхождение Кастора 7 ч 31 м 25 с, Беги 18 ч 35 м 15 с и Шеата 23 ч 01 м 21 с.
Найдем звездное время по данным для Беги:
4 ч 15 м 10 с+18 ч 35 м 15 с=22 ч 50 м 25 с.
Теперь с легкостью рассчитываем часовые углы Кастора:
22 ч 50 м 25 с-7 ч 31 м 25 с=15ч 19 м 0 с
И Шеата:
22ч 50м 25 с-23 ч 01 м 21 с =-0ч 10 м 56 с
Или 23 ч 49 м 04 с.
Ответ: часовой угол Кастора 15ч 19 м 0 с, Шеата 23 ч 49 м 04 с.
Задача 8.
Часовой угол звезды Миры ( Кита) в Гринвиче равен 2ч16м47с. Определить в этот момент звездное время в пунктах с географической долготой 2ч 03 м 02 с и
. Прямое восхождение Миры 2 ч 16 м 49 с.
Переведем долготу второго места во временные единицы:
=3ч 20 м 00 с+16м+ 2 м 56 с+ 2 с=3 ч 38 м 58 с.
Звездное время в Гринвиче равно
2 ч 16 м 47 с+2 ч 16 м 49 с=4ч 33 м 36 с
Оба места расположены восточнее Гринвича, поэтому
4ч 33 м 36 с+2ч03м02с=6ч 36 м 38 с
4ч 33 м 36 с+3 ч 38 м 58 с =8ч 12 м 34 с
Ответ: 6ч 36 м 38 с,
8ч 12 м 34 с.
Задача 9.
Найти звездное время и часовой угол звезды Мицара ( Большой Медведицы) в Гринвиче и в пункте с географической долготой 6 ч 34 м 09 с в тот момент, когда в Якутске (
8 ч 38 м 58 с) часовой угол звезды Альдебарана (
Тельца)
. Прямое восхождение Мицара 13 ч 21 м 55 с, а Альдебарана 4 ч 33 м 03 с.
Переводим для начала часовой угол Альдебарана во временные единицы:
=20ч+1 ч 20 м+36 м+2м 56с =21ч 58м 56 с.
Звездное время в Якутске:
21 ч 58 м 56 с+4 ч 33 м 03 с=26 ч 31 м 59 с=2 ч 31 м 59 с.
Теперь, зная долготу Якутска, определяем звездное время в Гринвиче. Якутск восточнее Гринвича, поэтому
2 ч 31 м 59 с-8 ч 38 м 58 с=26 ч 31 м 59 с-8 ч 38 м 58 с=17 ч 53 м 01 с
Часовой угол Мицара в Гринвиче равен
17 ч 53 м 01 с-13 ч 21 м 55 с=4 ч 31 м 06 с
Теперь из Гринвича смещаемся в пункт с долготой 6ч34м09с:
17 ч 53 м 01 с+6 ч 34 м 09 с=24 ч 27 м 10 с=0 ч 27 м 10 с.
Часовой угол Мицара здесь равен
0 ч 27 м 10 с -13 ч 21 м 55 с=24 ч 27 м 10 с-13 ч 21 м 55 с=11 ч 05 м 15 с.
Ответ: звездное время в Гринвиче 17 ч 53 м 01 с, часовой угол Мицара
4 ч 31 м 06 с, звездное время в месте с долготой 6 ч 34 м 09 с:
0 ч 27 м 10 с, часовой угол Мицара здесь равен
11 ч 05 м 15 с.
Задача 10.
Какое прямое восхождение у звезд, находящихся в верхней и нижней кульминации в двух различных пунктах наблюдения, если в одном из них, расположенном восточнее другого на , часовой угол звезды Проциона (
Малого Пса) равен (-2 ч 16 м 41 с)? Прямое восхождение Проциона 7 ч 36 м 41 с.
Звездное время в первом пункте:
-2 ч 16 м 41 с+7 ч 36 м 41 с=5 ч 20 м 00 с
Если звезды в верхней кульминации, их часовые углы равны 0:
5ч 20м 00 с
А если в нижней, то 12 ч, тогда
5ч 20м 00 с-12ч=-6 ч 40 м 00с=17 ч 20 м 00 с
Теперь перебираемся во второй пункт, который по условию задачи западнее. Давайте установим, насколько: = 2 ч+24 м+2 м 48 с=2ч 26 м 48 с.
Звездное время в более западном пункте меньше на его долготу:
5 ч 20 м 00 с-2 ч 26 м 48 с=2 ч 53 м 12 с
Теперь вычислим прямое восхождение звезд в верхней кульминации:
2 ч 53 м 12 с
2 ч 53 м 12 с -12ч=-9 ч 06 м 48 с=14 ч 53 м 12 с
Ответ: в верхней кульминации в первом пункте 5 ч 20 м 00 с, в нижней —
17 ч 20 м 00 с, в верхней кульминации во втором пункте
2 ч 53 м 12 с , в нижней
14 ч 53 м 12 с.