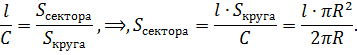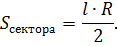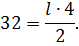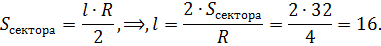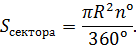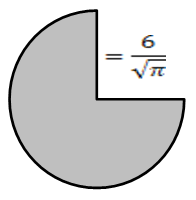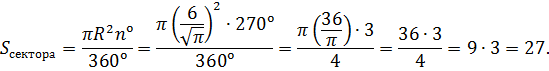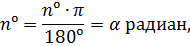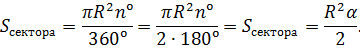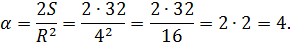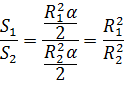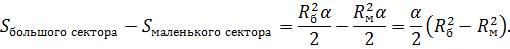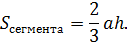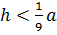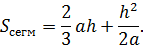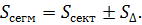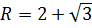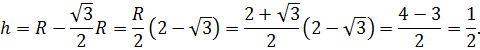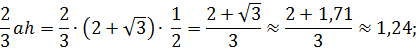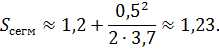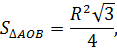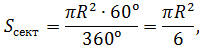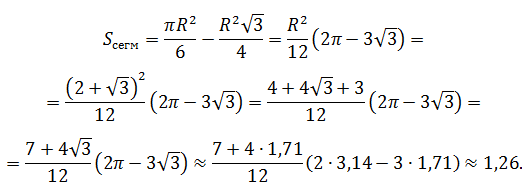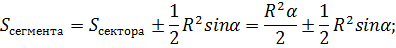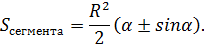Площадь круга и его частей. Длина окружности и ее дуг
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
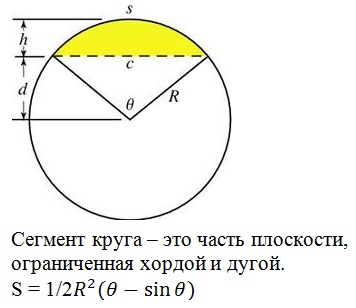
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей

где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах

если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга
Площадь сектора

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь сегмента

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах

если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
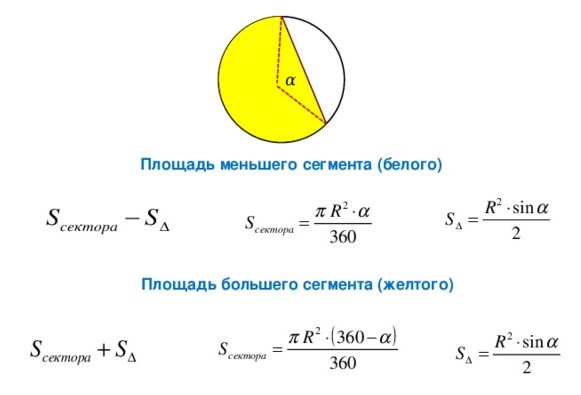
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
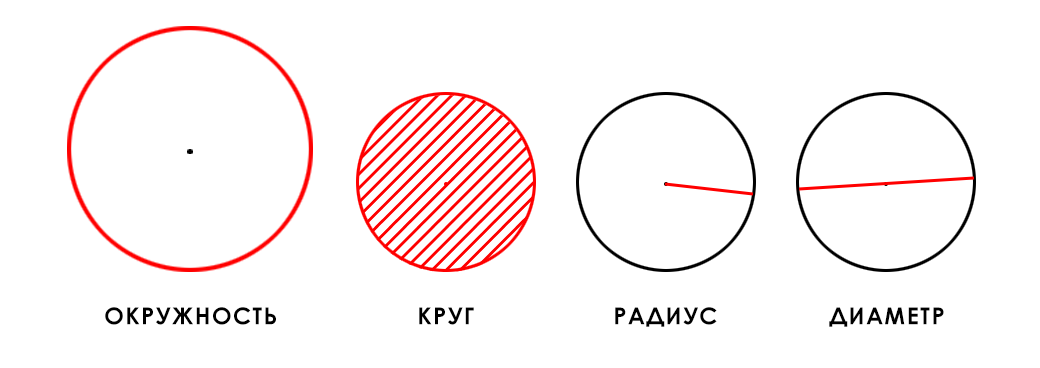
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Площадь сектора круга — формулы и примеры расчетов
Выполняя инженерные расчёты при проектировании различных объектов строительства, создании роботов, автоматизированных систем, станков, машин, самолётов, ракет, современных средств вооружения часто бывает необходимо найти площадь сектора круга.
Геометрия помогает при этом решать задачи на нахождение центра тяжести (центр масс), вычислять его координаты для плоских пластин, имеющих, в частности, форму правильного многоугольника.
Измерять и вычислять величины считается базовым умением. Оно включено в первую часть профильной программы выпускного экзамена ЕГЭ и ОГЭ по математике.
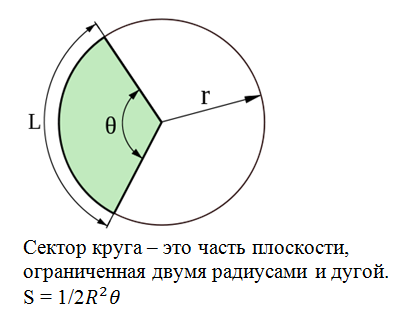
Сектор круга
Существует несколько определений, каждое из которых отличается только формулировкой, не меняющей подход к рассмотрению понятия:
Часть плоскости, ограниченная центральным углом и соответствующей дугой окружности.
Часть круга, заключённая между двумя радиусами.
Часто эту формулировку заменяют похожей, описывающей построение непосредственно: часть круга, лежащего внутри соответствующего центрального угла.
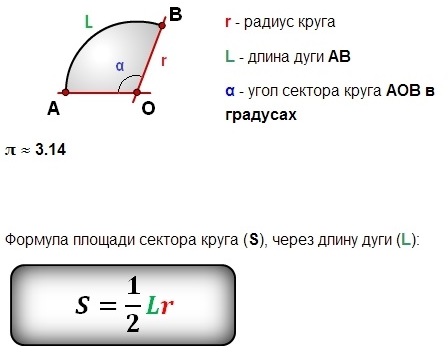
Площадь сектора круга через радиус и длину дуги
Пусть известны радиус круга R, длина дуги l. Как в этом случае определить площадь сектора, стягиваемого данной дугой?
Для ответа на вопрос понадобится формула нахождения длины окружности:
Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.
Поскольку отношения постоянны, то для ответа на поставленный вопрос достаточно найти отношение части к целому, затем умножить полученный результат на площадь круга S = πR 2 .
После сокращения дроби получают формулу:
Примеры решения задач
Задача №1
Найти площадь сектора круга радиусом 2 см, имеющего длину дуги 4 см.
Подставляя имеющиеся величины в формулу, получаем:
Sсект = (4 * 2) / 2 = 4.
Ответ: Sсект = 4 см 2 .
Задача №2
Подставив известные данные в формулу, получим:
Тот же результат получился бы при первоначальной работе в «общем виде»:
Площадь сектора круга через радиус и угол сектора
Если известна градусная мера центрального угла (n°), то, находя отношение её к полному кругу (к 360º), также умножают результат на площадь круга:
Задача №3
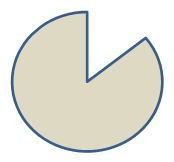
Чему равна площадь фигуры, изображённой на рисунке?
Центральный угол изображённого сектора равен
Подставляя в формулу величины, несложно получить искомый результат:
Ответ: Sсект = 27 см 2 .
Также аналогичным образом решаются обратные задачи.
Площадь сектора круга через угол сектора в радианах
Пусть центральный угол задан своей радианной мерой. Учитывая, что
несложно получить искомую формулу:
Задача №4
Чему равен центральный угол сектора в радианах (рад.), если его площадь равна 32, а радиус – 4?
Выразив α, затем подставив числовые данные, легко получить результат:
Благодаря этой формуле, несложно доказать, что площади двух секторов с равными центральными углами относятся как квадраты радиусов соответствующих окружностей:
С другой стороны, площадь части кольца находится из условия:
Сегмент круга
Существует два подхода к определению понятия:
Геометрическая фигура, являющаяся общей частью круга и полуплоскости, называется сегментом круга.
Часть плоскости, заключённая между хордой и окружностью.
Оба определения характеризуют один и тот же объект с разных сторон, выражая, по сути одно и то же.
Иногда проводится описательное построение. В этом случае второй вариант быстрее приводит к данному термину.
Площадь сегмента круга по хорде и высоте
Пусть градусная мера ограничивающей дуги мала, длина хорды равна a, h — высота сегмента (перпендикуляр, опущенный из точки на окружности к середине хорды). Примечание: часто высота сегмента называется «стрелкой».
Тогда можно приближённо считать, что
Погрешность такого вычисления уменьшается вместе с отношением
В частности, когда дуга содержит угол, меньший 50º, то есть,
погрешность оказывается менее 1%.
Более точной является формула для любого сегмента меньшего полукруга:
Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.
Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).
Отсюда следует, что
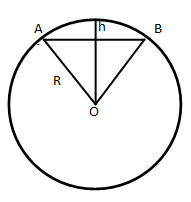
Задача №5
Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а
Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB. Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса).
Отсюда следует, что:
Площадь по первой формуле будет приблизительно равна
Применяя точную формулу и учитывая, что
Ответ: Sсегм = 1,26 см 2 .
Площадь сегмента круга через синус угла
Рассматривая точную формулу, площадь треугольника можно находить, используя половину произведения сторон на синус угла между ними. А значит:
Многие вычисления помогает провести онлайн калькулятор. Достаточно ввести исходные данные и запросить результат.
http://skysmart.ru/articles/mathematic/ploshad-kruga
http://nauka.club/matematika/geometriya/ploshchad-sektora-kruga.html

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
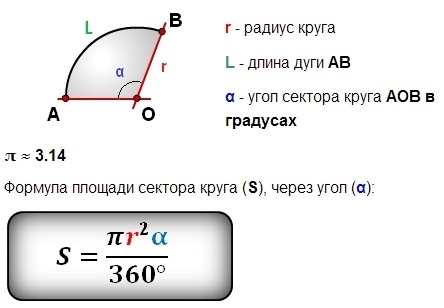
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент — все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Периметр круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Периметр круга
Чтобы посчитать периметр круга просто воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
его радиус ?
Ответ:
0
Каков периметр круга (L) если его радиус r ?
Формула
L = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
его диаметр ?
Ответ:
0
Каков периметр круга (L) если его диаметр d?
Формула
L = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
его площадь ?
Ответ:
0
Каков периметр круга (L) если его площадь S?
Формула
L = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 8 см2, то его периметр ≈ 10 см.
См. также
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
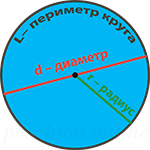
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
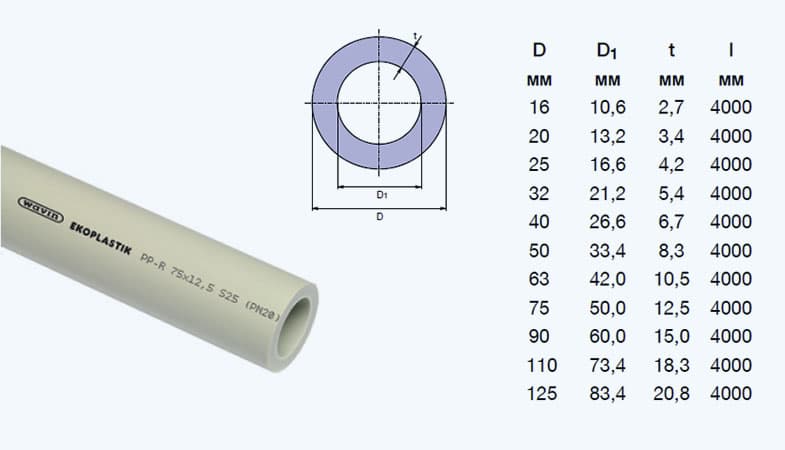
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Сегмент — это геометрическая фигура, которая получается путем отсечение части круга хордой.
Онлайн-калькулятор площади сегмента круга
Находится эта фигура между хордой и дугой круга.
Это отрезок, лежащий внутри круга и соединяющий две произвольно выбранные точки на нем.
При отсечении части круга хордой можно рассмотреть две фигуры: это наш сегмент и равнобедренный треугольник, боковые стороны которого — радиусы круга.
Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.
Площадь сегмента можно найти несколькими способами. Остановимся на них более подробно.
Формула площади сегмента круга через радиус и длину дуги круга, высоту и основание треугольника
S=12⋅R⋅s−12⋅h⋅aS=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot a
RR — радиус круга;
ss — длина дуги;
hh — высота равнобедренного треугольника;
aa — длина основания этого треугольника.
Дан круг, его радиус, численно равный 5 (см.), высота, которая проведена к основанию треугольника, равная 2 (см.), длина дуги 10 (см.). Найти площадь сегмента круга.
Решение
R=5R=5
h=2h=2
s=10s=10
Для вычисления площади нам не хватает только основания треугольника. Найдем его по формуле:
a=2⋅h⋅(2⋅R−h)=2⋅2⋅(2⋅5−2)=8a=2cdotsqrt{hcdot(2cdot R-h)}=2cdotsqrt{2cdot(2cdot 5-2)}=8
Теперь можно вычислить площадь сегмента:
S=12⋅R⋅s−12⋅h⋅a=12⋅5⋅10−12⋅2⋅8=17S=frac{1}{2}cdot Rcdot s-frac{1}{2}cdot hcdot a=frac{1}{2}cdot 5cdot 10-frac{1}{2}cdot 2cdot 8=17 (см. кв.)
Ответ: 17 см. кв.
Формула площади сегмента круга по радиусу круга и центральном углу
S=R22⋅(α−sin(α))S=frac{R^2}{2}cdot(alpha-sin(alpha))
RR — радиус круга;
αalpha — центральный угол между двумя радиусами, стягивающий хорду, измеряющийся в радианах.
Найти площадь сегмента круга, если радиус круга равен 7 (см.), а центральный угол 30 градусов.
Решение
R=7R=7
α=30∘alpha=30^{circ}
Переведем сначала угол в градусах в радианы. Поскольку πpi радиан равен 180 градусов, то:
30∘=30∘⋅π180∘=π630^{circ}=30^{circ}cdotfrac{pi}{180^{circ}}=frac{pi}{6} радиан. Тогда площадь сегмента:
S=R22⋅(α−sin(α))=492⋅(π6−sin(π6))≈0.57S=frac{R^2}{2}cdot(alpha-sin(alpha))=frac{49}{2}cdotBig(frac{pi}{6}-sinBig(frac{pi}{6}Big)Big)approx0.57 (см. кв.)
Ответ: 0.57 см. кв.
Не знаете, как выполнить работу с нахождением площади сегмента круга? Наши эксперты помогут вам решить контрольную по геометрии онлайн!