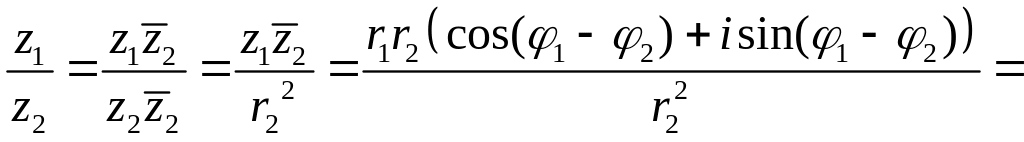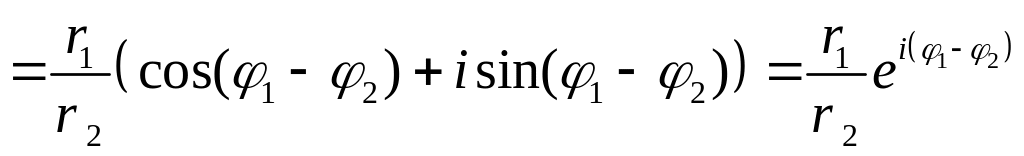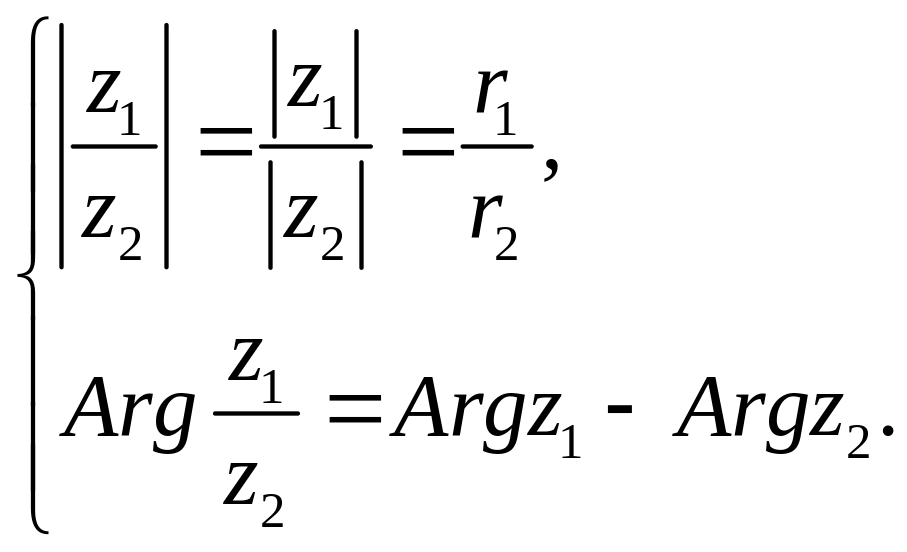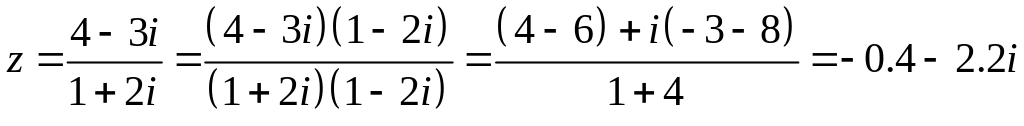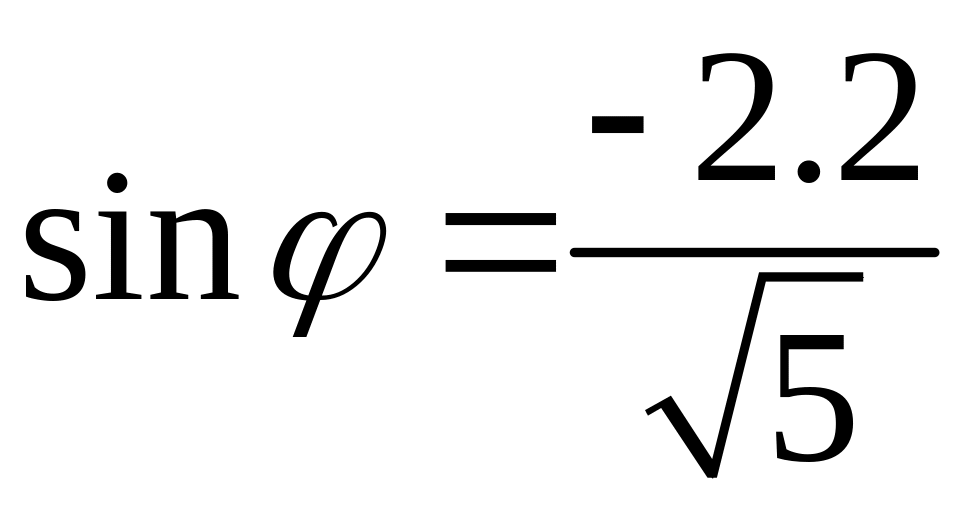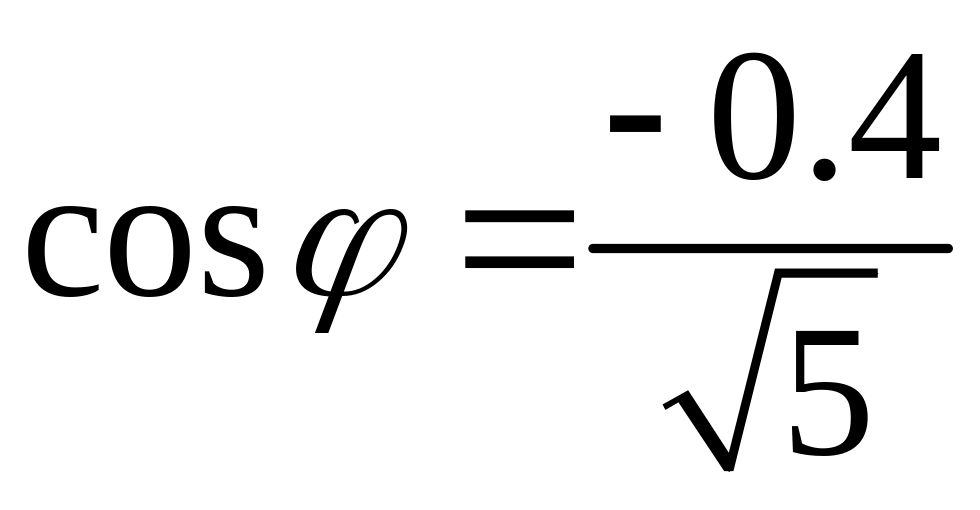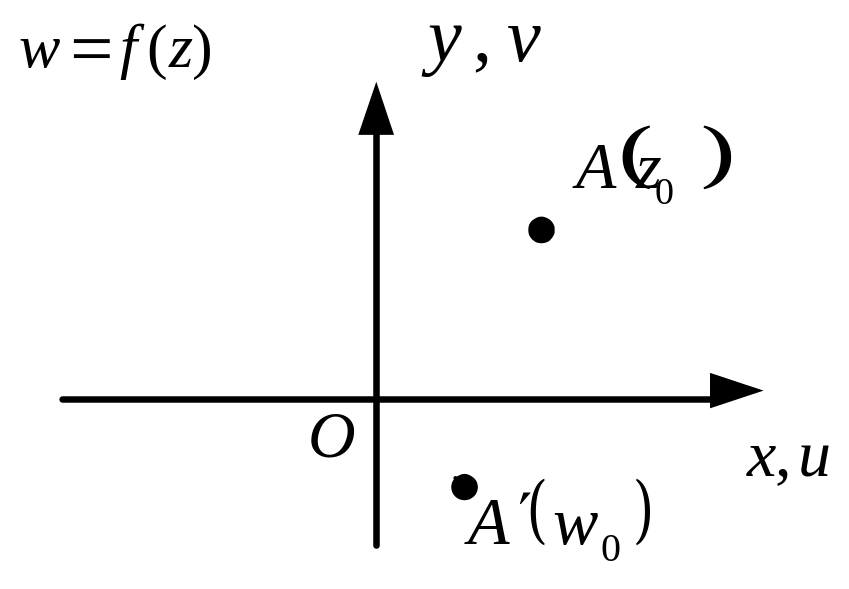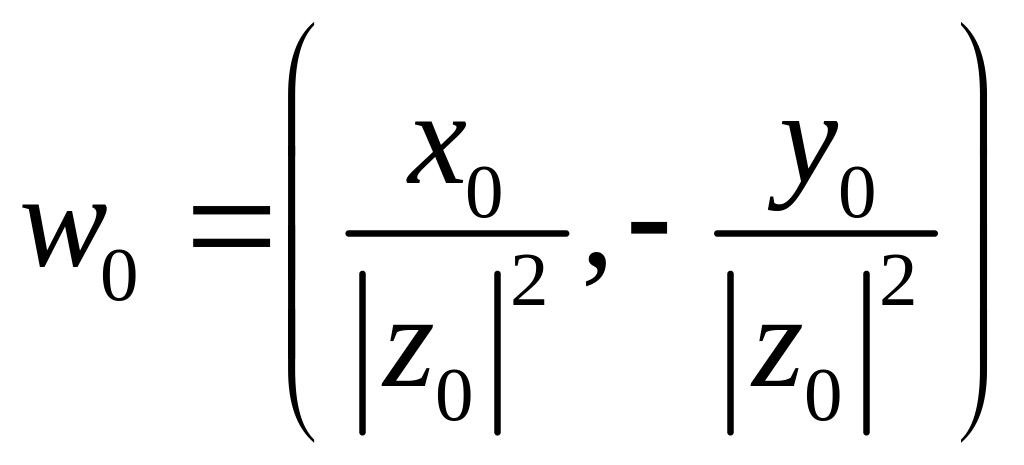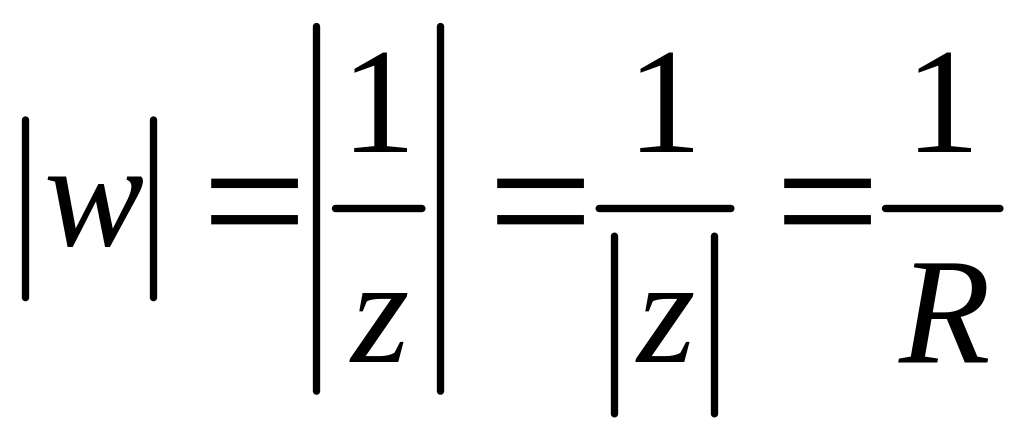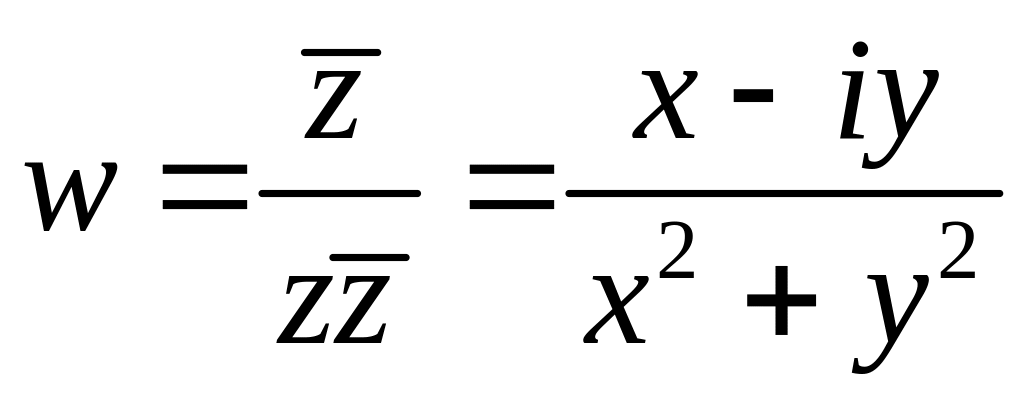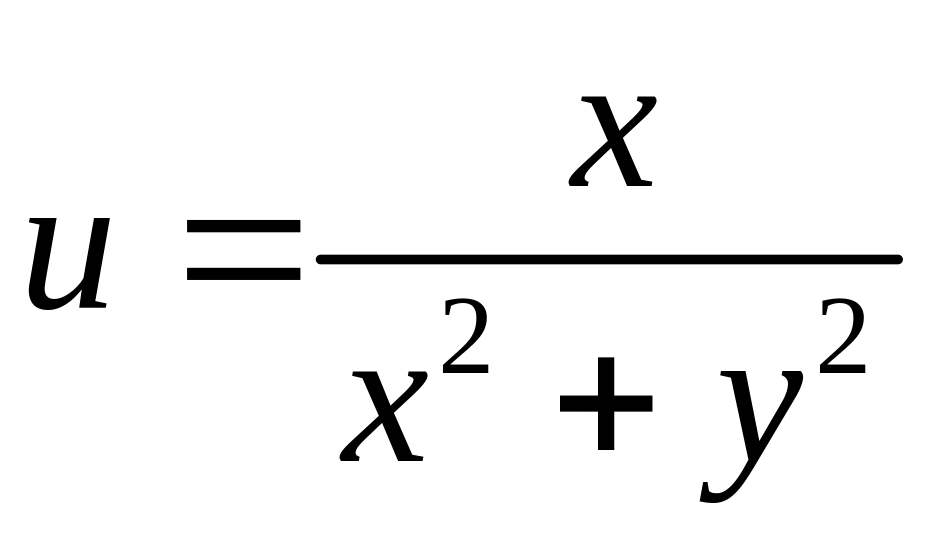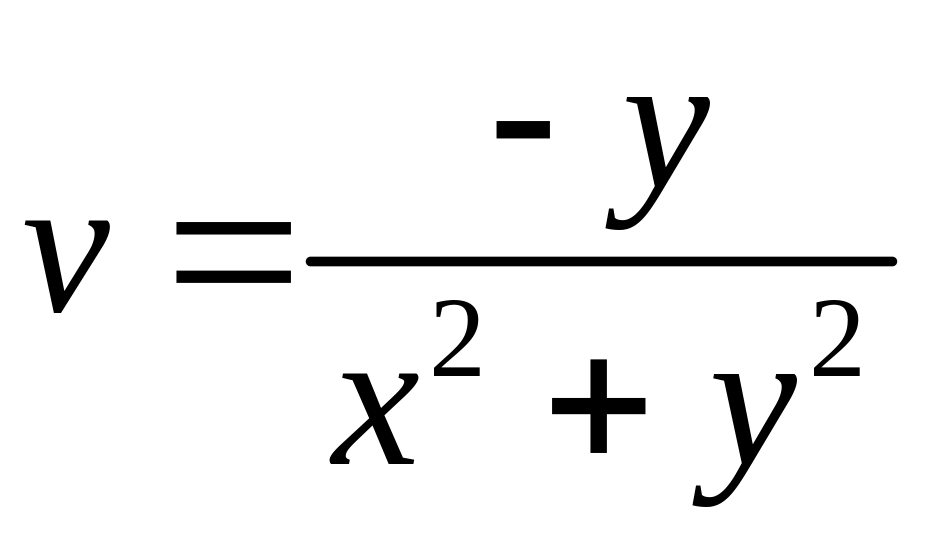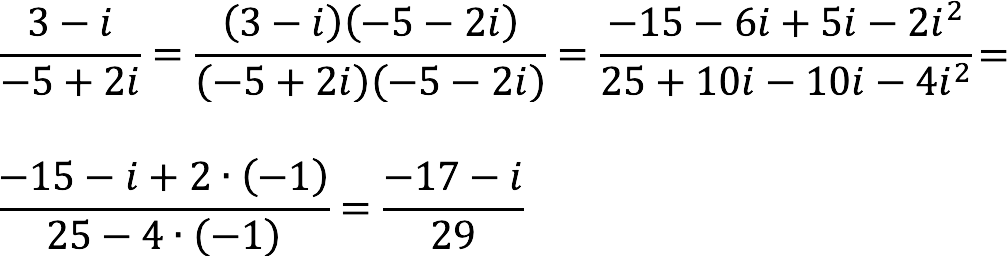Как найти частное число в показательной форме - Исправление недочетов и поиск решений вместе с Examum.ru

Частное комплексных чисел в тригонометрической и показательной формах

Для комплексных
чисел

частное

может быть записано в следующем виде

,
откуда следует, что модуль
частного двух комплексных чисел равен
отношению модулей делимого и делителя,
а главное значение
аргумента
частного с точностью до

равно разности
аргументов делимого и делителя.

(9)

Пример 18.
Представить в показательной форме числа

а)

; б)

.

Решение. а)

.
Для этого числа

.

,
поэтому

.

б)
Найдем модуль
и аргумент числа

,
предварительно представив его в
алгебраической форме.

.

— алгебраическая форма данного числа и

,

,

.

Так как действительная
и мнимая части числа

отрицательны, то главное значение
аргумента равно

,
т.е.

Замечание.
При сложении и вычитании комплексных
чисел, как правило, целесообразнее
использовать алгебраическую форму этих
чисел. При умножении, возведении в
степень и извлечении корня более
рациональным может оказаться
тригонометрическая или показательная
форма.

Извлечение корня целой положительной степени из комплексного числа

Извлечь корень
целой положительной степени

из числа

значит найти такое число

,

-ая
степень которого равна

Пусть

.
Тогда

и

,
откуда

,

,
откуда

,
(10)

т. е.

,

(10) — формула для
извлечения корня целой положительной
степени

из комплексного числа

Пример 19
Представить следующие выражения в
алгебраической форме: а)

;
б)

.

Решение.
а)

,

,
откуда

и

.

б)

При

при

.●

Пример 20.
Решить уравнение

и изобразить корни этого уравнения на
комплексной плоскости.

Решение.

Подставляя
последовательно

,

,

и

,
получим четыре
различных корня исходного уравнения:

,

,

(рис. 15).●

Рис. 15

ПОНЯТИЕ О ФУНКЦИИ
КОМПЛЕКСНОго
ПЕРЕМЕННОго.

Понятие функции
комплексного переменного вводится по
аналогии с понятием функции действительной
переменной.

Определение.
Величина

называется функцией
комплексного переменного
в области

,
если задан закон, по которому каждому
значению

,
ставится в соответствие одно или
несколько значений

Это соответствие
обозначается в виде

.

Определение.
Переменную

называют независимой
переменной
или аргументом,
а

— зависимой
переменной
или функцией.

Пусть

.

Тогда
из

имеем

и

.

Определение.
Если каждому значению

поставлено
в соответствие одно и только одно
значение

,
то функцию

называют однозначной,
а если несколько значений – то
многозначной.

Определение.
Множество значений

,
где

,
называется областью
значений функции

и обозначается это множество через

.

Геометрически
можно рассматривать

,
заданную на

,
как отображение области

плоскости

(рис. 16) в некоторую область

плоскости

.

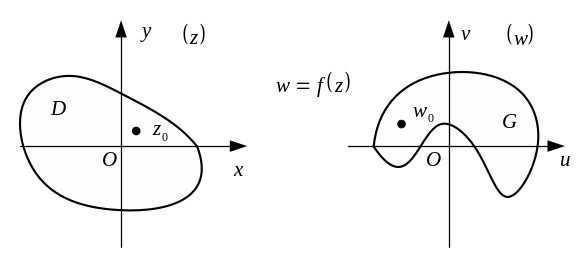
Рис.
16

Определение.
Если

,
то точка

называется образом
точки

при отображении

,
а точка

называется
прообразом
точки

З
амечание.
Иногда удобно совмещать плоскости

.
Тогда функция

«перемещает» точку

в точку

(рис. 17).

Рис.
17
Например,
при отображении

образом точки

является точка

,
т. е

функция

«перемещает» точку

в точку

.
Очевидно,

.

Пример 21
Найти образ точки

,
если отображение задано формулой

.

Решение.

.●

Пример 22.
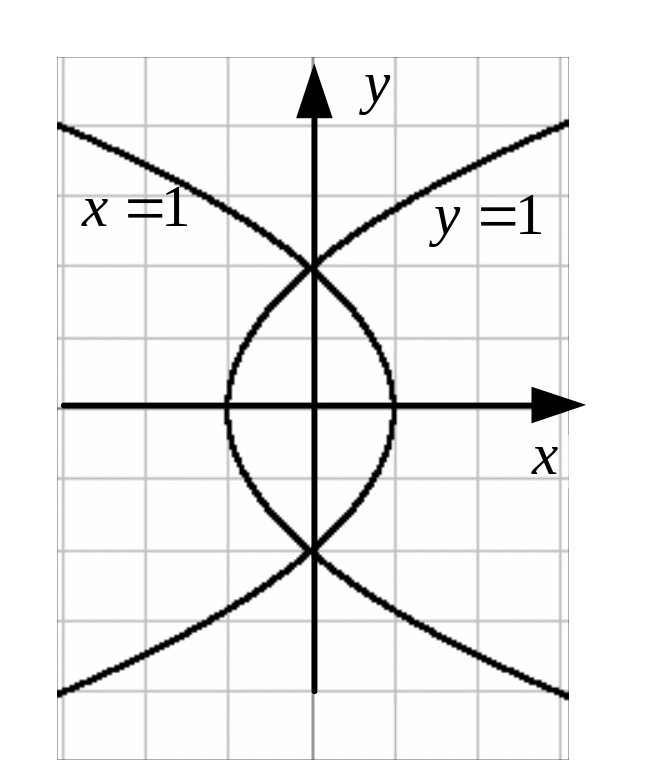
Найти уравнения линий в плоскости

,
на которые с помощью функции

отображаются прямые

и

.

Решение.

,
,
откуда

,
. (11)
Подставляя

в уравнения (11), получим

,
,
откуда

.
Это , уравнение

параболы, симметричной
относительно оси

.

Подставляя

в уравнения (11), получим

,

,
т.е. еще одну параболу

(рис. 18).●

Рис. 18
Пример 23.
Найти образ окружности

при отображении

Решение 1.
Так как

,
то

,
т. е. образом окружности

при указанном отображении является
окружность

.

Решение
2.

,
откуда

Так как

,
то

,

,

и

,
т.е. образом окружности

при отображении

является окружность

.●

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.

Деление в алгебраической форме
Деление в геометрической форме

Деление в алгебраической форме

Результатом деления (т.е. частное) двух комплексных чисел x = a₁ + b₁i и y = a₂ + b₂i также является комплексное число z:

Порядок действий следующий:

Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что i² = -1.

Примечание: Для (a + bi) комплексно сопряженным будет число (a – bi), т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный.
В результате выполнения умножения в знаменателе получается обычное действительное число.
(a₂ + b₂i)(a₂ – b₂i) = a₂ ⋅ a₂ – a₂ ⋅ b₂i + b₂i ⋅ a₂ – b₂i ⋅ b₂i = a₂² – b₂² ⋅ i² = a₂² + b₂².
Теперь выполним аналогичное действие в числителе:
(a₁ + b₁i)(a₂ – b₂i) = a₁ ⋅ a₂ – a₁ ⋅ b₂i + b₁i ⋅ a₂ – b₁i ⋅ b₂i = a₁a₂ – b₁b₂i² – a₁b₂i + b₁a₂i = (a₁a₂ + b₁b₂) + (a₂b₁ – a₁b₂) ⋅ i.
Делим полученный числитель на знаменатель:

Пример 1:
Разделим комплексное число (3 – i) на (-5 + 2i).

Решение:
Руководствуемся планом действий, описанным выше, и получаем:

Деление в геометрической форме

Если комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ₁ + i ⋅ sin φ₁) и y = |y| ⋅ (cos φ₂ + i ⋅ sin φ₂), то разделить их можно по формуле ниже:

Пример 2
Найдем частное комплексных чисел: x = 4 ⋅ (cos 60° + i ⋅ sin 60°) и y = 2 ⋅ (cos 25° + i ⋅ sin 25°).

Решение:
|x| : |y| = 4 : 2 = 2
φ₁ – φ₂ = 60° – 25° = 35°
x : y = 2 ⋅ (cos 35° + i ⋅ sin 35°)

Источник

(схема
43)

Комплексным числом называется выражение вида z=x+iy, (7.1)

где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для
мнимой единицы

i²=–1. (7.2)

Если x=0, то число 0+iy=iy
называется чисто мнимым; если y=0, то число x+i∙0=x
отождествляется с действительным числом x, а это означает, что множество R всех действительных чисел является подмножеством
множества C всех
комплексных чисел, то есть .

Число x называется действительной частью комплексного
числа z и обозначается
x=Re z, а y – мнимой частью комплексного числа z и
обозначается y=Im z.

Два комплексных
числа z₁=x₁+iy₁ и z₂=x₂+iy₂
называются равными (z₁=z₂) тогда, когда равны их действительные и мнимые части: x₁=x₂, y₁=y₂. В частности, комплексное число z=x+iy равно
нулю, когда x=y=0.

Понятия «больше» и «меньше» для комплексных чисел не
вводятся.

Числа z=x+iy и называются комплексно сопряженными.

Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости x0y такой,
что x=Re z, y=Im z.
Верно и обратное: каждую точку M(x;y) координатной
плоскости можно рассматривать как образ комплексного числа z=x+iy (рис. 7.1).

Плоскость, на которой изображаются комплексные числа, называется комплексной
плоскостью. Ось абсцисс называется действительной осью, так как на ней
лежат действительные числа z=x+0∙y=x. Ось ординат – мнимой осью, на ней лежат чисто мнимые комплексные числа z=0+iy.

Комплексное
число z=x+iy можно задавать с помощью радиус-вектора . Длина вектора , изображающего комплексное число z, называется модулем этого числа и обозначается |z| или r. Величина
угла между положительным направлением действительной оси и вектором называется
аргументом комплексного
числа, обозначается Arg z или φ.

Для комплексного числа z=0 аргумент не определен. Аргумент комплексного числа – величина
многозначная и определяется с точностью до слагаемого 2πk (k=0;–1;1;–2;2…): , где arg z – главное значение аргумента,
заключенное в промежутке (–π;π).
Иногда в качестве главного значения аргумента берут величину, принадлежащую
промежутку [0;2π).

Алгебраической
формой комплексного числа называется запись числа z в виде z=x+iy.

Модуль r и
аргумент φ можно рассматривать как
полярные координаты вектора , изображающего комплексное число z=x+iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем

. Следовательно, комплексное число
z=x+iy можно
записать в виде или

. (7.3)

Равенство
(7.3) есть тригонометрическая форма
комплексного числа. Модуль r=|z| однозначно
определяется по формуле

. (7.4)

Аргумент определяется из формул:

. (7.5)

При переходе от
алгебраической формы комплексного числа к тригонометрической достаточно
определить главное значение аргумента комплексного числа z, то есть
считать φ=arg z. Знаки полученных значений cos φ и sin φ по
формулам (7.5), дают возможность определить, какой координатной четверти
принадлежит угол φ.

Используя формулу
Эйлера

, (7.6)

комплексное число можно записать в так
называемой показательной (или
экспоненциальной) форме

z=reⁱ^φ, (7.7)

где r=|z| — модуль комплексного числа, а угол (k=0;–1;1;–2;2…).

Функция eⁱ^φ – периодическая с основным периодом 2π, поэтому для записи комплексного числа в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ=arg z.

Пример 7.1. Записать
комплексные числа в
тригонометрической и показательной формах.

Решение. Для z₁ имеем . Поэтому .

Для действительного числа . Поэтому

На множестве комплексных чисел определен ряд операций.

1.
Суммой двух
комплексных чисел z₁=x₁+iy₁ и z₂=x₂+iy₂
называется комплексное число, определяемое равенством

. (7.8)

Из (7.8) следует, что геометрически комплексные числа складываются как
векторы, причем сумма комплексных чисел интерпретируется как диагональ
параллелограмма, построенного на векторах, представляющих слагаемые (рис. 7.2).

2.
Вычитание
комплексных чисел определяется
как действие, обратное сложению. Разностью двух комплексных чисел z₁ и z₂
называется такое комплексное число z, которое, будучи сложенным с z₂, дает число z₁, то есть
z= z₁– z₂, если z+z₂=z₁. Если z₁=x₁+iy₁, z₂=x₂+iy₂, то из
этого определения получаем:

(7.9)

Из равенства (7.9) следует, что геометрически
комплексные числа вычитаются как векторы. При этом число z= z₁– z₂
изображается вектором, соединяющим концы векторов , и исходящим из конца
вычитаемого в конец уменьшаемого (см. рис. 7.2).
Таким образом, модуль разности двух комплексных чисел равен расстоянию d между
точками, изображающими эти числа на плоскости:

. (7.10)

3.
Произведением комплексных чисел z₁=x₁+iy₁ и z₂=x₂+iy₂ называется
комплексное число, определяемое равенством

. (7.11)

Из (7.11) следует важнейшее соотношение i²= –1.
Действительно,

Найдем произведение комплексных чисел и . Производя все необходимые выкладки согласно формуле (7.11),
получим формулу произведения комплексных чисел, заданных в тригонометрической форме:

. (7.12)

Видно, что при умножении комплексных чисел в
тригонометрической форме их модули перемножаются, а аргументы складываются. Это
правило распространяется на любое конечное число множителей. Нетрудно видеть,
что если есть n множителей и все они одинаковые, то частным случаем
равенства (7.12) является формула возведения комплексного числа в
натуральную
степень:

. (7.13)

(7.13)
называется первой формулой Муавра.

Произведение двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

. (7.14)

4.
Частным двух
комплексных чисел z₁ и называется комплексное
число z, которое, будучи умноженным на z₂, дает число z₁, то есть , если .

Пусть , тогда с использованием этого определения получаем:

. (7.15)

На практике при нахождении частного двух комплексных чисел
удобно умножить числитель и знаменатель дроби на число, сопряженное
знаменателю, с дальнейшим применением равенства i²= –1 и формулы разности квадратов.

Деление комплексных чисел осуществляется также и в
тригонометрической форме, при этом имеет место формула:

. (7.16)

Видно, что при делении
комплексных чисел их модули делятся, а
аргументы вычитаются соответственно.

Частное двух комплексных чисел в показательной
(экспоненциальной) форме имеет вид:

. (7.17)

Пример 7.2. Найти
сумму, разность, произведение и частное комплексных чисел .

Решение. По
формуле (7.8) сумма заданных чисел равна .

Согласно формуле (7.9) разность заданных чисел равна .

Пользуясь формулой (7.11), вычислим их произведение

На основании формулы (7.14) вычислим их частное

Пример 7.3. Найти
произведение и частное комплексных чисел , представив их в тригонометрической и показательной форме.

Решение.
Используя (7.4) и (7.5), получаем:

. Следовательно, на основе формул
(7.3) и (7.7) число z₁ имеет
тригонометрическую и показательную форму

Аналогично, для z₂ можно
записать:

. Отсюда .

По формулам (7.12) и (7.16) получим в
тригонометрической форме:

Пользуясь формулами (7.14) и (7.17), получим в
показательной форме:

5.
Извлечение
корня n-ой
степени – операция, обратная возведению

в натуральную степень, определенному ранее формулой (7.13).

Корнем n-ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωⁿ=z, то есть , если ωⁿ=z.

Пусть , тогда по данному
определению и формуле (7.13) Муавра можно записать: . Сравнивания части этого равенства, получим: . Отсюда (корень
арифметический). Окончательно получаем:

. (7.18)

(7.18) называется второй формулой Муавра.

Видно, что для
любого корень n-ой степени
из комплексного числа z имеет равно n различных значений.

Пример 7.4. Найти все корни уравнения z⁴+16=0.

Решение.
Запишем уравнение в виде z⁴=–16+0∙i. Отсюда по
формуле (7.18) получим:

Рассмотрим различные значения k=0;1;2;3.

Корни z₁ и z₄, а также
z₂ и z₃ являются
комплексно сопряженными. Таким образом, корнями заданного уравнения z⁴+16=0
являются комплексные числа

Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел.

Теорема 7.1 (основная теорема алгебры). Для всякого
многочлена с комплексными коэффициентами

степени n>0
существует точка , в которой P(z₀)=0

Приведем еще
одну теорему, имеющую место над множеством комплексных чисел.

Теорема 7.2. Если
многочлен P_n(x) с действительными коэффициентами имеет комплексный
корень a+ib, то он
имеет и сопряженный корень a–ib

В разложение
многочлена комплексные корни
входят сопряженными парами. Пусть корни многочлена x₁=a+ib и x₂=a–ib. Перемножив линейные множители
разложения , получим трехчлен второй степени с действительными
коэффициентами x²+px+q и
отрицательным дискриминантом. Действительно,

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.

Вопросы
для самопроверки

Источник

Найти сумму, разность, произведение и частное комплексных чисел

Пусть даны два комплексных числа в алгебраической форме $z_1 = a + bi, z_2 = c + di$, тригонометрической форме $z_1 = r_1 (cos varphi_1 + isin varphi_1), z_2 = r_2(cos varphi_2 + isin varphi_2)$ и показательной форме $z_1 = r_1 e^{varphi_1 i} , z_2 = r_2 e^{varphi_2 i}$.

Формула суммы и разности

В алгебраической форме $$z_1 + z_2 = (a+bi) + (c+di) = (a + c) + (b + d)i, $$ $$z_1 — z_2 = (a+bi) — (c+di) = (a-c) + (b — d)i, $$в тригонометрической и показательной форме тоже можно выполнять сложение и вычитание, но удобнее это делать в алгебраической.

Формула произведения

В алгебраической форме $$z_1 cdot z_2 = (a+bi) cdot (c+di) = (ac — bd) + i(ad + bc),$$ в тригонометрической форме $$z_1 cdot z_2 = r_1 r_2 (cos (varphi_1 + varphi_2) + isin (varphi_1 + varphi_2)),$$в показательной форме $$z_1 cdot z_2 = r_1 r_2 e^{(varphi_1+varphi_2)i}.$$

Формула деления

В алгебраической форме $$frac{z_1}{z_2} =frac{z_1 overline{z_2}}{z_2 overline{z_2}} = frac{ac+bd}{c^2+d^2} + frac{bc-ad}{c^2+d^2}i, $$в тригонометрической форме $$frac{z_1}{z_2} = frac{r_1}{r_2} (cos(varphi_1 — varphi_2)+isin(varphi_1-varphi_2)),$$в показательной форме $$frac{z_1}{z_2} = frac{r_1}{r_2}e^{(varphi_1 — varphi_2)i}.$$

Введите первое комплексное число

Введите второе комплексное число

Пример 1

Найти сумму, разность, произведение, частное комплексных чисел $$z_1 = 1+2i, z_2 = -2+i.$$

Решение

Сначала находим сумму. Для этого раскрываем скобки и проводим вычисления с подобными $$z_1 + z_2 = (1+2i) + (-2+i) = 1+2i — 2 + i = (1-2) + (2i+i) = -1 + 3i.$$

Тоже самое делаем для того, чтобы найти разность. Раскрываем скобки и вычисляем $$z_1 — z_2 = (1+2i) — (-2+i) = 1+2i + 2 — i = 3 + i.$$

Теперь найдем произведение чисел. Раскрываем скобки попарно перемножая слагаемые в скобках. Но не забываем, что $i = sqrt{-1}$, а это значит, что $i^2 = -1$, получаем $$z_1 cdot z_2 = (1+2i)cdot (-2+i) = -2 + i — 4i + 2i^2 = $$ $$ = -2 — 3i — 2 = -4-3i.$$

Выполним деление комплексных чисел. Здесь необходимо числитель и знаменатель домножить на комплексно-сопряженное число к знаменателю, чтобы избавиться от дроби $$frac{z_1}{z_2} = frac{1+2i}{-2+i} = frac{(1+2i)(-2-i)}{(-2+i)(-2-i)} = $$ В числителе и знаменателе раскрываем скобки, то есть выполняем умножение комплексных чисел по соответствующей формуле. И не забываем про то, что $i^2 = -1$ $$ = frac{-2-i-4i-2i^2}{4+2i-2i-i^2} = frac{-2-5i+2}{4+1} = frac{-5i}{5} = -i.$$

Ответ

$$z_1 + z_2 = -1+3i, z_1 — z_2 = 3+i, z_1 cdot z_2 = -4-3i, frac{z_1}{z_2} = -i$$

Пример 2

Найти произведение и частное комплексных чисел $z_1 = 2(cos frac{pi}{3} + isin frac{pi}{3})$ и $z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6})$

Решение

Начнем с умножения двух чисел. Вычисляем произведение модулей и складываем аргументы синуса и косинуса $$z_1 cdot z_2 = 2(cos frac{pi}{3} + isin frac{pi}{3}) cdot 4(cos frac{pi}{6} + isin frac{pi}{6}) = $$ $$ = 8 (cos (frac{pi}{3} + frac{pi}{6}) + isin (frac{pi}{3}+frac{pi}{6})) = 8(cosfrac{pi}{2} + isin frac{pi}{2}).$$

Деление выполняется наоборот. Ищем частное модулей и разность аргументов $$frac{z_1}{z_2} = frac{2}{4} (cos (frac{pi}{3} — frac{pi}{6}) +isin (frac{pi}{3}-frac{pi}{6}) = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6}).$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$z_1 cdot z_2 = 8(cosfrac{pi}{2} + isin frac{pi}{2}), frac{z_1}{z_2} = frac{1}{2} (cos frac{pi}{6} + isin frac{pi}{6})$$

Пример 3

Найти произведение и частное комплексных чисел $ z_1 = 6e^{frac{pi}{2}i} $ и $ z_2 = 2e^{frac{pi}{4}i} $

Решение

Для умножения двух комплексных чисел необходимо перемножить их аргументы и сложить показатели степеней $$z_1 cdot z_2 = 6e^{frac{pi}{2}i} cdot 2e^{frac{pi}{4}i} = 12e^{(frac{pi}{2}+frac{pi}{4})i} = 12e^{frac{3pi}{4}i}.$$

Для деления нужно найти частное аргументов двух комплексных чисел и вычислить разницу показателей степеней $$frac{z_1}{z_2} = frac{6e^{frac{pi}{2}i}} {2e^{frac{pi}{4}i}} = frac{6}{2} e^{(frac{pi}{2}-frac{pi}{4})i} = 3e^{frac{pi}{4}i}.$$

Ответ

$$z_1 cdot z_2 = 12e^{frac{3pi}{4}i}, frac{z_1}{z_2} = 3e^{frac{pi}{4}i}$$

Источник

Деление комплексных чисел — основные правила

Определение 1

Частным двух комплексных чисел (z_{1}=a_{1}+b_{1} i) и (z_{2}=a_{2}+b_{2} )i называют число z, заданное соотношением: (z=frac{z_{1}}{z_{2}}=frac{a_{1} a_{2}+b_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}}+frac{a_{2} b_{1}-a_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}} i)

Общий алгоритм для деления комплексных чисел на практике:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

умножение делимого и делителя на число, комплексно сопряженное делителю, что преобразует делитель в действительное число;
в числителе умножают пару комплексных чисел;
полученную дробь почленно делят.

В каких формах это можно делать

Комплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу.

Формула деления в алгебраической форме

Когда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе:

(frac{z_1}{z_2} = frac{a_1 + b_1 i}{a_2 + b_2 i} = frac{(a_1+b_1 i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} = frac{a_1 cdot a_2 + b_1 cdot b_2}{a_2 ^2 + b_2 ^2} + ifrac{a_2 cdot b_1 — a_1 cdot b_2}{a_2 ^2 + b_2 ^2})

Формула деления в тригонометрической форме

Деление в тригонометрической форме подразумевает деление модулей комплексных чисел. После выполнения данной операции определяют разность аргументов:

(frac{z_1}{z_2} = frac{r_1}{r_2} (cos (varphi_1 — varphi_2) + isin (varphi_1 — varphi_2)))

Формула деления в показательной форме

Показательная форма деления комплексных чисел в тригонометрии предполагает деление модулей и вычисление разности аргументов в экспоненте:

(frac{z_1}{z_2} = frac{r_1}{r_2} e^{(varphi_1 — varphi_2)i})

Примеры решения задач

Задача 1

Задача

Необходимо найти частное пары комплексных чисел:

(z_1 = 3+i) и (z_2 = 2-3i)

Решение:

Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.

(frac{z_1}{z_2} = frac{3+i}{2-3i} =)

Сопряженное комплексное число к знаменателю:

(overline{z_2} = 2+3i)

Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:

(= frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =)

Далее следует привести подобные слагаемые и записать вывод с ответом:

(= frac{3 + 11i}{13} = frac{3}{13} + frac{11}{13}i)

Ответ: (frac{z_1}{z_2} = frac{3}{13} + frac{11}{13}i)

Задача 2

Задача

Требуется выполнить деление комплексных чисел:

(z_1 = 2(cos frac{pi}{3} + isin frac{pi}{6}))

(z_2 = 4(cos frac{pi}{6} + isin frac{pi}{6}))

Решение:

Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:

Деление модулей:

(frac{r_1}{r_2} = frac{2}{4} = frac{1}{2})

Разность аргументов:

(varphi_1 — varphi_2 = frac{pi}{3} — frac{pi}{6} = frac{pi}{6})

Следующим шагом является деление чисел:

(frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Ответ: (frac{z_1}{z_2} = frac{1}{6} (cos frac{pi}{6} + isin frac{pi}{6} ))

Задача 3

Задача

Нужно найти частное комплексных чисел:

(z_1 = 3e^{frac{pi}{2}i})

(z_2 = 4e^{frac{pi}{4}i})

Решение: Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:

(frac{r_1}{r_2} = frac{3}{4})

(varphi_1 — varphi_2 = frac{pi}{2} — frac{pi}{4} = frac{pi}{4})

При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:

(frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Ответ: (frac{z_1}{z_2} = frac{3}{4} e^{frac{pi}{4}i})

Задача 4

Задача

Определить частное:

(frac{-2+i}{1-i})

Решение:

В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:

(1-i)

Данным числом является:

(1+i)

Таким образом:

(frac{-2+i}{1-i}=frac{-2+i}{1-i} cdot frac{1+i}{1+i}=frac{(-2+i)(1+i)}{(1-i)(1+i)})

Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:

(i^{2}=-1)

(frac{-2+i}{1-i}=frac{(-2+i)(1+i)}{(1-i)(1+i)}=frac{-2-2 i+i-1}{1^{2}-i^{2}}=)

(=frac{-3-i}{1-(-1)}=frac{-3-i}{2}=-frac{3}{2}-frac{i}{2})

Ответ:( frac{-2+i}{1-i}=-frac{3}{2}-frac{i}{2})

Задача 5

Задача

Необходимо найти частное:

(frac{z_{1}}{z_{2}})

При условии, что:

(z_{1}=2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right))

(z_{2}=cos frac{pi}{4}+i sin frac{pi}{4})

Решение:

Искомое частное:

(frac{z_{1}}{z_{2}}=frac{2 cdotleft(cos frac{3 pi}{4}+i sin frac{3 pi}{4}right)}{cos frac{pi}{4}+i sin frac{pi}{4}}=)

(=frac{2}{1} cdotleft[cos left(frac{3 pi}{4}-frac{pi}{4}right)+i sin left(frac{3 pi}{4}-frac{pi}{4}right)right]=)

(=2 cdotleft[cos frac{pi}{2}+i sin frac{pi}{2}right]=2 cdot(0+i)=2 i)

Ответ: (frac{z_{1}}{z_{2}}=2 cdotleft(cos frac{pi}{2}+i sin frac{pi}{2}right)=2 i)

Задача 6

Задача

Необходимо разделить два комплексных числа:

(z_{1}=-1+3i)

(z_{2}=1+2i)

Решение:

С помощью соответствующей формулы можно записать уравнение:

(z_{1} div z_{2} = frac{-1+3i}{1+2i} = frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = frac{-1 cdot 1 + 3 cdot 2}{1^{2}+2^{2}} + i frac{3 cdot 1 + (-1) cdot (-2)}{1^{2}+2^{2}} =)

(= frac{5}{5} + i frac{5}{5}=1+i)

Ответ: ( z_{1} div z_{2} = 1+i)

Задача 7

Задача

Необходимо вычислить частное комплексных чисел:

(z_{1}=sqrt{2} left( cos frac{pi}{2} + i sin frac{pi}{2} right))

(z_{2}=sqrt{2} left( cos frac{pi}{4} + i sin frac{pi}{4} right))

Решение:

Используя соответствующую формулу, запишем:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} (cos ( varphi _{1} — varphi _{2}) + i sin ( varphi _{1} — varphi _{2})) = frac{sqrt{2}}{sqrt{2}} left( cos left( frac{pi}{2}-frac{pi}{4} right) + i sin left( frac{pi}{2}-frac{pi}{4} right) right) =)

(= 1 cdot left( cos frac{pi}{4} + i sin frac{pi}{4} right) = cos frac{pi}{4} + i sin frac{pi}{4})

Ответ:( z_{1} div z_{2} = cos frac{pi}{4} + i sin frac{pi}{4})

Задача 8

Задача

Требуется разделить два комплексных числа:

(z_{1} = sqrt{2} e^{-frac{pi}{2}i})

(z_{2} = 2 e^{-frac{pi}{4}i})

Решение:

Используя соответствующую формулу деления комплексных чисел, можно решить уравнение:

(z_{1} div z_{2} = frac{r_{1}}{r_{2}} cdot e^{i ( varphi _{1} — varphi _{2})} = frac{sqrt{2}}{2} cdot e^{i left( -frac{pi}{2} +frac{pi}{4} right) } = frac{sqrt{2}}{2} cdot e^{-frac{pi}{4}i})

Ответ: (z_{1} div z_{2} = frac{sqrt{2}}{2} cdot e^{-frac{pi}{4}i})

Источник