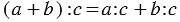Математика
6 класс
Урок № 42
Деление дробей
Перечень рассматриваемых вопросов:
- деление рациональных чисел, правила знаков при делении.
Тезаурус
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей делимого и делителя.
Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлом уроке мы изучали правила умножения дробей.
Сегодня рассмотрим правила деления.
Аналогично умножению, дроби с любыми знаками делят по тем же правилам, что и положительные дроби.
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Найдём частное от деления двух дробей.
Запишем равенство, которое можно получить на основании правила деления.
Доказательство
Чтобы разделить дробь на целое, не равное нулю число, можно её знаменатель умножить на это число.
Найдём частное
Знак «–» перед дробью, можно записывать и в знаменателе, и в числители дроби, то есть верны равенства:
Используя свойство взаимно обратных дробей, что их произведение равно 1, можем сформулировать следующее утверждение:
Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.
Найдём частное
Правила знаков, при делении дробей
Правило деления дробей с одинаковыми знаками
Частным двух дробей с одинаковыми знаками является положительная дробь, равная частному модулей делимого и делителя.
Выполним деление
Правило деления дробей с разными знаками
Частное от деления дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.
Выполним деление
Из правил деления дробей с любыми знаками следует, что их можно делить по тем же правилам, что и целые числа. То есть мы можем сначала определять знак результата, а потом выполнять действия с модулями.
Выполним деление
Дополнительный материал
Решение задачи
Решение
Найдём, сколько автомобиль проехал за второй час. Известно, что в 2 раза меньше, чем за первый, значит, путь за первый час разделим на 2.
Найдём общую часть пути за два часа.
Для этого сложим части пути за первый и за второй час.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие действия изображены?
Варианты ответов:
деление дробей с одинаковыми знаками
деление дробей с разными знаками
деление дроби на целое число
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Частное двух дробей есть дробь, … которой равен … числителя первой дроби и … второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
Варианты слов для вставки:
числитель
произведению
частному
сумме
разности
знаменателя
Для ответа на вопрос задания, обратимся к теоретическому материалу урока.
Правильный ответ:
Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.
В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь разделить на число или другую дробь, и как найти частное от деления смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
-
Деление дроби
- На число
- На другую дробь
- Деление смешанных дробей
- Примеры задач
Деление дроби
На число
Результатом деления обыкновенной дроби на число n является дробь, знаменатель которой равняется произведению знаменателя исходной дроби и этого числа n. Числитель при этом остается тем же.
Примечание: после выполнения деления не забываем проверить, можно ли сократить новую дробь.
На другую дробь
Чтобы разделить одну дробь на другую, переворачиваем дробь-делитель (меняем местами числитель и знаменатель) и умножаем ее на дробь-делимое, которое оставляем без изменений.
a/b
:
c/d
=
a/b
⋅
d/c
=
a ⋅ d/b ⋅ c
Деление смешанных дробей
Чтобы найти частное от деления смешанных дробей, для начала их нужно представить в виде неправильных дробей, и только после этого выполнить деление.
X
a/b
: Y
c/d
=
X ⋅ b + a/b
:
Y ⋅ d + c/d
=
X ⋅ b + a/b
⋅
d/Y ⋅ d + c
=
(X ⋅ b + a) ⋅ d/(Y ⋅ d + c) ⋅ b
Примеры задач
Задание 1
Разделите дробь
5/6
на число 5.
Решение
5/6
: 5 =
5/6⋅5
=
5/30
=
1/6
Задание 2
Разделите дробь
4/15
на
2/9
.
Решение
4/15
:
2/9
=
4/15
⋅
9/2
=
4⋅9/15⋅2
=
36/30
=
6/5
= 1
1/5
Задание 3
Найдите частное от деления дроби 6
1/4
на дробь 4
2/3
.
Решение
Т.к. даны смешанные дроби, сначала запишем их в виде неправильных, потом выполним требуемое действие.
6
1/4
: 4
2/3
=
6⋅4+1/4
:
4⋅3+2/3
=
25/4
:
14/3
=
25/4
⋅
3/14
=
25⋅3/4⋅14
=
75/56
=1
19/56
Содержание
- Деление и дроби
- Дробные выражения
- —>Сайт учителя математики А.В.Капитановой —>
- Умножение дроби на натуральное число
- Пример: Найти произведение дроби и натурального числа:
- Пример: Найти произведение двух смешанных чисел:
- Пример: Найти частное от деления дроби на натуральное число:
- Пример: Найти частное от деления дробей:
- Пример: Найти частное от деления смешанных чисел:
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
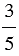
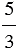
В результате деления двух натуральных чисел может получится натуральное число или дробное число.
Пример:
20 : 4 = 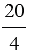
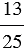
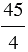
Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем.
Пример:
а) 1 = 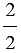
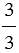
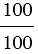
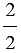
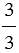
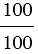
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
б) 7 = 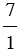
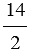
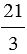
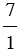
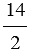
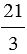
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
Частное от деления одного выражения на другое можно записать с помощью черты дроби. Например, выражение (3,5 — 1,1) : (7,3 + 2,7) можно записать в виде 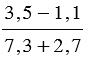
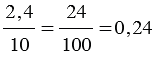
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
К дробным выражениям относятся:
Числитель дробного выражения — выражение, стоящее над чертой.
Знаменатель дробного выражения — выражение, стоящее под чертой.
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
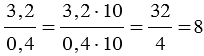
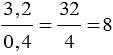
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
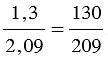
Поделись с друзьями в социальных сетях:
Источник
—>Сайт учителя математики А.В.Капитановой —>
Умножение дроби на натуральное число
Пример: Найти произведение дроби и натурального числа:
Умножение обыкновенных дробей
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Умножение смешанных чисел
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример: Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример: Найти произведение смешанного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 5 · 9 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 · 5 | 7 | 7 | 7 |
Деление дроби на натуральное число
Пример: Найти частное от деления дроби на натуральное число:
Определение: Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель.
Деление натурального числа на дробь
Пример: Найти частное от деления натурального числа на дробь:
| 2: | 4 | = | 2· | 5 | = | 2 · 5 | = | 2 · 5 | = | 5 | = | 2 · 2 + 1 | = 2 | 1 |
| 5 | 4 | 4 | 2 · 2 | 2 | 2 | 2 |
Деление обыкновенных дробей
Пример: Найти частное от деления дробей:
| 3 | : | 4 | = | 3 | · | 5 | = | 3 · 5 | = | 15 |
| 7 | 5 | 7 | 4 | 7 · 4 | 28 |
Деление смешанных чисел
- преобразовать смешанные дроби в неправильные;
- умножить первую дробь на дробь, обратную второй;
- сократить полученную дробь;
- если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Пример: Найти частное от деления смешанных чисел:
| 1 | 1 | : | 2 | 2 | = | 1 · 2 + 1 | : | 2 · 3 + 2 | = | 3 | : | 8 | = | 3 | · | 3 | = | 3 · 3 | = | 9 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 | 8 | 2 · 8 | 16 |
Пример: Найти частное от деления смешанного числа на дробь:
Источник
Обновлено: 24.05.2023
Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.
Деление дроби на дробь.
Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.
Выполните деление обыкновенных дробей .
Деление дроби на число.
Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.
Выполните деления дроби на натуральное число (frac div 3).
Как мы уже знаем, что любое число можно представить в виде дроби (3 = frac ).
Деление числа на дробь.
Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.
Выполните деление числа на дробь.
Деление смешанных дробей.
Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.
Выполните деление смешанных дробей.
Деление числа на число.
Чтобы поделить простые числа, нужно представить их в виде дроби и выполнить деление по правилам деления дроби на дробь.
Примечание к теме деление дробей:
На нуль делить нельзя.
Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.
Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.
Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) (frac div frac) б) (2frac div 1frac)
( frac) – делитель, ( frac) – обратная дробь делителя.
( frac) – делитель, ( frac) – обратная дробь делителя.
Пример №2:
Вычислите деление: а) (5 div 1frac) б) (9frac div 
Научившись умножать обыкновенные дроби, несложно научиться их делить. Как обычно, рассмотрим какие случаи могут нам встретиться при вычислении примеров на деление дробей.
Деление дроби на дробь
Чтобы разделить одну обыкновенную дробь на другую, отличную от нуля, нужно:
- числитель первой дроби умножить на знаменатель второй дроби и записать произведение в числитель новой дроби;
- знаменатель первой дроби умножить на числитель второй дроби и записать произведение в знаменатель новой дроби.
Другими словами, деление дробей сводится к умножению. Поэтому правила деления дробей можно записать следующим образом.
Чтобы разделить одну дробь на другую, надо делимое (первую дробь) умножить на обратную дробь делителю.
Как дробь разделить на число
Чтобы разделить дробь на натуральное число, можно использовать следующий способ.
Мы представляем натуральное число в виде неправильной дроби с числителем, равным самому числу, а знаменатель равным единице.
Затем призводим деление по правилу деления дроби на дробь.
Деление смешанных чисел
При делении смешанных чисел надо представить числа в виде неправильных дробей, а потом разделить их друг на друга по правилу деления дроби на дроби.
В случае деления целого числа на обыкновенную дробь целое число можно умножить на дробь, обратную делителю, или сначала представить целое число в виде неправильной дроби, а затем выполнить деление обыкновенных дробей:
8 : 4 5 = 8 ⋅ 5 4 = 8 2 ⋅ 5 4 1 = 2 ⋅ 5 1 = 10 1 = 10 ; 8 : 4 5 = 8 1 : 4 5 = 8 1 ⋅ 5 4 = 8 2 ⋅ 5 4 1 = 2 ⋅ 5 1 = 10 1 = 10 .
Чтобы найти частное смешанных чисел, смешанные числа представляют в виде неправильных дробей и выполняют деление по правилу деления обыкновенных дробей:
3 2 5 : 1 5 = 3 ⋅ 5 + 2 5 : 1 5 = 17 5 : 1 5 = 17 5 ⋅ 5 1 = 17 ⋅ 5 1 5 1 ⋅ 1 = 17 ⋅ 1 1 ⋅ 1 = 17 1 = 17 ; 4 1 2 : 6 3 4 = 9 2 : 27 4 = 9 2 ⋅ 4 27 = 9 1 ⋅ 4 2 2 1 ⋅ 27 3 = 1 ⋅ 2 1 ⋅ 3 = 2 3 .
Дроби — тема в математике, которую точно нельзя пропустить. Ведь мы сталкиваемся с ними почти в каждой сфере жизни: музыка, медицина, строительство. В этой статье обсудим деление.
О чем эта статья:
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b.
Существует два формата записи:
обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — .
Основные свойства дроби
1. Дробь не имеет значения, при условии, если знаменатель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Две дроби a/b и c/d называются равными, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление дробных чисел
Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.
Свойства деления:
При делении на единицу получится такое же число: a : 1 = a.
На ноль делить нельзя.
При делении нуля на что-либо получится ноль: 0 : a = 0.
При делении числа на само себя получится единица: a : a = 1.
При деления суммы на какое-либо число, можно разделить на него каждое слагаемое и сложить полученные результаты: (a + b) : c = a : c + b : c.
При делении разности на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе: (a — b) : c = a : c — b : c.
При делении произведения двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель: (a * b) : c = (a : c) · b = a * (b : c).
Деление обыкновенных дробей
Как делить дробь на дробь? Выполняем следующую последовательность действий:
числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам не важно, одинаковые знаменатели или нет.
Деление дроби на натуральное число
Для деления дроби на натуральное число нужно:
представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;
произвести деление по предыдущему правилу.
Деление натурального числа на дробь
Чтобы поделить натуральное число на обыкновенную дробь нужно:
делимое записать в виде дроби;
умножить полученную дробь на дробь, обратную делителю, воспользовавшись алгоритмом, который мы уже разобрали выше.
Читайте также:
- Смысл названия рассказа ионыч чехова кратко
- Европейский кодекс поведения юристов кратко
- Действие это кратко и понятно
- Авторитет и псевдоавторитет тренера кратко
- Моральные проблемы пренатальной диагностики кратко
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. ab : cd = ab ⋅ dc = a⋅d b⋅c Найдём частное двух обыкновенных дробей. Пример: 37 : 45 = 37 ⋅ 54 = 3⋅5 7⋅4 = 1528 При необходимости, дробь сокращают. Пример: 49 : 23 = 49 ⋅ 32 = 42 ⋅ 31 93 ⋅ 21 = 2⋅1 3⋅1 = 23 В случае деления целого числа на обыкновенную дробь, целое число можно умножить на дробь обратную делителю, или сначала представить целое число в виде неправильной дроби, а затем выполнить деление обыкновенных дробей. 8: 45 = 8⋅ 54 = 82 ⋅5 41 = 2⋅5 1 = 101 = 10 8: 45 = 81 : 45 = 81 ⋅ 54 = 82 ⋅5 41 = 2⋅5 1 = 101 = 10 Чтобы найти частное смешанных чисел, смешанные числа представляют в виде неправильных дробей и выполняют деление по правилу деления обыкновенных дробей. 3 25 : 15 = 3⋅5+2 5 : 15 = 175 : 15 = 175 ⋅ 51 = 17⋅ 51 51 ⋅1 = 17⋅1 1⋅1 = 171 = 17 4 12 : 6 34 = 92 : 274 = 92 ⋅ 427 = 91 ⋅ 42 21 ⋅ 273 = 1⋅2 1⋅3 = 23