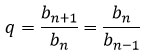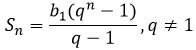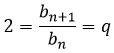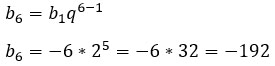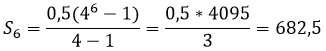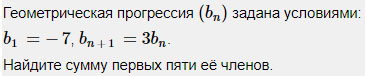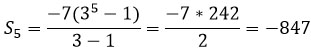Как найти частное геометрической прогрессии - Исправление недочетов и поиск решений вместе с Examum.ru

запиши периодическую дробь (0,(8)) обыкновенной дробью.

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…) Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по формуле:

S=b11−q=0,81−0,1

Осталось выполнить нужные действия с десятичными дробями:

0,81−0,1=0,80,9=89

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Источник

Определение

Геометрическая прогрессия — числовая последовательность, в которой каждый следующий член отличается от предыдущего в определенное количество раз. Частное двух соседних элементов геометрической прогрессии постоянно.

Формула -ого члена геометрической прогрессии

$[b_n=b_1cdot q^{n-1}]$

Пример 1. Найдите знаменатель геометрической прогрессии, если третий элемент геометрической прогрессии равен , а -ый — .

Решение.

Третий элемент прогрессии равен , а шестой элемент прогрессии — $b_{6}=b_1 cdot q^5$ . Сложим данные равенства.

Получим:

$[frac{b_{6}}{b_3}=frac{q^5}{q^2};]$

$[q=sqrt[3]{frac{224}{28}};]$

Ответ: .

Сумма геометрической прогрессии

Запишем сумму элементов геометрической прогрессии:

$[S_n=b_1+b_2+b_3+ldots+b_n=b_1+b_1q+b_1q^2+ldots+b_1q^{n-1}.]$

Прибавим к левой и правой части равенства .

Получим:

$[S_n+b_1q^n=b_1+b_1q+b_1q^2+ldots+b_1q^{n-1}+b_1q^n=b_1+q cdot S_n]$

$S_n=b_1frac{1-q^n}{1-q}$ , если

Если , то

Пример 2. Найдите сумму чисел $frac{1}{2}+frac{1}{4}+frac{1}{8}+frac{1}{16}+frac{1}{32}.$

Решение.

$frac{1}{2}+frac{1}{4}+frac{1}{8}+frac{1}{16}+frac{1}{32}=frac{1}{2}cdot frac{1-{left ( frac{1}{2}right )}^5}{1-frac{1}{2}}=1-frac{1}{32}=frac{31}{32}.$

Ответ: $frac{31}{32}$ .

Бесконечно убывающей геометрической прогрессией называется бесконечная геометрическая прогрессия, знаменатель которой удовлетворяет условию .

При неограниченном возрастании сумма $S_n=b_1frac{1-q^n}{1-q}$ , первых членов бесконечно убывающей геометрической прогрессии стремится к числу $S=frac{b_1}{1-q}$ , которое называется суммой бесконечно убывающей геометрической прогрессии.

Пример 3. Переведите бесконечную периодическую дробь в обыкновенную дробь.

Решение.

$0,(8)=frac{8}{10}+frac{8}{100}+frac{8}{1000}+frac{8}{10000}+ldots=frac{0,8}{1-frac{1}{10}}=frac{0,8}{0,9}=frac{8}{9}$

Ответ: $frac{8}{9}$ .

Характеристическое свойство геометрической прогрессии

$[b_n^2=b_{n-1} cdot b_{n+1}]$

Пример 4. Выписано несколько последовательных членов геометрической прогрессии:

Найдите .

Решение.

, так как в данной геометрической прогрессии .

Ответ: .

Источник

Геометрическая прогрессия

Кусочек теории.

Геометрическая прогрессия — это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.

Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.

Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.

Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:

Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:

Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:

И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!

Помимо этих трех формул пригодится еще формула суммы:

Практика.

Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)

Откинем пока минусы…

Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.

Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.

И 5-ое: 64 : 1,25 = 51,2.

Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое — положительным.

Ответ: 51,2.

Задание 2.

Опять знаки у чисел чередуются, значит число, спрятанное под иксом, будет отрицательным.

Не будем морочить голову формулами, пойдем задом наперед: разделим 4-ое число на 3-ое (найдем знаменатель прогрессии):

96 : 24 = 4 (знаки у чисел мы откинули временно).

Значит, чтобы найти икс надо 24 разделить на знаменатель 4 и взять результат с минусом.

Ответ: -6.

Задание 3.

По данной нам в условии задаче формуле можно сразу понять, что 2 — знаменатель прогрессии. Если это не понятно — вот доказательство:

Здесь схитрить не получится, поэтому используем формулу и находим b₆.

Ответ: -192.

Задание 4.

Каждое следующее число в 4 раза больше предыдущего, значит знаменатель q равен 4.

Зная первый член прогрессии и знаменатель можно найти сумму первых шести членов (n = 6).

Ответ: 682,5.

Задание 5.

Похожее условие уже встречалось в задании 3. Из данной формулы делаем вывод, что знаменатель q = 3.

Находим сумму:

Ответ: -847.

Вот и всё!

С наилучшими пожеланиями, твой персональный препод)

Источник