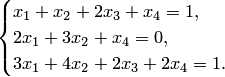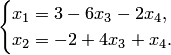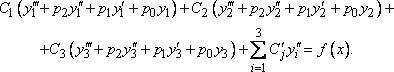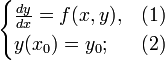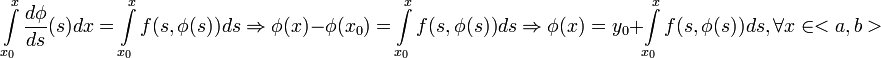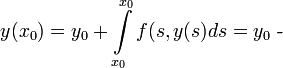Как найти частное неоднородное решение системы - Исправление недочетов и поиск решений вместе с Examum.ru

Структура общего решения системы уравнений

Однородная система линейных уравнений

$begin{cases}a_{11}x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+a_{22}x_2+ldots+ a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{m1}x_1+a_{m2}x_2+ldots+a_{mn}x_n=0,end{cases}$ или Ax=o

всегда совместна, так как имеет тривиальное решение x_1=x_2=ldots=x_n=0~(x=o) . Если ранг матрицы системы равен количеству неизвестных (operatorname{rg}A=n) , то тривиальное решение единственное. Предположим, что r=operatorname{rg}A<n . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица (Amid o) однородной системы при элементарных преобразованиях строк приводится к упрощенному виду (A'mid o) , т.е. b'_1=b'_2=ldots=b'_r=0 . Поэтому из (5.11) получаем общее решение однородной системы уравнений:

$begin{cases}x_1=-a'_{1,r+1}x_{r+1}-ldots-a'_{1n}x_n,\phantom{ x_1=-a'_{1,r+1}}vdots\ x_r=-a'_{r,r+1}x_{r+1}-ldots-a'_{rn}x_n.end{cases}$

(5.13)

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы varphi_1,varphi_2,ldots,varphi_k — решения однородной системы уравнений, то любая их линейная комбинация alpha_1varphi_1+alpha_2varphi_2+ ldots+alpha_kvarphi_k также является решением однородной системы.

В самом деле, из равенств Avarphi_1=o,~ Avarphi_2=o,~ldots,~ Avarphi_k=o следует, что

$Acdot! begin{pmatrix}alpha_1cdotvarphi_1+ alpha_2cdotvarphi_2+ ldots+alpha_kcdotvarphi_k end{pmatrix}= alpha_1cdot Acdotvarphi_1+ alpha_2cdot Acdotvarphi_2+ ldots+alpha_kcdot Acdotvarphi_k=o,$

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет (n-r) линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем (n-r) частных решений $varphi_1,varphi_2,ldots,varphi_{n-r}$ , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

$begin{aligned} mathsf{1)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=0colon~~ varphi_1= begin{pmatrix}-a'_{1,r+1}&cdots&-a'_{r,r+1}&1&0&cdots&0end{pmatrix}^T;\[5pt] mathsf{2)}&quad x_{r+1}=0,~x_{r+2}=1,~ldots,~x_n=0colon~~ varphi_2= begin{pmatrix}-a'_{1,r+2}&cdots&-a'_{r,r+2}&0&1&cdots&0end{pmatrix}^T;\[5pt] mathsf{n-r)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=1colon~~ varphi_{n-r}= begin{pmatrix}-a'_{1n}&cdots&-a'_{rn}&0&0&cdots&1end{pmatrix}^T. end{aligned}$

Получим (n-r) решений

$varphi_1= begin{pmatrix}-a'_{1,r+1}\vdots\-a'_{r,r+1}\1\0\vdots\0end{pmatrix}!,quad varphi_2= begin{pmatrix}-a'_{1,r+2}\vdots\-a'_{r,r+2}\0\1\vdots\0end{pmatrix}!,quad ldots,quad varphi_{n-r}= begin{pmatrix}-a'_{1n}\vdots\-a'_{rn}\0\0\vdots\1end{pmatrix}!.$

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние (n-r) ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних (n-r) строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен (n-r) . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность (n-r) линейно независимых решений $varphi_1,varphi_2,ldots,varphi_{n-r}$ однородной системы называется фундаментальной системой (совокупностью) решений.

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества (n-r) линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если $varphi_1,varphi_2,ldots,varphi_{n-r}$ — фундаментальная система решений однородной системы уравнений (5.4), то столбец

$x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}$

(5.14)

при любых значениях произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных $C_{1},C_{2},ldots,C_{n-r}$ , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

$H=begin{pmatrix}varphi_1&cdots&varphi_{n-r}&xend{pmatrix}= begin{pmatrix}varphi_{11}&cdots&varphi_{1,n-r}&x_1\ vdots&ddots&vdots&vdots\ varphi_{r1}&cdots&varphi_{r,n-r}&x_r\ varphi_{r+11}&cdots&varphi_{r+1,n-r}&x_{r+1}\ vdots&ddots&vdots&vdots\ varphi_{n1}&cdots&varphi_{n,n-r}&x_n end{pmatrix}!.$

Найдем ранг этой матрицы. Так как первые (n-r) столбцов линейно независимы, то operatorname{rg}Hgeqslant n-r . Так как каждый из столбцов матрицы является решением системы A'x=o , то по первой формуле из (5.13) получаем

$begin{aligned} varphi_{11}&= -a'_{1,r+1}varphi_{r+11}-ldots- a'_{1n}varphi_{n1},\ cdots & cdotscdotscdotscdots\[2pt] varphi_{1,n-r}&= -a'_{1,r+1}varphi_{r+1,n-r}-ldots- a'_{1n}varphi_{n,n-r},\[2pt] x_1&= -a'_{1,r+1}x_{r+1}-ldots- a'_{1n}x_n. end{aligned}$

Следовательно, первая строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, operatorname{rg}Hleqslant n-r , так как после вычеркивания в матрице будет всего (n-r) строк. Таким образом, operatorname{rg}H=n-r . Значит, есть базисный минор матрицы , который расположен в первых (n-r) ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа $C_1,C_2,ldots,C_{n-r}$ , что

$x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}.$

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных (r=operatorname{rg}A=n) , то система имеет единственное тривиальное решение x-o и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных (operatorname{rg}A<n) , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему $varphi_1, varphi_2, ldots,varphi_{n-r}$ решений однородной системы. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

Замечания 5.3

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица $Phi=begin{pmatrix}varphi_1&varphi_2&cdots&varphi_{n-r} end{pmatrix}$ столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

x=Phicdot c , где $c=begin{pmatrix}C_1&cdots&C_{n-r} end{pmatrix}^T$ — столбец произвольных постоянных.

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

$begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&0\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&0\ 0&0&cdots&0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix} E_r!!&vline!!&A'_{rtimes(n-r)}!!&vline!!&o\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Тогда блочная матрица $Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}$ размеров ntimes(n-r) является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

$begin{cases}x_1+x_2+2x_3+x_4=0,\[2pt] 2x_1+3x_2+x_4=0,\[2pt] 3x_1+4x_2+2x_3+2x_4=0. end{cases}$

Решение. 1. Составляем расширенную матрицу системы

$begin{pmatrix}Amid oend{pmatrix}= begin{pmatrix} 1&1&2&1!!&vline!!&0\ 2&3&0&1!!&vline!!&0\ 3&4&2&2!!&vline!!&0 end{pmatrix}!.$

2-4. Используя элементарные преобразования над строками матрицы (Amid o) , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

$begin{pmatrix}A'mid oend{pmatrix}= begin{pmatrix} 1&0&6&2!!&vline!!&0\ 0&1&-4&-1!!&vline!!&0\ 0&0&0&0!!&vline!!&0 end{pmatrix}!.$

Пункт 3 метода Гаусса пропускаем.

5. Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные. Записываем формулу (5.13) общего решения однородной системы

$begin{cases}x_1=-6x_3-2x_4,\x_2=4x_3+x_4.end{cases}$

6. Находим фундаментальную систему решений. Так как n=4 и r=operatorname{rg}A=2 , надо подобрать n-r=2 линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

1) если x_3=1,~x_4=0 , то x_1=-6,~x_2=4 ;

2) если x_3=0,~x_4=1 , то x_1=-2,~x_2=1 .

В результате получили фундаментальную систему решений

$varphi_1=begin{pmatrix}-6\4\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-2\1\0\1end{pmatrix}!.$

7. Записываем общее решение однородной системы по формуле (5.14):

$x=C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot!begin{pmatrix}-2\1\0\1end{pmatrix}!.$

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, x_3=1,~x_4=2 и x_3=2,~x_4=3 . Тогда получим другую фундаментальную систему решений

$varphi_1=begin{pmatrix}-10\6\1\2end{pmatrix}!,quad varphi_2=begin{pmatrix}-18\11\2\3end{pmatrix}$ и общее решение системы $x=C_1cdot! begin{pmatrix}-10\6\1\2end{pmatrix}+ C_2cdot! begin{pmatrix}-18\11\2\3end{pmatrix}!.$

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему Ax=b и соответствующую ей однородную систему Ax=o . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств Ax=b и Ay=b следует, что A(x-y)=Ax-Ay=b-b=o .

2. Пусть x^H — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

x=x^H+x^O , где x^O — решение однородной системы.

В самом деле, для любого решения неоднородной системы разность x-x^H по свойству 1 является решением однородной системы, т.е. x^O=x-x^H — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть x^H — решение неоднородной системы, а $varphi_1,varphi_2,ldots,varphi_{n-r}$ — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

$x=x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2+ldots+ C_{n-r}cdotvarphi_{n-r}$

(5.15)

при любых значениях [i]произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение x^H неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему $varphi_1,varphi_2,ldots,varphi_{n-r}$ ее решений. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

Замечания 5.4

1. Используя фундаментальную матрицу Phi однородной системы Ax=o , решение неоднородной системы Ax=b можно представить в виде

x=x^H+Phicdot c,

где x^H — частное решение неоднородной системы, а $c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T$ — столбец произвольных постоянных.

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

$begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&b'_1\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&b'_2\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&b'_r\ 0&0&cdots& 0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots& vdots&ddots& vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix}E_r!!& vline!!&A'_{rtimes(n-r)}!!&vline!!&b'_{rtimes1}\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Тогда блочная матрица $Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}$ оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец $x^H=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}$ является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

$x=x^H+Phicdot c=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}+begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}!cdot c,$

(5.16)

где $c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T$ — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

$begin{cases}x_1+ x_2+2x_3+x_4=1,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=1.end{cases}$

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

$begin{cases}x_1=3-6x_3-2x_4,\x_2=-2+4x_3+x_4.end{cases}$

Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные.

6. Полагая x_3=0,~x_4=0 , получаем частное решение неоднородной системы $x^H=begin{pmatrix}3&-2&0&0end{pmatrix}^T$ .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

$varphi_1=begin{pmatrix}-6&4&1&0end{pmatrix}^T,qquad varphi_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T.$

8. Записываем по формуле (5.15) общее решение неоднородной системы

$x=x^H+C_1cdotvarphi_1+C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.$

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

$begin{pmatrix}Amid bend{pmatrix}= begin{pmatrix}1&0&6&2!!&vline!!&3\ 0&1&-4&-1!!&vline!!&-2\ 0&0&0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} 1&0!!& vline!!&6&2!!&vline!!&3\ 0&1!!&vline!!&-4&-1!!&vline!!&-2\hline 0&0!!&vline!!& 0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} E_2!!&vline!!&A'_{2times2}!!& vline!!& b'_{2times1}\ O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Записываем частное решение неоднородной системы

$x^H= begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}= begin{pmatrix}dfrac{b'_{2times1}}{o_{2times1}}end{pmatrix}= begin{pmatrix}3\-2\0\0 end{pmatrix}$

и составляем фундаментальную матрицу:

$Phi= begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}= begin{pmatrix}dfrac{-A'_{2times2}}{E_2}end{pmatrix}= begin{pmatrix}-6&-2\4&1\1&0\ 0&1end{pmatrix}= begin{pmatrix}varphi_1&varphi_2end{pmatrix}!.$

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

$x=x^H+Phicdot! begin{pmatrix}C_1\C_2end{pmatrix}= x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0 end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.$

которое совпадает с ранее полученным.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Вопрос
№12

Структура
общего решения неоднородной системы
уравнений

Ранее
была выведена формула
(5.11) общего решения системы линейных
уравнений.
Получим другую форму записи, отражающую
структуру множества решений.

Рассмотрим
неоднородную систему и
соответствующую ей однородную систему .
Между решениями этих систем имеются
связи, выражающиеся следующими свойствами.

Свойства
решений неоднородной системы уравнений

1. Разность
двух решений и неоднородной
системы есть решение однородной системы.

Действительно,
из равенств и следует,
что .

2. Пусть —
решение неоднородной системы. Тогда
любое решение неоднородной
системы можно представить в виде

, где —
решение однородной системы.

В
самом деле, для любого решения  неоднородной
системы разность  по
свойству 1 является решением однородной
системы, т.е.  —
решение однородной системы.

Теорема
5.4 о структуре общего решения неоднородной
системы.

Пусть —
решение неоднородной системы, а —
фундаментальная система решений
соответствующей однородной системы
уравнений. Тогда столбец

(5.15)

при
любых значениях [i]произвольных
постоянных  является
решением неоднородной системы, и,
наоборот, для каждого решения  этой
системы найдутся такие значения
произвольных постоянных ,
при которых это решение  удовлетворяет
равенству (5.15).[/i]

Говорят,
что общее решение неоднородной системы
есть сумма частного решения неоднородной
системы и общего решения соответствующей
однородной системы.

Доказательство
теоремы вытекает из свойств 1, 2 и теоремы
5.3.

Алгоритм
решения неоднородной системы уравнений

1-5. Выполнить
первые 5 пунктов метода
Гаусса решения
системы уравнений и получить формулу
общего решения неоднородной системы
вида (5.11).

6. Найти
частное решение неоднородной
системы, положив в (5.11) все свободные
переменные равными нулю.

7. Записав
формулы (5.13) общего решения соответствующей
однородной системы, составить
фундаментальную систему ее
решений. Для этого подставить в (5.13)
последовательно стандартных
наборов значений свободных переменных,
в которых все переменные равны нулю, за
исключением одной, равной единице.

8. Записать
общее решение неоднородной системы по
формуле (5.15).

Замечания
5.4

1. Используя
фундаментальную матрицу однородной
системы ,
решение неоднородной системы можно
представить в виде

где —
частное решение неоднородной системы,
а —
столбец произвольных постоянных.

2. Если
базисный минор матрицы  расположен
в левом верхнем углу (в первых  строках
и первых  столбцах),
то упрощенный вид расширенной матрицы
(5.9) неоднородной системы можно представить
в виде блочной матрицы

Тогда
блочная матрица оказывается
фундаментальной (см. п.3 замечаний 5.3), а
столбец является
частным решением неоднородной системы
(в этом можно убедиться, подставляя в
(5.11) нулевой набор свободных переменных).
Используя блочные матрицы, общее решение
(5 15) неоднородной системы можно представить
в виде

(5.16)

где —
столбец произвольных постоянных.
Полученную формулу можно считать вторым
способом решения
неоднородной системы.

Пример
5.5. Найти
структуру (5.15) общего решения неоднородной
системы

Решение. 1-5.
Первые 5 пунктов метода Гаусса выполнены
при решении примера 5.3, где получены
формулы общего решения неоднородной
системы:

Переменные —
базисные, а —
свободные.

6.
Полагая ,
получаем частное решение неоднородной
системы .

7.
Находим фундаментальную систему решений
однородной системы (см. пример 5.4):

8.
Записываем по формуле (5.15) общее решение
неоднородной системы

Искомая
структура множества решений найдена.

Получим
формулу общего решения вторым
способом,
используя п.2 замечаний 5.4. При решении
примера 5.3 расширенная матрица системы
была приведена к упрощенному виду.
Разбиваем ее на блоки:

Записываем
частное решение неоднородной системы

и
составляем фундаментальную матрицу:

По
формуле (5.16) получаем общее решение
неоднородной системы, которое преобразуем
к виду (5.15):

которое
совпадает с ранее полученным.

Метод вариации постоянных

Рассмотрим
неоднородное уравнение -го
порядка

,

(1)

где
коэффициенты и
правая часть —
заданные непрерывные функции на
интервале .

Допустим,
что нам известна фундаментальная система
решений соответствующего
однородного уравнения

(2)

Как
мы показали в § 1.15 (формула (6)), общее
решение уравнения (1) равно сумме общего
решения уравнения (2) и какого-либо
решения уравнения (1).

Решение
неоднородного уравнения (1) можно получить
методом вариации постоянных, если
известно общее решение однородного
уравнения (2). Разъясним этот метод на
примере уравнения порядка.

Итак,
пусть задано линейное уравнение третьего
порядка

.

(3)

Пусть
общее решение соответствующего
однородного уравнения есть

,

(4)

где —
линейно независимые решения уравнения
(2)

Будем
искать решение неоднородного уравнения
(3) в виде суммы (4), где —
некоторые непрерывно дифференцируемые
функции, которые надо найти. Наложим на
искомые функции два
условия

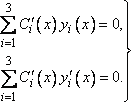
(5)

Тогда
будет

Подставив
эти производные и саму функцию в
(3), получим

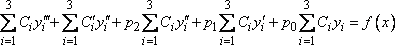
или

Но
выражения в скобках в левой части этого
равенства равны нулю, поэтому

.

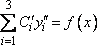
(6)

Мы
получили уравнение (6) и два уравнения
(5) с коэффициентами и
правой частью ,
которые непрерывны на .
Эти три уравнения образуют линейную
алгебраическую систему относительно
неизвестных с
определителем, не равным нулю, потому,
что это есть определитель Вронского
для фундаментальной системы решений .
Поэтому данная система имеет единственное
решение

где —
непрерывные на функции.
Отсюда

.

(7)

При
этом функции имеют
на непрерывную
производную. Следовательно, частное
решение неоднородного уравнения (1)
имеет вид

где
функции определяются
равенствами (7).

Пример, —
корни характеристического уравнения;
общее решение однородного уравнения .

Найдем
частное решение неоднородного уравнения
методом вариации постоянных и .
Составим систему 5), (6):

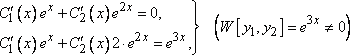
Решая
систему, имеем .
Отсюда и
частное решение

Таким
образом, общее решение исходного
уравнения

Вопрос №13 Определения

Задача
Коши, , —
начальные данные:

Решением
задачи Коши является функция, определённая
на интервале <a,b>, включающем ,
являющаяся решением уравнения (1) и
удовлетворяющая начальному условию
(2).

Определение. Решением
интегрального уравнения:

является
функция ,
которая определена на <a,b> и

(непрерывна)
<a,b>
подстановка превращает
уравнение (3) в тождество.

Лемма. Функция является
решением задачи Коши тогда и только
тогда, когда она является решением
интегрального уравнения.

Доказательство. Пусть —
решение задачи Коши и

Проинтегрируем
тождество от до :

Теперь
пусть —
решение интегрального уравнения,
покажем, что она есть решение дифф.
уравнения и удовлетворяет начальному
условию. Для этого вначале подставим в
(3) :

Продифференцируем
(3) и получим (1)

Определение. ,
заданная на ,
удовлетворяет условию Липшица, если

Заметим,
что если функция удовлетворяет условию
Липшица, то она является равномерно
непрерывной на (для
док-ва замечания надо взять )

Определение. Последовательность
функций является
равномерно ограниченной если

Определение. Последовательность
функций называется
равнестепенно непрерывной, если

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

(схема 18)

Пусть задана неоднородная
система линейных алгебраических уравнений размерности m×n.

Матрицаназывается
расширенной матрицей системы, если наряду с коэффициентами при
неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m×(n+1).

Исследование любой системы линейных алгебраических
уравнений начинается с преобразования ее расширенной матрицы методом Гаусса, который основан
на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае
преобразования производятся по
столбцам).

Элементарные преобразования приводят первоначальную
систему к системе, ей эквивалентной. Системы
называются
эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется
наивысший порядок отличных от нуля ее миноров. Элементарные преобразования
ранга матрицы не меняют.

На вопрос о наличии
решений у неоднородной системы линейных
уравнений отвечает следующая теорема.

Теорема 1.3
(теорема Кронекера-Капелли). Неоднородная система линейных алгебраических
уравнений совместна тогда и только тогда, когда ранг расширенной матрицы
системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после
метода Гаусса, через r (соответственно, в системе остается r
уравнений). Эти строки матрицы называются
базисными.

Если r=n, то
система имеет единственное решение (является совместной определенной), ее
матрица элементарными преобразованиями приводится к треугольному виду. Такую
систему можно решить также методом Крамера и с помощью обратной матрицы.

Если r<n (количество переменных в системе больше количества уравнений), матрица элементарными преобразованиями
приводится к ступенчатому виду. Такая
система имеет множество решений и является совместной неопределенной. В данном
случае для нахождения решений системы необходимо выполнить ряд операций.

1.
Оставить в левых
частях уравнений системы r неизвестных (базисные переменные), остальные n—r неизвестных перенести в правые части (свободные
переменные). После разделения переменных на базисные и свободные
система принимает вид:

. (1.10)

2. Из коэффициентов при базисных переменных составить
минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну
из базисных переменных следует заменить на свободную; полученный базисный минор
снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые
части уравнений их свободными членами, найти выражение базисных переменных
через свободные в общем виде. Полученный при этом упорядоченный набор
переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные
значения, вычислить соответствующие значения базисных переменных. Получаемый
при этом упорядоченный набор значений всех переменных называется частным
решением системы, соответствующим данным значениям свободных
переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное
решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов
переменных системы (1.10) равно числу
сочетаний из n элементов по r элементов C_n^r. Так как каждому базисному набору переменных соответствует
свое базисное решение, следовательно, количество базисных решений у системы
также
равно C_n^r.

Пусть строки матрицы обозначены соответственно l₁;l₂;…;l_n.
Строка l называется линейной комбинацией строк l₁;l₂;…;l_n матрицы, если она равна сумме произведений
этих строк на произвольные действительные числа, то есть ,.

Однородная система уравнений всегда совместна, так как
имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная
система n линейных уравнений с n переменными имела ненулевые решения, необходимо и
достаточно, чтобы ее главный определитель ∆
был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n
неизвестных (r<n). В этом случае исследование однородной системы
уравнений на общее и частные решения проводится аналогично исследованию
неоднородной системы. Решения однородной системы уравнений обладают важным
свойством: если известны два различных решения однородной системы линейных алгебраических
уравнений, то их линейная комбинация также является решением этой системы.
Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений
представляет собой сумму общего решения соответствующей однородной системы и
некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней
элементарные преобразования:

Так как r(A)=2 и , то по теореме 1.3
(Кронекера-Капелли) заданная система линейных алгебраических уравнений
совместна. Количество переменных n=2, т.е. r<n, значит,
система является неопределённой.
Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов
переменных: {x₁;x₂}, {x₁;x₃}, {x₁;x₄}, {x₂;x₃}, {x₂;x₄}, {x₃;x₄}. Рассмотрим один из них {x₁;x₂}. Тогда
систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

Вспомогательные определители

По
формулам (1.6) имеем

Данное выражение базисных переменных через свободные
представляет собой общее решение
системы:

При конкретных значениях свободных переменных из
общего решения получаем частное решение системы. Например, частное решение соответствует
значениям свободных переменных x₃=x₄=17. При x₃=0 x₄=0 получаем базисное решение системы

Вопросы для самопроверки

Источник

Найти решение системы дифференциальных уравнений

СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ

Основные понятия
Метод исключения
1. Пример 1
2. Пример 2
3. Пример 3
Метод Эйлера
1. Пример 4

Основные понятия

В данной статье рассмотрим линейные системы дифференциальные уравнений, которые делятся на два вида: однородные и неоднородные. В общем виде они записываются следующим образом $$begin{cases} frac{dx}{dt} = a_1 x(t) + b_1 y(t) + f_1(t) \ frac{dy}{dt} = a_2 x(t) + b_2 y(t) + f_2(t) end{cases},$$где $a_1, b_1, c_1, a_2$ коэффициенты, функции $f_1(t)$ и $f_2(t)$ могут отсутствовать, либо быть константами, $x(t),y(t)$ неизвестные функции, которые требуется найти в качестве решения системы ДУ. Напоминаем, что аналогичная запись $frac{dx}{dt} = x'(t)$ и $frac{dy}{dt} = y'(t)$.

Если хотя бы один из коэффициентов $f_1(t)$ или $f_2(t)$ не равен нулю, то система называется неоднородной. Если $f_1(t) = f_2(t) = 0$, то система однородная.

Решением системы дифференциальных уравнений называется пара функций $y(t), x(t)$, подстановка которых в систему обращает её в тождество.

Разберём два основных способа решения линейных систем дифференциальных уравнений: метод исключения и метод Эйлера.

Метод исключения

Суть метода в том, что два уравнения сводятся к одному линейному дифференциальному уравнению. Для этого есть примерный алгоритм:

Находим производную одного из уравнений системы, например, $y»_t$
В получившейся производной исключаем всё что связано с $x$
Решаем линейное дифференциальное уравнение относительно $y(t)$
Подставляем получившийся $y(t)$ в одно из уравнений системы, чтобы найти $x(t)$

Пример 1

Решить систему дифференциальных уравнений методом исключения $$begin{cases} frac{dx}{dt} =y-7 \ frac{dy}{dt} = -2x — 3y end{cases}.$$

Решение

Применим метод исключения, чтобы из двух уравнений получить одно. Берем первое уравнение и дифференцируем его по $t$. $$frac{d^2 x}{dt^2} = frac{dy}{dt}$$ В получившееся уравнения вместо $frac{dy}{dt}$ подставим второе уравнение системы. $$frac{d^2 x}{dt^2} = -2x — 3y$$ Теперь нужно избавиться от $y$, чтобы остались только $x$, и тогда можно будет решить дифференциальное уравнение относительно $x(t)$. Для этого берём первое уравнение системы и получаем из него $$y = frac{dx}{dt}+7.$$ Продолжаем решение с учётом полученного $y$ $$frac{d^2 x}{dt^2} = -2x — 3 (frac{dx}{dt}+7).$$ После раскрытия скобок и преобразований получаем уравнение $$frac{d^2 x}{dt^2} + 3frac{dx}{dt} + 2x = 21.$$ Это линейное неоднородное дифференциальное уравнение второго порядка. Решение его будем искать в виде $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$.

Сначала находим общее решение однородного уравнения $x_text{о.о.}$. Для этого отбрасываем правую часть уравнения и составляем характеристический многочлен и находим его корни. $$lambda^2 + 3lambda + 2 = 0,$$ $$lambda_{1,2} = frac{-3pm sqrt{9-4cdot 1 cdot 2}}{2} = frac{-3pm 1}{2},$$ $$lambda_1 = -1, lambda_2 = -2.$$ Итак, записываем $$x_text{о.о.} = C_1 e^{-t} + C_2 e^{-2t}.$$

Искать частное решение $x_text{ч.н.}$ будем искать методом подбора правой части исходного неоднородного линейного дифференциального уравнения. В данном случае в правой части стоит константа, значит подбор будет в виде $x_text{ч.н.} = A$. Находим первую и вторую производную и подставляем в исходное решаемое уравнение. $$x’_text{ч.н.} = 0, x»_text{ч.н.} = 0$$ $$0 + 3 cdot 0 + 2 A = 21 Rightarrow A = frac{21}{2}.$$ Значит, $x_text{ч.н.} = frac{21}{2}$.

Записываем окончательно, что $$x(t) = x_text{о.н.} = x_text{о.о.} + x_text{ч.н.} = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2}$$

Теперь зная $x(t)$ можно получить $y(t)$. Для этого нужно вернуться к началу решения и вспомнить, что мы выражали $y = frac{dx}{dt}+7$. Таким образом осталось в него подставить полученное решение $x(t)$ $$y(t) = (C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2})’ + 7 = -C_1 e^{-t} — 2C_2 e^{-2t} + 7$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$begin{cases} x(t) = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2} \ y(t) = -C_1 e^{-t} — 2C_2 e^{-2t} + 7 end{cases}$$

Пример 2

Найти решение системы дифференциальных уравнений $$begin{cases} x’ = -2y+3t \ y’ = 2x+4 end{cases},$$ где $x(t),y(t)$ — искомые функции, $t$ — независимая переменная.

Решение

Решаем методом исключения, то есть два уравнения приводим к одному. Берем производную первого уравнения по $t$. $$x» = (-2y+3t)’_t = -2y’+3$$ Знаем чему равен $y’$ из второго уравнения системы и поэтому его подставляем в получившееся последнее уравнение. $$x» = -2(2x+4)+3 = -4x — 8 + 3 = -4x — 5$$

Переписываем последнее получившееся уравнение в форме линейного неоднородного дифференциального уравнения второго порядка. $$x» + 4x = -5$$

Общее решение этого уравнения найдем в качестве суммы общего решения однородного уравнения и частного решения неоднородного $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Итак, составляем характеристический многочлен и находим его корни. $$lambda^2 + 4 = 0$$ $$lambda_1 = -2i, lambda_2 = 2i.$$ Так как получились комплексные корни, то общее решение записывается следующим образом $$x_text{о.о.} = C_1cos 2t + C_2 sin 2t.$$ Осталось найти $x_text{ч.н.}$. Для этого воспользуемся методом подбора правой части. Так как она представляет собой константу, то значит $x_text{ч.н.} = A$. Отсюда следует, что $x»_text{ч.н.} = 0$. Подставляя эти данные в дифференциальное уравнение получаем значение $A$. $$0 + 4A = -5,$$ $$A = -frac{5}{4}.$$

Таким образом можно записать, что $$x(t) = x_text{о.о.} + x_text{ч.н.} = C_1cos 2t + C_2 sin 2t -frac{5}{4}.$$

Осталось найти функцию $y(t)$. Для этого выразим её из первого уравнения и подставим ранее полученный $x(t)$. $$y = frac{3}{2}t — frac{x’}{2},$$ $$y = frac{3}{2}t — frac{1}{2}(C_1cos 2t + C_2 sin 2t -frac{5}{4})’ = $$ $$ = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t.$$

Ответ

$$begin{cases} x(t) = C_1cos 2t + C_2 sin 2t -frac{5}{4} \ y(t) = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t end{cases}$$

Пример 3

Найти общее и частное решение системы дифференциальных уравнений $$begin{cases} frac{dx}{dt} = 2x+y \ frac{dy}{dt} = x+2y end{cases}, x(0)=1, y(0)=3$$

Решение

Берем второе уравнение и находим его производную по $t$. $$frac{dy^2}{dt^2} = frac{dx}{dt}+2frac{dy}{dt}$$ В полученное равенство вместо frac{dx}{dt} подставим первое уравнение системы. $$frac{dy^2}{dt^2} = 2x+y + 2frac{dy}{dt}$$ Осталось избавиться от $x$. Для этого выразим его из второго уравнения системы и подставим в последнее полученное уравнение. $$frac{dy^2}{dt^2} = 2(frac{dy}{dt} — 2y) + y + 2frac{dy}{dt}$$ Раскроем скобки и перенесем всё в левую сторону. Затем запишем для удобства $frac{dy}{dt} = y’$. $$y» — 4y’ + 3y = 0$$

Получившееся дифференциальное уравнение называется однородным линейным ду второго порядка. Для его решения составляем характеристический многочлен и находим его корни. $$lambda^2 — 4lambda + 3 = 0,$$ $$lambda_{1,2} = frac{4pm sqrt{16 — 4 cdot 1 cdot 3}}{2} = frac{4pm 2}{2},$$ $$lambda_1 = 1, lambda_2 = 3.$$ Общее решение такого уравнения записывается в виде $$y = C_1 e^{3t} + C_2e^{t}.$$

Так как мы нашли $y(t)$, то теперь можем найти $x(t)$. Для этого подставляем $y(t)$ во второе уравнение системы и выражаем $x(t)$. $$x(t) = frac{dy}{dt} — 2y = (C_1 e^{3t} + C_2e^{t})’ — 2(C_1 e^{3t} + C_2e^{t})$$ После раскрытия скобок и упрощения остаётся $$x(t) = 3C_1 e^{3t} + C_2 e^t — 2C_1 e^{3t} — 2C_2 e^t = C_1 e^{3t} — C_2 e^t.$$ Вот таким образом находится общее решение системы дифференциальных уравнений $$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}.$$

По условию задания необходимо кроме общего найти частное решение. Для этого берем дополнительные условия из задачи $x(0)=1, y(0)=3$ и подставляем в полученное общее решение, чтобы вычислить константы $C_1$ и $C_2$. $$begin{cases} x(0) = C_1e^{0}-C_2e^0 = 1 \ y(0) = C_1 e^0 + C_2 e^0 = 3 end{cases},$$ $$ begin{cases} C_1-C_2 = 1 \ C_1 + C_2 = 3 end{cases} Rightarrow begin{cases} C_1 = 2 \ C_2 = 1 end{cases}.$$ Теперь зная постоянные можно записать частное решение системы дифференциальных уравнений $$begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}.$$

Ответ

$$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}, begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}$$

Метод Эйлера

Примерный алгоритм решения по данному методу следующий:

Построить матрицу $A$ из коэффициентов дифференциальных уравнений
Найти собственные значения $lambda$ и векторы матрицы $overline{x}$
Записать общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 $$

Рассмотрим данный метод решения на конкретном примере, так как практика учит лучше, чем теория.

Пример 4

Решить систему дифференциальных уравнений методом эйлера $$begin{cases} x’ = 2x+y \ y’ = 3x+4y end{cases}.$$

Решение

Первым делом нужно составить матрицу, элементы которой равны коэффициентам из правой части системы дифференциальных уравнений. $$A = begin{pmatrix} 2&1 \ 3&4 end{pmatrix}$$

Далее нужно найти собственные значения матрицы. Для этого необходимо составить характеристический многочлен и вычислить его корни. $$|A-lambda E| = 0 Rightarrow begin{vmatrix} 2 — lambda & 1 \ 3 & 4-lambda end{vmatrix} = 0$$

Раскрываем определитель два на два и решаем квадратное уравнение. $$(2-lambda)(4-lambda)-3 = 0,$$ $$8-2lambda -4lambda+lambda^2 — 3 = 0,$$ $$lambda^2 — 6lambda + 5 = 0,$$ $$lambda_{1,2} = frac{6pm sqrt{36-4 cdot 5}}{2} = frac{6pm 4}{2},$$ $$lambda_1 = 1, lambda_2 = 5.$$ Зная собственные значения матрицы получим собственные векторы матрицы по формуле $(A-lambda E)overline{x} = 0$.

1) Для $lambda_1 = 1$ имеем $$(A-lambda_1 E)overline{x}_1 = 0 Rightarrow begin{cases} x_1 + x_2 = 0 \ 3x_1 + 3x_2 = 0 end{cases}$$ Видим, что после сокращения второго уравнения на 3 получится, что первое уравнение равно второму. $$x_1 + x_2 = 0 Rightarrow x_1 = -x_2$$ Так как $x_2$ свободный, то положим его $x_2 = 1$. Тогда $x_1 = -1$. Отсюда следует, что первый собственный вектор равен $$overline{x}_1 = begin{pmatrix} -1 \ 1 end{pmatrix}.$$

2) Для $lambda_2 = 5$ имеем $$(A-lambda_2 E)overline{x}_2 = 0 Rightarrow begin{cases} -3x_1 + x_2 = 0 \ 3x_1 — x_2 = 0 end{cases}$$ Замечаем, что первое уравнение одно и тоже что второе, если домножить на (-1) одно из них. $$3x_1 — x_2 = 0 Rightarrow x_1 = frac{x_2}{3}$$ Так как $x_2$ свободный, то зададим его $x_2 = 3$. Таким образом $x_1 = 1$. Из этих значений получаем второй собственный вектор $$overline{x}_2 = begin{pmatrix} 1 \ 3 end{pmatrix}.$$

Находим общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 = $$ $$ = C_1 e^t begin{pmatrix} -1 \ 1 end{pmatrix} + C_2 e^{5t} begin{pmatrix} 1\3 end{pmatrix} = begin{pmatrix} -C_1 e^t \ C_1e^t end{pmatrix} + begin{pmatrix} C_2 e^{5t} \ 3C_2 e^{5t} end{pmatrix} = $$ $$ = begin{pmatrix} -C_1 e^t + C_2 e^{5t} \ C_1 e^t + 3C_2 e^{5t} end{pmatrix} Rightarrow begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$

Ответ

$$begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$

Источник