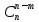Как найти частное решение интеграла

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 — ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 — это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n — 1 ) ( x 0 ) = f n — 1

где f 0 ; f 1 ; f 2 ; . . . ; f n — 1 — это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 — заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) — это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.

Общий и частный интеграл

Определение 1.15. Частное решение дифференциального уравнения, заданное неявно соотношением

называется частным интегралом.

Определение 1.16. Соотношение вида

определяющее общее решение дифференциального уравнения у = (fix, С) как неявную функцию, называется общим интегралом.

Из соотношения (1.43) при помощи выбора параметра С может быть получен любой частный интеграл, то сеть может быть получено уравнение любой интегральной кривой.

11 р нмер 1.10. Рассмотрим уравнение

Условия теоремы Коши выполнены всюду, за исключением прямой у = 0. Из (1.44) получаем при у * 0:

Таким образом, общий интеграл уравнения имеет вид

Замечание 1.19. Уравнения (1.45) определяют на плоскости семейство концентрических окружностей с центром в точке (0, 0). Эта точка является изолированной особой точкой уравнения (1.44) (поскольку через нес нс проходит ни одной интегральной кривой) и называется центром.

Особое решение

Определение 1.17. Если интегральная кривая дифференциального уравнения состоит только из особых точек, то такая кривая называется особым решением уравнения.

Особое решение нельзя получить из общего решения.

Пр нмер 1.11. Рассмотрим уравнение

Выше, при решении примера 1.6, было установлено, что решениями этого уравнения являются семейство кубических парабол у = (х — С) 3 и прямая у = 0. Следовательно, через любую точку (С, 0) оси Ох проходят, по крайней мерс, две интегральные кривые: ось Ох и парабола у = (х — С) 3 . Это показывает, что точки оси Ох являются особыми точками данного уравнения, а функция у(л) = 0 — особым решением.

Определение 1.18. Линия на >носкости Оху называется огибающей однопараметрического семейства кривых, заданного уравнением Ф(.v, у,С) = 0, если в каждой своей точке она касается всех кривых данного семейства, и все кривые семейства каются этой линии.

Огибающая семейства Ф(х,у,С) = 0 определяется уравнениями

Очевидно, что если линия является огибающей семейства интегральных кривых некоторого дифференциального уравнения, то она сама является интегральной кривой, и, следовательно, определяет особое решение этого уравнения.

Замечание 1.20. В рассмотренном выше Примере 1.6 прямая y(jr) = 0 является огибающей семейства интегральных кривых уравнения

у’ = 3ify* и касается каждой кривой у = (х — С) > этого семейства в точке (С, 0). Так как эта прямая является также и особым решением, то у данного уравнения существуют следующие составные решения, склеенные из кусков «нижней» и «верхней» половин параболы у = (* — С) 3 и отрезков оси Ох:

Таким образом, что через любую точку вида (С; 0) в действительности проходит, нс две, а бесчисленное множество интегральных кривых уравнения у’ = 3^/у^. Таковыми, например, являются интегральные кривые вида (1.48), при условии, что C_l0 +оо — составные решения вида (1.47), а при С, —> -оо и С, —> +оо — особое решение у = 0.

Общее и частное решение общий и частный интеграл уравнения

В рассматриваемых ниже примерах требуется найти:

1. Общий и частный интегралы дифференциального уравнения;

2. Если это возможно, общее решение и частное решение, удовлетворяющее заданным начальным условиям.

, (Пр.1.1)

Данные примеры решаем по следующей схеме.

1. Разделяем переменные в (Пр.1.1) (считаем, что y ¹ 2):

, (Пр.1.2)

2. Интегрируем левую и правую части (Пр.1.2), вычисляем общий интеграл.

,

. (Пр.1.3)

Вычисляя данные интегралы, и записывая постоянную интегрирования в удобном для дальнейших преобразований виде, (переобозначаем С ® lnC), из (Пр.1.3) будем иметь

(Пр.1.4)

Отсюда получаем общий интеграл уравнения (Пр.1.1):

(Пр.1.5)

3. Вычисляем частный интеграл.

Чтобы найти выражение для частного интеграла, нужно найти значение С, соответствующее начальным условиям. Для этого подставляем в (Пр.1.5) вместо t =1, вместо y =1. При этом получим, что С=-3. Следовательно, частный интеграл уравнения (Пр.1.1) имеет вид:

(Пр.1.6)

4. Определяем общее решение.

В этом примере оно находится очень легко из общего интеграла (Пр.1.5):

(Пр.1.7)

5. Определяем частное решение.

Его можно найти, например, из общего решения (Пр.1.7), подставляя в него начальные условия и выражая постоянную С. Она, как и в пункте №3 оказывается равной С=-3. Следовательно, частное решение уравнения (Пр.1.1) даётся формулой:

(Пр.1.8)

Видно, что такое же выражение получается и из частного интеграла (Пр.1.6).

, (Пр.2.1)

Данные примеры решаем по следующей схеме.

1. Разделяем переменные в (Пр.2.1) (считаем, что sin (2 y ) ¹ 0):

, (Пр.2.2)

2. Интегрируем левую и правую части (Пр.2.2), вычисляем общий интеграл.

. (Пр.2.3)

Вычисляя данные интегралы, и записывая постоянную интегрирования в удобном для дальнейших преобразований виде (переобозначаем С ® lnC ), из (Пр.2.3) будем иметь

(Пр.2.4)

Отсюда получаем общий интеграл уравнения (Пр.2.1):

(Пр.2.5)

3. Вычисляем частный интеграл.

Чтобы найти выражение для частного интеграла, нужно найти значение С, соответствующее начальным условиям. Для этого подставляем в (Пр.2.5) вместо t =0, вместо . При этом получим, что С=8. Следовательно, частный интеграл уравнения (Пр.2.1) имеет вид:

(Пр.2.6)

4. Определяем общее решение.

Для этого из общего интеграла (Пр.2.5) выражаем y :

(Пр.2.7)

5. Определяем частное решение.

Для определения частного решения в данном случае используем частный интеграл (Пр.2.6). Выражая оттуда y , получим, что частное решение уравнения (Пр.2.1) даётся формулой:

(Пр.2.8)

, (Пр.3.1)

1. Разделяем переменные в (Пр.3.1) (считаем, что y ¹ -1):

, (Пр.3.2)

2. Интегрируем левую и правую части (Пр.3.2), вычисляем общий интеграл.

, (Пр.3.3)

Вычисляем данные интегралы:

,

В результате из (Пр.3.3) получаем общий интеграл уравнения (Пр.3.1):

(Пр.3.4)

3. Вычисляем частный интеграл.

Чтобы найти выражение для частного интеграла, нужно найти значение С, соответствующее начальным условиям. Для этого подставляем в (Пр.1.4) вместо t =2, вместо y =0. При этом получим, что . Следовательно, частный интеграл уравнения (Пр.3.1) имеет вид:

(Пр.3.6)

4. Общее решение.

Уравнение (Пр.3.4), определяющее общий интеграл, не может быть разрешено относительно y . Поэтому в данном примере в явном виде общее решение уравнения (Пр.3.1) получить невозможно. Следовательно, общий интеграл (Пр.3.4) задаёт общее решение уравнения (Пр.3.1) в неявном виде.

5. Частное решение.

Частное решение в явном виде также получено быть не может. Уравнение же (Пр.1.6) задаёт частное решение уравнения (Пр.3.1) в неявном виде.

1. Частное и общее решение. Частный и общий интеграл. Задачи Коши.

1. Общее
   решение – функция, зависящая от
   независимой переменной и постоянной
   Y, удовлетворяющая 2ум условиям:

1. Для
   любого значения C=C₀,
   Y = U (x, C₀).

2. C=C₀,
   Y = U (x₁,
   C₀),
   что данная функция удовлетворяет
   начальному условию y(x₀)
   = y₀.

1. Всякое
   общее решение, найденное при значении
   С равное С₀,
   называется частным решением диф.
   Уравнения.

Y
= u(x,
C₀)
— частное решение

1. Общим
   интегралом диф. Уравнения называется
   общее решение этого уравнения, записанное
   в неявном виде.

Ф
(x, y, c) = 0 — общий интеграл

1. Частным
   интегралом диф. Уравнения называется
   частное решение диф. Уравнения,
   записанное в неявном виде.

Ф
(х, у, с) = 0 – частный интеграл

Задача
Коши:

Нахождение
частного решения диф. Уравнения F (x, y,
c) = 0 удовлетворяющего начальному
условию.

y
(x₀)
= y₀

1. Дифференциальное уравнение с разделенными переменными и его решение.

Диф.
Уравнение с разделенными переменными
– уравнение вида:

f
(x) dx + u (y) dy = 0

∫ f(x)
dx + ∫ u (y) dy = C

F(x)
+ Ф(y)
= C
— общий интеграл

1. Дифференциальное уравнение с разделяющимися переменными и его решение.

Диф.
Уравнение с разделяющимися переменными
– это уравнение вида:

f₁(x)
* u₁(y)
dx + f₂(x)
* u₂(y)
dy = 0

Решение:

Разделим
переменные.

+
= 0+= 0

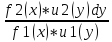
1. Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Линейные
диф. Уравнения 2ого порядка с постоянными
коэф. – это уравнение вида:

a₀*y”
+ a₁*y’
+ a₂*y
= f(x)

f(x)
0
– неоднородное

f(x)
= 0 – однородное

a₀*k²
+ a₁*k
+ a₂
= 0 — характерное уравнение

Структура
общего решения уравнения имеет вид:

y
= C₁*y₁
+ C₂*y₂

1. Элементы комбинаторики: размещения, перестановки, сочетания, свойство сочетаний.

Комбинаторика
– это математическая наука, изучающая
вопросы о том, сколько различных
комбинаций, подчиненных тем или иным
условием, можно составить.

1. Размещение.

Размещениями
из N по M элементов называют такие
соединения, в каждом из которых по M
элементов и различаются такие соединения
друг от друга только самими элементами
и их порядками.

A_n^m
= n (n-m+1)
=

1. Перестановка.

Перестановками
из N элементов называются такие
соединения, в каждом из которых по N
элементов U отличаются такие соединения
только порядком самих элементов.

P_n
=
=== n! P_n
= n!

1. Сочетание.

Сочетаниями
из N элементов по M называются такие
соединения, в каждом из которых по M
элементов и отличаются такие соединения
только самими элементами.

=
Свойство сочетания:=

1. Виды событий. Примеры.

Виды
событий:

1. Достоверное.
   Всегда произойдет при данном испытании.

Выстрел.

1. Невозможное.
   Никогда не произойдет при данном
   испытании.

Осечка.

1. Случайное.
   Может произойти, а может не произойти.

Попадание
и промах.

1. Совместные.
   Если появление одного события не
   исключает появление другого события.

Попадание
при 1 выстреле, не исключает промах при
2 выстреле.

1. Не
   совместные. Если появление одного из
   них исключает появление другого.

Попадание
при 1 выстреле исключает промах при 1
выстреле.

1. Полная
   группа. Появится хотя бы одно из событий.

Кубик
кидают, 1 из 6.

1. Противоположные.
   Если они не совместимы и образуют
   полную группу.

Попадание
и промах.

1. Равновозможные.
   Имеют равные возможности их появления.

Как
и в полной группе.

1. Благоприятствующие.
   Исходы, при которых случайное событие
   произойдет.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Заказать задачи по любым предметам можно здесь от 10 минут

Как решать дифференциальные уравнения

Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.

Основные понятия и определения

Определения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).

Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y» = 1 $$

Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y»(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.

Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.

В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y»(x)$, поэтому это ДУ второго порядка. 

Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.

Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.

Типы уравнений

1. ДУ первого порядка
   – с разделяющимися переменными
   – однородные
   – линейные неоднородные
   – уравнение Бернулли
2. ДУ второго порядка
   – уравнения допускающие понижение порядка
   – однородные с постоянными коэффициентами
   – неоднородные с постоянными коэффициентами 

Алгоритм решения

1. По старшей производной функции $y(x)$ определить порядок ДУ
2. Зная порядок, определить тип уравнения
3. Узнав тип, подобрать подходящий метод решения
4. Используя метод, найти общее решение
5. Получить частное решение из общего путем вычисления неизвестной $C$

В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$

ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!

Пример 1

Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$

Решение

Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ.

Ответ

$$y = Ce^{frac{x^2}{2}} $$

Дифференциальные уравнения первого порядка

ДУ с разделяющимися переменными

Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$

СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.

Алгоритм нахождения общего решения:

1. Переписываем производные через $y’ = frac{dy}{dx}$
2. Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
3. Интегрируем обе части уравнения

Пример 2

Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$

Решение

Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка.  Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить «игрики» от «иксов» по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. $$ y = e^{frac{x^2}{2}} cdot e^C $$ Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$

Ответ

$$ y = Ce^{frac{x^2}{2}} $$

Пример 3

Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$.

Решение

Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y =  int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = ln(1+x^2)$$

Однородные ДУ

Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.

Решается по следующему алгоритму:

1. Проверить уравнение на однородность с помощью $lambda$
2. Привести уравнение к виду $y’ = f(frac{y}{x})$
3. Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
4. Решить уравнение методом разделяющихся переменных

Пример 4

Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} — 1$$

Решение

Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} — 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} — 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t — 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = — int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$

Ответ

$$y = -xln|x| +Cx$$

Пример 5

Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$

Решение

Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = — int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y^2 = Cxe^frac{-y}{x}$$

Линейные неоднородные ДУ

Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$

Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$. 

Алгоритм метода Бернулли:

1. Выполняем замену $y=uv$ и $y’ = u’v+uv’$
2. Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
3. Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ

Алгоритм метода вариации произвольной постоянной:

1. Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
2. В полученном общем решении заменяем константу $C$ на функцию $C(x)$
3. Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
4. Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ

Пример 6

Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$.

Решение

Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ — 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 — x^2.$$

Ответ

$$y = x^4 — x^2$$

Пример 7

Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$.

Решение

Перепишем уравнение в виде $$ y’ — y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ — y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x — C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x — cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x — cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = Csin x — cos x$$

ДУ Бернулли

Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$

Алгоритм решения: 

1. Выполняем подстановку $y = z^frac{1}{1-alpha}$
2. После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
3. Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$

Пример 8

Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$.

Решение

Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} — int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$

Ответ

$$y = frac{1}{Ce^x + x + 1}$$

ДУ в полных дифференциалах

Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.

Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:

1. Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
2. Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$ 
3. Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$

Пример 9

Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$

Решение

Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$  Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$x^2+5xy+y^3 = C.$$

Дифференциальные уравнения второго порядка

ДУ допускающие понижение порядка

Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:

1. Без функции $y$: $F(x,y’,y»)=0$
2. Без переменной $x$: $F(y,y’,y»)=0$

Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.

Пример 10

Найти частное решение дифференциального уравнения второго порядка $xy»+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$.

Решение

Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$

Ответ

$$y = ln|x|$$

Пример 11

Найти частное решение дифференциального уравнения второго порядка $$yy»+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$

Решение

Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y» = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$  Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 — Cfrac{1}{y^2}$$ $$(y’)^2 = 1 — Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 — Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 — Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$

Ответ

$$y = x + 1$$

Линейные однородные ДУ с постоянными коэффицентами

Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y»+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y» Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$

В зависимости от получившихся корней имеем общее решение в различных видах:

1. Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
2. Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
3. Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.

Пример 12

Найти общее решение дифференциального уравнения второго порядка $y»+y’-2y = 0$.

Решение

Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$y = C_1 e^{-2x} + C_2 e^{x}$$

Линейные неоднородные ДУ с постоянными коэффициентами

Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y»+py’+q = f(x).$$

Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$

Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.

№	Правая часть	Корни характеристического многочлена	Вид частного решения
1	$$P_n (x)$$	Число 0 не является корнем характеристического уравнения.	$$tilde{P_n}(x)$$
Число 0 – корень характеристического уравнения кратности $S$.	$$x^s tilde{P_n}(x)$$
2	$$P_n (x) e^{alpha x}$$	Число $alpha$ не является корнем характеристического уравнения.	$$tilde{P_n} (x) e^{alpha x}$$
Число $alpha$ является корнем характеристического уравнения кратности $S$.	$$x^s tilde{P_n} (x) e^{alpha x}$$
3	$$P_n (x) cos beta x + Q_m (x) sin beta x$$	Число $pm ibeta$ не является корнем характеристического уравнения.	$$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$
Число $pm ibeta$ является корнем характеристического уравнения кратности $S$.	$$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$
4	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$	Число $alpha pm ibeta$ не является корнем характеристического уравнения.	$$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$
Число $alpha pm ibeta$ является корнем характеристического уравнения.	$$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$

Пример 13

Найти общее решение дифференциального уравнения второго порядка $y»+y = 4xcos x$.

Решение

Сначала находим общее решение однородного уравнения $$y» + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y»_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y»_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y»_text{ч.н.}$ в исходный диффур из «дано» задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$

Ответ

$$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$

Пример 14

Найти общее решение дифференциального уравнения второго порядка $y»+y’=5x+2e^x$.

Решение

Сначала найдем общее решение однородного дифференциального уравнения $$y»+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y»=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y»$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 — 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x.$$

Ответ

$$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x$$

Метод Лагранжа

Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.

1. Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
2. Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
3. Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
4. Получаем $C_1(x)$ и $C_2(x).$

Пример 15

Найти частное решение дифференциального уравнения $$y»-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$

Решение

Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y»-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$

Ответ

$$y = xe^x(1+ln|x|)$$

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Помощь в написании работы

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь 

   

переписываем дифференциальное уравнение, получаем

   

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей  по правилу пропорции получаем

   

Далее интегрируем полученное уравнение:

   

В данном случае интегралы берём из таблицы:

   

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

То есть,

   

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

y=Cx, где С=Const.

Задание

Найти частное решение дифференциального уравнения

   

.

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

   

   

   

   

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

   

   

Если  – это константа, то

   

– тоже некоторая константа, заменим её буквой С:

   

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

   

где С=const.

Ответ

   

где С=const.

Задание

Решить дифференциальное уравнение

   

Решение

В первую очередь необходимо переписать производную в необходимом виде:

   

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

   

   

После разделения переменных, интегрируем уравнение, как в примерах выше.

   

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

   

   

   

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

   

   

   

   

Приводим полученный общий интеграл к виду: F(x,y)=C:

   

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Общий интеграл:

   

где С=const.

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

   

   

   

   

   

   

   

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

   

   

Получаем общее решение:

   

где С=const

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

   

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

.

Задание

Решить дифференциальное уравнение

   

.

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

   

   

   

   

   

В данном случае константу C считается  не обязательным определять под логарифм.

Ответ

Общий интеграл:

   

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

   

   

Интегрируем:

   

   

   

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

   

Используя

   

можно выразить функцию в явном виде.

Общее решение:

   

где С=const.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

Проверка

Необходимо проверить, выполняется ли начальное условие:

   

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

   

дифференциальному уравнению. Для этого находим производную:

   

Подставим полученное частное решение

   

и найденную производную  в исходное уравнение

   

   

   

0=0

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

   

   

Ответ

Общий интеграл:

   

Задание

Найти частное решение ДУ.

   

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

   

   

   

Интегрируем:

   

   

Общий интеграл:

   

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

   

Подставляем в общее решение

   

   

   

   

Ответ

Частный интеграл:

   

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

Левую часть интегрируем по частям:

   

   

   

В интеграле правой части проведем замену:

   

   

   

Таким образом:

   

   

(здесь дробь раскладывается методом неопределенных коэффициентов)

   

Обратная замена:

   

   

   

Ответ

Общий интеграл:

   

где С=const.

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

   

   

   

   

   

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

   

   

   

   

   

   

   

   

   

   

   

Ответ

Общее решение:

   

где С=const.