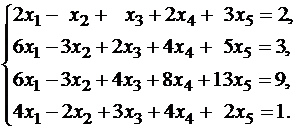Как найти частное решение однородной системы - Исправление недочетов и поиск решений вместе с Examum.ru

Как
и в общем случае исследования системы
неоднородных
линейных уравнений, использование
теоремы
Кронекера–Капелли в частном случае
исследования системы линейных однородных
уравнений также плодотворно. Общая
схема решения:

A1*:
Вычисляем
:
ранг матрицы
.
Так
как для однородной системы уравнений

=,
то всегда выполняется
.
Однородная система уравнений всегда
совместна. Пусть
=.
Это значит, что определён базовый
минор:
M
матрицы
.

A2*:
В системе уравнений оставляем только
те

уравнения-строки, которые попали
в базовый минор:
остальные являются следствием выделенных.

A3*:
В левой части каждого из оставшихся для
дальнейшего решения уравнений оставляем
те

столбцов с неизвестными, которые попали
в базовый минор:
остальные неизвестные объявляем
свободными
и соответствующие столбцы с ними
переносим в правую часть.

A4*:
Находим решения преобразованной системы
уравнений, применяя формулы Крамера:
определитель
преобразованной системы не
равен нулю!

A5*:
Полученное решение системы называют
общим:
вычисленные по формулам Крамера
неизвестные выражаются
через свободные
неизвестные. Присваивая свободным
неизвестным произвольные значения,
получаем частные
решения.

Замечание:
отметим ещё раз, что свободных неизвестных

:
их можно воспринимать как число степеней
свободы процесса; вычисляемых неизвестных
–
.

☺☺

Пример
8–04:
Исследовать систему уравнений:

Найти общее решение и одно частное.

Решение:

1). Составим матрицу:

=и найдём её ранг. Выделим для окаймления
минор (не равен нулю), расположенный в
правом верхнем углу матрицы:

	3	4	1	2
	6	8	2	5
1	9	12	3	10
	2	1

3). Окаймляющие
миноры будем обозначать:
,
где–
указывает номер отмеченной для окаймления
строки,–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:

==4·–8·+12·=m₁·(5)–h₁·(4)+g₁·(1)=4·(5)–8·(4)+12·(1)
=0;

Замечание:
параметры: m₁,
h₁,
g₁
изменяются при переходе к минорам
,,
числа:(5),
(4),
(1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!

==
m₂·(5)–h₂·(4)+g₂·(1)=
3·(5)–6·(4)+9·(1)
=0;

4).
Так как все миноры 3-го порядка
оказались равными нулю, то
=2.

5). Учитывая
расположение не равного нулю минора,
3-е уравнение отбрасываем и свободными
неизвестными объявляем
и:

далее применяем
правило Крамера:

=1; =
=;
==0.

6). Общее решение
системы:
==;
==0;
частное решение получим при значениях:=1,=–1,
→=1,=0.

Ответ:
общее решение:==;
==0;
частное решение: (1,–1,1,0).

Пример
8–05:
Исследовать
систему уравнений:

Найти
общее и частное решение.

Решение:

1). Применим пошаговый
процесс метода Гаусса:

4	-3	2	-1			1	—1	-1	2
3	-2	1	-3			1	—1	1	2
2	-1	0	-5	=(1)→	1	-1	1	2	=(2)→
5	-3	1	-8			1	0	-1	-7

1	—1	-1	2			1	0	0	-7
0	0	-2	0			0	0	1	0
0	0	-2	0	=(3)→	0	0	0	0	=(4)→
0	1	0	—9			0	1	0	—9

Выполнены
операции:
(1):
[R4]–[R1];
[R1]–[R2];
[R2]–[R3];
[R3]–[R4].
(2):
[R2]–[R1];
[R3]–[R1];
[R4]–[R1].
(3):
[R3]–[R1];
[R2]
делим на (–2); [R1]–[R2];
[R1]–[R4].
(4):

раскрываем
полученный результат.

2).
Видим:
=3.
Свободной неизвестной объявляем=.

3). Из уравнения-строки
[R4] запишем:=9;
из строки [R2]:=0;
[R4] запишем:=7.
Произвольная величинаопределяет бесчисленное множество
решений заданного уравнения.

Ответ: общее
решение: (7;9;0;)=(7,9,
0;1).

Замечание:
видим,
что и применение фундаментальных
результатов теоремы Кронекера-Капелли
не продвинуло нас в понимании системы
решений
системы ЛОУ!

☻

Соседние файлы в папке ЛА и АГ пособие

Источник

Структура общего решения системы уравнений

Однородная система линейных уравнений

$begin{cases}a_{11}x_1+a_{12}x_2+ldots+a_{1n}x_n=0,\ a_{21}x_1+a_{22}x_2+ldots+ a_{2n}x_n=0,\ cdotscdotscdotscdotscdots\ a_{m1}x_1+a_{m2}x_2+ldots+a_{mn}x_n=0,end{cases}$ или Ax=o

всегда совместна, так как имеет тривиальное решение x_1=x_2=ldots=x_n=0~(x=o) . Если ранг матрицы системы равен количеству неизвестных (operatorname{rg}A=n) , то тривиальное решение единственное. Предположим, что r=operatorname{rg}A<n . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица (Amid o) однородной системы при элементарных преобразованиях строк приводится к упрощенному виду (A'mid o) , т.е. b'_1=b'_2=ldots=b'_r=0 . Поэтому из (5.11) получаем общее решение однородной системы уравнений:

$begin{cases}x_1=-a'_{1,r+1}x_{r+1}-ldots-a'_{1n}x_n,\phantom{ x_1=-a'_{1,r+1}}vdots\ x_r=-a'_{r,r+1}x_{r+1}-ldots-a'_{rn}x_n.end{cases}$

(5.13)

Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.

Свойства решений однородной системы уравнений

1. Если столбцы varphi_1,varphi_2,ldots,varphi_k — решения однородной системы уравнений, то любая их линейная комбинация alpha_1varphi_1+alpha_2varphi_2+ ldots+alpha_kvarphi_k также является решением однородной системы.

В самом деле, из равенств Avarphi_1=o,~ Avarphi_2=o,~ldots,~ Avarphi_k=o следует, что

$Acdot! begin{pmatrix}alpha_1cdotvarphi_1+ alpha_2cdotvarphi_2+ ldots+alpha_kcdotvarphi_k end{pmatrix}= alpha_1cdot Acdotvarphi_1+ alpha_2cdot Acdotvarphi_2+ ldots+alpha_kcdot Acdotvarphi_k=o,$

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет (n-r) линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем (n-r) частных решений $varphi_1,varphi_2,ldots,varphi_{n-r}$ , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

$begin{aligned} mathsf{1)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=0colon~~ varphi_1= begin{pmatrix}-a'_{1,r+1}&cdots&-a'_{r,r+1}&1&0&cdots&0end{pmatrix}^T;\[5pt] mathsf{2)}&quad x_{r+1}=0,~x_{r+2}=1,~ldots,~x_n=0colon~~ varphi_2= begin{pmatrix}-a'_{1,r+2}&cdots&-a'_{r,r+2}&0&1&cdots&0end{pmatrix}^T;\[5pt] mathsf{n-r)}&quad x_{r+1}=1,~x_{r+2}=0,~ldots,~x_n=1colon~~ varphi_{n-r}= begin{pmatrix}-a'_{1n}&cdots&-a'_{rn}&0&0&cdots&1end{pmatrix}^T. end{aligned}$

Получим (n-r) решений

$varphi_1= begin{pmatrix}-a'_{1,r+1}\vdots\-a'_{r,r+1}\1\0\vdots\0end{pmatrix}!,quad varphi_2= begin{pmatrix}-a'_{1,r+2}\vdots\-a'_{r,r+2}\0\1\vdots\0end{pmatrix}!,quad ldots,quad varphi_{n-r}= begin{pmatrix}-a'_{1n}\vdots\-a'_{rn}\0\0\vdots\1end{pmatrix}!.$

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние (n-r) ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних (n-r) строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен (n-r) . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность (n-r) линейно независимых решений $varphi_1,varphi_2,ldots,varphi_{n-r}$ однородной системы называется фундаментальной системой (совокупностью) решений.

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества (n-r) линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если $varphi_1,varphi_2,ldots,varphi_{n-r}$ — фундаментальная система решений однородной системы уравнений (5.4), то столбец

$x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}$

(5.14)

при любых значениях произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных $C_{1},C_{2},ldots,C_{n-r}$ , при которых это решение удовлетворяет равенству (5.14).

Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец

$H=begin{pmatrix}varphi_1&cdots&varphi_{n-r}&xend{pmatrix}= begin{pmatrix}varphi_{11}&cdots&varphi_{1,n-r}&x_1\ vdots&ddots&vdots&vdots\ varphi_{r1}&cdots&varphi_{r,n-r}&x_r\ varphi_{r+11}&cdots&varphi_{r+1,n-r}&x_{r+1}\ vdots&ddots&vdots&vdots\ varphi_{n1}&cdots&varphi_{n,n-r}&x_n end{pmatrix}!.$

Найдем ранг этой матрицы. Так как первые (n-r) столбцов линейно независимы, то operatorname{rg}Hgeqslant n-r . Так как каждый из столбцов матрицы является решением системы A'x=o , то по первой формуле из (5.13) получаем

$begin{aligned} varphi_{11}&= -a'_{1,r+1}varphi_{r+11}-ldots- a'_{1n}varphi_{n1},\ cdots & cdotscdotscdotscdots\[2pt] varphi_{1,n-r}&= -a'_{1,r+1}varphi_{r+1,n-r}-ldots- a'_{1n}varphi_{n,n-r},\[2pt] x_1&= -a'_{1,r+1}x_{r+1}-ldots- a'_{1n}x_n. end{aligned}$

Следовательно, первая строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних (n-r) строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, operatorname{rg}Hleqslant n-r , так как после вычеркивания в матрице будет всего (n-r) строк. Таким образом, operatorname{rg}H=n-r . Значит, есть базисный минор матрицы , который расположен в первых (n-r) ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа $C_1,C_2,ldots,C_{n-r}$ , что

$x=C_1cdotvarphi_1+C_2cdotvarphi_2+ldots+C_{n-r}cdotvarphi_{n-r}.$

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).

Если ранг матрицы системы равен числу неизвестных (r=operatorname{rg}A=n) , то система имеет единственное тривиальное решение x-o и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных (operatorname{rg}A<n) , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему $varphi_1, varphi_2, ldots,varphi_{n-r}$ решений однородной системы. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

Замечания 5.3

1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.

2. Матрица $Phi=begin{pmatrix}varphi_1&varphi_2&cdots&varphi_{n-r} end{pmatrix}$ столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

x=Phicdot c , где $c=begin{pmatrix}C_1&cdots&C_{n-r} end{pmatrix}^T$ — столбец произвольных постоянных.

3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы

$begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&0\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&0\ 0&0&cdots&0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix} E_r!!&vline!!&A'_{rtimes(n-r)}!!&vline!!&o\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Тогда блочная матрица $Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}$ размеров ntimes(n-r) является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

$begin{cases}x_1+x_2+2x_3+x_4=0,\[2pt] 2x_1+3x_2+x_4=0,\[2pt] 3x_1+4x_2+2x_3+2x_4=0. end{cases}$

Решение. 1. Составляем расширенную матрицу системы

$begin{pmatrix}Amid oend{pmatrix}= begin{pmatrix} 1&1&2&1!!&vline!!&0\ 2&3&0&1!!&vline!!&0\ 3&4&2&2!!&vline!!&0 end{pmatrix}!.$

2-4. Используя элементарные преобразования над строками матрицы (Amid o) , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

$begin{pmatrix}A'mid oend{pmatrix}= begin{pmatrix} 1&0&6&2!!&vline!!&0\ 0&1&-4&-1!!&vline!!&0\ 0&0&0&0!!&vline!!&0 end{pmatrix}!.$

Пункт 3 метода Гаусса пропускаем.

5. Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные. Записываем формулу (5.13) общего решения однородной системы

$begin{cases}x_1=-6x_3-2x_4,\x_2=4x_3+x_4.end{cases}$

6. Находим фундаментальную систему решений. Так как n=4 и r=operatorname{rg}A=2 , надо подобрать n-r=2 линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

1) если x_3=1,~x_4=0 , то x_1=-6,~x_2=4 ;

2) если x_3=0,~x_4=1 , то x_1=-2,~x_2=1 .

В результате получили фундаментальную систему решений

$varphi_1=begin{pmatrix}-6\4\1\0end{pmatrix}!,qquad varphi_2=begin{pmatrix}-2\1\0\1end{pmatrix}!.$

7. Записываем общее решение однородной системы по формуле (5.14):

$x=C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot!begin{pmatrix}-2\1\0\1end{pmatrix}!.$

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, x_3=1,~x_4=2 и x_3=2,~x_4=3 . Тогда получим другую фундаментальную систему решений

$varphi_1=begin{pmatrix}-10\6\1\2end{pmatrix}!,quad varphi_2=begin{pmatrix}-18\11\2\3end{pmatrix}$ и общее решение системы $x=C_1cdot! begin{pmatrix}-10\6\1\2end{pmatrix}+ C_2cdot! begin{pmatrix}-18\11\2\3end{pmatrix}!.$

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему Ax=b и соответствующую ей однородную систему Ax=o . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств Ax=b и Ay=b следует, что A(x-y)=Ax-Ay=b-b=o .

2. Пусть x^H — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

x=x^H+x^O , где x^O — решение однородной системы.

В самом деле, для любого решения неоднородной системы разность x-x^H по свойству 1 является решением однородной системы, т.е. x^O=x-x^H — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть x^H — решение неоднородной системы, а $varphi_1,varphi_2,ldots,varphi_{n-r}$ — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

$x=x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2+ldots+ C_{n-r}cdotvarphi_{n-r}$

(5.15)

при любых значениях [i]произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных $C_1,C_2,ldots,C_{n-r}$ , при которых это решение удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение x^H неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему $varphi_1,varphi_2,ldots,varphi_{n-r}$ ее решений. Для этого подставить в (5.13) последовательно (n-r) стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

Замечания 5.4

1. Используя фундаментальную матрицу Phi однородной системы Ax=o , решение неоднородной системы Ax=b можно представить в виде

x=x^H+Phicdot c,

где x^H — частное решение неоднородной системы, а $c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T$ — столбец произвольных постоянных.

2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

$begin{pmatrix}A'mid b'end{pmatrix}= begin{pmatrix} 1&0&cdots&0&a'_{1,r+1}&cdots&a'_{1n}!!&vline!!&b'_1\ 0&1&cdots&0&a'_{2,r+1}&cdots&a'_{2n}!!&vline!!&b'_2\ vdots&vdots&ddots&vdots&vdots&ddots&vdots!!&vline!!&vdots\ 0&0&cdots&1&a'_{r,r+1}&cdots&a'_{rn}!!&vline!!&b'_r\ 0&0&cdots& 0&0&cdots&0!!&vline!!&0\ vdots&vdots&ddots&vdots& vdots&ddots& vdots!!&vline!!&vdots\ 0&0&cdots&0&0&cdots&0!!&vline!!&0 end{pmatrix}= begin{pmatrix}E_r!!& vline!!&A'_{rtimes(n-r)}!!&vline!!&b'_{rtimes1}\hline O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Тогда блочная матрица $Phi=begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}$ оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец $x^H=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}$ является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

$x=x^H+Phicdot c=begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}+begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}!cdot c,$

(5.16)

где $c=begin{pmatrix}C_1&cdots&C_{n-r}end{pmatrix}^T$ — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

$begin{cases}x_1+ x_2+2x_3+x_4=1,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=1.end{cases}$

Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

$begin{cases}x_1=3-6x_3-2x_4,\x_2=-2+4x_3+x_4.end{cases}$

Переменные x_1,,x_2 — базисные, а x_3,,x_4 — свободные.

6. Полагая x_3=0,~x_4=0 , получаем частное решение неоднородной системы $x^H=begin{pmatrix}3&-2&0&0end{pmatrix}^T$ .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

$varphi_1=begin{pmatrix}-6&4&1&0end{pmatrix}^T,qquad varphi_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T.$

8. Записываем по формуле (5.15) общее решение неоднородной системы

$x=x^H+C_1cdotvarphi_1+C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.$

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

$begin{pmatrix}Amid bend{pmatrix}= begin{pmatrix}1&0&6&2!!&vline!!&3\ 0&1&-4&-1!!&vline!!&-2\ 0&0&0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} 1&0!!& vline!!&6&2!!&vline!!&3\ 0&1!!&vline!!&-4&-1!!&vline!!&-2\hline 0&0!!&vline!!& 0&0!!&vline!!&0end{pmatrix}= begin{pmatrix} E_2!!&vline!!&A'_{2times2}!!& vline!!& b'_{2times1}\ O!!&vline!!&O!!&vline!!&o end{pmatrix}!.$

Записываем частное решение неоднородной системы

$x^H= begin{pmatrix}dfrac{b'_{rtimes1}}{o_{(n-r)times1}}end{pmatrix}= begin{pmatrix}dfrac{b'_{2times1}}{o_{2times1}}end{pmatrix}= begin{pmatrix}3\-2\0\0 end{pmatrix}$

и составляем фундаментальную матрицу:

$Phi= begin{pmatrix}dfrac{-A'_{rtimes(n-r)}}{E_{n-r}}end{pmatrix}= begin{pmatrix}dfrac{-A'_{2times2}}{E_2}end{pmatrix}= begin{pmatrix}-6&-2\4&1\1&0\ 0&1end{pmatrix}= begin{pmatrix}varphi_1&varphi_2end{pmatrix}!.$

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

$x=x^H+Phicdot! begin{pmatrix}C_1\C_2end{pmatrix}= x^H+C_1cdotvarphi_1+ C_2cdotvarphi_2= begin{pmatrix}3\-2\0\0end{pmatrix}+ C_1cdot! begin{pmatrix}-6\4\1\0 end{pmatrix}+ C_2cdot! begin{pmatrix}-2\1\0\1end{pmatrix}!.$

которое совпадает с ранее полученным.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Как найти общее и частное решение системы линейных уравнений

Пример 2. Исследовать совместность, найти общее и одно частное решение системы

Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.

Получим нули в четвертом столбце, оперируя первой строкой:

Теперь получим нули в третьем столбце с помощью второй строки:

Третья и четвертая строки пропорциональны, поэтому одну из них можно вычеркнуть, не меняя ранга:
Третью строку умножим на (–2) и прибавим к четвертой:

Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x₁=-3 → x₁=3; x₂=3-x₁ → x₂=0; x₃=1-2x₁ → x₃=5.
x₄ = 10- 3x₁ – 3x₂ – 2x₃ = 11.

Пример 3. Исследовать систему на совместность и найти решение, если оно существует.

Решение. Составляем расширенную матрицу системы.

Переставляем первые два уравнения, чтобы в левом верхнем углу была 1:
Умножая первую строку на (-1), складываем ее с третьей:

Умножим вторую строку на (-2) и прибавим к третьей:

Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть r_B > r_A.

Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение

Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.

Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x₃ = — 1 + x₄ + x₅; x₂ = 1 — x₄; x₁ = 2 + x₄ — 3x₅

Задание. Найти общее и частное решения каждой системы.
Решение. Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:

1	1	14	0	2	0
3	4	2	3	0	1
2	3	-3	3	-2	1
x₁	x₂	x₃	x₄	x₅

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	-1	40	-3	6	-1
3	4	2	3	0	1
2	3	-3	3	-2	1

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:

0	-1	40	-3	6	-1
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0	0	27	0	0	0
0	-1	13	-3	6	-1
2	3	-3	3	-2	1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂,x₃, значит, неизвестные x₁,x₂,x₃ – зависимые (базисные), а x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	0	27	0	0	0
0	-1	13	-1	3	-6
2	3	-3	1	-3	2
x₁	x₂	x₃	x₄	x₅

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x₃ =
— x₂ + 13x₃ = — 1 + 3x₄ — 6x₅
2x₁ + 3x₂ — 3x₃ = 1 — 3x₄ + 2x₅
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x₁,x₂,x₃ через свободные x₄,x₅, то есть нашли общее решение:
x₃ = 0
x₂ = 1 — 3x₄ + 6x₅
x₁ = — 1 + 3x₄ — 8x₅
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

Задание. Решить систему уравнений.
Ответ ₂ = 2 — 1.67x₃ + 0.67x₄
x₁ = 5 — 3.67x₃ + 0.67x₄
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной

Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера — Капелли. Согласно теореме Кронекера — Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение

Структура общего решения системы уравнений

Однородная система линейных уравнений

всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :

Свойства решений однородной системы уравнений

1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.

Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец

при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).

Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем

Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.

По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что

Итак, обратное утверждение доказано.

Алгоритм решения однородной системы уравнений

Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.

Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.

6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).

7. Записать общее решение однородной системы по формуле (5.14).

2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде

Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.

Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы

Решение. 1. Составляем расширенную матрицу системы

2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):

Пункт 3 метода Гаусса пропускаем.

5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы

6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:

В результате получили фундаментальную систему решений

7. Записываем общее решение однородной системы по формуле (5.14):

Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений

Несмотря на различия, обе формулы задают одно и то же множество решений.

Структура общего решения неоднородной системы уравнений

Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений и неоднородной системы есть решение однородной системы.

Действительно, из равенств и следует, что .

2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде

В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде

Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

Переменные — базисные, а — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

Основные определения и понятия

Рассмотрим систему m уравнений с n неизвестными

. (1)

Матрица A,составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1)

называют расширенной матрицей системы, ее последний столбец отделяют вертикальной чертой.

и .

называют соответственно вектором неизвестных и вектором правых частей системы (1). В этих обозначениях векторно-матричная запись системы (1) выглядит так:

(2)

Если вектор , то система называется однородной, если же (хотя бы один из элементов отличен от нуля), то система называется неоднородной.

Решением системы (1) называется такой вектор , что при подстановке чисел в систему (1) получаются верные равенства (тождества).

Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.

Две системы называются эквивалентными, если множества их решений совпадают. Если к некоторому уравнению системы прибавить другое, умноженное на число, то решения системы не меняются. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей . Таким образом, элементарные преобразования над не меняют совокупности ее решений.

Однородные системы

Рассмотрим однородную систему

(3)

Заметим, что однородная система всегда совместна, поскольку нуль-вектор – ее решение.

Вопрос лишь в том, единственно ли это решение и если нет, то что представляет собой совокупность всех ее решений.

Теорема. Множество всех решений однородной системы образует подпространство в

Действительно, если – решения системы (3), т.е. и , то , где – числа, также является решением системы (3):

Итак, решения однородной системы можно складывать, умножать на число, новый вектор вновь будет решением этой системы. Мы знаем, что в любом подпространстве (кроме ) можно выделить базис и любой вектор подпространства представить в виде линейной комбинации векторов базиса.

Обозначим V – подпространство решений однородной системы (3), а – некоторый базис в V.

Любой базис подпространства V решений однородной системы называют фундаментальной системой решений (ФСР).

Число векторов ФСР , где – число неизвестных системы (3), а r – ранг матрицы A. Таким образом, размерность подпространства решений .

Любой вектор-решение (общее решение) является линейной комбинацией векторов ФСР: .

Научимся находить общее решение однородной системы. Для этого применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе, которая легко поддается исследованию. Решение системы находится обратным ходом метода Гаусса.

Проиллюстрируем алгоритм метода на примере системы:

Все преобразования системы сводятся к преобразованиям матрицы системы.

Прямой ход метода Гаусса.

1. Приведем матрицы системы к ступенчатому виду:

Матрица ступенчатая, ее ранг .

2. Выпишем соответствующую систему уравнений:

Мы отбросили последнее уравнение, все коэффициенты которого равны нулю. Заметим, что угловые элементы матрицы являются коэффициентами при в ступенчатой системе.

3. Назовем переменные , не связанные с угловыми элементами, свободными, а – зависимыми переменными (несвободными). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно
В данном примере

Обратный ход метода Гаусса.

1. Выразим зависимые переменные через свободные из ступенчатой системы, начиная с последнего уравнения и «поднимаясь» вверх к первому. В результате получим

. (*)

Полученные выражения дают описание всего множества решений однородной системы (3). Давая свободным переменным произвольные значения (они играют роль параметров для множества решений) и вычисляя значения зависимых переменных, получаем некоторое частное решение системы. Так можно получить все решения системы, поэтому выражения (*) называют общим решением системы в координатной форме.

2. Запишем общее решение в векторной форме. Выберем из общего решения (*) линейно независимых решений и составим из них ФСР. Для этого придадим свободным переменным значения , тогда из (*) получим и ; затем , вычислим из (*) и .

Векторы линейно независимы (в силу выбора свободных переменных) и образуют ФСР.

Общее решение системы, записанное в векторной форме, имеет вид

Итак, размерность подпространства есть , где . Если (т.е. A имеет «полный ранг»), , т.е. имеет нулевую размерность ( ), а значит, состоит лишь из нулевого вектора . В этом случае однородная система имеет единственное нулевое (тривиальное) решение.

Неоднородные системы

Мы научились находить общее решение однородной системы. Перейдем теперь к неоднородным системам. Процедура получения общего решения (в координатной и векторной формах) для них будет похожей.

Пусть дана система или в координатной форме

Соответствующая этой системе однородная система имеет ту же матрицу системы , а вектор правых частей , т.е. .

Справедливо следующее утверждение.

Пусть – некоторое частное решение неоднородной системы , а – решение соответствующей однородной системы. Тогда вектор будет решением неоднородной системы. Действительно, .

Это означает, что к решениям однородной системы можно прибавить решение неоднородной системы, в результате получим решение неоднородной системы.

Чтобы получить общее решение неоднородной системы, нужно к общему решению соответствующей однородной системы прибавить некоторое частное решениенеоднородной.

В отличие от однородной системы неоднородная не всегда совместна, поэтому прежде чем находить решение системы необходимо выяснить вопрос, существует ли хотя бы одно решение, т.е. совместна ли система. Ответ на этот вопрос дает теорема Кронекера-Капелли (критерий совместности неоднородной системы): система совместна тогда и только тогда, когда ранг основной матрицы A равен рангу расширенной матрицы .

Рассмотрим метод Гаусса для решения неоднородной системы уравнений на примере системы

Прямой ход метода Гаусса.

1. Приведем расширенную матрицу системы к ступенчатому виду

Здесь , система совместна.

2. Запишем эквивалентную ступенчатую систему:

Переменные являются зависимыми, а – свободной переменной.

Обратный ход метода Гаусса.

1. Выразим зависимые переменные через свободные. Запишем общее решение неоднородной системы в координатной форме.

Выразим переменные через свободную переменную :

(*)

Полученные равенства задают общее решение исходной системы в координатной форме. Заметим, что для получения общего решения однородной системы нет нужды повторять заново всю процедуру. Достаточно в формулах (*) заменить свободные члены нулями. Получим общее решение однородной системы в координатной форме:

(**)

Размерность подпространства V решений однородной системы , а значит, ФСР содержит лишь один вектор. Найдем его из равенств (**), придавая свободной переменной любое отличное от нуля значение, например, пусть , тогда , , и базисный вектор .

Общее решение однородной системы в векторной форме выглядит так: , здесь – произвольная постоянная (сокращение «оо» означает общее «однородного»).

Остается найти частное решение неоднородной системы. Для этого в формулах (*) свободной переменной придадим произвольное (например, нулевое) значение, получаем: .

– общее решение в векторной форме.

Пример.

, ; ;

Таким образом, ранги расширенной и основной матриц системы не равны, теорема Кронекера-Капелли не выполняется, система несовместна. Итак, всякое решение неоднородной системы ( – «общее неоднородной») есть сумма частного решения неоднородной ( ) и общего решения однородной ( ): , или , где – фундаментальная система решений (базис подпространства решений однородной системы). Можно показать, что множество решений неоднородной системы не является подпространством (проверьте это самостоятельно). Множество представляет собой сдвиг пространства V на произвольный вектор . Результат сдвига не зависит от выбора частного решения .

Говорят, что множество является «параллельным сдвигом» подпространства V. Понимать это нужно так: любой вектор – решение неоднородной системы может быть получен по формуле соответствующим подбором постоянных .

источники:

http://mathhelpplanet.com/static.php?p=struktura-obshchego-resheniya-sistemy-uravnenii

http://allrefrs.ru/5-34003.html

Источник

Содержание:

Однородные СЛАУ
Фундаментальная система решений

Однородные СЛАУ

Определение

Однородной СЛАУ называется система, все правые части которой равны нулю одновременно.

Однородная СЛАУ, записанная в
матричном виде, $A X=Theta$ всегда совместна,
так как $X=Theta$ всегда является ее решением.

Заметим, что если $x_{1}, x_{2}$ — это два решения однородной
СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:

$$Y=lambda_{1} x_{1}+lambda_{2} x_{2}$$
$$A Y=Aleft(lambda_{1} x_{1}+lambda_{2} x_{2}right)=lambda_{1} A x_{1}+lambda_{2} A x_{2}=lambda_{1} Theta+lambda_{2} Theta=Theta$$

Теорема

Если однородная квадратная СЛАУ имеет ненулевое решение, то
определитель матрицы системы равен нулю.

Пример

Задание. Выяснить, имеет ли однородная СЛАУ
$left{begin{array}{l}
3 x-2 y=-1 \
x+3 y=7
end{array}right.$ ненулевые решения.

Решение. Вычислим определитель матрицы системы:

$$Delta=left|begin{array}{rr}
3 & -2 \
1 & 3
end{array}right|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Фундаментальная система решений

Рассмотрим множество всех столбцов, которые являются решениями исходной системы.

Определение

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы.
Любое решение исходной системы есть линейная комбинация решений ФСР.

Теорема

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и
общего решения соответствующей однородной СЛАУ.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти общее решение и ФСР однородной системы
$left{begin{array}{l}
x_{1}+x_{2}-3 x_{4}-x_{5}=0 \
x_{1}-x_{2}+2 x_{3}-x_{4}=0 \
4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \
2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0
end{array}right.$

Решение. Приведем систему к ступенчатому виду с помощью
метода Гаусса. Для этого записываем
матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец
свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут
получаться нули):

$$A=left(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
1 & -2 & 2 & -1 & 0 \
4 & -2 & 6 & 3 & -4 \
2 & 4 & -2 & 4 & -7
end{array}right)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей — четыре первых, от четвертой — две первых:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & -6 & 6 & 15 & 0 \
0 & 2 & -2 & 10 & -5
end{array}right)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три
вторых, к четвертой прибавляем вторую:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 9 & -3 \
0 & 0 & 0 & 12 & -4
end{array}right)$$

От четвертой строки отнимем $frac{4}{3}$ третьей и третью
строку умножим на $frac{1}{3}$ :

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1 \
0 & 0 & 0 & 0 & 0
end{array}right)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -3 & -1 \
0 & -2 & 2 & 2 & 1 \
0 & 0 & 0 & 3 & -1
end{array}right)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а
ко второй строке прибавляем третью:

$$A simleft(begin{array}{rrrrr}
1 & 1 & 0 & -6 & 0 \
0 & -2 & 2 & 5 & 0 \
0 & 0 & 0 & 3 & -1
end{array}right)$$

то есть получаем систему, соответствующую данной матрице:

$$left{begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \
-2 x_{2}+2 x_{3}+5 x_{4}=0 \
3 x_{4}-x_{5}=0
end{array}right.$$

Или, выразив одни переменные через другие, будем иметь:

$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{2}=x_{2} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{4}=x_{4} \
x_{5}=3 x_{4}
end{array}right.$$

Здесь $x_{2}, x_{4}$ — независимые (или свободные)
переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ — зависимые (связанные) переменные
(то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от
пяти переменных) и ранга матрицы $r$ (в этом
случае получили, что $r=3$ — количество
ненулевых строк после приведения матрицы к ступенчатому виду):
$n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР
$n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).

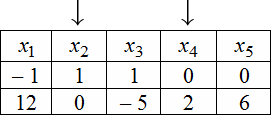
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть
для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки).
В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным
придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными
находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

$$left{begin{array}{l}
x_{1}=-x_{2}+6 x_{4} \
x_{3}=x_{2}-frac{5}{2} x_{4} \
x_{5}=3 x_{4}
end{array}right.$$

Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что $left{begin{array}{l}
x_{1}=-1+6 cdot 0=-1 \
x_{3}=1-frac{5}{2} cdot 0=1 \
x_{5}=3 cdot 0=0
end{array}right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
{x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

$$X_{1}=left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right), X_{2}=left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$

Общее решение является линейной комбинацией частных решений:

$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}left(begin{array}{r}
-1 \
1 \
1 \
0 \
0
end{array}right)+C_{2}left(begin{array}{r}
12 \
0 \
-5 \
2 \
6
end{array}right)$$

где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:

$left{begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \
x_{2}=C_{1} \
x_{3}=C_{1}-5 C_{2} \
x_{4}=2 C_{2} \
x_{5}=6 C_{2}
end{array}right.$
$C_{1}, C_{2} neq 0$

Придавая константам $C_{1}, C_{2}$ определенные значения
и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Читать дальше: примеры решения СЛАУ.

Источник

Найти решение системы дифференциальных уравнений

СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ

Основные понятия
Метод исключения
1. Пример 1
2. Пример 2
3. Пример 3
Метод Эйлера
1. Пример 4

Основные понятия

В данной статье рассмотрим линейные системы дифференциальные уравнений, которые делятся на два вида: однородные и неоднородные. В общем виде они записываются следующим образом $$begin{cases} frac{dx}{dt} = a_1 x(t) + b_1 y(t) + f_1(t) \ frac{dy}{dt} = a_2 x(t) + b_2 y(t) + f_2(t) end{cases},$$где $a_1, b_1, c_1, a_2$ коэффициенты, функции $f_1(t)$ и $f_2(t)$ могут отсутствовать, либо быть константами, $x(t),y(t)$ неизвестные функции, которые требуется найти в качестве решения системы ДУ. Напоминаем, что аналогичная запись $frac{dx}{dt} = x'(t)$ и $frac{dy}{dt} = y'(t)$.

Если хотя бы один из коэффициентов $f_1(t)$ или $f_2(t)$ не равен нулю, то система называется неоднородной. Если $f_1(t) = f_2(t) = 0$, то система однородная.

Решением системы дифференциальных уравнений называется пара функций $y(t), x(t)$, подстановка которых в систему обращает её в тождество.

Разберём два основных способа решения линейных систем дифференциальных уравнений: метод исключения и метод Эйлера.

Метод исключения

Суть метода в том, что два уравнения сводятся к одному линейному дифференциальному уравнению. Для этого есть примерный алгоритм:

Находим производную одного из уравнений системы, например, $y»_t$
В получившейся производной исключаем всё что связано с $x$
Решаем линейное дифференциальное уравнение относительно $y(t)$
Подставляем получившийся $y(t)$ в одно из уравнений системы, чтобы найти $x(t)$

Пример 1

Решить систему дифференциальных уравнений методом исключения $$begin{cases} frac{dx}{dt} =y-7 \ frac{dy}{dt} = -2x — 3y end{cases}.$$

Решение

Применим метод исключения, чтобы из двух уравнений получить одно. Берем первое уравнение и дифференцируем его по $t$. $$frac{d^2 x}{dt^2} = frac{dy}{dt}$$ В получившееся уравнения вместо $frac{dy}{dt}$ подставим второе уравнение системы. $$frac{d^2 x}{dt^2} = -2x — 3y$$ Теперь нужно избавиться от $y$, чтобы остались только $x$, и тогда можно будет решить дифференциальное уравнение относительно $x(t)$. Для этого берём первое уравнение системы и получаем из него $$y = frac{dx}{dt}+7.$$ Продолжаем решение с учётом полученного $y$ $$frac{d^2 x}{dt^2} = -2x — 3 (frac{dx}{dt}+7).$$ После раскрытия скобок и преобразований получаем уравнение $$frac{d^2 x}{dt^2} + 3frac{dx}{dt} + 2x = 21.$$ Это линейное неоднородное дифференциальное уравнение второго порядка. Решение его будем искать в виде $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$.

Сначала находим общее решение однородного уравнения $x_text{о.о.}$. Для этого отбрасываем правую часть уравнения и составляем характеристический многочлен и находим его корни. $$lambda^2 + 3lambda + 2 = 0,$$ $$lambda_{1,2} = frac{-3pm sqrt{9-4cdot 1 cdot 2}}{2} = frac{-3pm 1}{2},$$ $$lambda_1 = -1, lambda_2 = -2.$$ Итак, записываем $$x_text{о.о.} = C_1 e^{-t} + C_2 e^{-2t}.$$

Искать частное решение $x_text{ч.н.}$ будем искать методом подбора правой части исходного неоднородного линейного дифференциального уравнения. В данном случае в правой части стоит константа, значит подбор будет в виде $x_text{ч.н.} = A$. Находим первую и вторую производную и подставляем в исходное решаемое уравнение. $$x’_text{ч.н.} = 0, x»_text{ч.н.} = 0$$ $$0 + 3 cdot 0 + 2 A = 21 Rightarrow A = frac{21}{2}.$$ Значит, $x_text{ч.н.} = frac{21}{2}$.

Записываем окончательно, что $$x(t) = x_text{о.н.} = x_text{о.о.} + x_text{ч.н.} = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2}$$

Теперь зная $x(t)$ можно получить $y(t)$. Для этого нужно вернуться к началу решения и вспомнить, что мы выражали $y = frac{dx}{dt}+7$. Таким образом осталось в него подставить полученное решение $x(t)$ $$y(t) = (C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2})’ + 7 = -C_1 e^{-t} — 2C_2 e^{-2t} + 7$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$begin{cases} x(t) = C_1 e^{-t} + C_2 e^{-2t} + frac{21}{2} \ y(t) = -C_1 e^{-t} — 2C_2 e^{-2t} + 7 end{cases}$$

Пример 2

Найти решение системы дифференциальных уравнений $$begin{cases} x’ = -2y+3t \ y’ = 2x+4 end{cases},$$ где $x(t),y(t)$ — искомые функции, $t$ — независимая переменная.

Решение

Решаем методом исключения, то есть два уравнения приводим к одному. Берем производную первого уравнения по $t$. $$x» = (-2y+3t)’_t = -2y’+3$$ Знаем чему равен $y’$ из второго уравнения системы и поэтому его подставляем в получившееся последнее уравнение. $$x» = -2(2x+4)+3 = -4x — 8 + 3 = -4x — 5$$

Переписываем последнее получившееся уравнение в форме линейного неоднородного дифференциального уравнения второго порядка. $$x» + 4x = -5$$

Общее решение этого уравнения найдем в качестве суммы общего решения однородного уравнения и частного решения неоднородного $x_text{о.н.} = x_text{о.о.} + x_text{ч.н.}$. Итак, составляем характеристический многочлен и находим его корни. $$lambda^2 + 4 = 0$$ $$lambda_1 = -2i, lambda_2 = 2i.$$ Так как получились комплексные корни, то общее решение записывается следующим образом $$x_text{о.о.} = C_1cos 2t + C_2 sin 2t.$$ Осталось найти $x_text{ч.н.}$. Для этого воспользуемся методом подбора правой части. Так как она представляет собой константу, то значит $x_text{ч.н.} = A$. Отсюда следует, что $x»_text{ч.н.} = 0$. Подставляя эти данные в дифференциальное уравнение получаем значение $A$. $$0 + 4A = -5,$$ $$A = -frac{5}{4}.$$

Таким образом можно записать, что $$x(t) = x_text{о.о.} + x_text{ч.н.} = C_1cos 2t + C_2 sin 2t -frac{5}{4}.$$

Осталось найти функцию $y(t)$. Для этого выразим её из первого уравнения и подставим ранее полученный $x(t)$. $$y = frac{3}{2}t — frac{x’}{2},$$ $$y = frac{3}{2}t — frac{1}{2}(C_1cos 2t + C_2 sin 2t -frac{5}{4})’ = $$ $$ = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t.$$

Ответ

$$begin{cases} x(t) = C_1cos 2t + C_2 sin 2t -frac{5}{4} \ y(t) = frac{3t}{2} + C_1 sin 2t — C_2 cos 2t end{cases}$$

Пример 3

Найти общее и частное решение системы дифференциальных уравнений $$begin{cases} frac{dx}{dt} = 2x+y \ frac{dy}{dt} = x+2y end{cases}, x(0)=1, y(0)=3$$

Решение

Берем второе уравнение и находим его производную по $t$. $$frac{dy^2}{dt^2} = frac{dx}{dt}+2frac{dy}{dt}$$ В полученное равенство вместо frac{dx}{dt} подставим первое уравнение системы. $$frac{dy^2}{dt^2} = 2x+y + 2frac{dy}{dt}$$ Осталось избавиться от $x$. Для этого выразим его из второго уравнения системы и подставим в последнее полученное уравнение. $$frac{dy^2}{dt^2} = 2(frac{dy}{dt} — 2y) + y + 2frac{dy}{dt}$$ Раскроем скобки и перенесем всё в левую сторону. Затем запишем для удобства $frac{dy}{dt} = y’$. $$y» — 4y’ + 3y = 0$$

Получившееся дифференциальное уравнение называется однородным линейным ду второго порядка. Для его решения составляем характеристический многочлен и находим его корни. $$lambda^2 — 4lambda + 3 = 0,$$ $$lambda_{1,2} = frac{4pm sqrt{16 — 4 cdot 1 cdot 3}}{2} = frac{4pm 2}{2},$$ $$lambda_1 = 1, lambda_2 = 3.$$ Общее решение такого уравнения записывается в виде $$y = C_1 e^{3t} + C_2e^{t}.$$

Так как мы нашли $y(t)$, то теперь можем найти $x(t)$. Для этого подставляем $y(t)$ во второе уравнение системы и выражаем $x(t)$. $$x(t) = frac{dy}{dt} — 2y = (C_1 e^{3t} + C_2e^{t})’ — 2(C_1 e^{3t} + C_2e^{t})$$ После раскрытия скобок и упрощения остаётся $$x(t) = 3C_1 e^{3t} + C_2 e^t — 2C_1 e^{3t} — 2C_2 e^t = C_1 e^{3t} — C_2 e^t.$$ Вот таким образом находится общее решение системы дифференциальных уравнений $$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}.$$

По условию задания необходимо кроме общего найти частное решение. Для этого берем дополнительные условия из задачи $x(0)=1, y(0)=3$ и подставляем в полученное общее решение, чтобы вычислить константы $C_1$ и $C_2$. $$begin{cases} x(0) = C_1e^{0}-C_2e^0 = 1 \ y(0) = C_1 e^0 + C_2 e^0 = 3 end{cases},$$ $$ begin{cases} C_1-C_2 = 1 \ C_1 + C_2 = 3 end{cases} Rightarrow begin{cases} C_1 = 2 \ C_2 = 1 end{cases}.$$ Теперь зная постоянные можно записать частное решение системы дифференциальных уравнений $$begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}.$$

Ответ

$$begin{cases} x(t) = C_1 e^{3t} — C_2 e^t \ y(t) = C_1 e^{3t} + C_2e^{t} end{cases}, begin{cases} x(t) = 2e^{3t} — e^t \ y(t) = 2e^{3t} + e^t end{cases}$$

Метод Эйлера

Примерный алгоритм решения по данному методу следующий:

Построить матрицу $A$ из коэффициентов дифференциальных уравнений
Найти собственные значения $lambda$ и векторы матрицы $overline{x}$
Записать общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 $$

Рассмотрим данный метод решения на конкретном примере, так как практика учит лучше, чем теория.

Пример 4

Решить систему дифференциальных уравнений методом эйлера $$begin{cases} x’ = 2x+y \ y’ = 3x+4y end{cases}.$$

Решение

Первым делом нужно составить матрицу, элементы которой равны коэффициентам из правой части системы дифференциальных уравнений. $$A = begin{pmatrix} 2&1 \ 3&4 end{pmatrix}$$

Далее нужно найти собственные значения матрицы. Для этого необходимо составить характеристический многочлен и вычислить его корни. $$|A-lambda E| = 0 Rightarrow begin{vmatrix} 2 — lambda & 1 \ 3 & 4-lambda end{vmatrix} = 0$$

Раскрываем определитель два на два и решаем квадратное уравнение. $$(2-lambda)(4-lambda)-3 = 0,$$ $$8-2lambda -4lambda+lambda^2 — 3 = 0,$$ $$lambda^2 — 6lambda + 5 = 0,$$ $$lambda_{1,2} = frac{6pm sqrt{36-4 cdot 5}}{2} = frac{6pm 4}{2},$$ $$lambda_1 = 1, lambda_2 = 5.$$ Зная собственные значения матрицы получим собственные векторы матрицы по формуле $(A-lambda E)overline{x} = 0$.

1) Для $lambda_1 = 1$ имеем $$(A-lambda_1 E)overline{x}_1 = 0 Rightarrow begin{cases} x_1 + x_2 = 0 \ 3x_1 + 3x_2 = 0 end{cases}$$ Видим, что после сокращения второго уравнения на 3 получится, что первое уравнение равно второму. $$x_1 + x_2 = 0 Rightarrow x_1 = -x_2$$ Так как $x_2$ свободный, то положим его $x_2 = 1$. Тогда $x_1 = -1$. Отсюда следует, что первый собственный вектор равен $$overline{x}_1 = begin{pmatrix} -1 \ 1 end{pmatrix}.$$

2) Для $lambda_2 = 5$ имеем $$(A-lambda_2 E)overline{x}_2 = 0 Rightarrow begin{cases} -3x_1 + x_2 = 0 \ 3x_1 — x_2 = 0 end{cases}$$ Замечаем, что первое уравнение одно и тоже что второе, если домножить на (-1) одно из них. $$3x_1 — x_2 = 0 Rightarrow x_1 = frac{x_2}{3}$$ Так как $x_2$ свободный, то зададим его $x_2 = 3$. Таким образом $x_1 = 1$. Из этих значений получаем второй собственный вектор $$overline{x}_2 = begin{pmatrix} 1 \ 3 end{pmatrix}.$$

Находим общее решение системы дифференциальных уравнений по формуле $$begin{pmatrix} x(t) \ y(t) end{pmatrix} = C_1 e^{lambda_1 t} overline{x}_1 + C_2 e^{lambda_2 t} overline{x}_2 = $$ $$ = C_1 e^t begin{pmatrix} -1 \ 1 end{pmatrix} + C_2 e^{5t} begin{pmatrix} 1\3 end{pmatrix} = begin{pmatrix} -C_1 e^t \ C_1e^t end{pmatrix} + begin{pmatrix} C_2 e^{5t} \ 3C_2 e^{5t} end{pmatrix} = $$ $$ = begin{pmatrix} -C_1 e^t + C_2 e^{5t} \ C_1 e^t + 3C_2 e^{5t} end{pmatrix} Rightarrow begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$

Ответ

$$begin{cases} x(t) = -C_1 e^t + C_2 e^{5t} \ y(t) = C_1 e^t + 3C_2 e^{5t} end{cases}$$

Источник