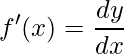diff
Differentiate symbolic expression or function
Syntax
Description
example
Df = diff(f)
differentiates f with respect to the symbolic scalar
variable determined by symvar(f,1).
example
Df = diff(f,n)
computes the nth derivative of f with
respect to the symbolic scalar variable determined by
symvar.
example
Df = diff(f,var)
differentiates f with respect to the differentiation
parameter var. var can be a symbolic
scalar variable, such as x, a symbolic function, such as
f(x), or a derivative function, such as
diff(f(t),t).
example
Df = diff(f,var,n)
computes the nth derivative of f with
respect to var.
example
Df = diff(f,var1,...,varN)
differentiates f with respect to the parameters
var1,...,varN.
example
Df = diff(f,mvar)
differentiates f with respect to the symbolic matrix
variable mvar of type symmatrix
Examples
collapse all
Differentiate Function
Find the derivative of the function sin(x^2).
syms f(x)
f(x) = sin(x^2);
Df = diff(f,x)
Find the value of the derivative at x = 2. Convert the value to double.
Differentiate with Respect to Particular Variable
Find the first derivative of this expression.
syms x t Df = diff(sin(x*t^2))
Because you did not specify the differentiation variable, diff uses the default variable defined by symvar. For this expression, the default variable is x.
var = symvar(sin(x*t^2),1)
Now, find the derivative of this expression with respect to the variable t.
Higher-Order Derivatives of Univariate Expression
Find the 4th, 5th, and 6th derivatives of t6.
Higher-Order Derivatives of Multivariate Expression with Respect to Particular Variable
Find the second derivative of this expression with respect to the variable y.
syms x y Df = diff(x*cos(x*y), y, 2)
Higher-Order Derivatives of Multivariate Expression with Respect to Default Variable
Compute the second derivative of the expression x*y. If you do not specify the differentiation variable, diff uses the variable determined by symvar. For this expression, symvar(x*y,1) returns x. Therefore, diff computes the second derivative of x*y with respect to x.
syms x y Df = diff(x*y,2)
If you use nested diff calls and do not specify the differentiation variable, diff determines the differentiation variable for each call. For example, differentiate the expression x*y by calling the diff function twice.
In the first call, diff differentiates x*y with respect to x, and returns y. In the second call, diff differentiates y with respect to y, and returns 1.
Thus, diff(x*y,2) is equivalent to diff(x*y,x,x), and diff(diff(x*y)) is equivalent to diff(x*y,x,y).
Mixed Derivatives
Differentiate this expression with respect to the variables x and y.
syms x y Df = diff(x*sin(x*y),x,y)
Df = 2 x cos(x y)-x2 y sin(x y)
You also can compute mixed higher-order derivatives by providing all differentiation variables.
syms x y Df = diff(x*sin(x*y),x,x,x,y)
Df = x2 y3 sin(x y)-6 x y2 cos(x y)-6 y sin(x y)
Differentiate with Respect to Function and Derivative
Find the derivative of the function y=f(x)2dfdx with respect to f(x).
syms f(x) y y = f(x)^2*diff(f(x),x); Dy = diff(y,f(x))
Find the 2nd derivative of the function y=f(x)2dfdx with respect to f(x).
Find the mixed derivative of the function y=f(x)2dfdx with respect to f(x) and dfdx.
Dy3 = diff(y,f(x),diff(f(x)))
Euler–Lagrange Equation
Find the Euler–Lagrange equation that describes the motion of a mass-spring system. Define the kinetic and potential energy of the system.
syms x(t) m k T = m/2*diff(x(t),t)^2; V = k/2*x(t)^2;
Define the Lagrangian.
L =m ∂∂t x(t)22-k x(t)22
The Euler–Lagrange equation is given by
0=ddt∂L(t,x,x˙)∂x˙-∂L(t,x,x˙)∂x
Evaluate the term ∂L/∂x˙.
D1 = diff(L,diff(x(t),t))
Evaluate the second term ∂L/∂x.
Find the Euler–Lagrange equation of motion of the mass-spring system.
ans(t) =m ∂2∂t2 x(t)+k x(t)=0
Differentiate with Respect to Vectors
To evaluate derivatives with respect to vectors, you can use symbolic matrix variables. For example, find the derivatives ∂α/∂x and ∂α/∂y for the expression α=yTAx, where y is a 3-by-1 vector, A is a 3-by-4 matrix, and x is a 4-by-1 vector.
Create three symbolic matrix variables x, y, and A, of the appropriate sizes, and use them to define alpha.
syms x [4 1] matrix syms y [3 1] matrix syms A [3 4] matrix alpha = y.'*A*x
Find the derivative of alpha with respect to the vectors x and y.
Differentiate with Respect to Matrix
To evaluate a derivative with respect to a matrix, you can use symbolic matrix variables. For example, find the derivative ∂Y/∂A for the expression Y=XTAX, where X is a 3-by-1 vector, and A is a 3-by-3 matrix. Here, Y is a scalar that is a function of the vector X and the matrix A.
Create two symbolic matrix variables to represent X and A. Define Y.
syms X [3 1] matrix syms A [3 3] matrix Y = X.'*A*X
Find the derivative of Y with respect to the matrix A.
The result is a Kronecker tensor product between XT and X, which is a 3-by-3 matrix.
Differentiate Symbolic Matrix Function
Differentiate a symbolic matrix function with respect to its matrix argument.
Find the derivative of the function t(X)=A⋅sin(B⋅X), where A is a 1-by-3 matrix, B is a 3-by-2 matrix, and X is a 2-by-1 matrix. Create A, B, and X as symbolic matrix variables and t(X) as a symbolic matrix function.
syms A [1 3] matrix syms B [3 2] matrix syms X [2 1] matrix syms t(X) [1 1] matrix keepargs t(X) = A*sin(B*X)
Differentiate the function with respect to X using diff.
Input Arguments
collapse all
f — Expression or function to differentiate
symbolic expression | symbolic function | symbolic vector | symbolic matrix | symbolic matrix variable | symbolic matrix function
Expression or function to differentiate, specified as one of these values:
-
a symbolic expression
-
a symbolic function
-
a symbolic vector or a symbolic matrix (a vector or a matrix
of symbolic expressions or functions) -
a symbolic matrix variable
-
a symbolic matrix function
If f is a symbolic vector or matrix,
diff differentiates each element of
f and returns a vector or a matrix of the same size
as f.
Data Types: single | double | sym | symfun | symmatrix | symfunmatrix
n — Order of derivative
nonnegative integer
Order of derivative, specified as a nonnegative integer.
var — Differentiation parameter
symbolic scalar variable | symbolic function | derivative function
Differentiation parameter, specified as a symbolic scalar variable,
symbolic function, or a derivative function created using the
diff function.
If you specify differentiation with respect to the symbolic function
var = f(x) or the derivative function var =, then the first argument
diff(f(x),x)f
must not contain any of these:
-
Integral transforms, such as
fourier,
ifourier,laplace,
ilaplace,htrans,
ihtrans,ztrans, and
iztrans -
Unevaluated symbolic expressions that include
limitorint -
Symbolic functions evaluated at a specific point, such as
f(3)org(0)
Data Types: single | double | sym | symfun
var1,...,varN — Differentiation parameters
symbolic scalar variables | symbolic functions | derivative functions
Differentiation parameters, specified as symbolic scalar variables,
symbolic functions, or derivative functions created using the
diff function.
Data Types: single | double | sym | symfun
mvar — Differentiation parameter
symbolic matrix variable
Differentiation parameter, specified as a symbolic matrix variable.
When using a symbolic matrix variable as the differentiation parameter,
f must be a differentiable scalar function, where
mvar can represent a scalar, vector, or matrix. The
derivative of f cannot be a tensor or a matrix in terms
of tensors. For example, see Differentiate with Respect to Vectors and
Differentiate with Respect to Matrix.
Data Types: symmatrix
Limitations
-
The
difffunction does not support tensor derivatives when
using a symbolic matrix variable as the differentiation parameter. If the
derivative is a tensor, or the derivative is a matrix in terms of tensors, then
thedifffunction will error.
Tips
-
When computing mixed higher-order derivatives with more than one variable, do
not usento specify the order of derivative. Instead,
specify all differentiation variables explicitly. -
To improve performance,
diffassumes
that all mixed derivatives commute. For example,This assumption suffices for most engineering and
scientific problems. -
If you differentiate a multivariate expression or function
fwithout specifying the differentiation variable, then a
nested call todiffanddiff(f,n)can
return different results. The reason is that in a nested call, each
differentiation step determines and uses its own differentiation variable. In
calls likediff(f,n), the differentiation variable is
determined once bysymvar(f,1)and used for all
differentiation steps. -
If you differentiate an expression or function containing
absorsign, the arguments must be
real values. For complex arguments ofabsand
sign, thedifffunction formally
computes the derivative, but this result is not generally valid because
absandsignare not
differentiable over complex numbers.
Version History
Introduced before R2006a
Дифференцирование
Чтобы проиллюстрировать, как взять производные с помощью программного обеспечения Symbolic Math Toolbox™, сначала создайте символьное выражение:
Команда
дифференцирует f относительно x:
Как другой пример, позволить
где exp(x) обозначает ex, и дифференцируйте g:
y = exp(x)*cos(x) - exp(x)*sin(x)
Найти производную g для данного значения x, замените x для использования значения subs и возвратите использование численного значения vpa. Найдите производную g в x = 2.
ans = -9.7937820180676088383807818261614
Взять вторую производную g, войти
Можно получить тот же результат путем взятия производной дважды:
В этом примере, MATLAB® программное обеспечение автоматически упрощает ответ. Однако в некоторых случаях MATLAB не может упростить ответ, в этом случае можно использовать simplify команда. Для примера такого упрощения смотрите Больше Примеров.
Обратите внимание на то, что, чтобы взять производную константы, необходимо сначала задать константу как символьное выражение. Например, ввод
возвращается
Если вы только входите
MATLAB возвращается
потому что 5 не символьное выражение.
Производные выражений с несколькими переменными
Чтобы дифференцировать выражение, которое содержит больше чем одну символьную переменную, задайте переменную, относительно которой вы хотите дифференцироваться. diff команда затем вычисляет частную производную выражения относительно той переменной. Например, учитывая символьное выражение
команда
вычисляет частную производную ∂f/∂t. Результат
Дифференцировать f относительно переменной s, войти
который возвращается:
Если вы не задаете переменную, чтобы дифференцироваться относительно, MATLAB выбирает переменную по умолчанию. В основном переменная по умолчанию является буквой, самой близкой к x в алфавите. Смотрите полный набор правил в Находке Символьная Переменная По умолчанию. В предыдущем примере, diff(f) берет производную f относительно t потому что буква t ближе к x в алфавите, чем буква s . Чтобы определить переменную по умолчанию, относительно которой дифференцируется MATLAB, использовать symvar:
Вычислите вторую производную f относительно t:
Эта команда возвращается
Обратите внимание на то, что diff(f, 2) дает тот же ответ потому что t переменная по умолчанию.
Больше примеров
Далее проиллюстрировать diff команда, задайте aBXNT, и theta в рабочем пространстве MATLAB путем ввода
Эта таблица иллюстрирует результаты ввода diff(f).
|
f |
diff (f) |
|---|---|
syms x n f = x^n; |
diff(f) ans = n*x^(n - 1) |
syms a b t f = sin(a*t + b); |
diff(f) ans = a*cos(b + a*t) |
syms theta f = exp(i*theta); |
diff(f) ans = exp(theta*1i)*1i |
Дифференцировать функцию Бесселя первого рода, besselj(nu,z), относительно zВвод
syms nu z b = besselj(nu,z); db = diff(b)
который возвращается
db = (nu*besselj(nu, z))/z - besselj(nu + 1, z)
diff функция может также взять символьную матрицу в качестве своего входа. В этом случае дифференцирование сделано поэлементно. Рассмотрите пример
syms a x A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]
который возвращается
A = [ cos(a*x), sin(a*x)] [ -sin(a*x), cos(a*x)]
Команда
возвращается
ans = [ -a*sin(a*x), a*cos(a*x)] [ -a*cos(a*x), -a*sin(a*x)]
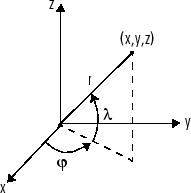
Можно также выполнить дифференцирование вектор-функции относительно аргумента вектора. Рассмотрите преобразование от Евклидова (x, y, z) к сферическому (r,λ,φ) координаты, как дано x=rcosλcosφ, y=rcosλsinϕ, и z=rsinλ. Обратите внимание на то, что λ соответствует вертикальному изменению или широте в то время как φ обозначает азимут или долготу.
Чтобы вычислить якобиевскую матрицу, J, этого преобразования, использует jacobian функция. Математическое обозначение for J
В целях синтаксиса тулбокса используйте l для λ и f для φ. Команды
syms r l f x = r*cos(l)*cos(f); y = r*cos(l)*sin(f); z = r*sin(l); J = jacobian([x; y; z], [r l f])
возвратите якобиан
J = [ cos(f)*cos(l), -r*cos(f)*sin(l), -r*cos(l)*sin(f)] [ cos(l)*sin(f), -r*sin(f)*sin(l), r*cos(f)*cos(l)] [ sin(l), r*cos(l), 0]
и команда
возвращается
Аргументы jacobian функция может быть вектор-столбцами или векторами-строками. Кроме того, поскольку определитель якобиана является довольно сложным тригонометрическим выражением, можно использовать simplify сделать тригонометрические замены и сокращения (упрощения).
Таблица, обобщающая diff и jacobian следует.
|
Математический оператор |
Команда MATLAB |
|---|---|
|
dfdx |
|
|
dfda |
|
|
d2fdb2 |
|
|
J=∂(r,t)∂(u,v) |
|
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Differentiation of a function y = f(x) tells us how the value of y changes with respect to change in x. It can also be termed as the slope of a function.
Derivative of a function f(x) wrt to x is represented as
MATLAB allows users to calculate the derivative of a function using diff() method. Different syntax of diff() method are:
- f’ = diff(f)
- f’ = diff(f, a)
- f’ = diff(f, b, 2)
f’ = diff(f)
It returns the derivative of function f(x) wrt variable x.
Example 1:
Matlab
syms x
f = cos(x);
disp("f(x) :");
disp(f);
d = diff(f);
disp("Derivative of f(x) :");
disp(d);
Output :
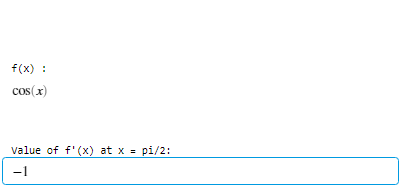
Example 2: Evaluating the derivative of a function at a specified value using subs(y,x,k).
- subs(y,x,k), it gives the value of function y at x = k.
Matlab
# variable x
syms x
f = cos(x);
disp("f(x) :");
disp(f);
d = diff(f);
val = subs(d,x,pi/2);
disp("Value of f'(x) at x = pi/2:");
disp(val);
Output :
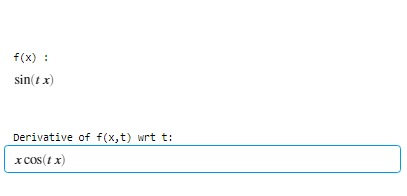
f’ = diff(f, a)
- It returns the derivative of function f with respect to variable a.
Matlab
syms x t;
f = sin(x*t);
disp("f(x) :");
disp(f);
d = diff(f,t);
disp("Derivative of f(x,t) wrt t:");
disp(d);
Output :
f’ = diff(f, b, 2)
It returns the double derivative of function f with respect to variable b.
Example 1:
Matlab
syms x n;
f = x^n;
disp("f(x,n) :");
disp(f);
d = diff(f,x,2);
disp("Double Derivative of f(x,n) wrt x:");
disp(d);
Output :
In the same way, you can also calculate the k-order derivative of function f using diff(f,x,k).
Example 2:
Calculating the partial derivative 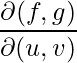
Matlab
syms u v;
f = u^2;
g = sin(v)*(3*u);
disp("f(u,v) :");
disp(f);
disp("g(u,v) :");
disp(g);
J = jacobian([f; g], [u v]);
disp("Jacobian matrix :");
disp(J);
d = det(J);
disp("Determinant of Jacobian matrix:");
disp(d);
Output :
Last Updated :
23 Aug, 2021
Like Article
Save Article
This example shows how to solve a transistor partial differential equation (PDE) and use the results to obtain partial derivatives that are part of solving a larger problem.
Consider the PDE
∂u∂t=D∂2u∂x2-DηL∂u∂x.
This equation arises in transistor theory [1], and u(x,t) is a function describing the concentration of excess charge carriers (or holes) in the base of a PNP transistor. D and η are physical constants. The equation holds on the interval 0≤x≤L for times t≥0.
The initial condition includes a constant K and is given by
u(x,0)=K LD(1-e-η(1-x/L)η).
The problem has boundary conditions given by
u(0,t)=u(L,t)=0.
For fixed x, the solution to the equation u(x,t) describes the collapse of excess charge as t→∞. This collapse produces a current, called the emitter discharge current, which has another constant Ip:
I(t)=[IpDK∂∂xu(x,t)]x=0.
The equation is valid for t>0 due to the inconsistency in the boundary values at x=0 for t=0 and t>0. Since the PDE has a closed-form series solution for u(x,t), you can calculate the emitter discharge current analytically as well as numerically, and compare the results.
To solve this problem in MATLAB®, you need to code the PDE equation, initial conditions, and boundary conditions, then select a suitable solution mesh before calling the solver pdepe. You either can include the required functions as local functions at the end of a file (as done here), or save them as separate, named files in a directory on the MATLAB path.
Define Physical Constants
To keep track of the physical constants, create a structure array with fields for each one. When you later define functions for the equations, the initial condition, and the boundary conditions, you can pass in this structure as an extra argument so that the functions have access to the constants.
C.L = 1; C.D = 0.1; C.eta = 10; C.K = 1; C.Ip = 1;
Code Equation
Before you can code the equation, you need to make sure that it is in the form that the pdepe solver expects:
c(x,t,u,∂u∂x)∂u∂t=x-m∂∂x(xmf(x,t,u,∂u∂x))+s(x,t,u,∂u∂x).
In this form, the PDE is
∂u∂t=x0 ∂∂x(x0 D∂u∂x)-DηL∂u∂x.
So the values of the coefficients in the equation are
-
m=0 (Cartesian coordinates with no angular symmetry)
-
c(x,t,u,∂u∂x)=1
-
f(x,t,u,∂u∂x)=D∂u∂x
-
s(x,t,u,∂u∂x)=-DηL∂u∂x
Now you can create a function to code the equation. The function should have the signature [c,f,s] = transistorPDE(x,t,u,dudx,C):
-
xis the independent spatial variable. -
tis the independent time variable. -
uis the dependent variable being differentiated with respect toxandt. -
dudxis the partial spatial derivative ∂u/∂x. -
Cis an extra input containing the physical constants. -
The outputs
c,f, andscorrespond to coefficients in the standard PDE equation form expected bypdepe.
As a result, the equation in this example can be represented by the function:
function [c,f,s] = transistorPDE(x,t,u,dudx,C) D = C.D; eta = C.eta; L = C.L; c = 1; f = D*dudx; s = -(D*eta/L)*dudx; end
(Note: All functions are included as local functions at the end of the example.)
Code Initial Condition
Next, write a function that returns the initial condition. The initial condition is applied at the first time value, and provides the value of u(x,t0) for any value of x. Use the function signature u0 = transistorIC(x,C) to write the function.
The initial condition is
u(x,0)=K LD(1-e-η(1-x/L)η).
The corresponding function is
function u0 = transistorIC(x,C) K = C.K; L = C.L; D = C.D; eta = C.eta; u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta; end
Code Boundary Conditions
Now, write a function that evaluates the boundary conditions u(0,t)=u(1,t)=0. For problems posed on the interval a≤x≤b, the boundary conditions apply for all t and either x=a or x=b. The standard form for the boundary conditions expected by the solver is
p(x,t,u)+q(x,t)f(x,t,u,∂u∂x)=0.
Written in this form, the boundary conditions for this problem are
— For x=0, the equation is u+0⋅d∂u∂x=0. The coefficients are:
-
pL(x,t,u)=u,
-
qL(x,t)=0.
— Likewise for x=1, the equation is u+0⋅d∂u∂x=0. The coefficients are:
-
pR(x,t,u)=u,
-
qR(x,t)=0.
The boundary function should use the function signature [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t):
-
The inputs x
land ulcorrespond to x and u for the left boundary. -
The inputs
xrandurcorrespond to x and u for the right boundary. -
tis the independent time variable. -
The outputs
plandqlcorrespond to pL(x,t,u) and qL(x,t) for the left boundary (x=0 for this problem). -
The outputs
prandqrcorrespond to pR(x,t,u) and qR(x,t) for the right boundary (x=1 for this problem).
The boundary conditions in this example are represented by the function:
function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) pl = ul; ql = 0; pr = ur; qr = 0; end
Select Solution Mesh
The solution mesh defines the values of x and t where the solution is evaluated by the solver. Since the solution to this problem changes rapidly, use a relatively fine mesh of 50 spatial points in the interval 0≤x≤L and 50 time points in the interval 0≤t≤1.
x = linspace(0,C.L,50); t = linspace(0,1,50);
Solve Equation
Finally, solve the equation using the symmetry m, the PDE equation, the initial condition, the boundary conditions, and the meshes for x and t. Since pdepe expects the PDE function to use four inputs and the initial condition function to use one input, create function handles that pass in the structure of physical constants as an extra input.
m = 0; eqn = @(x,t,u,dudx) transistorPDE(x,t,u,dudx,C); ic = @(x) transistorIC(x,C); sol = pdepe(m,eqn,ic,@transistorBC,x,t);
pdepe returns the solution in a 3-D array sol, where sol(i,j,k) approximates the kth component of the solution uk evaluated at t(i) and x(j). For this problem u has only one component, but in general you can extract the kth solution component with the command u = sol(:,:,k).
Plot Solution
Create a surface plot of the solution u plotted at the selected mesh points for x and t.
surf(x,t,u) title('Numerical Solution (50 mesh points)') xlabel('Distance x') ylabel('Time t') zlabel('Solution u(x,t)')
Now, plot just x and u to get a side view of the contours in the surface plot.
plot(x,u) xlabel('Distance x') ylabel('Solution u(x,t)') title('Solution profiles at several times')
Compute Emitter Discharge Current
Using a series solution for u(x,t), the emitter discharge current can be expressed as the infinite series [1]:
I(t)=2π2Ip(1-e-ηη)∑n=1∞n2n2π2+η2/4e-dtL2(n2π2+η2/4).
Write a function to calculate the analytic solution for I(t) using 40 terms in the series. The only variable is time, but specify a second input to the function for the structure of constants.
function It = serex3(t,C) % Approximate I(t) by series expansion. Ip = C.Ip; eta = C.eta; D = C.D; L = C.L; It = 0; for n = 1:40 % Use 40 terms m = (n*pi)^2 + 0.25*eta^2; It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t); end It = 2*Ip*((1 - exp(-eta))/eta)*It; end
Using the numeric solution for u(x,t) as computed by pdepe, you can also calculate the numeric approximation for I(t) at x=0 with
I(t)=[IpDK∂∂xu(x,t)]x=0.
Calculate the analytic and numeric solutions for I(t) and plot the results. Use pdeval to compute the value of ∂u/∂x at x=0.
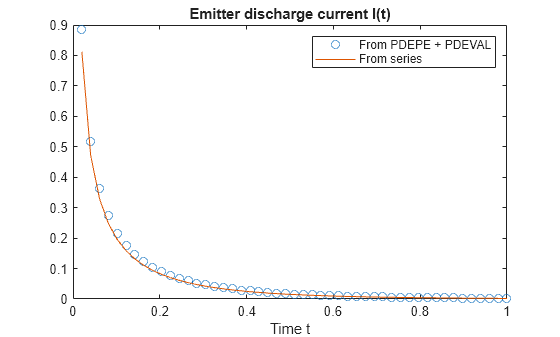
nt = length(t); I = zeros(1,nt); seriesI = zeros(1,nt); iok = 2:nt; for j = iok % At time t(j), compute du/dx at x = 0. [~,I(j)] = pdeval(m,x,u(j,:),0); seriesI(j) = serex3(t(j),C); end % Numeric solution has form I(t) = (I_p*D/K)*du(0,t)/dx I = (C.Ip*C.D/C.K)*I; plot(t(iok),I(iok),'o',t(iok),seriesI(iok)) legend('From PDEPE + PDEVAL','From series') title('Emitter discharge current I(t)') xlabel('Time t')
The results match reasonably well. You can further improve the numeric result from pdepe by using a finer solution mesh.
Local Functions
Listed here are the local helper functions that the PDE solver pdepe calls to calculate the solution. Alternatively, you can save these functions as their own files in a directory on the MATLAB path.
function [c,f,s] = transistorPDE(x,t,u,dudx,C) % Equation to solve D = C.D; eta = C.eta; L = C.L; c = 1; f = D*dudx; s = -(D*eta/L)*dudx; end % ---------------------------------------------------- function u0 = transistorIC(x,C) % Initial condition K = C.K; L = C.L; D = C.D; eta = C.eta; u0 = (K*L/D)*(1 - exp(-eta*(1 - x/L)))/eta; end % ---------------------------------------------------- function [pl,ql,pr,qr] = transistorBC(xl,ul,xr,ur,t) % Boundary conditions pl = ul; ql = 0; pr = ur; qr = 0; end % ---------------------------------------------------- function It = serex3(t,C) % Approximate I(t) by series expansion. Ip = C.Ip; eta = C.eta; D = C.D; L = C.L; It = 0; for n = 1:40 % Use 40 terms m = (n*pi)^2 + 0.25*eta^2; It = It + ((n*pi)^2 / m)* exp(-(D/L^2)*m*t); end It = 2*Ip*((1 - exp(-eta))/eta)*It; end % ----------------------------------------------------
References
[1] Zachmanoglou, E.C. and D.L. Thoe. Introduction to Partial Differential Equations with Applications. Dover, New York, 1986.
See Also
pdepe
Related Topics
- Solving Partial Differential Equations
- Solve System of PDEs
Как в Matlab вычислить в символьном виде предел, производную, интеграл, разложить функцию в степенном виде? (В1Б5,В2Б12,В3Б24).
Вычисление пределов – команда limit
Для вычисления пределов функции F(x), заданной в аналитическом (символьном) виде, служит команда limit, которая используется в одном из следующих вариантов:
limit(F,x,a) – возвращает предел символьного выражения F в точке x =a;
limit(F,x,a,’right’) или limit(F,x,a,’left’) – возвращает предел в точке a справа или слева.
Продемонстрируем приемы вычисления пределов на следующих примерах:
Решения в указанном порядке имеют вид:
Здесь переменная NaN означает, что предела функции в точке x = 1 не существует.
Правосторонний предел функции в точке x = 1 существует и равен — ∞.
Левосторонний предел функции в точке x=1 существует и равен +∞.
Вычисление производных – команда diff
Для вычисления в символьном виде производных от выражения S служит команда diff, записываемая в форме diff(S, x, n). Она возвращает символьное значение n-ой производной (производной степени n) от символьного выражения или массива символьных выражений S по переменной x, т. е.
В формате diff(S, x) находится первая производная (n = 1 по умолчанию).
Найти первую и третью производные функции y = x 2 sinx.
Если S массив, то diff возвращает массив, элементами которого являются производные от исходных функций, образующих массив.
Если выражение S зависит от нескольких переменных, например, S=S(x,y), то ее частная производная (или S’x(x,y) ) по аргументу x есть производная этой функции по x при постоянном значении y.
В декартовой системе координат на плоскости xOy градиент функции S(x,y) есть вектор
Частными производными второго порядка функции S=S(x,y) называются частные производные от ее первых производных , , т. е.
Частные производные второго порядка обозначаются также символами
S»xx(x,y), S»xy(x,y), S»yx(x,y), S»yy(x,y). Аналогично определяются и обозначаются частные производные более высоких порядков. Смешанные производные второго порядка, отличающиеся только порядком дифференцирования, равны между собой при условии их непрерывности: S»xy(x,y) = S»yx(x,y).
Рассмотрим пример. Для функции двух переменных
найти gradf(x;y) и вычислить его в точке (0;0). Проверить выполнение условия f»xy(x,y) = f»yx(x,y).
Т. е. = . Тогда grad(arcsinxy) = .
Вычисление интегралов – команда int
В ряде случаев возникает необходимость вычисления неопределенных и определенных интегралов
Здесь f(x) – подынтегральная функция независимой переменной x, a нижний и b верхний пределы интегрирования для определенного интеграла.
Командаint(f, x)возвращает неопределенный интеграл (первообразную функцию) от символьного выражения f по переменной x.
Командаint(f, x, a, b) возвращает значение определенного интеграла от символьного выражения f по переменной x с пределами от а до b.
Подынтегральная функция f может зависеть от символьных параметров, а также быть массивом символьных выражений.
Если f массив, то int(f, x) возвращает массив первообразных, а int(f, x, a, b) – массив значений определенных интегралов. Примеры:
Вычисление производной и экстремумов функции в Matlab
Вычисление производной функции
В библиотеке Matlab есть специальная функция diff , которая выполняет аппроксимацию производных конечными разностями. Она имеет несколько синтаксических конструкций:
— diff(X) — возвращает конечные разности смежных элементов массива X. Если X — вектор, то diff(X) возвращает вектор разностей соседних элементов [Х(2)-Х(1) Х(3)-Х(2) . X(n)-X(n-D], у которого количество элементов на единицу меньше, чем у исходного вектора X.
Если X — матрица, то diff(X) возвращает матрицу разностей столбцов: [X(2:m, :)-X(l:m-l. :)];
— diff(X,n,dim) — возвращает конечные разности для матрицы X по строкам или по столбцам в зависимости от значения параметра dim. Если порядок n равен величине dim или превышает ее, то diff возвращает пустой массив.
Пример. Применяя функцию diff, вычислим производную функции
Введем идентификаторы переменных:
— x – переменная для хранения значения величины аргумента x, для которого вычисляется производная функции,
— dx – переменная для хранения конечного приращения,
— Y — переменная для хранения вычисленных значений функции,
— D — переменная для хранения вычисленного значения производной.
Код инструкции и полученный результат приведены ниже (рис. 1).
Вычисление локальных экстремумов
Напомним, что функция Y=f(x ) имеет экстремум в точке Х , если производная функции в этой точке равна нулю.
Задача вычисления локальных экстремумов исследуемой (целевой) функции в Matlab сводится к вычислению значения ее аргумента, при котором функция принимает минимальное (максимальное) значение с последующей проверкой существования экстремума путем вычисления производной в найденной точке.
Для решения первой задачи в системе Matlab используется функция [X.fval.exitflag,output] = fminbnd(@fun.x1,x2.options, p1,p2. ) , имеющая следующие синтаксические конструкции:
— fminbnd(@fun,xl,x2) — возвращает значение х , которое является локальным минимумом функции fun(x) на интервале xl > options=optimset(‘tolX’,1.е-10);
[x]=fminbnd(@cos.3,4,options)
х = 3.1416
Для вычисления экстремума функции y= x^2+x +2 выполним следующие операции:
— так как исследуемая функция в параметре функции fminbnd Matlab указывается в форме дескриптора, то создадим m-файл с кодом функции:
% функция y= x^2+x +2
function urav=fun1(x)
urav=x.^2+x +2;
— сохраним файл, присвоив ему имя fun1.m (рис. 2);
— чтобы выяснить, являются экстремумы исследуемой функции максимумами или минимумами, построим в заданном интервале x ее график (рис. 3), введя в командном окне инструкцию
>> fplot(@fun1, [-1 1]); grid on
На графике видно, что примерно при x = -0,5 исследуемая функция имеет минимум;
— в командном окне Matlab введем код инструкции для вычисления минимума функции:
На рис. 4 показан результат в командном окне.
— вычислим производную исследуемой функции в точке x =-0,5, для этого в командном окне Matlab введем инструкцию:
Результат представлен в командном окне (рис. 5).
Полученное значение производной исследуемой функции в точке x = -0,5 равно нулю, следовательно, в этой точке функция имеет локальный экстремум.
Частные производные в matlab
Пример использования функции diff при вычислении максимума второй производной на отрезке [a, b]
3. Теоретическая оценка погрешности численного интегрирования
Рассмотрим примеры использования теоретической оценки погрешности интегрирования на примере двух задач.
Пример. Определить теоретическую погрешность численного интегрирования методом трапеций в случае одного элементарного отрезка интегрирования..
Теоретическая погрешность для метода трапеций составляет
В случае элементарного отрезка иртегрирования, если заданы пределы интегрирования и подинтегральная функция, задачу можно решить например следующим образом:
В результате получим
M2 =
16.4000
Погрешность
R =
0.1164
Т.о. теоретическая оценка абсолютной погрешности погрешности составляет 0.1 . В задаче 1 лабораторной работы вам предлагается убедиться, что данная теоретическая оценка действительно справедлива.
4. Численное интегрирование
Вычислительные формулы приведены в приложении . Их анализ показывает, что формулы для одного элементарного отрезка интегрирования не требуют каких либо новых знаний. Необходимо только приготовить m-функцию , в которой следует определить интегрируемую функцию. И конечно для оценки погрешности интегрирования следует знать точное значение интеграла (см. выше).
Случай формул для составного отрезка интегрирования более сложный. Здесь требуется вычислять значения сумм. Например в методе Симпсона
В языке программировани MATLAB, как и в других языках программирования, существует оператор цикла for , возможностей которого достаточно для решения поставленных задач.
Здесь для задания интегрируемой функции необходимо создать m — файл f.m
5. Численное интегрирование средствами MATLAB
В MATLAB реализованы множество современных методов численного интегрирования. Мы рассмотрим простейшие из них.
А. Метод трапеций. Метод трапеции реализован в MATLAB несколькими функциями:
Наиболее интересна последняя из них. Данная функция вычисляет интеграл от функции у(х) по х методом трапеций . Аргумент и функция задаются в виде векторов или х — в виде вектора, а у — в виде матрицы. Если у(х) — матрица, то функция возвращает вектор значений интеграла для каждого столбца матрицы.
Пример. Пусть подынтегральная функция имеет вид
у(х) = х*е x + ln(x) + 1
Необходимо вычислить определенный интеграл в диапазоне от 1 до 10 с шагом 0.5.
Решение:
Б. Метод Симпсона. Метод Симпсона реализован в MATLAB также несколькими функциями. Мы рассмотрим простейшую из них:
quad(‘fun’, a, b)
quad(‘fun’, a, b, tol)
- ‘fun’ — подынтегральная функция, взятая в одинарные кавычки;
- а, b — пределы интегрирования;
- tol — относительная погрешность, задаваемая пользователем; по умолчанию tol=10 -3 .
Пример. Вычислить интеграл от функции x+e x на отрезке [1, 2] с точностью 10 -5 .
quad(‘x+exp(x)’, 1, 2, 1e-5)
6. Правило Рунге оценки погрешности интегрирования
В формулах для оценки погрешности квадратурных формул R используются значения производных подинтегральной функции, что требует дополнительного анализа и вычислений. В связи с этим получило распространение практическое правило Рунге оценки погрешности.
- I – точное значение интеграла,
- I(n) – значение интеграла вычисленное при n узлах интегрирования h = (b-a)/n,
- I(2n) – значение интеграла вычисленное при 2*n узлах интегрирования, h = (b-a)/2n.
Необходимо определить, с какой точностью вычислен итеграл I(2n), т.е. найти абсолютную погрешность
Для непосредственно определения данной погрешности необходимо найти максимум модуля соответствующей производжной от интегрируемой функции на отрезке [a, b]. Часто это достаточно трудоемкий или вообще невозможный процесс. Напрмер если интегрируемая функция задана таблично. В таких случаях оценку погрешности величины I(2n) можно провести следующим образом:
Здесь m = 3 для методов средних прямоугольников и трапеций, m = 15 для метода Симпсона.
Примечание. Если решается задача численного вычисления интеграла с заданной точностью, процесс удвоения числа узлов интегрирования продолжается до тех пор, пока величена не станет меньше заданной погрешности.
Как получить производную от функции в MATLAB?
В реальной жизни это кусок пирога, но как вы получаете производную от квадратичной или кубической функции в matlab?
Например, A*x^3 + B*x^2 + C*x + D будет 3*Ax^2 + 2*b*x + C
Я хочу получить это в matlab, но я не могу понять, как: (
например, я пробовал этот код, но я получаю глупый результат (возможно, я тот, кого следует обвинять!):
Обычно это должно давать [18 6 2]?? Также я хочу знать, как это сделать для диапазона чисел. Например, я хочу, чтобы производная каждой точки для примера выше для n = linspace(0,10,1000)
Обновление конечно, я могу сделать это вручную, но мне очень нравится знать, как это сделать с самой Matlab.
То, что я делаю сейчас, это получить касательную строку вышеприведенного примера, и я делаю это, и это работает:
Я имею в виду, что я должен использовать вместо ручной вычисляемой производной в этой строке:
4 ответа
3 Решение Max [2012-03-20 11:56:00]
Чтобы получить производную от полинома, который сам по себе является полиномом, используйте функцию Matlab polyder() . Это принимает стандартное представление полиномиальных коэффициентов как вектор и возвращает его производную в качестве второго вектора коэффи циента. Вы можете оценить производную от полинома p при некотором значении x следующим образом:
3 ely [2012-03-20 04:26:00]
Вы хотите проверить символическую библиотеку Matlab (на основе механизма Maple). Основная идея заключается в том, что вы захотите создать символические переменные ( «syms» ), а затем символически различать эти выражения. Затем вы можете конвертировать между вашим символическим выражением и дескриптором функции, который будет оценивать ваше символическое выражение при некоторых значениях координат. См. здесь для инструкций по синтаксису, библиотеке syms и т.д.
В реальных приложениях, как правило, вам необходимо написать свою собственную программную функцию для различных математических функций, с которыми вы имеете дело. Тогда только в особых случаях вы сможете аналитически вычислить производные, и в этих случаях вы захотите написать другую, отдельную программную функцию для математической функции, которая является производной. Символические библиотеки обычно очень медленные, и они (по крайней мере в настоящее время) являются неэффективным способом генерации фактических функций с помощью дескрипторов.
Если все, с чем вы когда-либо работаете, являются многочленами, это достаточно особый случай, когда вы должны иметь возможность написать общую функцию Matlab, которая принимает список коэффициентов и диапазон значений в качестве входных данных, и выводит производный коэффициент, плюс производная функция, оцененная по этим значениям. Вот пример:
Вы можете сделать это численно, используя конечные различия. MATLAB имеет функцию gradient , которая включает в себя точную схему 2-го порядка — см. здесь.
Если бы вы искали более высокую точность, вы могли бы реализовать свою собственную схему более высокого порядка.
Надеюсь, что это поможет.
1 Dougal [2012-03-20 04:21:00]
diff дает разницу между последовательными элементами в списке: 3 — 6 — -3, 2 — 3 — -1 и т.д.
Вы можете использовать символическую панель инструментов, если она у вас есть. Или, если вам нужны только полиномы, это не так сложно написать сами:
Это просто умножает каждый коэффициент на его показатель ( fliplr меняет список), а затем сдвигает экспоненты вниз на один (перемещение элементов списка один вправо).
Это дает вам новое представление полинома. Чтобы оценить один из них в данной точке x , попробуйте