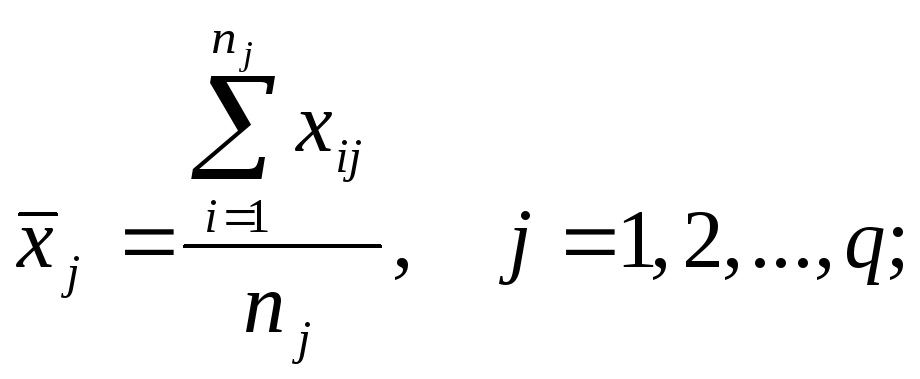Как найти частную среднюю - Исправление недочетов и поиск решений вместе с Examum.ru

Метод частных средних

Среднее, связанное
с определенными предположениями или
вычисленное при определенных условиях,
называется частным, условным или
групповым средним. Частные средние
переменных xиyвычисляются по формулам:

где
—
частное среднее переменнойxдля i–группы значений переменнойy(значения переменнойyразбитыqгрупп),—
частное среднее переменнойyдляp-группы
значений переменнойx(значения переменнойxразбиты наsгрупп);n_jиn_p– число отдельных значений в группеjи группеp;

Пример

Время наблюю-дения	№ наблюю-дения	y (общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб.	№ группы значений y	x (общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб.	№ группы значений x
январь	1	38,9	1	13,4	1
февраль	2	45,3	1	15,4	2
март	3	61,1	2	16,7	3
апрель	4	70,4	2	16,2	3
май	5	63,8	2	13,0	1
июнь	6	67,7	2	15,0	2
июль	7	70,6	2	20,8	5
август	8	78,9	3	16,4	3
сентябрь	9	73,2	3	17,4	4
октябрь	10	78,1	3	23,6	6
ноябрь	11	103,0	4	23,9	6
декабрь	12	133,4	5	34,4	7

Группировка
значений переменной yпостроена так, что вариация значений
переменнойy_iиy_jиз одной группы не превосходит 10.

Группировка
значений переменной xпостроена так, что вариация значений
переменнойx_iиx_jиз одной группы не превосходит 1.

Представим
полученные значения частных средних
графически. Для этого из точек,
соответствующих значениям переменной
x, нужно восставить
перпендикуляры к оси абсцисс и отложить
их на значения.
Вершины ординат нужно последовательно
соединить прямолинейными отрезками,
то есть прямое соединяем следующие
точки:

М₁(13,2; 42,1);
М₂(15,2; 42,1); М₃(16,4; 66,7); М₄(16,4;
66,7);

М₅(13,2; 66,7);
М₆(15,2; 66,7); М₇(20,8; 66,7); М₈(16,4;
76,7);

М₉(17,4; 76,7);
М₁₀(23,7; 76,7); М₁₁(23,7; 103,0); М₁₂(34,4;
133,4).

Эмпирическая линия
регрессии yнаx:

Эмпирическая линия
регрессии xнаyне совпадает с эмпирической линией
регрессииyнаx.
Поэтому при изучении зависимости
необходимо отмечать направление
зависимости между изучаемыми переменными.

Простая линейная регрессия

Простой регрессией
называется односторонняя стохастическая
зависимость результативной переменной
только от одной объясняющей переменной:

Простая линейная
регрессия задается следующей формулой:

b₀иb₁– неизвестные параметры регрессии;
имеютсяnнаблюдений
над переменнойx:x₁,x₂,
…,x_n;b₀выполняет в уравнении регрессии функцию
выравнивания;b₁характеризует наклон прямой к оси ОХ.

b₁– это мера, которая в среднем показывает
влияние изменения объясняющей переменнойxна зависимую
переменнуюy. При
экономических исследованиях чаще
интересуются не столько самой прямой
регрессии, сколько влиянием, которое
одно экономическое явление оказывает
на другое, т.е. речь идет о вычислении
коэффициентов регрессии.

Если b₁>0,
то регрессия является положительной,
приb₁<0
регрессия является отрицательной.
Значения функции регрессииŷ_i(предсказанные и рассчитанные) являются
оценками средних значений переменнойyдля некоторого
фиксированного значения переменнойx.

После экономического
анализа можно приступать к выравниванию
опытных данных, заключающемуся в
построении гипотетической линии. При
этом требуется минимизировать ошибки
при определении формы связи между
переменными. Эти ошибки обнаруживаются
через отклонения û_iэмпирических данных от значений регрессииŷ_i.
Они являются значениями возмущающей
переменнойu:

,
i
= 1, …, n.

В качестве меры
отклонения функции от набора наблюдений
можно взять:

сумму
квадратов отклонений:
сумму
модулей отклонений:
,
где g– некоторая мера.
Например, в качестве меры можно взять
функцию Хубера, которая при малых
отклонениях квадратична, а при больших
линейна:

Каждая из указанных
мер отклонений имеет свои недостатки
и достоинства. Мера суммы квадратов
отклонений обладает легкостью вычислений,
простотой математических выводов,
хорошими статистическими свойствами,
но чувствителен к выбросам.

Мера суммы модулей
не чувствительна к выбросам, но сложна
в вычислениях и неоднозначна.

Мера Хубера является
попыткой совместить достоинства двух
предыдущих методов.

Самым распространенным
и теоретически обоснованным является
метод нахождения коэффициентов, при
котором минимизируется первая сумма.
Он получил названия метода наименьших
квадратов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В статистике используют различные виды средних величин, которые делятся на два больших класса:

Степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадра-тическая, средняя кубическая);

Структурные средние (мода, медиана).

Для вычисления степенных средних
необходимо использовать все имеющиеся значения признака. Мода
и медиана
определяются лишь структурой распределения, поэтому их называют структурными, позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.

Самый распространенный вид средней величины – средняя арифметическая. Под средней арифметической
понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй – 7, третий – 4, четвертый – 10, пятый– 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для опреде-

ления средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна

Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную.
Например, рассчитаем средний возраст студентов в группе из 20 человек, возраст которых варьируется от 18 до 22 лет, где xi
– варианты осредняемого признака, fi
– частота, которая показывает, сколько раз встречается i-е
значение в совокупности (табл. 5.1).

Таблица 5.1

Средний возраст студентов

Применяя формулу средней арифметической взвешенной, получаем:

Для выбора средней арифметической взвешенной существует определенное правило: если имеется ряд данных по двум показателям, для одного из которых надо вычислить

среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя неизвестны, но могут быть найдены как произведение этих показателей, то средняя величина должна высчитывать-ся по формуле средней арифметической взвешенной.

В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины – средняя гармоническая.
В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники. Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.

Например, пусть известно, что автомобиль прошел первые 210 км со скоростью 70 км/ч, а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 360 км, используя формулу средней арифметической, нельзя. Так как вариантами являются скорости на отдельных участках xj
= 70 км/ч и Х2
= 75 км/ч, а весами (fi) считаются соответствующие отрезки пути, то произведения вариантов на веса не будут иметь ни физического, ни экономического смысла. В данном случае смысл приобретают частные от деления отрезков пути на соответствующие скорости (варианты xi), т. е. затраты времени на прохождение отдельных участков пути (fi/
xi). Если отрезки пути обозначить через fi, то весь путь выразиться как?fi, а время, затраченное на весь путь, – как? fi/
xi ,
Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени:

В нашем примере получим:

Если при использовании средней гармонической веса всех вариантов (f) равны, то вместо взвешенной можно использовать простую (невзвешенную) среднюю гармоническую:

где xi – отдельные варианты; n
– число вариантов осредняемого признака. В примере со скоростью простую среднюю гармоническую можно было бы применить, если бы были равны отрезки пути, пройденные с разной скоростью.

Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина некоторого итогового, обобщающего показателя, который связан с осредняемым показателем. Так, при замене фактических скоростей на отдельных отрезках пути их средней величиной (средней скоростью) не должно измениться общее расстояние.

Форма (формула) средней величины определяется характером (механизмом) взаимосвязи этого итогового показателя с осредняемым, поэтому итоговый показатель, величина которого не должна изменяться при замене вариантов их средней величиной, называется определяющим показателем.
Для вывода формулы средней нужно составить и решить уравнение, используя взаимосвязь осредняемого показателя с определяющим. Это уравнение строится путем замены вариантов осредняемого признака (показателя) их средней величиной.

Кроме средней арифметической и средней гармонической в статистике используются и другие виды (формы) средней величины. Все они являются частными случаями степенной средней.
Если рассчитывать все виды степенных средних величин для одних и тех же данных, то значения

их окажутся одинаковыми, здесь действует правило мажо-рантности
средних. С увеличением показателя степени средних увеличивается и сама средняя величина. Наиболее часто применяемые в практических исследованиях формулы вычисления различных видов степенных средних величин представлены в табл. 5.2.

Таблица 5.2

Виды степенных средних

Средняя геометрическая применяется, когда имеется n
коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста. Средняя геометрическая простая
рассчитывается по формуле

Формула средней геометрической взвешенной
имеет следующий вид:

Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.

Средняя квадратическая
применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле

Средняя квадратическая взвешенная
рассчитывается по другой формуле:

Средняя кубическая
применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

где – средняя величина; – индивидуальное значение; n
– число единиц изучаемой совокупности; k
– показатель степени, определяющий вид средней.

При использовании одних и тех же исходных данных, чем больше k
в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение:

Средние величины, описанные выше, дают обобщенное представление об изучаемой совокупности и с этой точки зрения их теоретическое, прикладное и познавательное значение бесспорно. Но бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому кроме рассмотренных средних в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном (ранжированном) ряду значений признака вполне определенное положение. Среди таких величин наиболее употребительными являются структурные,
или описательные, средние
– мода (Мо) и медиана (Ме).

Мода
– величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле

где х0 – нижняя граница интервала; h
– величина интервала; fm
– частота интервала; fm_
1 – частота предшествующего интервала; fm+
1 – частота следующего интервала.

Медианой
называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше ее. Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности. Задача нахождения медианы для дискретного вариационного ряда решается просто. Если всем единицам ряда придать порядковые номера, то порядковый номер медианного варианта определяется как (п +1) / 2 с нечетным числом членов п. Если же количество членов ряда является четным числом, то медианой будет являться среднее значение двух вариантов, имеющих порядковые номера n
/ 2 и n
/ 2 + 1.

При определении медианы в интервальных вариационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Расчет медианы интервального вариационного ряда производится по формуле

где X0
– нижняя граница интервала; h
– величина интервала; fm
– частота интервала; f
– число членов ряда;

M-1
– сумма накопленных членов ряда, предшествующих данному.

Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили
и децили.
Квартили делят ряд по сумме частот на 4 равные части, а децили – на 10 равных частей. Квартилей насчитывается три, а децилей – девять.

Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Эти, не очень характерные для совокупности значения вариантов, влияя на величину средней арифметической, не влияют на значения медианы и моды, что делает последние очень ценными для экономико-статистического анализа показателями.

В вычислении среднего значения теряется.

Среднее значение
набора чисел равно сумме чисел S, деленной на количество этих чисел. То есть получается, что среднее
значение
равно: 19/4 = 4.75.

Обратите внимание

Если потребуется найти среднее геометрическое всего для двух чисел, то инженерный калькулятор вам не понадобится: извлечь корень второй степени (квадратный корень) из любого числа можно при помощи самого обычного калькулятора.

Полезный совет

В отличие от среднего арифметического, на геометрическое среднее не так сильно влияют большие отклонения и колебания между отдельными значениями в исследуемом наборе показателей.

Источники:

Онлайн-калькулятор, рассчитывающий среднее геометрическое
среднее геометрическое формула

Среднее
значение — это одна из характеристик набора чисел. Представляет собой число, которое не может выходить за пределы диапазона, определяемого наибольшим и наименьшим значениями в этом наборе чисел. Среднее
арифметическое значение — наиболее часто используемая разновидность средних.

Инструкция

Сложите все числа множества и разделите их на количество слагаемых, чтобы получить среднее арифметическое значение. В зависимости от конкретных условий вычисления иногда проще делить каждое из чисел на количество значений множества и суммировать результат.

Используйте, например, входящий в состава ОС Windows , если вычислить среднее арифметическое значение в уме не представляется возможным. Открыть его можно с помощью диалога запуска программ. Для этого нажмите «горячие клавиши» WIN + R или щелкните кнопку «Пуск» и выберите в главном меню команду «Выполнить». Затем напечатайте в поле ввода calc и нажмите на Enter либо щелкните кнопку «OK». Это же можно сделать через главное меню — раскройте его, перейдите в раздел «Все программы» и в секции «Стандартные» и выберите строку «Калькулятор».

Введите последовательно все числа множества, нажимая после каждого из них (кроме последнего) клавишу «Плюс» или щелкая соответствующую кнопку в интерфейсе калькулятора. Вводить числа тоже можно как с клавиатуры, так и щелкая соответствующие кнопки интерфейса.

Нажмите клавишу с косой (слэш) или щелкните этот в интерфейсе калькулятора после ввода последнего значения множества и напечатайте количество чисел в последовательности. Затем нажмите знак равенства, и калькулятор рассчитает и покажет среднее арифметическое значение.

Можно для этой же цели использовать табличный редактор Microsoft Excel. В этом случае запустите редактор и введите в соседние ячейки все значения последовательности чисел. Если после ввода каждого числа вы будете нажимать Enter или клавишу со стрелкой вниз или вправо, то редактор сам будет перемещать фокус ввода в соседнюю ячейку.

Щелкните следующую за последним введенным числом ячейку, если вам не достаточно только увидеть среднее арифметическое значение. Раскройте выпадающий с изображением греческой сигма (Σ) команд «Редактирование» на вкладке «Главная». Выберите в нем строку «Среднее
» и редактор вставит нужную формулу для вычисления среднеарифметического значения в выделенную ячейку. Нажмите клавишу Enter, и значение будет рассчитано.

Среднее арифметическое — одна из мер центральной тенденции, широко используемая в математике и статистических расчетах. Найти среднее арифметическое число для нескольких значений очень просто, но у каждой задачи есть свои нюансы, знать которые для выполнения верных расчетов просто необходимо.

Что такое среднее арифметическое число

Среднее арифметическое число определяет усредненное значение для всего исходного массива чисел. Другими словами, из некоторого множества чисел выбирается общее для всех элементов значение, математическое сравнение которого со всеми элементами носит приближенно равный характер. Среднее арифметическое число используется, преимущественно, при составлении финансовых и статистических отчетов или для расчетов результатов проведенных подобных опытов.

Как найти среднее арифметическое число

Поиск среднего арифметического числа для массива чисел следует начинать с определения алгебраической суммы этих значений. К примеру, если в массиве присутствуют числа 23, 43, 10, 74 и 34, то их алгебраическая сумма будет равна 184. При записи среднее арифметическое обозначается буквой μ (мю) или x
(икс с чертой). Далее алгебраическую сумму следует разделить на количество чисел в массиве. В рассматриваемом примере чисел было пять, поэтому среднее арифметическое будет равно 184/5 и составит 36,8.

Особенности работы с отрицательными числами

Если в массиве присутствуют отрицательные числа, то нахождение среднего арифметического значения происходит по аналогичному алгоритму. Разница имеется только при рассчетах в среде программирования, или же если в задаче есть дополнительные условия. В этих случаях нахождение среднего арифметического чисел с разными знаками сводится к трем действиям:

1. Нахождение общего среднего арифметического числа стандартным методом;
2. Нахождение среднего арифметического отрицательным чисел.
3. Вычисление среднего арифметического положительных чисел.

Ответы каждого из действий записываются через запятую.

Натуральные и десятичные дроби

Если массив чисел представлен десятичными дробями, решение происходит по методу вычисления среднего арифметического целых чисел, но сокращение результата производится по требованиям задачи к точности ответа.

При работе с натуральными дробями их следует привести к общему знаменателю, который умножается на количество чисел в массиве. В числителе ответа будет сумма приведенных числителей исходных дробных элементов.

Инженерный калькулятор.

Инструкция

Учитывайте, что в общем случае среднее геометрическое чисел находится путем перемножения этих чисел и извлечения из них корня степени, которая соответствует количеству чисел. Например, если нужно найти среднее геометрическое пяти чисел, то из произведения нужно будет извлекать корень степени.

Для нахождения среднего геометрического двух чисел используйте основное правило. Найдите их произведение, после чего извлеките из него квадратный корень, поскольку числа два, что соответствует степени корня. Например, для того чтобы найти среднее геометрическое чисел 16 и 4, найдите их произведение 16 4=64. Из получившегося числа извлеките квадратный корень √64=8. Это и будет искомая величина. Обратите внимание на то, что среднее арифметическое этих двух чисел больше и равно 10. Если корень не извлекается нацело, произведите округление результата до нужного порядка.

Чтобы найти среднее геометрическое более чем двух чисел, тоже используйте основное правило. Для этого найдите произведение всех чисел, для которых нужно найти среднее геометрическое. Из полученного произведения извлеките корень степени, равной количеству чисел. Например, чтобы найти среднее геометрическое чисел 2, 4 и 64, найдите их произведение. 2 4 64=512. Поскольку нужно найти результат среднего геометрического трех чисел, что из произведения извлеките корень третей степени. Сделать это устно затруднительно, поэтому воспользуйтесь инженерным калькулятором. Для этого в нем есть кнопка «x^y». Наберите число 512, нажмите кнопку «x^y», после чего наберите число 3 и нажмите кнопку «1/х», чтобы найти значение 1/3, нажмите кнопку «=». Получим результат возведения 512 в степень 1/3, что соответствует корню третьей степени. Получите 512^1/3=8. Это и есть среднее геометрическое чисел 2,4 и 64.

С помощью инженерного калькулятора можно найти среднее геометрическое другим способом. Найдите на клавиатуре кнопку log. После этого возьмите логарифм для каждого из чисел, найдите их сумму и поделите ее на количество чисел. Из полученного числа возьмите антилогарифм. Это и будет среднее геометрическое чисел. Например, для того чтобы найти среднее геометрическое тех же чисел 2, 4 и 64, сделайте на калькуляторе набор операций. Наберите число 2, после чего нажмите кнопку log, нажмите кнопку «+», наберите число 4 и снова нажмите log и «+», наберите 64, нажмите log и «=». Результатом будет число, равное сумме десятичных логарифмов чисел 2, 4 и 64. Полученное число разделите на 3, поскольку это количество чисел, по которым ищется среднее геометрическое. Из результата возьмите антилогарифм, переключив кнопку регистра, и используйте ту же клавишу log. В результате получится число 8, это и есть искомое среднее геометрическое.

В большинстве случаев данные концентрируются вокруг некоей центральной точки. Таким образом, чтобы описать любой набор данных, достаточно указать средне значение. Рассмотрим последовательно три числовые характеристики, которые используются для оценки среднего значения распределения: среднее арифметическое, медиана и мода.

Среднее арифметическое

Среднее арифметическое (часто называемое просто средним) — наиболее распространенная оценка среднего значения распределения. Она является результатом деления суммы всех наблюдаемых числовых величин на их количество. Для выборки, состоящей из чисел Х 1 , Х 2 , …, Х
n
, выборочное среднее (обозначаемое символом
) равно = (Х 1 + Х 2 + … + Х
n
) /
n
,
или

где — выборочное среднее, n
— объем выборки, X
i
– i-й элемент выборки.

Скачать заметку в формате или , примеры в формате

Рассмотрим вычисление среднего арифметического значения пятилетней среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска (рис. 1).

Рис. 1. Среднегодовая доходность 15 взаимных фондов с очень высоким уровнем риска

Выборочное среднее вычисляется следующим образом:

Это хороший доход, особенно по сравнению с 3–4% дохода, который получили вкладчики банков или кредитных союзов за тот же период времени. Если упорядочить значения доходности, то легко заметить, что восемь фондов имеют доходность выше, а семь — ниже среднего значения. Среднее арифметическое играет роль точки равновесия, так что фонды с низкими доходами уравновешивают фонды с высокими доходами. В вычислении среднего задействованы все элементы выборки. Ни одна из других оценок среднего значения распределения не обладает этим свойством.

Когда следует вычислять среднее арифметическое.
Поскольку среднее арифметическое зависит от всех элементов выборки, наличие экстремальных значений значительно влияет на результат. В таких ситуациях среднее арифметическое может исказить смысл числовых данных. Следовательно, описывая набор данных, содержащий экстремальные значения, необходимо указывать медиану либо среднее арифметическое и медиану. Например, если удалить из выборки доходность фонда RS Emerging Growth, выборочное среднее доходности 14 фондов уменьшится почти на 1% и составит 5,19%.

Медиана

Медиана представляет собой срединное значение упорядоченного массива чисел. Если массив не содержит повторяющихся чисел, то половина его элементов окажется меньше, а половина — больше медианы. Если выборка содержит экстремальные значения, для оценки среднего значения лучше использовать не среднее арифметическое, а медиану. Чтобы вычислить медиану выборки, ее сначала необходимо упорядочить.

Эта формула неоднозначна. Ее результат зависит от четности или нечетности числа n
:

Если выборка содержит нечетное количество элементов, медиана равна (n+1)/2
-му элементу.
Если выборка содержит четное количество элементов, медиана лежит между двумя средними элементами выборки и равна среднему арифметическому, вычисленному по этим двум элементам.

Чтобы вычислить медиану выборки, содержащей данные о доходности 15 взаимных фондов с очень высокий уровнем риска, сначала необходимо упорядочить исходные данные (рис. 2). Тогда медиана будет напротив номера среднего элемента выборки; в нашем примере №8. В Excel есть специальная функция =МЕДИАНА(), которая работает и с неупорядоченными массивами тоже.

Рис. 2. Медиана 15 фондов

Таким образом, медиана равна 6,5. Это означает, что доходность одной половины фондов с очень высоким уровнем риска не превышает 6,5, а доходность второй половины — превышает ее. Обратите внимание на то, что медиана, равная 6,5, ненамного больше среднего значения, равного 6,08.

Если удалить из выборки доходность фонда RS Emerging Growth, то медиана оставшихся 14 фондов уменьшится до 6,2%, то есть не так значительно, как среднее арифметическое (рис. 3).

Рис. 3. Медиана 14 фондов

Мода

Термин был впервые введен Пирсоном в 1894 г. Мода — это число, которое чаще других встречается в выборке (наиболее модное). Мода хорошо описывает, например, типичную реакцию водителей на сигнал светофора о прекращении движения. Классический пример использования моды — выбор размера выпускаемой партии обуви или цвета обоев. Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»). Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтение или отношение к чему-то, то мультимодальность может означать, что существуют несколько определенно различных мнений. Мультимодальность также служит индикатором того, что выборка не является однородной и наблюдения, возможно, порождены двумя или более «наложенными» распределениями. В отличие от среднего арифметического, выбросы на моду не влияют. Для непрерывно распределенных случайных величин, например, для показателей среднегодовой доходности взаимных фондов, мода иногда вообще не существует (или не имеет смысла). Поскольку эти показатели могут принимать самые разные значения, повторяющиеся величины встречаются крайне редко.

Квартили

Квартили — это показатели, которые чаще всего используются для оценки распределения данных при описании свойств больших числовых выборок. В то время как медиана разделяет упорядоченный массив пополам (50% элементов массива меньше медианы и 50% — больше), квартили разбивают упорядоченный набор данных на четыре части. Величины Q 1 , медиана и Q 3 являются 25-м, 50-м и 75-м перцентилем соответственно. Первый квартиль Q 1 — это число, разделяющее выборку на две части: 25% элементов меньше, а 75% — больше первого квартиля.

Третий квартиль Q 3 — это число, разделяющее выборку также на две части: 75% элементов меньше, а 25% — больше третьего квартиля.

Для расчета квартилей в версиях Excel до 2007 г. использовалась функция =КВАРТИЛЬ(массив;часть). Начиная с версии Excel2010 применяются две функции:

=КВАРТИЛЬ.ВКЛ(массив;часть)
=КВАРТИЛЬ.ИСКЛ(массив;часть)

Эти две функции дают немного различные значения (рис. 4). Например, при вычислении квартилей выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска Q 1 = 1,8 или –0,7 для КВАРТИЛЬ.ВКЛ и КВАРТИЛЬ.ИСКЛ, соответственно. Кстати функция КВАРТИЛЬ, использовавшаяся ранее соответствует современной функции КВАРТИЛЬ.ВКЛ. Для расчета квартилей в Excel с помощью вышеприведенных формул массив данных можно не упорядочивать.

Рис. 4. Вычисление квартилей в Excel

Подчеркнем еще раз. Excel умеет рассчитывать квартили для одномерного дискретного ряда
, содержащего значения случайной величины. Расчет квартилей для распределения на основе частот приведен ниже в разделе .

Среднее геометрическое

В отличие от среднего арифметического среднее геометрическое позволяет оценить степень изменения переменной с течением времени. Среднее геометрическое — это корень n
-й степени из произведения n
величин (в Excel используется функция =СРГЕОМ):

G
= (X 1 * X 2 * … * X n) 1/n

Похожий параметр – среднее геометрическое значение нормы прибыли – определяется формулой:

G = [(1 + R 1) * (1 + R 2) * … * (1 + R n)] 1/n – 1,

где R i
– норма прибыли за i
-й период времени.

Например, предположим, что объем вложенных средств в исходный момент времени равен 100 000 долл. К концу первого года он падает до уровня 50 000 долл., а к концу второго года восстанавливается до исходной отметки 100 000 долл. Норма прибыли этой инвестиции за двухлетний период равна 0, поскольку первоначальный и финальный объем средств равны между собой. Однако среднее арифметическое годовых норм прибыли равно = (–0,5 + 1) / 2 = 0,25 или 25%, поскольку норма прибыли в первый год R 1 = (50 000 – 100 000) / 100 000 = –0,5, а во второй R 2 = (100 000 – 50 000) / 50 000 = 1. В то же время, среднее геометрическое значение нормы прибыли за два года равно: G = [(1–0,5) * (1+1)] 1/2 – 1 = ½ – 1 = 1 – 1 = 0. Таким образом, среднее геометрическое точнее отражает изменение (точнее, отсутствие изменений) объема инвестиций за двухлетний период, чем среднее арифметическое.

Интересные факты.
Во-первых, среднее геометрическое всегда будет меньше среднего арифметического тех же чисел. За исключением случая, когда все взятые числа равны друг другу. Во-вторых, рассмотрев свойства прямоугольного треугольника, можно понять, почему среднее называется геометрическим. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу, а каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу (рис. 5). Это даёт геометрический способ построения среднего геометрического двух (длин) отрезков: нужно построить окружность на сумме этих двух отрезков как на диаметре, тогда высота, восставленная из точки их соединения до пересечения с окружностью, даст искомую величину:

Рис. 5. Геометрическая природа среднего геометрического (рисунок из Википедии)

Второе важное свойство числовых данных — их вариация
, характеризующая степень дисперсии данных. Две разные выборки могут отличаться как средними значениями, так и вариациями. Однако, как показано на рис. 6 и 7, две выборки могут иметь одинаковые вариации, но разные средние значения, либо одинаковые средние значения и совершенно разные вариации. Данные, которым соответствует полигон В на рис. 7, изменяются намного меньше, чем данные, по которым построен полигон А.

Рис. 6. Два симметричных распределения колоколообразной формы с одинаковым разбросом и разными средними значениями

Рис. 7. Два симметричных распределения колоколообразной формы с одинаковыми средними значениями и разным разбросом

Существует пять оценок вариации данных:

размах,
межквартильный размах,
дисперсия,
стандартное отклонение,
коэффициент вариации.

Размах

Размахом называется разность между наибольшим и наименьшим элементами выборки:

Размах = Х
Max – Х
Min

Размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, можно вычислить, используя упорядоченный массив (см. рис. 4): Размах = 18,5 – (–6,1) = 24,6. Это значит, что разница между наибольшей и наименьшей среднегодовой доходностью фондов с очень высоким уровнем риска равна 24,6% .

Размах позволяет измерить общий разброс данных. Хотя размах выборки является весьма простой оценкой общего разброса данных, его слабость заключается в том, что он никак не учитывает, как именно распределены данные между минимальным и максимальным элементами. Этот эффект хорошо прослеживается на рис. 8, который иллюстрирует выборки, имеющие одинаковый размах. Шкала В демонстрирует, что если выборка содержит хотя бы одно экстремальное значение, размах выборки оказывается весьма неточной оценкой разброса данных.

Рис. 8. Сравнение трех выборок, имеющих одинаковый размах; треугольник символизирует опору весов, и его расположение соответствует среднему значению выборки

Межквартильный размах

Межквартильный, или средний, размах — это разность между третьим и первым квартилями выборки:

Межквартильный размах = Q 3 – Q 1

Эта величина позволяет оценить разброс 50% элементов и не учитывать влияние экстремальных элементов. Межквартильный размах выборки, содержащей данные о среднегодовой доходности 15 взаимных фондов с очень высоким уровнем риска, можно вычислить, используя данные на рис. 4 (например, для функции КВАРТИЛЬ.ИСКЛ): Межквартильный размах = 9,8 – (–0,7) = 10,5. Интервал, ограниченный числами 9,8 и –0,7, часто называют средней половиной.

Следует отметить, что величины Q 1 и Q 3 , а значит, и межквартильный размах, не зависят от наличия выбросов, поскольку при их вычислении не учитывается ни одна величина, которая была бы меньше Q 1 или больше Q 3 . Суммарные количественные характеристики, такие как медиана, первый и третий квартили, а также межквартильный размах, на которые не влияют выбросы, называются устойчивыми показателями.

Хотя размах и межквартильный размах позволяют оценить общий и средний разброс выборки соответственно, ни одна из этих оценок не учитывает, как именно распределены данные. Дисперсия и стандартное отклонение
лишены этого недостатка. Эти показатели позволяют оценить степень колебания данных вокруг среднего значения. Выборочная дисперсия
является приближением среднего арифметического, вычисленного на основе квадратов разностей между каждым элементом выборки и выборочным средним. Для выборки Х 1 , Х 2 , … Х n выборочная дисперсия (обозначаемая символом S 2 задается следующей формулой:

В общем случае выборочная дисперсия — это сумма квадратов разностей между элементами выборки и выборочным средним, деленная на величину, равную объему выборки минус один:

где
— арифметическое среднее, n
— объем выборки, X i
— i
-й элемент выборки X
. В Excel до версии 2007 для расчета выборочной дисперсии использовалась функция =ДИСП(), с версии 2010 используется функция =ДИСП.В().

Наиболее практичной и широко распространенной оценкой разброса данных является стандартное выборочное отклонение
. Этот показатель обозначается символом S и равен квадратному корню из выборочной дисперсии:

В Excel до версии 2007 для расчета стандартного выборочного отклонения использовалась функция =СТАНДОТКЛОН(), с версии 2010 используется функция =СТАНДОТКЛОН.В(). Для расчета этих функций массив данных может быть неупорядоченным.

Ни выборочная дисперсия, ни стандартное выборочное отклонение не могут быть отрицательными. Единственная ситуация, в которой показатели S 2 и S могут быть нулевыми, — если все элементы выборки равны между собой. В этом совершенно невероятном случае размах и межквартильный размах также равны нулю.

Числовые данные по своей природе изменчивы. Любая переменная может принимать множество разных значений. Например, разные взаимные фонды имеют разные показатели доходности и убытков. Вследствие изменчивости числовых данных очень важно изучать не только оценки среднего значения, которые по своей природе являются суммарными, но и оценки дисперсии, характеризующие разброс данных.

Дисперсия и стандартное отклонение позволяют оценить разброс данных вокруг среднего значения, иначе говоря, определить, сколько элементов выборки меньше среднего, а сколько — больше. Дисперсия обладает некоторыми ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения — квадратный процент, квадратный доллар, квадратный дюйм и т.п. Следовательно, естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерений — процентах дохода, долларах или дюймах.

Стандартное отклонение позволяет оценить величину колебаний элементов выборки вокруг среднего значения. Практически во всех ситуациях основное количество наблюдаемых величин лежит в интервале плюс-минус одно стандартное отклонение от среднего значения. Следовательно, зная среднее арифметическое элементов выборки и стандартное выборочное отклонение, можно определить интервал, которому принадлежит основная масса данных.

Стандартное отклонение доходности 15 взаимных фондов с очень высоким уровнем риска равно 6,6 (рис. 9). Это значит, что доходность основной массы фондов отличается от среднего значения не более чем на 6,6% (т.е. колеблется в интервале от – S
= 6,2 – 6,6 = –0,4 до + S
= 12,8). Фактически в этом интервале лежит пятилетняя среднегодовая доходность 53,3% (8 из 15) фондов.

Рис. 9. Стандартное выборочное отклонение

Обратите внимание на то, что в процессе суммирования квадратов разностей элементы выборки, лежащие дальше от среднего значения, приобретают больший вес, чем элементы, лежащие ближе. Это свойство является основной причиной того, что для оценки среднего значения распределения чаще всего используется среднее арифметическое значение.

Коэффициент вариации

В отличие от предыдущих оценок разброса, коэффициент вариации является относительной оценкой. Он всегда измеряется в процентах, а не в единицах измерения исходных данных. Коэффициент вариации, обозначаемый символами CV, измеряет рассеивание данных относительно среднего значения. Коэффициент вариации равен стандартному отклонению, деленному на среднее арифметическое и умноженному на 100%:

где S
— стандартное выборочное отклонение,
— выборочное среднее.

Коэффициент вариации позволяет сравнить две выборки, элементы которых выражаются в разных единицах измерения. Например, управляющий службы доставки корреспонденции намеревается обновить парк грузовиков. При погрузке пакетов следует учитывать два вида ограничений: вес (в фунтах) и объем (в кубических футах) каждого пакета. Предположим, что в выборке, содержащей 200 пакетов, средний вес равен 26,0 фунтов, стандартное отклонение веса 3,9 фунтов, средний объем пакета 8,8 кубических футов, а стандартное отклонение объема 2,2 кубических фута. Как сравнить разброс веса и объема пакетов?

Поскольку единицы измерения веса и объема отличаются друг от друга, управляющий должен сравнить относительный разброс этих величин. Коэффициент вариации веса равен CV W = 3,9 / 26,0 * 100% = 15%, а коэффициент вариации объема CV V = 2,2 / 8,8 * 100% = 25% . Таким образом, относительный разброс объема пакетов намного больше относительного разброса их веса.

Форма распределения

Третье важное свойство выборки — форма ее распределения. Это распределение может быть симметричным или асимметричным. Чтобы описать форму распределения, необходимо вычислить его среднее значение и медиану. Если эти два показателя совпадают, переменная считается симметрично распределенной. Если среднее значение переменной больше медианы, ее распределение имеет положительную асимметрию (рис. 10). Если медиана больше среднего значения, распределение переменной имеет отрицательную асимметрию. Положительная асимметрия возникает, когда среднее значение увеличивается до необычайно высоких значений. Отрицательная асимметрия возникает, когда среднее значение уменьшается до необычайно малых значений. Переменная является симметрично распределенной, если она не принимает никаких экстремальных значений ни в одном из направлений, так что большие и малые значения переменной уравновешивают друг друга.

Рис. 10. Три вида распределений

Данные, изображенные на шкале А, имеют отрицательную асимметрию. На этом рисунке виден длинный хвост и перекос влево, вызванные наличием необычно малых значений. Эти крайне малые величины смещают среднее значение влево, и оно становится меньше медианы. Данные, изображенные на шкале Б, распределены симметрично. Левая и правая половины распределения являются своими зеркальными отражениями. Большие и малые величины уравновешивают друг друга, а среднее значение и медиана равны между собой. Данные, изображенные на шкале В, имеют положительную асимметрию. На этом рисунке виден длинный хвост и перекос вправо, вызванные наличием необычайно высоких значений. Эти слишком большие величины смещают среднее значение вправо, и оно становится больше медианы.

В Excel описательные статистики можно получить с помощью надстройки Пакет анализа
. Пройдите по меню Данные
→ Анализ данных
, в открывшемся окне выберите строку Описательная статистика
и кликните Ok
. В окне Описательная статистика
обязательно укажите Входной интервал
(рис. 11). Если вы хотите увидеть описательные статистики на том же листе, что и исходные данные, выберите переключатель Выходной интервал
и укажите ячейку, куда следует поместить левый верхний угол выводимых статистик (в нашем примере $C$1). Если вы хотите вывести данные на новый лист или в новую книгу, достаточно просто выбрать соответствующий переключатель. Поставьте галочку напротив Итоговая статистика
. По желанию также можно выбрать Уровень сложности,
k-й наименьший и
k-й наибольший
.

Если на вкладе Данные
в области Анализ
у вас не отображается пиктограмма Анализ данных
, нужно предварительно установить надстройку Пакет анализа
(см., например, ).

Рис. 11. Описательные статистики пятилетней среднегодовой доходности фондов с очень высоким уровнями риска, вычисленные с помощью надстройки Анализ данных
программы Excel

Excel вычисляет целый ряд статистик, рассмотренных выше: среднее, медиану, моду, стандартное отклонение, дисперсию, размах (интервал
), минимум, максимум и объем выборки (счет
). Кроме того, Excel вычисляет некоторые новые для нас статистики: стандартную ошибку, эксцесс и асимметричность. Стандартная ошибка
равна стандартному отклонению, деленному на квадратный корень объема выборки. Асимметричность
характеризует отклонение от симметричности распределения и является функцией, зависящей от куба разностей между элементами выборки и средним значением. Эксцесс представляет собой меру относительной концентрации данных вокруг среднего значения по сравнению с хвостами распределения и зависит от разностей между элементами выборки и средним значением, возведенных в четвертую степень.

Вычисление описательных статистик для генеральной совокупности

Среднее значение, разброс и форма распределения, рассмотренные выше, представляют собой характеристики, определяемые по выборке. Однако, если набор данных содержит числовые измерения всей генеральной совокупности, можно вычислить ее параметры. К числу таких параметров относятся математическое ожидание, дисперсия и стандартное отклонение генеральной совокупности.

Математическое ожидание
равно сумме всех значений генеральной совокупности, деленной на объем генеральной совокупности:

где µ
— математическое ожидание, X
i
— i
-е наблюдение переменной X
, N
— объем генеральной совокупности. В Excel для вычисления математического ожидания используется та же функция, что и для среднего арифметического: =СРЗНАЧ().

Дисперсия генеральной совокупности
равна сумме квадратов разностей между элементами генеральной совокупности и мат. ожиданием, деленной на объем генеральной совокупности:

где σ 2
– дисперсия генеральной совокупности. В Excel до версии 2007 для вычисления дисперсии генеральной совокупности используется функция =ДИСПР(), начиная с версии 2010 =ДИСП.Г().

Стандартное отклонение генеральной совокупности
равно квадратному корню, извлеченному из дисперсии генеральной совокупности:

В Excel до версии 2007 для вычисления стандартного отклонения генеральной совокупности используется функция =СТАНДОТКЛОНП(), начиная с версии 2010 =СТАНДОТКЛОН.Г(). Обратите внимание на то, что формулы для дисперсии и стандартного отклонения генеральной совокупности отличаются от формул для вычисления выборочной дисперсии и стандартного отклонения. При вычислении выборочных статистик S 2
и S
знаменатель дроби равен n – 1
, а при вычислении параметров σ 2
и σ
— объему генеральной совокупности N
.

Эмпирическое правило

В большинстве ситуаций крупная доля наблюдений концентрируется вокруг медианы, образуя кластер. В наборах данных, имеющих положительную асимметрию, этот кластер расположен левее (т.е. ниже) математического ожидания, а в наборах, имеющих отрицательную асимметрию, этот кластер расположен правее (т.е. выше) математического ожидания. У симметричных данных математическое ожидание и медиана совпадают, а наблюдения концентрируются вокруг математического ожидания, формируя колоколообразное распределение. Если распределение не имеет ярко выраженной асимметрии, а данные концентрируются вокруг некоего центра тяжести, для оценки изменчивости можно применять эмпирическое правило, которое гласит: если данные имеют колоколообразное распределение, то приблизительно 68% наблюдений отстоят от математического ожидания не более чем на одно стандартное отклонение, приблизительно 95% наблюдений отстоят от математического ожидания не более чем на два стандартных отклонения и 99,7% наблюдений отстоят от математического ожидания не более чем на три стандартных отклонения.

Таким образом, стандартное отклонение, представляющее собой оценку среднего колебания вокруг математического ожидания, помогает понять, как распределены наблюдения, и идентифицировать выбросы. Из эмпирического правила следует, что для колоколообразных распределений лишь одно значение из двадцати отличается от математического ожидания больше, чем на два стандартных отклонения. Следовательно, значения, лежащие за пределами интервала µ ± 2σ
, можно считать выбросами. Кроме того, только три из 1000 наблюдений отличаются от математического ожидания больше чем на три стандартных отклонения. Таким образом, значения, лежащие за пределами интервала µ ± 3σ
практически всегда являются выбросами. Для распределений, имеющих сильную асимметрию или не имеющих колоколообразной формы, можно применять эмпирическое правило Бьенамэ-Чебышева.

Более ста лет назад математики Бьенамэ и Чебышев независимо друг от друга открыли полезное свойство стандартного отклонения. Они обнаружили, что для любого набора данных, независимо от формы распределения, процент наблюдений, лежащих на расстоянии не превышающем k
стандартных отклонений от математического ожидания, не меньше (1 – 1/
k 2)*100%
.

Например, если k
= 2, правило Бьенамэ-Чебышева гласит, что как минимум (1 – (1/2) 2) х 100% = 75% наблюдений должно лежать в интервале µ ± 2σ
. Это правило справедливо для любого k
, превышающего единицу. Правило Бьенамэ-Чебышева носит весьма общий характер и справедливо для распределений любого вида. Оно указывает минимальное количество наблюдений, расстояние от которых до математического ожидания не превышает заданной величины. Однако, если распределение имеет колоколообразную форму, эмпирическое правило более точно оценивает концентрацию данных вокруг математического ожидания.

Вычисление описательных статистик для распределения на основе частот

Если исходные данные недоступны, единственным источником информации становится распределение частот. В таких ситуациях можно вычислить приближенные значения количественных показателей распределения, таких как среднее арифметическое, стандартное отклонение, квартили.

Если выборочные данные представлены в виде распределения частот, приближенное значение среднего арифметического можно вычислить, предполагая, что все значения внутри каждого класса сосредоточены в средней точке класса:

где
— выборочное среднее, n
— количество наблюдений, или объем выборки, с
— количество классов в распределении частот, m j
— средняя точка j
-гo класса, f
j
— частота, соответствующая j
-му классу.

Для вычисления стандартного отклонения по распределению частот также предполагается, что все значения внутри каждого класса сосредоточены в средней точке класса.

Чтобы понять, как определяются квартили ряда на основе частот, рассмотрим расчет нижнего квартиля на основе данных за 2013 г. о распределении населения России по величине среднедушевых денежных доходов (рис. 12).

Рис. 12. Доля населения России со среднедушевыми денежными доходами в среднем за месяц, рублей

Для расчета первого квартиля интервального вариационного ряда можно воспользоваться формулой:

где Q1 – величина первого квартиля, хQ1 – нижняя граница интервала, содержащего первый квартиль (интервал определяется по накопленной частоте, первой превышающей 25%); i – величина интервала; Σf – сумма частот всей выборки; наверное, всегда равна 100%; SQ1–1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль; fQ1 – частота интервала, содержащего нижний квартиль. Формула для третьего квартиля отличается тем, что во всех местах вместо Q1 нужно использовать Q3, а вместо ¼ подставить ¾.

В нашем примере (рис. 12) нижний квартиль находится в интервале 7000,1 – 10 000, накопленная частота которого равна 26,4%. Нижняя граница этого интервала – 7000 руб., величина интервала – 3000 руб., накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль – 13,4%, частота интервала, содержащего нижний квартиль – 13,0%. Таким образом: Q1 = 7000 + 3000 * (¼ * 100 – 13,4) / 13 = 9677 руб.

Ловушки, связанные с описательными статистиками

В этой заметке мы рассмотрели, как описать набор данных с помощью различных статистик, оценивающих его среднее значение, разброс и вид распределения. Следующим этапом является анализ и интерпретация данных. До сих пор мы изучали объективные свойства данных, а теперь переходим к их субъективной трактовке. Исследователя подстерегают две ошибки: неверно выбранный предмет анализа и неправильная интерпретация результатов.

Анализ доходности 15 взаимных фондов с очень высоким уровнем риска является вполне беспристрастным. Он привел к совершенно объективным выводам: все взаимные фонды имеют разную доходность, разброс доходности фондов колеблется от –6,1 до 18,5, а средняя доходность равна 6,08. Объективность анализа данных обеспечивается правильным выбором суммарных количественных показателей распределения. Было рассмотрено несколько способов оценки среднего значения и разброса данных, указаны их преимущества и недостатки. Как же выбрать правильную статистику, обеспечивающую объективный и беспристрастный анализ? Если распределение данных имеет небольшую асимметрию, следует ли выбирать медиану, а не среднее арифметическое? Какой показатель более точно характеризует разброс данных: стандартное отклонение или размах? Следует ли указывать на положительную асимметрию распределения?

С другой стороны, интерпретация данных является субъективным процессом. Разные люди приходят к разным выводам, истолковывая одни и те же результаты. У каждого своя точка зрения. Кто-то считает суммарные показатели среднегодовой доходности 15 фондов с очень высоким уровнем риска хорошими и вполне доволен полученным доходом. Другим может показаться, что эти фонды имеют слишком низкую доходность. Таким образом, субъективность следует компенсировать честностью, нейтральностью и ясностью выводов.

Этические проблемы

Анализ данных неразрывно связан с этическими вопросами. Следует критически относиться к информации, распространяемой газетами, радио, телевидением и Интерентом. Со временем вы научитесь скептически относиться не только к результатам, но и к целям, предмету и объективности исследований. Лучше всего об этом сказал известный британский политик Бенджамин Дизраэли: «Существуют три вида лжи: ложь, наглая ложь и статистика».

Как было отмечено в заметке этические проблемы возникают при выборе результатов, которые следует привести в отчете. Следует публиковать как положительные, так и отрицательные результаты. Кроме того, делая доклад или письменный отчет, результаты необходимо излагать честно, нейтрально и объективно. Следует различать неудачную и нечестную презентации. Для этого необходимо определить, каковы были намерения докладчика. Иногда важную информацию докладчик пропускает по невежеству, а иногда — умышленно (например, если он применяет среднее арифметическое для оценки среднего значения явно асимметричных данных, чтобы получить желаемый результат). Нечестно также замалчивать результаты, которые не соответствуют точке зрения исследователя.

Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 178–209

Функция КВАРТИЛЬ оставлена для совмещения с более ранними версиями Excel

Каждый человек в современном мире, планируя взять кредит или делая запасы овощей на зиму, периодически сталкивает с таким понятием, как «средняя величина». Давайте узнаем: что это такое, какие ее виды и классы существуют и зачем она применяется в статистике и других дисциплинах.

Средняя величина — это что такое?

Подобное название (СВ) носит обобщенная характеристика совокупности однородных явлений, определяемая по какому-либо одному количественному варьируемому признаку.

Однако люди далекие, от столь заумных определений, понимают это понятие, как среднее количество чего-то. Например, прежде чем взять кредит, сотрудник банка обязательно попросит потенциального клиента предоставить данные о среднем доходе за год, то есть общую сумму зарабатываемых человеком средств. Она вычисляется путем суммирования заработанного за весь год и разделения на количество месяцев. Таким образом, банк сможет определить, сумеет ли его клиент отдать долг в срок.

Зачем она используется?

Как правило, средние величины широко применяются для того, чтобы дать итоговую характеристику определенных общественных явлений, носящих массовый характер. Также они могут быть использованы для менее масштабных расчетов, как в случае с кредитом, в приведенном выше примере.

Однако чаще всего средние величины все же применяются для глобальных целей. В качестве примера одного из них можно привести вычисление количества потребляемой гражданами электроэнергии на протяжении одного календарного месяца. На основе полученных данных в дальнейшем устанавливаются максимальные нормы для категорий населения, пользующихся льготами от государства.

Также с помощью средних величин разрабатывается гарантийный срок службы тех или иных бытовых приборов, автомобилей, зданий и т. п. На основе собранных таким способом данных когда-то были разработаны современные нормы труда и отдыха.

Фактически любое явление современной жизни, носящее массовый характер, тем или иным образом обязательно связано с рассматриваемым понятием.

Сферы применения

Данное явление широко применяется практически во всех точных науках, особенно носящих экспериментальный характер.

Поиск среднего имеет огромное значение в медицине, инженерных дисциплинах, кулинарии, экономике, политике и т. п.

Основываясь на данных, полученных от подобных обобщений, разрабатывают лечебные препараты, учебные программы, устанавливают минимальные прожиточные минимумы и зарплаты, строят учебные графики, производят мебель, одежду и обувь, предметы гигиены и многое другое.

В математике данный термин именуется «средним значением» и применяется для осуществления решений различных примеров и задач. Наиболее простыми из них являются сложение и вычитание с обычными дробями. Ведь, как известно, для решения подобных примеров необходимо привести обе дроби к общему знаменателю.

Также в царице точных наук часто применяется близкий по смыслу термин «значение среднее случайной величины». Большинству он более знаком как «математическое ожидание», чаще рассматриваемое в теории вероятности. Стоит отметить, что подобное явление также применяется и при произведении статистических вычислений.

Средняя величина в статистике

Однако чаще всего изучаемое понятие используется в статистике. Как известно, эта наука сама по себе специализируется на вычислении и анализе количественной характеристики массовых общественных явлений. Поэтому средняя величина в статистике используется в качестве специализированного метода достижения ее основных задач — сбора и анализа информации.

Суть данного статистического метода заключается в замене индивидуальных уникальных значений рассматриваемого признака определенной уравновешенной средней величиной.

В качестве примера можно привести знаменитую шутку о еде. Итак, на неком заводе по вторникам на обед его начальство обычно ест мясную запеканку, а простые рабочие — тушеную капусту. На основе этих данных можно сделать вывод, что в среднем коллектив завода по вторникам обедает голубцами.

Хотя данный пример слегка утрирован, однако он иллюстрирует главный недостаток метода поиска средней величины — нивелирование индивидуальных особенностей предметов или личностей.

В средних величин применяются не только для анализа собранной информации, но и для планирования и прогнозирования дальнейших действий.

Также с его помощью производится оценка достигнутых результатов (например, выполнение плана по выращиванию и сбору урожая пшеницы за весенне-летний сезон).

Как правильно рассчитать

Хотя в зависимости от вида СВ существуют разные формулы ее вычисления, в общей теории статистики, как правило, применяется всего один способ расчета средней величины признака. Для этого нужно сначала сложить вместе значения всех явлений, а затем разделить получившуюся сумму на их количество.

При произведении подобных вычислений стоит помнить, что средняя величина всегда имеет ту же размерность (или единицы измерения), что и отдельная единица совокупности.

Условия правильного вычисления

Рассмотренная выше формула весьма проста и универсальна, так что ошибиться в ней практически невозможно. Однако всегда стоит учитывать два аспекта, иначе полученные данные не будут отражать реальную ситуацию.

Классы СВ

Найдя ответы на основные вопросы: «Средняя величина — это что такое?», «Где применяется она?» и «Как можно вычислить ее?», стоит узнать, какие классы и виды СВ существуют.

Прежде всего это явление делится на 2 класса. Это структурные и степенные средние величины.

Виды степенных СВ

Каждый из вышеперечисленных классов, в свою очередь, делится на виды. У степенного класса их четыре.

Средняя арифметическая величина — это наиболее распространенный вид СВ. Она являет собою среднее слагаемое, при определении коего общий объем рассматриваемого признака в совокупности данных поровну распределяется между всеми единицами данной совокупности.
Этот вид делится на подвиды: простая и взвешенная арифметическая СВ.
Средняя гармоническая величина — это показатель, обратный средней арифметической простой, вычисляемый из обратных значений рассматриваемого признака.
Она применяется в тех случаях, когда известны индивидуальные значения признака и произведение, а данные частоты — нет.
Средняя геометрическая величина чаще всего применима при анализе темпов роста экономических явлений. Она дает возможность сохранять в неизменном виде произведение индивидуальных значений данной величины, а не сумму.
Также бывает простой и взвешенной.
Средняя квадратическая величина используется при расчете отдельных показателе показателей, таких как коэффициент вариации, характеризующего ритмичность выпуска продукции и т. п.
Также с ее помощью вычисляются средние диаметры труб, колес, средние стороны квадрата и подобных фигур.

Как и все остальные виды средних СВ, среднеквадратическая бывает простой и взвешенной.

Виды структурных величин

Помимо средних СВ, в статистике довольно часто используются структурные виды. Они лучше подходят для расчета относительных характеристик величин варьирующего признака и внутреннего строения рядов распределения.

Таких видов существует два.

Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака. Для выяснения сущности средней величины необходимо рассмотреть особенности формирования значений признаков тех явлений, по данным которых исчисляют среднюю величину.

Известно, что единицы каждого массового явления обладают многочисленными признаками. Какой бы из этих признаков мы ни взяли, его значения у отдельных единиц будут различными, они изменяются, или, как говорят в статистике , варьируют от одной единицы к другой. Так, например, заработная плата работника определяется его квалификацией, характером труда, стажем работы и целым рядом других факторов, поэтому изменяется в весьма широких пределах. Совокупное влияние всех факторов определяет размер заработка каждого работника, тем не менее можно говорить о среднемесячной заработной плате работников разных отраслей экономики . Здесь мы оперируем типичным, характерным значением варьирующего признака, отнесенным к единице многочисленной совокупности.

Средняя величина отражает то общее,
что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень (или размер) любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное
для всех единиц изучаемой совокупности, которое и отражается в средней величине. Другие являются индивидуальными,
их действие выражено слабее и носит эпизодический, случайный характер. Они действуют в обратном направлении, обусловливают различия между количественными признаками отдельных единиц совокупности, стремясь изменить постоянную величину изучаемых признаков. Действие индивидуальных признаков погашается в средней величине. В совокупном влиянии типичных и индивидуальных факторов, которое уравновешивается и взаимно погашается в обобщающих характеристиках, проявляется в общем виде известный из математической статистики фундаментальный закон больших чисел.

В совокупности индивидуальные значения признаков сливаются в общую массу и как бы растворяются. Отсюда и средняя величина
выступает как «обезличенная», которая может отклоняться от индивидуальных значений признаков, не совпадая количественно ни с одним из них. Средняя величина отражает общее, характерное и типичное для всей совокупности благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц, так как ее величина определяется как бы общей равнодействующей из всех причин.

Однако для того, чтобы средняя величина отражала наиболее типичное значение признака, она должна определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений. Следовательно, средняя величина — это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.

Определяя, таким образом, сущность средних величин, необходимо подчеркнуть, что правильное исчисление любой средней величины предполагает выполнение следующих требований:

качественная однородность совокупности, по которой вычислена средняя величина. Это означает, что исчисление средних величин должно основываться на методе группировок, обеспечивающем выделение однородных, однотипных явлений;
исключение влияния на вычисление средней величины случайных, сугубо индивидуальных причин и факторов. Это достигается в том случае, когда вычисление средней основывается на достаточно массовом материале, в котором проявляется действие закона больших чисел, и все случайности взаимно погашаются;
при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показа-телъ
(свойство), на который она должна быть ориентирована.

Определяющий показатель может выступать в виде суммы значений осредняемого признака, суммы его обратных значений, произведения его значений и т. п. Связь между определяющим показателем и средней величиной выражается в следующем: если все значения осредняемого признака заменить средним значением, то их сумма или произведение в этом случае не изменит определяющего показателя. На основе этой связи определяющего показателя со средней величиной строят исходное количественное отношение для непосредственного расчета средней величины. Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.

Средняя величина, рассчитанная в целом по совокупности, называется общей средней;
средние величины, рассчитанные для каждой группы, — групповыми средними.
Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику явления, складывающуюся в конкретных условиях данной группы.

Способы расчета могут быть разные, поэтому в статистике различают несколько видов средней величины, основными из которых являются средняя арифметическая, средняя гармоническая и средняя геометрическая.

В экономическом анализе использование средних величин является основным инструментом для оценки результатов научно-технического прогресса, социальных мероприятий, поиска резервов развития экономики. В то же время следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении экономико-статистического анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.

Виды средних величин

В статистике используют различные виды средних величин, которые делятся на два больших класса:

степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадра-тическая, средняя кубическая);
структурные средние (мода, медиана).

Самый распространенный вид средней величины — средняя арифметическая. Под средней арифметической
понимается такое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. Вычисление данной величины сводится к суммированию всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности. Например, пять рабочих выполняли заказ на изготовление деталей, при этом первый изготовил 5 деталей, второй — 7, третий — 4, четвертый — 10, пятый- 12. Поскольку в исходных данных значение каждого варианта встречалось только один раз, для определения средней выработки одного рабочего следует применить формулу простой средней арифметической:

т. е. в нашем примере средняя выработка одного рабочего равна

Наряду с простой средней арифметической изучают среднюю арифметическую взвешенную.
Например, рассчитаем средний возраст студентов в группе из 20 человек , возраст которых варьируется от 18 до 22 лет, где xi
— варианты осредняемого признака, fi
— частота, которая показывает, сколько раз встречается i-е
значение в совокупности (табл. 5.1).

Таблица 5.1

Средний возраст студентов

Применяя формулу средней арифметической взвешенной, получаем:

В некоторых случаях характер исходных статистических данных таков, что расчет средней арифметической теряет смысл и единственным обобщающим показателем может служить только другой вид средней величины — средняя гармоническая.
В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность при расчете обобщающих статистических показателей в связи с повсеместным внедрением электронно-вычислительной техники. Большое практическое значение приобрела средняя гармоническая величина, которая тоже бывает простой и взвешенной. Если известны численные значения числителя логической формулы, а значения знаменателя неизвестны, но могут быть найдены как частное деление одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной.

Например, пусть известно, что автомобиль прошел первые 210 км со скоростью 70 км/ч, а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость автомобиля на протяжении всего пути в 360 км, используя формулу средней арифметической, нельзя. Так как вариантами являются скорости на отдельных участках xj
= 70 км/ч и Х2
= 75 км/ч, а весами (fi) считаются соответствующие отрезки пути, то произведения вариантов на веса не будут иметь ни физического, ни экономического смысла. В данном случае смысл приобретают частные от деления отрезков пути на соответствующие скорости (варианты xi), т. е. затраты времени на прохождение отдельных участков пути (fi/
xi). Если отрезки пути обозначить через fi, то весь путь выразиться как Σfi, а время, затраченное на весь путь, — как Σ fi/
xi ,
Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени:

В нашем примере получим:

где xi — отдельные варианты; n
— число вариантов осредняемого признака. В примере со скоростью простую среднюю гармоническую можно было бы применить, если бы были равны отрезки пути, пройденные с разной скоростью.

Таблица 5.2

Формула средней геометрической взвешенной
имеет следующий вид:

Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая — при абсолютных значениях уровней ряда.

Средняя квадратическая взвешенная
рассчитывается по другой формуле:

Средняя кубическая
применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

где — средняя величина; — индивидуальное значение; n
— число единиц изучаемой совокупности; k
— показатель степени, определяющий вид средней.

Мода
— величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда, т. е. вариант, обладающий наибольшей частотой. Мода может применяться при определении магазинов, которые чаще посещаются, наиболее распространенной цены на какой-либо товар. Она показывает размер признака, свойственный значительной части совокупности, и определяется по формуле

где х0 — нижняя граница интервала; h
— величина интервала; fm
— частота интервала; fm_
1 — частота предшествующего интервала; fm+
1 — частота следующего интервала.

Медианой
называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой — больше ее. Медиана используется при изучении элемента, значение которого больше или равно или одновременно меньше или равно половине элементов ряда распределения. Медиана дает общее представление о том, где сосредоточены значения признака, иными словами, где находится их центр.

где X0
— нижняя граница интервала; h
— величина интервала; fm
— частота интервала; f
— число членов ряда;

∫m-1 — сумма накопленных членов ряда, предшествующих данному.

Наряду с медианой для более полной характеристики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относятся квартили
и децили.
Квартили делят ряд по сумме частот на 4 равные части, а децили — на 10 равных частей. Квартилей насчитывается три, а децилей — девять.

Показатели вариации

Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения.
Различают два типа рядов распределения — атрибутивные и вариационные, в зависимости от того, является ли признак, взятый за основу группировки, качественным или количественным.

Вариационными
называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности не постоянны, более или менее различаются между собой. Такое различие в величине признака носит название вариации.
Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений.
Наличие вариации у отдельных единиц совокупности обусловлено влиянием большого числа факторов на формирование уровня признака. Изучение характера и степени вариации признаков у отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Для описания меры изменчивости признаков используют показатели вариации.

Другой важной задачей статистического исследования является определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности. Для решения такой задачи в статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых измеряется вариация. В практике исследователь сталкивается с достаточно большим количеством вариантов значений признака, что не дает представления о распределении единиц по величине признака в совокупности. Для этого проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда.
Ранжированный ряд сразу дает общее представление о значениях, которые принимает признак в совокупности.

Недостаточность средней величины для исчерпывающей характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака. Использование этих показателей вариации дает возможность сделать статистический анализ более полным и содержательным и тем самым глубже понять сущность изучаемых общественных явлений.

Самыми простыми признаками вариации являются минимум
и максимум —
это наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения.
Обозначим частоту повторения значения признака fi,
сумма частот, равная объему изучаемой совокупности будет:

где k
— число вариантов значений признака. Частоты удобно заменять частостями — wi. Частость
— относительный показатель частоты — может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Формально имеем:

Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся среднее линейное отклонение, размах вариации, дисперсия, среднее квадратическое отклонение.

Размах вариации
(R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: R
= Xmax — Xmin. Этот показатель дает лишь самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Он совершенно не связан с частотами в вариационном ряду, т. е. с характером распределения, а его зависимость может придавать ему неустойчивый, случайный характер только от крайних значений признака. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних величин. Область применения этого показателя ограничена достаточно однородными совокупностями, точнее, характеризует вариацию признака показатель, основанный на учете изменчивости всех значений признака.

Для характеристики вариации признака нужно обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины. Такие показатели

вариации, как среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение
представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

Абсолютное значение (модуль) отклонения варианта от средней арифметической; f-
частота.

Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая — в рядах с неравными частотами.

Существует и другой способ усреднения отклонений вариантов от средней арифметической. Этот очень распространенный в статистике способ сводится к расчету квадратов отклонений вариантов от средней величины с их последующим усреднением. При этом мы получаем новый показатель вариации — дисперсию.

Дисперсия
(σ 2) — средняя из квадратов отклонений вариантов значений признака от их средней величины:

Вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).

В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение
(σ) представляет собой корень квадратный из дисперсии:

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражаются в тех же единицах измерения, что и варианты.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, большой интерес представляет сравнение вариаций возраста персонала и его квалификации, стажа работы и размера заработной платы и т. д. Для подобных сопоставлений показатели абсолютной колеблемости признаков — среднее линейное и среднее квадртическое отклонение — не пригодны. Нельзя, в самом деле, сравнивать колеблемость стажа работы, выражаемую в годах, с колеблемостью заработной платы, выражаемой в рублях и копейках.

При сравнении изменчивости различных признаков в совокупности удобно применять относительные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости:

Наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному.

Источник

Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Например: найдем среднее арифметическое чисел 2; 6; 9; 15.

У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Например: найдем размах чисел 2; 5; 8; 12; 33.

Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.

Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.

Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.

Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.

В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.

Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите медиану и размах ряда.
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

Найдите моду ряда и среднее арифметическое ряда.
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.

Найдите среднюю заработную плату.
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.

Найдите разность среднего арифметического и медианы этого набора.
Найдите объем и медиану числового ряда.

9; 7; 1; 1; 11; 5; 1.
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:

I II III IV V VI VII

37 34 35 32 36 33 38

Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.

Найдите среднее арифметическое этого набора чисел.
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.

Найдите медиану этого набора чисел.
Провели несколько измерений случайной величины:

800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.

Найдите разность среднего арифметического и медианы этого набора.
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.

Найдите среднее арифметическое, размах и моду.

I	II	III	IV	V	VI	VII
37	34	35	32	36	33	38

Источник

ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ

Тема
4. СРЕДНИЕ ВЕЛИЧИНЫ

4.1.
Средние показатели

Средняя величина есть обобщающая количественная характеристика
совокупности однотипных явлений по одному варьирующему признаку.

Она отражает определённый уровень достигнутый в процессе развития
явления к определённому периоду или моменту времени.

Средняя величина – абстрактная величина. Поэтому анализ проводимый при
ней всегда дополняется показом индивидуальных величин.

Среднее может быть вычислено только для какой-то однородной
совокупности.

Расчёт средней необходимо сочетать с группировкой.

В статистике рассчитывают индивидуальные и общие средние.

Общее среднее затушёвывает существенные (существующие) отличия между
явлениями таким образом во многих случаях они становятся фиктивными.

Признак по которым находится среднее
называется усредняемое (Х). Величина усредняемого признака у каждой единицы
совокупности называется индивидуальное значение.

Значение признака, которое встречается у
крупных единиц или отдельных единиц и не повторяется называется вариантами
признака (Х1, Х2, …).

Средняя арифметическая.

Средняя
арифметическая простая (рассчитывается по несгруппированным данным):

. ,

где x₁ ,x₂, …, x_n-значение признака (варианты), n— число вариантов.

Средняя арифметическая взвешенная (рассчитывается
по сгруппированным данным):

где f₁, f₂, …, f_n — веса
(частоты) значений признака.

f— частота повторения соответствующих вариантов в статистике называется
весом.

Пример: 1) Вычислить средний возраст выпуска, возраст
которого: 24,22,25,24,25,24,22,22,24,26 лет.

Расчёт по средней арифметической простой:

2)
Расчёт по средней
арифметической взвешенной.

Возраст (х)

Число выпускников (f)

Сумма возрастов (хf)

Сумма

238

Свойства средней арифметической:

1)
Сумма отклонений
значений признака от средней арифметической равно 0.

2)
Если от каждого
варианта вычесть или к каждому варианту прибавить какое-либо постоянное число,
то среднее увеличится или уменьшится на то же самое число.

3)
Если каждый вариант
умножить или разделить на какое-либо число, то среднее уменьшится или
увеличится во столько же раз.

4)
Если веса или частоты
разделить или умножить на какое-либо число, то величина средней не изменится.

Это свойство даёт возможность частоты заменять их удельными весами

где р – удельный вес, выраженный в процентах.

Если удельный вес выражается в доле, то

Средняя гармоническая.

Рассчитывается, когда 1) среднее арифметическое по
имеющимся данным рассчитать невозможно, 2) расчет средней гармонической более
удобен.

Средняя гармоническая простая: .

Средняя гармоническая взвешенная: .

Пример: требуется вычислить
производительность труда рабочей силы, если первому рабочему требуется для
изготовления единицы продукции 0,25 часа, второму – 1/3 часа, третьему – 1/2
часа.

Средняя геометрическая.

Средняя геометрическая простая:

Средняя геометрическая взвешенная:

Наиболее широкое применение этот вид средней получил в анализе динамики
для определения среднего темпа роста.

Средняя квадратическая.

Средняя квадратическая простая:

Средняя квадратическая взвешенная:

Пример: Оценка за ответ на первый вопрос – 2, на
второй вопрос – 5.

4.2.
Структурные средние

Для того чтобы определить среднее в некоторых случаях нет
необходимости, или возможности прибегать к расчёту степенных средних в этих
случаях появляется возможность или необходимость расчёта структурной средней.

Если величина средней (ср. арифметической) зависит от всех значений
признака, встречаемых в данном распределении, то значение структурной средней
определяется структурой распределения, местом распределения. Отсюда их
названия.

Медиана – значение признака, приходящееся на
середину ранжированной (упорядоченной) совокупности. Медиана делит совокупность
на две равные части.

Медиана в интервальном ряду рассчитывается следующим образом:

Для определения медианы прежде всего исчисляют её порядковый номер по
формуле

или

(для интервальных
рядов) и строят ряд накопленных частот. Накопленной частоте, которая равна
порядковому номеру медианы или первая его превышает, в дискретном вариационном
ряду соответствует вариант, являющийся медианой, а в интервальном вариационном
ряду – медианный интервал.

где Х₀ – нижняя граница медианного
интервала,

d – величина медианного интервала,

f_i – частота i-го интервала,

S_ме-1
– сумма накопленных весов по интервалу
предшествующему медианному,

f_Me
– частота медианного интервала.

Пример: Имеются
данные о з/п рабочих:

Месячная з/п (руб) х	Количество рабочих, f_i	Накопленные частоты, S_i
До 800	1	1
800- 1000	2	3
1000- 1200	4	7
1200- 1400	1	8
1400 и более	2	10
Итого	10

Мода – значение признака, которое чаще других
встречается в данном ряду распределения.

Мода для дискретного ряда определяется как варианта, имеющая
наибольшую частоту.

Для интервального ряда:

где Х₀ –нижняя граница модального
интервала,

d – величина модального интервала,

f_Mo_-1 – частота (вес) интервала,
предшествующего модальному,

f_Mo – частота (вес) модального интервала,

f_Mo₊₁ – частота (вес) интервала, следующего за модальным.

Пример: (См. предыдущую задачу)

Квартили – значения признака, делящие
ранжированную совокупность на четыре равновеликие части.

Рассчитывают 1-й и 3-й квартили.

X_Q₁ – нижняя граница интервала, содержащего
нижний квартиль (интервал определяется по накопленной частоте, первой
превышающей 25%),

d – величина интервала,

f_Q₁ – частота квартильного интервала,

S_Q₁_-1 – сумма накопленных частот в интервале, предшествующего квартильному.

Q₂=Мe.

обозначения
аналогичны 1-му квартилю с изменением на верхний.

Децили – варианты, делящие ранжированный ряд
на десять равных частей.

Вычисляются они по той же схеме, что и медиана, и квартили. Обычно
рассчитывают только первый и девятый децили:

Значения признака, делящие ряд на сто частей, называются перцентилями.

Расчёт средних всегда производится одновременно с
количественным анализом, изучаемых совокупностей, средние величины
рассчитываются не всегда, когда на лицо количественная вариация признаков.

Средняя величина должна быть рассчитываема для количественно-однородной
совокупности.

Это требование состоит в том, что среднее нельзя применить к таким
совокупностям, отдельные части которых подчинены различным законам развития
относительных величин признака.

Тема 5. ПОКАЗАТЕЛИ
ВАРИАЦИИ

5.1.
Меры вариации

Колеблемость, многообразие, изменяемость величины признака у единиц
совокупности называются вариацией.

Вариация существует в пространстве и во времени.

Вариация в пространстве – колеблемость значений
признака по отдельным территориям.

Вариация во времени – изменение значений признака в
различные периоды (или моменты) времени.

Для измерения вариации используются такие показатели,
как размах вариации, среднее линейное отклонение, дисперсия, среднее
квадратическое отклонение, коэффициент вариации.

Простейший показатель – размах вариации.

R=X_max – X_min.

Из приведённой формы видно, что величина этого показателя целиком
зависит от случайности расположения крайних членов ряда.

Его недостаток в том, что варьирование значения признака из основной
массы членов ряда не находит отражения в этом показателе. В то же время
колеблимость признака складывается из всех его значений.

Среднее линейное отклонение:

– простая,

– взвешенная.

Показывает в среднем отклонение вариантов признака от их средней
величины.

Дисперсия:

простая,

взвешенная.

—

Это средняя величина квадратов отклонений.

Среднее квадратическое отклонение:

Это обобщающая характеристика размеров вариации признака в
совокупности. Оно выражается в тех же единицах измерения, что и признак.

Для расчёта дисперсии в дискретном рядах используется следующая
формула.

где , .

Пример: Распределение коров колхозной фермы по
годовому удою молока и расчёт абсолютных показателей вариации.

Годовой удой молока от коровы тыс.кг. (Х_i)	Число коров, f_i	Средняя величина признака, сер. интерв.	Х_if_i	Х_i–Х	\|X_i–X\|f_i	(X_i–X)2	(X_i–X)2f_i
До-2	4	1,5	6	-1,3	5,2	1,69	6,76
2-3	2	2,5	5	-0,3	0,6	0,09	0,18
3-4	2	3,5	7	+0,7	1,4	0,49	0,98
4-5	1	4,5	4,5	+1,7	1,7	2,89	2,89
5 и более	1	5,5	5,6	+2,1	2,7	7,29	7,29
Итого	10		28		11,6		18,1

1) Находим среднюю арифметическую

2) Среднее линейное отклонение:

тыс.кг.

2)
Дисперсия

тыс.кг.

4) Среднее квадратическое отклонение:

тыс.кг.

Дисперсия обладает рядом свойств, некоторые из которых позволяют упростить
её вычисление.

1. Дисперсия постоянной величины равна 0

2. Если все варианты значений признака уменьшить на одно число то
дисперсия не изменится.

3. Если все варианты значений признака уменьшить (увеличить) в одно и тоже
число раз (в К раз), то дисперсия уменьшится (увеличится) в К2
раз.

Дисперсия и среднее квадратическое отклонение – наиболее широко
применяемые показатели вариации, т.к. они входят в большинство теорем теории
вероятности, которая служит фундаментом математической статистики.

Коэффициент вариации.

Он используется не только для сравнения оценки вариации, но и для
характеристики однородной совокупности.

Совокупность считается однородной если коэффициент вариации <=0,33.

В статистике наряду с показателем вариации количественного признака
определяется показатель вариации качественного или альтернативного
признака.

Альтернативными признаками являются признаки, которым
обладают одни единицы совокупности и не обладают другие.

При статистическом выражении колеблимости признака, наличие изучаемого
признака обозначается «1», а его отсутствие «0».

Доля вариантов обладающих изучаемым признаком обозначается р, а
доля вариантов не обладающих изучаемым признаком обозначается q.

Найдём среднее:

Дисперсия альтернативного признака:

Пример: имеется совокупность новорождённых –
205 человек, девочки – 100.

Доля девочек р=100/205=0,488

Доля мальчиков q =105/205=0,512

Дисперсия альт. призн.= 0,488·0,512= 0,2498

p+q не может быть >1

p·q не может быть >0.25

5.2. Виды дисперсий

Общая дисперсия измеряет вариацию признака во всей совокупности под
влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперсия отражает вариацию
изучаемого признака, которая возникает под влиянием признака фактора,
положенного в основу группировки. Она характеризует колеблимость групповых
(частных) средних около общей средней

где – среднее по определённой группе; n_i
– численность отдельных групп.

Внутригрупповая дисперсия отражает случайную
вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и
не зависящую от признака-фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий:

Правило сложения дисперсий:

Можно рассчитать относительные показатели.

1.
Эмпирический коэффициент детерминации

Он показывает долю (удельный вес) общей вариации изучаемого признака,
обусловленную вариацией группировочного признака.

2. Эмпирическое корреляционное отношение

Оно характеризует влияние признака, положенного в
основание группировки, на вариацию результативного признака. Чем больше это
число, тем больше зависимость результативного признака от факторов положенных
в основу группировки.

Пример:

Тип хозяйства	Посевная площадь тысяч гект.	Средняя урожайность	Среднее отклонение урожайности
1	300	20	2
2	100	10	2,5

1)
Находим среднюю урожайности по двум типах хозяйств

2)
Средняя из групп дисперсий

(22ּ300+2,52ּ100)/400=4,5625

3)
Определяем межгрупповую дисперсию

4)
Определяем общую дисперсию

Эти данные свидетельствуют о том, что фактор положенный в основу
группировки оказывает существенное влияние на среднюю урожайность.

Выбор знака: если вариация факторного и результативного признака идёт в
одном направлении, то берётся знак «+», а если нет, то «–», сам по себе знак не
характеризует тесноту связи. Помимо расчета общей дисперсии и её составных
частей по абсолютным данным можно производить расчёт дисперсии доли.

5.3.
Теоретическое распределение в анализе вариационных рядов

При анализе изучаемых явлений в совокупности с другими, аналогичными по
своей сущности, часто удается обнаружить закономерность, связанную с их
возникновением. Наиболее часто закономерности описывают с помощью нормального
распределения:

Чем больше случайных величин действует вместе, тем точнее подчиненность
закону нормального распределения.

Примеры нормального распределения: 1) распределение отклонений в
производственном процессе при нормальном уровне организации и технологии, 2)
распределение населения определенного возраста по размеру обуви и т.д.

Соответствие эмпирического распределения нормальному можно оценивать с
помощью особых статистических показателей – критериев согласия.

Критерий согласия Пирсона (хи-квадрат)

где f_э и f_т – эмпирические и теоретические частоты
соответственно.

Затем с помощью «хи-квадрат» и числа степеней свободы (n-1) находят по специальным таблицам вероятность .

При Р>0,5 считается, что эмпирическое и теоретическое распределения
близки, при 0,2<P<0,5 – удовлетворительное, в
остальных случаях – недостаточное.

Критерий Романовского (С)

где γ – число степеней свободы (число групп минус три).

При С<3 различие несущественно, эмпирическое распределение близкое к
нормальному.

Критерий Колмогорова (λ)

где D – максимальное значение разности между
накопленными эмпирическими и теоретическими частотами,

f_i – эмпирические частоты.

Далее по таблицам вероятностей определяем . Чем
ближе к 1, тем лучше.

Тема 6. ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ЯВЛЕНИЙ

6.1. Понятие рядов динамики

Изучение изменения различных явлений во времени – одна из важнейших
задач статистики. Решается эта задача путем составления и анализа так
называемых рядов динамики (иногда их также называют временными или
хронологическими рядами).

Динамика – процесс развития, движения
социально-экономических явлений во времени.

Ряды динамики – ряды изменяющихся во времени
значений статистического показателя, расположенных в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда и
периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени.

Обозначения:

y – уровни ряда,

t – моменты или периоды времени, к которым относятся уровни.

Ряды динамики, как правило, представляют в виде таблицы или графически.
При графическом изображении ряда динамики на оси абсцисс строится шкала времени
t, а на оси ординат – шкала уровней ряда у (арифметическая или иногда
логарифмическая).

Одна из первых задач изучения рядов динамики – выявить основную
тенденцию (закономерность) в изменении уровней ряда, именуемую трендом.
Закономерность в изменении уровней ряда в одних случаях проявляется довольно
наглядно, в других – может затушевываться колебаниями, вызванными случайными и
неслучайными причинами.

Виды рядов динамики.

В одних рядах уровни могут быть выражены абсолютными показателями, в
других – средними или относительными. В зависимости от вида показателей уровней
ряда ряды динамики также подразделяют на ряды абсолютных, относительных и
средних величин (показателей).

На основе рядов абсолютных величин образуются ряды динамики
относительных и средних величин, поэтому ряды абсолютных величин рассматривают
как исходные, а ряды относительных и средних величин — как производные.

Ряды относительных величин могут характеризовать: темпы роста (или
снижения) определенного показателя; изменение удельного веса того или иного
показателя в совокупности (например, удельного веса (доли) городского населения
или доли приватизированных предприятий в той или иной отрасли); изменение показателей
интенсивности отдельных явлений (например, производство продукции на душу
населения, уровень рождаемости и смертности на 1000 человек населения) и др.

Примерами рядов динамики средних величин служат данные о среднегодовой
численности занятых в экономике (или безработных), о средней заработной плате в
отдельных отраслях, о среднем размере пенсий, о средней урожайности отдельных
сельскохозяйственных культур и др.

Кроме того, уровни рядов динамики могут относиться к определенным
моментам времени (датам) или же периодам (интервалам). В соответствии с этим в
статистике различают моментные и интервальные ряды динамики

Моментным называется ряд, уровни которого характеризуют
значение показателя (явления) по состоянию на определенные моменты времени
(дату).

Интервальным называется ряд, уровни которого
характеризуют значение показателя, достигнутое за определенный период (интервал).

Отметим отличительную особенность интервальных рядов абсолютных
величин: их уровни можно дробить и складывать (суммировать). Так, зная добычу
угля по годам, можно разделить каждый уровень на 12 и получить новые данные – о
среднемесячной добыче угля за указанный период. Или же, суммируя данные о
численности родившихся по месяцам, можно получить численность родившихся за
год. Подобные действия с уровнями моментного ряда лишены смысла.

Суммируя уровни интервальных рядов абсолютных величин, можно строить
ряды с нарастающим итогом.

6.2.
Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно
изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в
абсолютном и относительном выражении.

Анализ скорости и интенсивности развития явления во времени
осуществляется с помощью статистических показателей, которые получаются в
результате сравнения уровней между собой. При этом сравниваемый уровень
называют отчетным, а уровень, с которым производят сравнение, – базисным.

Чтобы проследить за направлением и размером изменений уровней во
времени, для рядов динамики рассчитывают такие показатели, как:

—
абсолютные приросты (изменения) уровней;

—
темпы роста;

—
темпы прироста (снижения) уровней.

Абсолютный прирост (Δy) характеризует размер изменения
уровня ряда за определенный промежуток времени. Он рассчитывается как разность
между двумя уровнями ряда. Абсолютный прирост показывает, на сколько (в
единицах измерения показателей ряда) уровень одного периода больше или меньше
уровня какого-либо предшествующего периода, и, следовательно, может иметь знак
«+» (при увеличении уровней) или «–» (при уменьшении уровней).

Δ_yi=y_i– y_i-1, i=1..n.

В зависимости от базы сравнения абсолютные приросты могут
рассчитываться как цепные и как базисные.

Вычитая из каждого уровня предыдущий

Δ_у
= y_i– y_i_-1,

получаем
абсолютные изменения уровней ряда за отдельные периоды как цепные.

Вычитая
из каждого уровня начальный

Δ_у
= y_i– y₀,

получаем
накопленные итоги прироста (изменения) показателя с начала изучаемого периода,
т.е. абсолютные изменения рассчитываются как базисные.

Если значения цепных абсолютных изменений постоянны, то уровни ряда
изменяются равномерно. Если же абсолютные приросты от периода к периоду
возрастают (или убывают), то уровни изменяются ускоренно (или замедленно). В
этом случае рассчитывается показатель ускорения как разность между двумя
смежными цепными абсолютными приростами.

Абсолютное ускорение (Δ′) – показывает,
насколько данная скорость больше (меньше) предыдущей.

Δ′=Δy_i–Δy_i_-1

Наряду с абсолютными изменениями уровней ряда важно измерить также их
относительное изменение.

Темп роста (Т_р) – показатель интенсивности
изменения уровня ряда, относительный показатель, рассчитываемый как отношение
двух уровней ряда.

В зависимости от базы сравнения темпы роста могут рассчитываться как
цепные, когда каждый уровень сопоставляется с уровнем предыдущего периода, и
как базисные, когда все уровни сопоставляются с уровнем одного какого-то
периода, принятого за базу сравнения (часто это начальный уровень ряда). Соответственно,
цепные темпы роста характеризуют интенсивность изменения в каждом отдельном
периоде, а базисные – за отрезок времени, отделяющий данный уровень от
базисного.

Базисный темп роста:

Цепной темп роста:

Темпы роста как относительные величины могут выражаться в виде
коэффициентов, т.е. простого кратного отношения (если база сравнения
принимается за единицу), и в процентах (если база сравнения принимается за 100
единиц). Говоря о темпах, чаще всего имеют в виду отношение уровней в
процентах.

Выраженные в коэффициентах темпы роста показывают, во сколько раз
уровень данного периода больше уровня базы сравнения или какую часть его
составляет. При процентном выражении темп роста показывает, сколько процентов
составляет уровень данного периода по сравнению с уровнем базы сравнения.

Между цепными и базисными коэффициентами роста существует связь,
позволяющая при необходимости переходить от цепных к базисным и наоборот.

В частности:

—
произведение цепных коэффициентов роста равно
базисному;

—
результат деления двух базисных коэффициентов равен
цепному

Темп прироста (Т_пр) характеризует
относительную скорость изменения уровня ряда в единицу времени, это относительный
показатель, показывающий, на сколько процентов данный уровень больше (или
меньше) другого, принимаемого за базу сравнения. Показатель Т_пр
можно рассчитать двояко:

—
путем вычитания 100% из темпа роста (снижения),

—
как процентное отношение абсолютного прироста к
тому уровню, по сравнению с которым рассчитан абсолютный прирост.

Абсолютное значение одного процента прироста

Абсолютное значение 1% прироста равно одной сотой предыдущего уровня

Для базисных абсолютных приростов и темпов прироста расчет не имеет
смысла, так как при сравнении всех накопленных приростов с одним и тем же
первоначальным уровнем для всех периодов будет получаться одно и то же значение
1% прироста.

Каждый ряд динамики можно рассматривать как некую совокупность изменяющихся
во времени показателей, которые можно обобщать в виде средних величин. Такие
обобщенные (средние) показатели особенно необходимы при сравнении изменений
того или иного показателя в разные периоды, в разных странах и т. д.

Средний уровень
ряда динамики. Для разных видов
рядов динамики средний уровень рассчитывается различным образом.

Для моментного равноотстоящего ряда динамики по средней хронологической:

Для моментного ряда динамики с неравноотстоящими уровнями:

где t_i – длительность интервала времени
между уровнями.

Для интервального ряда с равноотстоящими уровнями:

Для интервального ряда с неравноотстоящими уровнями:

Средний абсолютный прирост

Средний темп роста

Средний темп прироста

При анализе динамики социально-экономических явлений необходимо
параллельно использовать показатели скорости и интенсивности изменения уровней.

6.3. Анализ основной тенденции в рядах динамики

Описание тенденции в ряду динамики производится с
помощью методов сглаживания. Методы сглаживания разделяются на две основные
группы:

1)
сглаживание или
механическое выравнивание отдельных членов ряда динамики с использованием
фактических значений соседних уровней;

2)
выравнивание с применением
кривой, проведенной между конкретными уровнями таким образом, чтобы она
отображала тенденцию, присущую ряду, и освободила его от незначительных
колебаний.

Метод усреднения по левой и правой половине. Ряд динамики разделяют на две части, находят
для каждой из них среднее арифметическое значение и проводят через полученные
точки линию тренда на графике.

Метод укрупнения интервалов. Производится укрупнение периодов времени, к которым
относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется
рядом месячного выпуска продукции.

Метод скользящей средней. Вычисляется средний уровень из определенного числа
первых по порядку уровней ряда, затем – начиная со второго, далее – с третьего
и т.д.

Алгоритм расчета скользящей средней:

1.
Определяем интервал
сглаживания, т.е. число входящих в него уровней m (m<n).

2.
Вычислить среднее значение
уровней, образующих интервал сглаживания, по формуле

где m – число уровней, входящих в интервал сглаживания,

i – порядковый номер уровня в интервале сглаживания,

p – при нечетном m равно: p=(m-1)/2.

При четном m проводят центрирование:
находят среднюю из двух смежных скользящих средних для отнесения полученного
уровня к определенной дате.

3. Сдвинуть интервал сглаживания на одну точку вправо, затем вычислить все
последующие сглаженные значения, производя одновременно сдвиги.

Пример:

Год

Центнеров с 1 га

Скользящие трехлетние суммы

Трехлетние скользящие средние

1982

1983

1984

1985

1986

1987

1988

1989

9,5

13,7

12,1

14,0

13,2

15,6

15,4

14,0

—

35,3

39,8

39,3

42,8

44,2

—

11,77

13,27

13,1

14,27

14,73

—

Тема
7. ИНДЕКСНЫЕ МЕТОДЫ

7.1. Понятие индексов

В статистике под индексами понимаются относительные
величины, выражающие изменение сложных экономических явлений во времени,
пространстве и по сравнению с планом. В связи с этим различают динамические
индексы, характеризующие изменения явлений во времени; индексы выполнения
плана и территориальные индексы.

Индексы относятся либо к элементам сложного экономического явления,
либо ко всему явлению в целом. Показатели характеризующие изменение более или
менее однородных объектов входящих в состав сложных явлений называются
индивидуальные индексы

Принятые обозначения:

Q, q – физический объём;

p – цена единицы товара;

z – себестоимость единицы продукции;

pq – стоимость продукции или товарооборот;

zq – издержки производства.

7.2. Индивидуальные и общие индексы

Индивидуальные индексы (i) – это обычные относительные величины.

Индивидуальный индекс объёма:

q0 – базисный период (пояснить);

q1 – текущий период (пояснить).

Индивидуальный индекс цены:

Индивидуальный индекс товарооборота:

Индекс как индивидуальный так и общий получает название по названию
индексированной величины. Индексы как индивидуальные так и общие обозначаются
либо в виде коэффициента, либо в виде процентов.

Явления общественные и социальные, изучаемые в экономике состоят из
несопоставимых элементов. Таким образом, основным вопросом построения индексов,
общих и сводных состоит в том, чтобы обеспечить эту сопоставимость

Самый лёгкий способ сопоставления – сложные явления разбиваются на
простые элементы которые в известной мере являются однородными.

Общий индекс обозначается – I. Различают агрегатные и средневзвешенные индексы.

Основной формой сводного индекса является агрегатный индекс. Для
того, чтобы его построить необходимо свести различные элементы сложного явления
к такому виду, который делает их соизмеримыми.

– агрегатный индекс физического объёма
продукции(Ласпейреса).

– агрегатный индекс физического объёма
продукции(Пааше).

– агрегатный индекс цены (Ласпейреса).

– агрегатный индекс цены (Пааше).

– агрегатный индекс товарооборота.

– индекс издержек
производства.

Та часть индекса, которая не изменяется, называется весом.

Веса свободного индекса в агрегатной форме выбираются исходя из
следующих данных:

Если индексируемая величина – суть количественный
показатель, то вес выбирается на уровне базисного периода.

В том случае если индексируется величина – качественный признак вес
принимается на уровне текущего периода. Такой подход к выбору весов даёт нам
возможность записать следующее равенство индексов

Итак, в целом по совокупности, состоящей из элементов, непосредственно
несоизмеримых (различные виды продукции, товарные группы и т.д.), изменение
физического объема реализации и цен характеризуется с помощью агрегатных
индексов, формулы построения которых сведены в табл. 1.

Таблица 1

Агрегатные индексы

Формулы индексов	Название индексов
Индекс физического объема и других первичных признаков	Индекс цен и других вторичных признаков
По формуле Ласпейреса (по базисным весам)
По формуле Пааше (по отчетным весам)
Индекс Фишера

Пример:

Товары	Ед. измер	Базисный период	Текущий период	Индивидуаль-ный индекс
		P0 , (руб)	Q0 (ед.)	P1	Q1
Капуста	Кг.	17	350000	15	420000	0,882	1,2
Молоко	Литры	28	25400	35	23600	1,25	0,929
Яйца	Десятки	120	125	120	140	1	1,29

Индекс товарооборота:

Это значит товарооборот текущего периода по отношению к базисному вырос
на 7% этот показатель отражает изменение товарооборота под влиянием р и q.

Индекс физического объёма продукции (Ласпейраса):

Это значит товарооборот в текущем периоде возрос на 17% в связи с
изменением объёма реализации.

Индекс цены (Пааше):

Индекс цены показал нам, что стоимость продукции в текущем периоде по
сравнению с базисным сократился на 9% под влиянием изменения цен.

7.3.
Средние индексы

Агрегатная форма индекса – его основная форма, но не единственная в
ряде случаев для удобства расчётов в том случае если мы располагаем значениями
индивидуальных индексов на практике удобно использовать средние индексы.

Средний индекс – индекс, вычисленный как
средняя величина из индивидуальных индексов.

Средний гармонический индекс цены:

Средний арифметический индекс физического объема:

Цепные индексы – ряд индексов одного и того же
явления, вычисленных с меняющейся от индекса к индексу базой сравнения.

7.4. Индексы структурных сдвигов

При изучении динамики показателей приходится
определять изменение средней величины индексируемого показателя, которое
обусловлено взаимодействием двух факторов – изменением значения индексируемого
показателя у отдельных групп единиц и изменением структуры явления, т.е.
изменением доли отдельных групп единиц совокупности в общей их численности. Для
этого вычисляются три индекса: переменного состава, постоянного состава и
структурных сдвигов.

Индекс переменного состава – индекс,
выражающий соотношение средних уровней изучаемого явления, относящихся к разным
периодам времени. Он отражает изменение не только индексируемой величины, но и
структуры совокупности (весов).

– индекс п.с. себестоимости продукции.

Индекс постоянного (фиксированного) состава –
индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо
периода, и показывающий изменение только индексируемой величины. Это агрегатный
индекс.

– индекс ф.с. себестоимости продукции.

Индекс структурных сдвигов – индекс,
характеризующий влияние изменения структуры изучаемого явления на динамику
среднего уровня этого явления.

– индекс с.с. себестоимости продукции.

Существует взаимосвязь между этими индексами: .

Пример: по имеющимся данным о себестоимости
единицы продукции на трех предприятиях в текущем и базисном периодах получили
следующие индексы структурных сдвигов

средняя себестоимость по трем
предприятиям снизилась в текущем периоде по сравнению с базисным на 3,25%.

себестоимость в текущем периоде по
сравнению с базисным возросла в среднем на 2,1%.

изменение доли предприятий в общем объеме
произведенной продукции привело к снижению себестоимости на 5,24%.

Рекомендуемая литература

1.
Елисеева И.И., Юзбашев М.М. Общая теория
статистики: Учебник. – М.: ИНФРА-М, 1998.

2.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая
теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.: ИНФРА-М, 2001. – 416
с. — (Серия «Высшее образование»).

3.
Практикум по теории статистики: Учеб. Пособие / Под
ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.- 416 с.: ил.

4.
Теория статистики: Учебник / Под ред. проф. Р.А.
Шмойловой. – 3-е изд., перераб. – М.: Финансы и статистика, 2001.- 506 с.: ил.

5.
Теория статистики: Учебно-практическое пособие для
системы дистанционного образования /Под ред. В.Г. Минашкина. – М.: МЭСИ, 1998.

Виктория
Николаевна Шайкина

общая теория статистики

Учебное
пособие

Под ред.
В.В. Лихолетова

Технический
редактор А.В. Миних

Издательство Южно-Уральского государственного университета

Подписано
в печать

Формат
60х84 1/16. Печать офсетная. Усл. печ. л. Уч.-изд. л.

Тираж 100 экз. Заказ . Цена р.

Отпечатано
в типографии Издательства ЮУрГУ. 454080,
г. Челябинск,

пр. им. В.И.Ленина, 76

Источник

Метод частных средних

Простая линейная регрессия

Что такое среднее арифметическое число

Как найти среднее арифметическое число

Особенности работы с отрицательными числами

Натуральные и десятичные дроби

Средняя величина — это что такое?

Зачем она используется?

Сферы применения

Средняя величина в статистике

Как правильно рассчитать

Условия правильного вычисления

Классы СВ

Виды степенных СВ

Виды структурных величин

Виды средних величин

Показатели вариации

Средняя арифметическая простая (рассчитывается по несгруппированным данным):

Тема 5. ПОКАЗАТЕЛИ ВАРИАЦИИ

Хi–Х

Текущий период

Средняя
арифметическая простая (рассчитывается по несгруппированным данным):

Тема 5. ПОКАЗАТЕЛИ
ВАРИАЦИИ

Х_i–Х