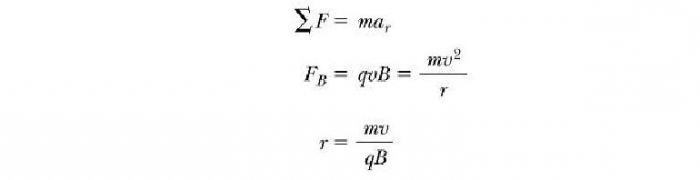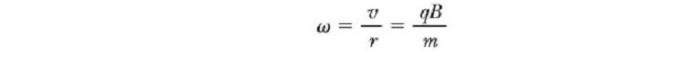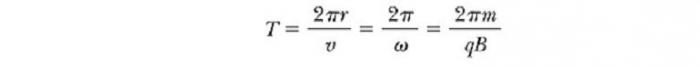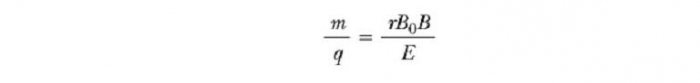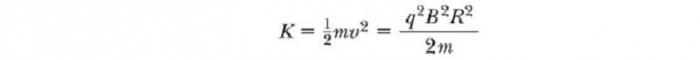Как найти частоту движения частицы

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

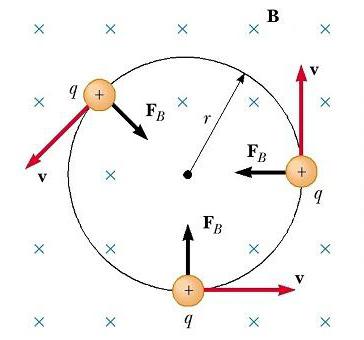
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

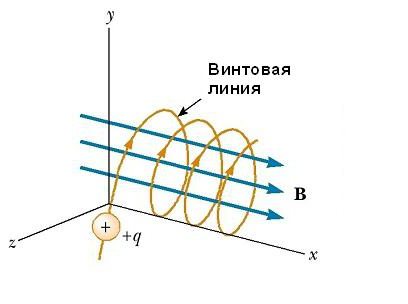
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

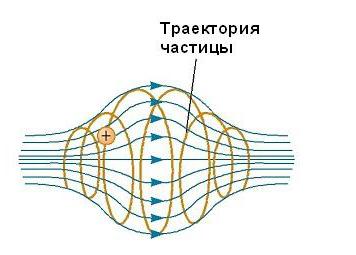
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

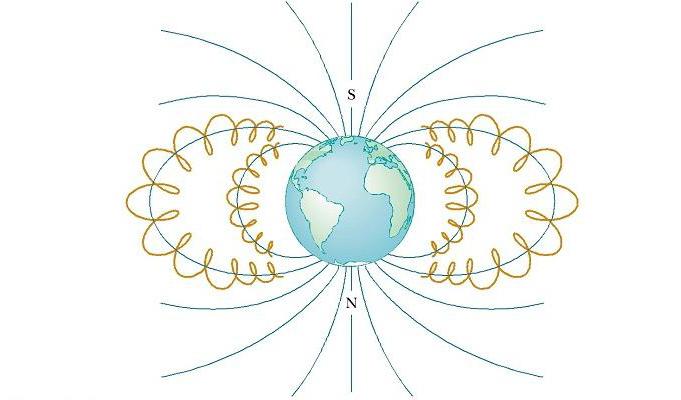
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

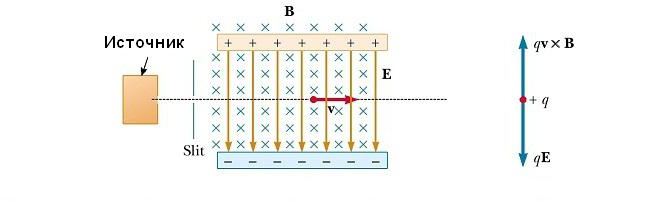
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

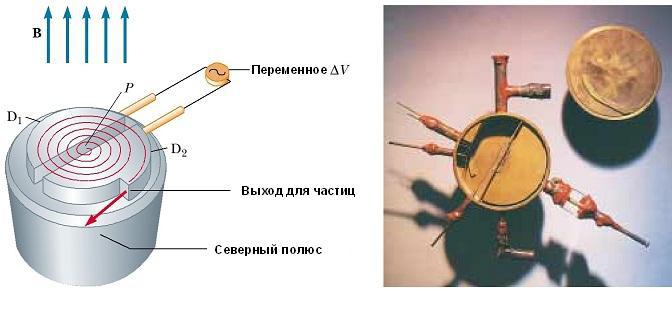
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость

лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:

(6.14.1)

где
m,v,q
– масса, скорость и заряд частицы.

Сила
Лоренца в этом случае играет роль
центростремительной силы .

Период
обращения частицы в однородном

магнитном
поле равен:

Это
выражение показывает, что для заряженных
частиц заданной массы m
период обращения не зависит от скорости
υ
и радиуса траектории r.

Угловая
скорость движения заряженной частицы
по круговой траектории:

(6.14.2)

Подставим
в полученное выражение (6.14.2) выражение
для радиуса траектории частицы (6.14.1),
получим:

называется
циклотронной
частотой.
Циклотронная частота не зависит от
скорости (следовательно, и от кинетической
энергии) частицы. Это обстоятельство
используется в циклотронах
– ускорителях тяжелых частиц (протонов,
ионов).

6.15 Выполняется ли принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях?

Движение
частицы, находящейся в электромагнитном
поле, описывается следующим уравнением.

Второй
закон Ньютона: 

Заряженная
частица, обладающая зарядом q,
движется в электромагнитном поле
согласно этому уравнению. Видим, что
сила, действующая на частицу со стороны
электромагнитного поля, определяется
двумя векторными полями: поле
 называется
напряжённостью электрического поля,
поле
 
— индукция магнитного поля. Они разделены,
потому что влияние их на частицу различны.
Поле
 не
содержит никаких характеристик частицы
кроме заряда. Если v
= 0, то второе слагаемое обращается в
ноль. Это означает, что магнитное поле
действует только на движущиеся частицы.
Неподвижные заряды не чувствуют
магнитного поля.

Следовательно,
принцип независимости движения для
заряженных частиц, движущихся одновременно
в электрическом и магнитном полях,
выполняется.

6.16
Электрон, обладающий скоростью v, попадает
в однородное магнитное поле, индукция
которого перпендикулярна скорости v.
Окружность, какого радиуса описывает
электрон?

Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость

лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:

где
m,
q
– масса и заряд частицы.

Заряд
электрона q
= e,
масса m
= m_e.

Радиус
описываемой электроном окружности:

6.17
Заряженная частица, пролетая некоторую
область пространства, не отклоняется
от первоначального направления движения.
Можно ли на основании этого факта
утверждать, что магнитное поле в этой
области отсутствует?

Нельзя.
Заряженная частица не отклоняется от
первоначального направления движения
в магнитном поле в следующих случаях:

1)
В каждой точке магнитного поля существует
такое направление, вдоль которого на
движущуюся заряженную частицу магнитная
сила не действует. Это направление можно
назвать магнитной осью.
Существенно,
что для каждой точки поля существует
свое, отличное от других точек поля,
направление магнитной оси. Это направление
выбирают за направление вектора магнитной
индукции
.

При
движении вдоль линий поля (угол между
скоростью

и вектором
магнитной индукции 

равен нулю) на частицу не действует сила
— она движется прямолинейно.

2)
На частицу, движущуюся в скрещенных
электрическом и магнитном полях,
действуют электрическая сила
и
магнитная
сила Лоренца.
При условии E = υB
эти силы точно уравновешивают друг
друга. Если это условие выполняется,
частица будет двигаться равномерно и
прямолинейно.

6.18
Пучок протонов, попадая в некоторую
область пространства, отклоняется на
некоторый угол. Можно ли на основании
этого факта определить, каким полем
вызвано отклонение, электрическим или
магнитным?

Не
имея данных ни о направлении поля
действия поля, ни об изменении скорости
частиц (или их кинетической энергии)
при прохождении данной области установить
природу поля нельзя.

6.19
Протон и электрон, имеющие одинаковую
скорость, попадают в однородное магнитное
поле, индукция В которого перпендикулярна
скорости частиц. Как будут различаться
их траектории?

Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость

лежит в плоскости, перпендикулярной
вектору магнитной индукции

то частица будет двигаться по окружности
радиуса:

(6.19.1)

где
q,
m
– заряд и масса частицы.

Заряды
протона и электрона равны по величине,
но противоположны по знаку: |q_p|
= |q_e|
= |e|

Исходя
из формулы 6.19.1 радиус траектории частицы
пропорционален ее массе и при равенстве
скоростей, радиус траектории протона
будет больше радиуса траектории электрона
примерно в 1836 раз (соотношение масс
протона и электрона m_p/m_e
= 1836,15267).

Так
как эти частицы имеют противоположные
по знаку заряды, то и направление силы
Лоренца, действующий на них в магнитном
поле будет противоположно. Протон и
электрон будут двигаться по окружностям
в противоположных направлениях.

6.20
Протон и электрон, ускоренные одинаковой
разностью потенциалов, влетают в
однородное магнитное поле. Во сколько
раз радиус кривизны траектории протона
будет больше радиуса кривизны траектории
электрона?

Частица,
пройдя ускоряющую разность потенциалов
U,
приобретает кинетическую энергию,
равную:

(6.20.1)

где
q,
m
– заряд и масса частицы;

v
– скорость, которую приобретает частица.

Если
заряженная частица движется в однородном
магнитном поле под действием силы
Лоренца, а ее скорость

лежит в плоскости, перпендикулярной
вектору магнитной индукции
то
частица будет двигаться по окружности
радиуса:

(6.20.2)

Из
уравнения (6.20.1) найдем скорость частицы:

Полученное
выражение для скорости частицы
v
подставим в уравнение (6.20.2):

(6.20.3)

Заряды
протона и электрона равны по величине
и противоположны по знаку: |q_p|
= |q_e|
= |e|

С
учетом равенства абсолютной величины
зарядов и на основании формулы (5.20.3)
запишем соотношение радиусов кривизны
траекторий частиц:

В
справочной литературе приведено
соотношение масс протона и электрона
− m_p/m_e
= 1836,15267.

Окончательно
получаем:

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у² + ν_z²).

Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Заряженная частица стартует с одного конца винтовой линии, накрученной вдоль силовых линий, и движется вдоль нее, пока не достигнет другого конца, где она поворачивает свой ​​путь обратно. Эта конфигурация известна как «магнитная бутылка», поскольку заряженные частицы могут быть захвачены в нее. Она была использована, чтобы ограничить плазму, газ, состоящий из ионов и электронов. Такая схема плазменного заключения может выполнять ключевую роль в контроле ядерного синтеза, процессе, который представит нам почти бесконечный источник энергии. К сожалению, «магнитная бутылка» имеет свои проблемы. Если в ловушке большое число частиц, столкновения между ними вызывают утечку их из системы.

Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Для положительного q магнитная сила F_B=qv х В направлена вверх, а электрическая сила qE – вниз. Когда величины двух полей выбраны так, что qE = qvB, то частица движется по прямой горизонтальной линии через область поля. Из выражения qE = qvB мы находим, что только частицы, имеющие скорость v=E/B, проходят без отклонения через взаимно перпендикулярные электрическое и магнитное поля. Сила F_B, действующая на частицы, движущиеся со скоростью большей, чем v=E/B, оказывается больше электрической, и они отклоняются вверх. Те же из них, которые движутся с меньшей скоростью, отклоняются вниз.

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

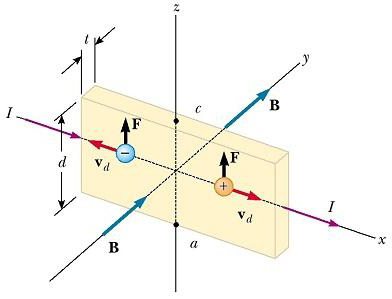
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Однородное поле B приложено в направлении у. Если носителями заряда являются электроны, движущиеся вдоль оси х со скоростью дрейфа v_d, то они испытывают направленную вверх (с учетом отрицательного q) магнитную силу F_B = qv_d х B, отклоняются вверх и накапливаются на верхнем краю плоского проводника, в результате чего появляется избыток положительного заряда на нижнем краю. Это накопление заряда на краях увеличивается до тех пор, пока электрическая сила, появившаяся в результате разделения зарядов, не уравновешивает магнитную силу, действующую на носители. Когда это равновесие будет достигнуто, электроны больше не отклоняются вверх. Чувствительный вольтметр или потенциометр, подключенный к верхней и нижней граням проводника, может измерить разность потенциалов, известную как ЭДС Холла.

Время на прочтение
7 мин

Количество просмотров 9.2K

1. Шар на пружине, ньютоновская версия
2. Квантовый шар на пружине
3. Волны, классический вид
4. Волны, классическое уравнение движения
5. Квантовые волны
6. Поля
7. Частицы – это кванты
8. Как частицы взаимодействуют с полями

Вернёмся к уравнению колебаний шара на пружине

В одной из первых статей цикла мы сначала вывели формулу для колебательного движения шара

А затем нашли уравнение движения, для которого эта формула была решением

Здесь
• d²z/dt² обозначает изменение по времени изменения по времени z(t).
• K – сила пружины, М – масса шара, z₀ — равновесное положение.
• ν = √ K/M / 2π

Ключевым шагом для получения последнего уравнения частоты, выраженной через К и М был подсчёт d²z/dt² для колебательного движения шара z(t) = z₀ + A cos [ 2 π ν t ]. Мы нашли, что

Уравнение движения волн

Теперь мы хотим сделать то же самое для волн. Мы нашли формулу для формы и движения волны, колеблющейся как в пространстве, так и во времени.

Среди решений какого уравнения движения есть такая формула? Можно представить себе ответ. Очевидно, в него входят:

1. d²Z/dt², изменение по времени изменения по времени Z(x,t).
2. d²Z/dx², изменение в пространстве изменения в пространстве Z(x,t).

Естественным образом мы можем догадаться, что уравнение должно выглядеть как-то так:

Где C_t, C_x и C₀ – константы. Отмечу, что если Где C_t = 1, C_x = 0, а C₀ = -K/M, вы вернёмся к уравнению колебания шара на пружине. Какие же это константы в нашем случае?

Мы всегда можем положить C_t = 1. Если бы вы захотели, допустим, положить C_t = 5, я бы просто попросил вас разделить всё уравнение на 5, что и дало бы вам эквивалент варианта, в котором C_t = 1, просто с другими значениями остальных констант.

После этого оказывается, что значения C_x и C₀ оказываются разными в различных физических системах. Мы изучим два разных класса волн, отличающихся разными константами.

У обеих классов C_x будет отрицательным,

(здесь c_w обозначает скорость перемещения высокочастотных волн).

Различаться эти классы будут тем, что у первого класса, Класс 1, C₀ будет отрицательным, и будет равняться –(2 π μ)2, а у второго, Класс 0, C₀ будет равно нулю.

Исследуем теперь свойства волн двух этих классов уравнений. Но до этого нужно провести ещё одно вычисление, которое мы уже делали ранее.

Быстрый подсчёт

Для нашей бесконечной волны

Нам нужно будет знать d²Z/dt² и d²Z/dx². В предыдущей статье мы уже показали, что для шара на пружине, движущегося согласно z(t) = z₀ + A cos [ 2 π ν t ], получается, что

. Изменение по времени даёт нам множитель 2 π ν, а изменение по времени изменения по времени даёт нам два множителя. Кроме того, тут есть общий знак минуса. Поэтому вас не удивит, что:

•

•

Каждое изменение по времени даёт нам множитель ν = 1/T (чем больше период, тем медленнее идёт изменение по времени), а каждое изменение в пространстве даёт нам множитель 1/λ (чем длиннее волна, тем медленнее изменение в пространстве).

Доказательство

Для бесконечной волны у нас есть основное уравнение

И мы хотим показать, что

Несколько фактов:

• Z – Z₀ = A cos (2π [ν t – x/λ]) (просто в основном уравнении перенесли Z₀ в левую часть)
• Поскольку Z₀ — константа, не зависящая от времени и пространства, dZ₀/dt = 0 and dZ₀/dx = 0.
• d(cos t)/dt = – sin t, и d(sin t)/dt = + cos t
• d(F[a t +b x])/dt = a d(F[a t +b x])/d(a t+ b x), где a и b – константы, а F – любая функция от (a t + b x).
• d[A f(t)]/dt = A d[f(t)]/dt, где f(t) – любая функция от t, а A — константа

Всё вместе это означает, что:

и

Поскольку основная формула для волны не изменится при замене (ν t) на (-x/λ), вычисление d²Z/dx² не отличается от вычисления d²Z/dt², просто вместо d/dt, дающего множитель (2π ν), у нас будет d/dx, дающий множитель (- 2π/λ). Но, поскольку в ответе есть два таких множителя, мы просто заменим (2π ν) ² на (- 2π/λ) ² = (+2π/λ) ²; минус значения не имеет (общий минус в сложении остаётся). Как нам и требовалось доказать,

Мелкий шрифт: все указанные выше производные на самом деле являются частными производными.

Класс 0: волны любой частоты и равных скоростей

В этом классе волн уравнение движения будет таким:

Подключив формулу Z(x,t) для бесконечной волны и используя только что сделанные нами подсчёты, мы находим, что:

Поделим уравнение на

, мы получим

Поскольку частоты, скорости и длины волн положительные, можно извлечь корень и получить

ν = c_w/λ, или, если хотите, λ = c_w/ν = c_w T

Из этой формулы мы узнаём, что:

• Изначально у нашей волны, так, как мы её записали, могла быть любая частота и любая длина волны. Но уравнение движения заставляет их зависеть друг от друга. Для волн класса 0 можно выбрать любую частоту, но после этого длина волны определяется через λ = c_w/ν.
• Все волны класса 0, вне зависимости от частоты, перемещаются со скоростью c_w. Это следует из формулы λ = c_w T и рис. 3 предыдущей статьи. Понаблюдайте, как волна проходит один цикл колебаний за время одного периода Т. Что происходит? Волна выглядит точно так же после Т, но каждый гребень сместился туда, где был его сосед – на расстояние λ. Это значит, что гребень передвигается на расстояние λ за время Т – одна длина волны за один период колебаний – и значит, что гребни движутся со скоростью λ / T = c_w. Это верно для всех частот и их периодов, и всех длин волн!
• Как и в случае с шаром на пружине, амплитуда А этих волн может быть любой, сколь угодно большой или малой. И это так для всех частот.

Класс 1: волны с частотой больше минимальной, с разными скоростями

Для этого класса волн наше уравнение движение будет таким:

Подставив формулу Z(x,t) для бесконечной волны и использовав быстрое вычисление, указанное выше, мы найдём, что

Поделив уравнение на

, мы получим

Поскольку частоты, скорости и длины волн положительные, мы можем извлечь квадратный корень и получить

Напомню, что y^1/2 — это то же самое, что √y.

Эта формула сильно отличается от формулы для волн класса 0, как и последствия её применения.

Во-первых, уравнение движения говорит о наличии минимально допустимой частоты. Поскольку (cw/λ) ² всегда положительно,

Чтобы приблизиться к ν = μ, необходимо увеличивать λ. Для очень больших длин волн частота приближается к μ, но меньше её стать не может. Для волн класса 0 это было не так. У них было ν = cw / λ, так что для них, чем больше вы делаете λ, тем сильнее ν приближается к нулю. Для волн класса 1 возможно любое значение ν, большее μ.

Во-вторых, мы нашли доказательство того, что у всех волн класса 0 скорость одинакова, но он не работает для волн класса 1. Единственный вариант, в котором он может сработать, если взять ν очень сильно больше, чем μ; для этого нам нужно сделать λ очень маленьким (и, соответственно, 1/ λ очень большим). В этом случае

То есть, на очень больших частотах и малых длинах волн у волн класса 1 будет примерно такое же соотношение между частотой и длиной волны, как у волн класса 0, поэтому по тем же причинам, что и волны класса 0, такие волны будут перемещаться со скоростью, (примерно) равной cw.

Что верно для волн обоих классов, так это то, что амплитуда А может быть любой, сколь угодно малой или большой, и не зависит от частоты.

Рис. 1. Для волн класса 0 и 1 уравнение движение даёт взаимосвязь между частотой, или периодом, и длиной волны, или 1/длину волны. На каждом из графиков показана взаимосвязь этих величин в зависимости от уравнения движения. Три графика показывают одно и то же, но построены они на разных переменных. Голубые линии относятся к волнам класса 0. Красные обозначают волны класса 1, скорость которых получается такой же на очень высоких частотах и малых длинах волн, когда они совпадают с голубыми линиями. Но на минимальной частоте μ (и с максимальным периодом 1/μ), обозначенных зелёным, две кривые расходятся при увеличении длин волн.

Мелкий шрифт: возможно, вы заметили, что я немножечко схитрил. Я не подсчитывал скорость волн класса 1. Дело в том, что здесь притаился очень хитрый подвох. У волн класса 0 я подсчитывал их скорость, следя за перемещениями гребней. Это работает потому, что в классе 0 волны всех частот перемещаются на одной скорости. Но у класса 1, или у любого другого, где волны разной частоты перемещаются с разной скоростью, скорость реальной волны не задаётся скоростью перемещения её гребней! Оказывается, что гребни движутся быстрее, чем cw, но скорость волны получается меньше, чем cw. Чтобы это понять, необходимо использовать весьма неочевидную логику и разницу между «групповой» и «фазовой» скоростью. Я пока обойду этот подвох; просто хотел обратить ваше внимание на его существование, чтобы вы не получили неправильное представление.

Финальные комментарии по поводу классических волн

Можно найти много знакомых примеров волн класса 0, включая звук в воздухе, воде или металле (где cw – скорость звуковых волн в материале), свет, и другие электромагнитные волны (где cw = с в вакууме), и волны на верёвках или струнах, как на рис. 2 в предыдущей статье. Поэтому волнам класса 0 обучают в начальных курсах физики. Не могу привести примера волн класса 1 в обычной жизни, но вскоре мы увидим, что эти волны так же важны для Вселенной.

У нас есть удобная формула E = 2 π² ν² A² M для энергии шара массы М на пружине. Формулы для других осцилляторов зависят от их природы, но их форма примерно такая же. Но в случае волн мы не упоминали их энергию. В частности из-за того, что мы для упрощения математики изучали волны с бесконечным числом гребней. Интуитивно понятно, что какая-то энергия должна храниться в движении и форме каждого гребня и впадины, и с бесконечным количеством гребней и впадин количество энергии в волне будет бесконечным. Это можно обойти двумя путями. Точные формулы зависят от типа волны, но давайте рассмотрим волны класса 0 на верёвке.

• Количество энергии на одну длину волны (хранящееся в промежутке между точкой x и точкой x + λ), конечно, и равно 2 π² ν² A² M_λ, где M_λ — масса отрезка верёвки длиной λ.
• В реальности волны не бывают бесконечными. Как импульс из нескольких гребней и впадин, показанный на рис. 2 в прошлой статье, любая волна будет конечной, у неё будет конечное количество гребней и впадин. Если она протянется на длину L, то есть, у неё будет L/λ гребней, тогда переносимая ей энергия будет равнятся 2 π² ν² A² M_L, где M_L — масса отрезка верёвки длиной L. Это просто L/λ, умноженное на энергию на одну длину волны.

Для волн, распространяющихся не по верёвкам, детали уравнений будут отличаться, но энергия на одну длину волны простой колебательной системы всегда будет пропорциональной ν² A².

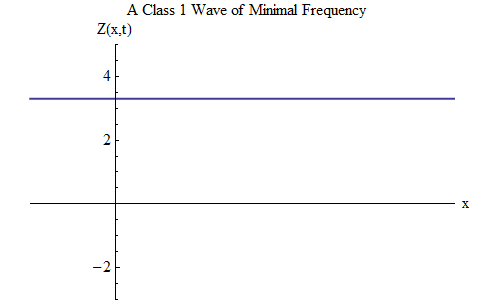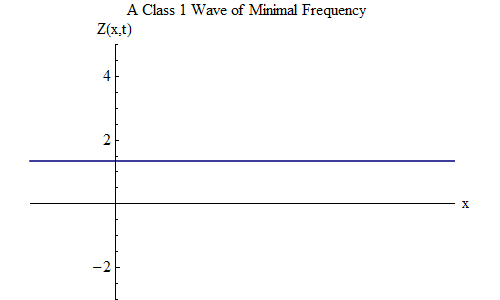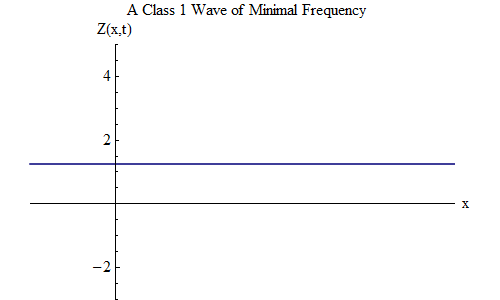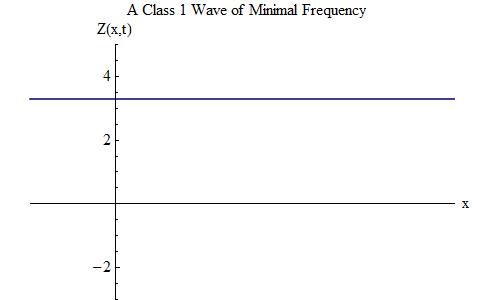
В классе 1 существует очень интересная волна, которой не бывает в классе 0. Это случай, когда ν = μ, минимальному значению, а λ = бесконечности. В этом случае волна принимает вид

Эта волна не зависит от x в любое время, то есть Z(x,t) будет константой по всему пространству, а Z колеблется во времени точно так, как шар на пружине с частотой μ. Такая стационарная волна, показанная на рис. 2, окажется очень важной в дальнейших рассуждениях.

Рис. 2

Квантовые волны

Для шара на пружине разница между классической и квантовой системой была в том, что в первом случае амплитуда могла принимать произвольные значения, как и энергия, а в квантовом случае амплитуда и энергия квантовались. Для любой похожей колебательной системы это работает таким же образом. Возможно, мы можем догадаться, что это выполняется и для волн…