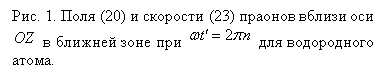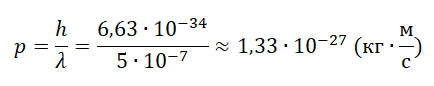Как найти частоту фотона при переходе - Исправление недочетов и поиск решений вместе с Examum.ru

Атом Бора.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев.

Темы кодификатора ЕГЭ: постулаты Бора.

Планетарная модель атома, успешно истолковав результаты опытов по рассеянию alpha -частиц, в свою очередь столкнулась с очень серьёзными трудностями.

Как мы знаем, любой заряд, движущийся с ускорением, излучает электромагнитные волны. Это — неоспоримый факт классической электродинамики Максвелла, подтверждаемый многочисленными наблюдениями.

Нам также хорошо известно, что электромагнитные волны несут энергию. Стало быть, ускоренно движущийся заряд, излучая, теряет энергию, которая этим излучением уносится.

А теперь давайте возьмём произвольный электрон в планетарной модели. Он двигается вокруг ядра по замкнутой орбите, так что направление его скорости постоянно меняется. Следовательно, электрон всё время имеет некоторое ускорение (например, при равномерном движении по окружности это будет центростремительное ускорение), и поэтому должен непрерывно излучать электромагнитные волны. Расходуя свою энергию на излучение, электрон будет постепенно приближаться к ядру; в конце концов, исчерпав запас своей энергии полностью, электрон упадёт на ядро.

Если исходить из того, что механика Ньютона и электродинамика Максвелла работают внутри атома, и провести соответствующие вычисления, то получается весьма озадачивающий результат: расход энергии электрона на излучение (с последующим падением электрона на ядро) потребует совсем малого времени — порядка $10^{-8}$ секунды. За это время атом должен полностью «коллапсировать» и прекратить своё существование.

Таким образом, классическая физика предрекает неустойчивость атомов, устроенных согласно планетарной модели. Этот вывод находится в глубоком противоречии с опытом: ведь на самом деле ничего такого не наблюдается. Предметы нашего мира вполне устойчивы и не коллапсируют на глазах! Атом может сколь угодно долго пребывать в невозбуждённом состоянии, не излучая при этом электромагнитные волны.

Постулаты Бора.

Оставалось признать, что внутри атомов перестают действовать известные законы классической физики. Микромир подчиняется совсем другим законам.

Первый прорыв в познании законов микромира принадлежит великому датскому физику Нильсу Бору. Он предложил три постулата, резко расходящиеся с механикой и электродинамикой, но тем не менее позволяющих правильно описать простейший из атомов — атом водорода.

Классическая физика хорошо описывает непрерывные процессы — движение материальной точки, изменение состояния идеального газа, распространение электромагнитных волн… Энергия объекта, подчиняющегося механике или электродинамике, в принципе может принимать любые значения. Однако линейчатые спектры указывают на дискретность процессов, происходящих внутри атомов. Эта дискретность должна фигурировать в законах новой теории.

Первый постулат Бора. Всякий атом (и вообще, всякая атомная система) может находиться не во всех состояниях с любым, наперёд заданным значением энергии. Возможен лишь дискретный набор избранных состояний, называемых стационарными, в которых энергия атома принимает значения $E_{1}, E_{2},...E_{n},...$ Находясь в стационарном состоянии, атом не излучает электромагнитные волны.

Как видим, первый постулат Бора вопиющим образом противоречит классической физике: налагается запрет на любые значения энергии, кроме избранного прерывистого набора, и признаётся, что электроны, вроде бы движущиеся ускоренно, на самом деле не излучают.

Выглядит фантастически, не правда ли? Однако в том же 1913 году, когда Бор предложил свои постулаты, существование стационарных состояний было подтверждено экспериментально — в специально поставленном опыте немецких физиков Франка и Герца. Таким образом, стационарные состояния — это не выдумка, а объективная реальность.

Значения разрешённого набора $E_{1}, E_{2},...E_{n},...$ называются уровнями энергии атома. Что происходит при переходе с одного уровня энергии на другой?

Второй постулат Бора. Если атом переходит из стационарного состояния с большей энергией $E_{n}$ в стационарное состояние с меньшей энергией $E_{k}$ , то разность этих энергий может высвободиться в виде излучения. В таком случае излучается фотон с энергией

$hnu =E_{n}-E_{k}$ . (1)

Эта же формула работает и при поглощении света: в результате столкновения с фотоном атом переходит из состояния $E_{k}$ в состояние с большей энергией $E_{n}$ , а фотон при этом исчезает.

Для примера на рис. 1 показано излучение фотона при переходе атома с энергетического уровня $E_{3}$ на уровень $E_{1}$ . Переход заключается в том, что электрон «соскакивает» с одной орбиты на другую, расположенную ближе к ядру.

Рис. 1. Излучение фотона атомом

Формула (1) даёт качественное представление о том, почему атомные спектры испускания и поглощения являются линейчатыми.

В самом деле, атом может излучать волны лишь тех частот, которые соответствуют разностям значений энергии разрешённого дискретного набора $E_{1}, E_{2},...E_{n},...$ ; соответственно, набор этих частот также получается дискретным. Вот почему спектр излучения атомов состоит из отдельно расположенных резких ярких линий.

Вместе с тем, атом может поглотить не любой фотон, а только тот, энергия hnu которого в точности равна разности $E_{n}-E_{k}$ каких-то двух разрешённых значений энергии $E_{n}$ и $E_{k}$ . Переходя в состояние с более высокой энергией $E_{n}$ , атомы поглощают ровно те самые фотоны, которые способны излучить при обратном переходе в исходное состояние $E_{k}$ . Попросту говоря, атомы забирают из непрерывного спектра те линии, которые сами же и излучают; вот почему тёмные линии спектра поглощения холодного атомарного газа находятся как раз в тех местах, где расположены яркие линии спектра испускания этого же газа в нагретом состоянии.

Качественного объяснения характера атомных спектров, однако, недостаточно. Хотелось бы иметь теорию, позволяющую вычислить частоты наблюдаемых спектров. Бору удалось это сделать в самом простом случае — для атома водорода.

Атом водорода.

Атом водорода состоит из ядра с зарядом , которое называется протоном, и одного электрона с зарядом (через обозначена абсолютная величина заряда электрона). При построении своей теории атома водорода Бор сделал три дополнительных предположения.

1. Прежде всего, мы ограничиваемся рассмотрением только круговых орбит электрона. Таким образом, электрон движется вокруг протона по окружности радиуса с постоянной по модулю скоростью (рис. 2).

Рис. 2. Модель атома водорода

2. Величина mvr , равная произведению импульса электрона на радиус орбиты , называется моментом импульса электрона. В каких единицах измеряется момент импульса?

Смотрим:

[mvr] =кг*м/с*м=(кг*м/ $c^{2}$ )*м*с=Н*м*с=Дж*с.

Это в точности размерность постоянной Планка! Именно здесь Бор увидел появление дискретности, необходимой для квантового описания атома водорода.

Правило квантования (третий постулат Бора). Момент импульса электрона может принимать лишь дискретный набор значений, кратных «перечёркнутой» постоянной Планка:

$mvr=nh^{mkern -14mu-}, (n=1,2,3,...)$ , (2)

3. Выше мы говорили, что классическая физика перестаёт работать внутри атома. Так оно в действительности и есть, но вопреки этому мы предполагаем, что электрон притягивается к протону с силой, вычисляемой по закону Кулона, а движение электрона подчиняется второму закону Ньютона:

$dfrac{mv^{2}}{r}=dfrac{ke^{2}}{r^{2}}$ . (3)

Эти три предположения позволяют довольно просто получить формулы для уровней энергии атома водорода. Переписываем соотношение (3) в виде:

$mv^{2}=dfrac{ke^{2}}{r^{2}}$ . (4)

Из правила квантования (2) выражаем :

$v=dfrac{nh^{mkern -14mu-}}{mr}$ ,

и подставляем это в (4):

$dfrac{n^{2}(h^{mkern -14mu-})^{2}}{mr^{2}}=dfrac{ke^{2}}{r}$ .

Отсюда получаем формулу для допустимых радиусов орбит электрона:

$r_{n}=dfrac{(h^{mkern -14mu-})^{2}n^{2}}{kme^{2}}$ . (5)

Теперь перейдём к нахождению энергии электрона. Потенциальная энергия кулоновского взаимодействия электрона с ядром равна:

$W=dfrac{k(+e)(-e)}{r}=- dfrac{ke^{2}}{r}.$

(Она отрицательна, так как отсчитывается от бесконечно удалённой точки, в которой достигает максимального значения.)

Полная энергия электрона равна сумме его кинетической и потенциальной энергий:

$E=dfrac{mv^{2}}{2}-dfrac{ke^{2}}{r}$ .

Вместо $mv^{2}$ подставим правую часть выражения (4):

$E=dfrac{ke^{2}}{2r}-dfrac{ke^{2}}{r}=-dfrac{ke^{2}}{2r}$ . (6)

Полная энергия, как видим, отрицательна. Если на радиус орбиты никаких ограничений не накладывается, как это имеет место в классической физике, то энергия может принимать любые по модулю значения. Но согласно (5) существует лишь дискретный набор возможных значений радиуса; подставляя их в (6), получаем соответствующий набор допустимых значений энергии атома водорода:

$E=-dfrac{ke^{2}}{2r_{n}}=-dfrac{k^{2}me^{4}}{2(h^{mkern -14mu-})^{2}n^{2}}, (n=1,2,3,...)$ . (7)

Основное состояние атома водорода — это состояние с наименьшей энергией $E_{1}$ . В основном состоянии атом может находиться неограниченно долго. Вычисление даёт:

$E_{1}=-2,18 cdot 10^{-18}$ Дж =-13,6 эВ:

Мы видим, что если атом находится в основном состоянии, то для выбивания электрона нужно сообщить атому энергию, равную как минимум 13,6 эВ. Эта величина носит название энергии ионизации атома водорода.

По формуле (5) легко вычислить радиус орбиты основного состояния:

$r_{1}=dfrac{(h^{mkern -14mu-})^{2}}{kme^{2}}=5cdot 10^{-9}$ см.

То есть, диаметр атома оказывается равным как раз $10^{-8}$ см — величине, известной из опыта. Таким образом, теория Бора впервые смогла объяснить размер атома!

Кроме того, в рамках теории Бора удаётся получить формулы для вычисления частот (или длин волн) спектра атома водорода. Так, согласно второму постулату Бора и формуле (7) имеем:

$nu =dfrac{E_{n}-E_{k}}{h}=dfrac{k^{2}me^{4}}{4pi (h^{mkern -14mu-})^{3}}(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})$ . (8)

На практике чаще имеют дело с длинами волн. Учитывая, что , формулу (8) можно переписать так:

$dfrac{1}{lambda} =dfrac{k^{2}me^{4}}{4pi (h^{mkern -14mu-})^{3}}(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})=R(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})$ . (9)

Константа $R=1,1 cdot 10^{-7}$ м $^{-1}$ называется постоянной Ридберга. Теория Бора даёт значение этой постоянной, очень хорошо согласующееся с экспериментом.

Длины волн спектра атома водорода образуют серии, характеризующиеся фиксированным значением в формуле (9). Все длины волн данной серии излучаются при переходах на уровень $E_{k}$ с вышележащих энергетических уровней $E_{n}, (n=k+1, k+2, k+3,...)$ .

Переходы в основное состояние:

$E_{2}rightarrow E_{1}, E_{3}rightarrow E_{1}, E_{4}rightarrow E_{1},...$

образуют серию Лаймана. Длины волн этой серии описываются формулой (9) при k=1 :

$dfrac{1}{lambda} =R(1-dfrac{1}{n^{2}})$ .

Линии серии Лаймана лежат в ультрафиолетовом диапазоне.

Переходы на второй уровень:

$E_{4}rightarrow E_{2}, E_{3}rightarrow E_{2}, E_{5}rightarrow E_{2},...$

образуют серию Бальмера. Длины волн этой серии подчиняются формуле (9) при k=2 :

$dfrac{1}{lambda} =R(dfrac{1}{4}-dfrac{1}{n^{2}})$ .

Первые четыре линии серии Бальмера лежат в видимом диапазоне (рис. 3), остальные — в ультрафиолетовом.

Рис. 3. Видимый спектр атома водорода (серия Бальмера)

Переходы на третий уровень:

$E_{4}rightarrow E_{3}, E_{5}rightarrow E_{3}, E_{6}rightarrow E_{3},...$

образуют серию Пашена. Длины волн этой серии описываются формулой (9) при k=3 :

$dfrac{1}{lambda} =R(dfrac{1}{9}-dfrac{1}{n^{2}})$ .

Все линии серии Пашена лежат в инфракрасном диапазоне.

Имеются ещё три «именованных» серии: это серия Брэккета (переходы на уровень k=4 ), серия Пфунда (переходы на уровень k=5 ) и серия Хэмпфри (переходы на уровень k=6 ). Все линии этих серий лежат в далёкой инфракрасной области.

Достоинства и недостатки теории Бора.

О достоинствах модели атома водорода, предложенной Бором, мы так или иначе уже сказали. Резюмируем их.

— Теория Бора продемонстрировала, что для описания атомных объектов принципиально недостаточно представлений классической физики. В микромире работают другие, совершенно новые законы.
Для микромира характерно квантование — дискретность изменения величин, описывающих состояние объекта. В качестве меры квантования, как показала теория Бора, может выступать постоянная Планка $h^{mkern -14mu-}$ , которая является универсальной константой и играет фундаментальную роль во всей физике микромира (а не только в явлениях излучения и поглощения света).

— Теория Бора впервые и совершенно точно указала на факт наличия стационарных энергетических состояний атома, образующих дискретный набор. Этот факт оказался общим свойством объектов микромира.

— В рамках модели Бора удалось получить формулы для вычисления частот спектра атома водорода и объяснить размер атома. Классическая физика была не в состоянии решить эти проблемы.

Однако теория Бора, разумеется, не могла претендовать на роль общей теории, описывающей микромир. Модель Бора обладала рядом существенных недостатков.

— Теория Бора непоследовательна. С одной стороны, она отвергает описание атома на основе классической физики, так как постулирует наличие стационарных состояний и правила квантования, непонятных с точки зрения механики и электродинамики. С другой стороны, классические законы — второй закон Ньютона и закон Кулона — используются для записи уравнения движения электрона по круговой орбите.

— Теория Бора не смогла дать адекватное описание самого простого после водорода атома гелия. Подавно не могло быть и речи о распространении теории Бора на более сложные атомы.

— Даже в самом атоме водорода теория Бора смогла описать не всё. Например, дав выражения для частот спектральных линий, модель Бора не объясняла различие в их интенсивностях. Кроме того, неясен оставался механизм образования молекулы водорода из двух атомов.

Несмотря на свои недостатки, теория Бора стала важнейшим этапом развития физики микромира. Полуклассическая-полуквантовая модель Бора послужила промежуточным звеном между классической физикой и последовательной квантовой механикой , построенной десятилетием позже — в 1920-х годах.

Разберем задачи ЕГЭ на темы: «Строение атома», «Модель Резерфорда-Бора», «Энергетические уровни», «Излучение фотона».

Задача 1.

На рисунке изображена схема низших энергетических уровней атома. В начальный момент времени атом находится в состоянии с энергией Е⁽²⁾. Согласно постулатам Бора, с какой энергией данный атом может излучать фотоны? (Ответ дать в 10⁻¹⁹ Дж.)

Решение:

Согласно постулатам Бора, атом, находящийся в стационарных состояниях, не излучает энергии. Излучение энергии возможно при переходе атома с уровня с большим значением энергии на уровень с меньшим значением энергии. Поглощение энергии, наоборот, возможно при переходе атома с меньшим уровнем энергии на больший.

С учетом представленной диаграммы, излучение атома возможно при переходе с уровня Е⁽²⁾ на уровень Е⁽¹⁾, так как Е⁽²⁾> Е⁽¹⁾. Поэтому, энергия излучаемых фотонов (hv) может быть определена, как разность энергий

$hnu=E^{(2)}-E^{(1)}.$

Подставив численные значения, рассчитаем энергию излучаемых фотонов.

$hnu=-5cdot 10^{-19}-(-8cdot 10^{-19})=-5cdot 10^{-19}+8cdot 10^{-19}=3cdot 10^{-19}$ (Дж).

Ответ: 3.

Задача 2.

Электрон в атоме водорода находится в основном (самом низком, с номером n = 1) энергетическом состоянии. Атом поглощает фотон с импульсом 6,8 · 10^–27 кг·м/с. Найдите номер энергетического уровня, на который в результате этого перейдёт электрон.

Дано:
n₁=1;
p = 6,8·10^–27 кг·м/с.

Найти:
n-?

Решение:

Уровни энергии в атоме водорода определяются формулой:

$E_{n}=dfrac{-13,6}{n^{2}}$ (эВ), где n=1, 2, 3… и т. д. (1)

Следовательно, атом на уровне n₁=1 обладает энергией, которую можно рассчитать по формуле (1).

$E_{1}=dfrac{-13,6}{1^{2}}=-13,6$ (эВ).

Найдем связь между импульсом фотона и его энергией:

p=mc;

$E=hnu =mc^{2};$

(2)

Таким образом, энергия фотона может быть определена по формуле (2).

$E=6,8cdot 10^{-27}cdot 3cdot 10^{8}=20,4cdot 10^{-19}$ (Дж).

С учетом, что 1 эВ $=1,6cdot 10^{-19}$ , получим $E=dfrac{20,4cdot 10^{-19}}{1,6cdot 10^{-19}}=12,75$ (эВ).

Атом, получив энергию от фотона, переходит в стационарное состояние с большим уровнем энергии.

$E_{n}=E_{1}+E;$

$E_{n}=-13,6+12,75=-0,85$ (эВ).

Из формулы (1) необходимо вывести номер энергетического уровня.

$n=sqrt{dfrac{-13,6}{E_{n}}};$

$n=sqrt{dfrac{-13,6}{-0,85}}=4.$

Ответ: 4.

Задача 3.

На рисунке изображена упрощенная диаграмма нижних энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какой из этих четырех переходов связан с поглощением света наибольшей энергии, а какой — с излучением света с наибольшей длиной волны?

Установите соответствие между процессами поглощения и испускания света и стрелками, указывающими энергетические переходы атома.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ПРОЦЕССЫ
А) поглощение света наибольшей энергии;
Б) излучение света с наибольшей длиной волны.

ЭНЕРГЕТИЧЕСКИЕ ПЕРЕХОДЫ
1) 1
2) 2
3) 3
4) 4

Ответ:

Решение:

По указанной диаграмме необходимо определить переходы, соответствующие поглощению и излучению света.

Переходы, указанные стрелками 1 и 2, соответствуют излучению энергии, так как атом переходит с большего уровня энергии на меньший.

Здесь надо учесть, что

$Delta E_{10} =E_{1}-E_{0}$ и $Delta E_{20}=E_{2}-E_{0}.$

Так как $Delta E_{20} textgreater Delta E_{10}$ , то, согласно формуле Планка $E=hnu =hdfrac{c}{lambda }$ , меньшая длина волны соответствует большему значению энергии излучения. Поэтому при переходе 2to 0 будет излучаться большее количество энергии. Вторая стрелка будет соответствовать излучению света с наименьшей длиной волны.

Стрелки 3 и 4 соответствуют поглощению энергии, так как в этих случаях атом переходит на уровни, соответствующие большему значению энергии. Рассуждения, аналогичные первому случаю, приводят к следующему выводу:

$Delta E_{30} =E_{3}-E_{0}$ и $Delta E_{40}=E_{4}-E_{0}.$

Так как $Delta E_{40} textgreater Delta E_{30}$ , то четвертая стрелка будет соответствовать поглощению света наибольшей энергии.

Ответ:

Задача 4.

Значения энергии электрона в атоме водорода задаются формулой: $E_{n}=dfrac{-13,6}{n^{2}}$ (эВ), где n=1, 2, 3… и т. д.

При переходах с верхних уровней энергии на нижние атом излучает фотон. Переходы с верхних уровней на уровень c n = 1 образуют серию Лаймана, на уровень c n = 2 – серию Бальмера и т. д. Найдите отношение γ максимальной длины волны фотона в серии Бальмера к максимальной длине волны фотона в серии Лаймана.

Решение:

Рис. 1. Серия Лаймана

Согласно формуле Планка $E=hnu =hdfrac{c}{lambda }$ , максимальная длина волны соответствует излучению света с наименьшим значением энергии. Поэтому для серии Лаймана это переход с уровня 2 на уровень 1 (см. рис. 1). Рассчитаем значение энергии, которая излучается в этом случае.

$E_{21}=E_{2}-E_{1};$

$E_{21}=dfrac{-13,6}{2^{2}}-left ( -dfrac{-13,6}{1^{2}} right )=dfrac{-13,6}{2^{2}}+dfrac{13,6}{1^{2}}=10,2$ (эВ).

$E_{21}=10,2$ (эВ).

Длина волны, соответствующая этому переходу, может быть определена из формулы:

$E_{21}=hnu _{21}=hdfrac{c}{lambda _{21}};$

$lambda _{21}=hdfrac{c}{E_{21}}.$ (1)

Аналогично для серии Бальмера, излучение с наибольшей длиной волны (наименьшей энергии излучения), соответствует переходу с уровня 3 на уровень 2 (см. рис. 2).

Рис. 2. Серия Бальмера

$E_{32}=E_{3}-E_{2};$

$E_{32}=dfrac{-13,6}{3^{2}}-left ( -dfrac{-13,6}{2^{2}} right )=dfrac{-13,6}{3^{2}}+dfrac{13,6}{2^{2}}approx 1,89$ (эВ).

$E_{32}approx 1,89$ (эВ).

Длина волны, соответствующая этому переходу, может быть определена из формулы:

$E_{32}=hnu _{32}=hdfrac{c}{lambda _{32}};$

$lambda _{32}=hdfrac{c}{E_{32}}.$ (2)

Тогда, для нахождения соотношения для длин волн $gamma=dfrac{lambda _{32}}{lambda _{21}}.$

Разделим уравнение (2) на уравнение (1):

$gamma=dfrac{lambda _{32}}{lambda _{21}}=hdfrac{c}{E_{32}}div hdfrac{c}{E_{21}}=hdfrac{c}{E_{32}}cdot dfrac{E_{21}}{hcdot c}=dfrac{E_{21}}{E_{32}}.$

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{E_{21}}{E_{32}}.$

В расчетах значения энергий можно оставить в эВ, так как перевод в систему «СИ» ответа не изменит.

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{10,2}{1,89}approx 5,4.$

С учетом системы «СИ»:

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{10,2cdot 1,6cdot 10^{-19}}{1,89cdot 1,6cdot 10^{-19}}approx 5,4.$

(1 эВ $=1,6cdot 10^{-19}$ Дж).

Ответ: 5,4.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Атом Бора.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

In English

Journal of Fundamental and
Applied Sciences, Vol. 9, No. 1, pp. 411-467 (2017). http://dx.doi.org/10.4314/jfas.v9i1.25

Субстанциональная модель фотона

Федосин Сергей Григорьевич

ул.
Свиязева 22-79, город Пермь, 614088, Пермский край, Россия

e-mail intelli@list.ru

Показывается, что угловая частота фотона есть не что иное, как
усреднённая угловая частота вращения центра электронного облака за время
излучения и квантового перехода между двумя уровнями энергии в атоме. В
предположении, что фотон состоит из заряженных частиц вакуумного поля (праонов),
строится субстанциональная модель фотона. Праоны движутся внутри фотона таким
же образом, как они должны двигаться в электромагнитном поле излучающего
электрона, при этом у фотона возникает внутренняя периодическая волновая
структура. Свойства праонов, включая их массу, заряд и скорость движения,
выводятся в рамках теории бесконечной вложенности материи. При этом праоны
входят в состав нуклонов и лептонов так же, как нуклоны являются основой
нейтронных звёзд и вещества обычных звёзд и планет. С помощью преобразований
Лоренца, связывающих лабораторную систему отсчёта и систему отсчёта,
сопутствующую праонам внутри фотона, делается преобразование компонент
электромагнитного поля. Это позволяет вычислить продольное магнитное поле и
дипольный магнитный момент фотона, а также понять соотношение между поперечными
компонентами электрического и магнитного полей, связанных коэффициентом в виде
скорости света. Находится суммарная масса покоя частиц, составляющих фотон, при
этом она обратно пропорциональна зарядовому числу ядра водородоподобного атома,
излучающего фотон. В представленной картине фотон, будучи составленным из
праонов, движется со скоростью меньшей скорости света и теряет право называться
элементарной частицей ввиду своей сложной структуры.

Ключевые
слова: волны материи; квантовая гравитация;
электромагнитное взаимодействие; магнитные моменты; свойства фотона.

The substantial model of the photon

Sergey G. Fedosin

Sviazeva
Str. 22-79, Perm, 614088, Perm Krai, Russian Federation

e-mail intelli@list.ru

It is shown that the
angular frequency of the photon is nothing else than the averaged angular
frequency of revolution of the electron cloud’s center during emission and
quantum transition between two energy levels in an atom. On assumption that the
photon consists of charged particles of the vacuum field (of praons), the
substantial model of a photon is constructed. Praons move inside the photon in
the same way as they must move in the electromagnetic field of the emitting
electron, while internal periodic wave structure is formed inside the photon.
The properties of praons, including their mass, charge and speed, are derived
in the framework of the theory of infinite nesting of matter. At the same time,
praons are part of nucleons and leptons just as nucleons are the basis of
neutron stars and the matter of ordinary stars and planets. With the help of
the Lorentz transformations, which correlate the laboratory reference frame and
the reference frame, co-moving with the praons inside the photon,
transformation of the electromagnetic field components is performed. This
allows us to calculate the longitudinal magnetic field and magnetic dipole
moment of the photon, and to understand the relation between the transverse
components of the electric and magnetic fields, connected by a coefficient in
the form of the speed of light. The total rest mass of the particles making up
the photon is found, it turns out to be inversely proportional to the nuclear
charge number of the hydrogen-like atom, which emits the photon. In the
presented picture the photon composed of praons moves at a speed less than the
speed of light, and it loses the right to be called an elementary particle due
to its complex structure.

Keywords: matter waves; quantum gravity;
electromagnetic interaction; magnetic moments; properties of photon.

PACS: 03.65.-w, 11, 12.10.Dm, 42.25.-p

1. Введение

Как известно, чем элементарнее частица, тем меньше нам о ней известно. Не
исключением является и фотон, концепция которого появилась более ста лет назад
в трудах А. Эйнштейна. Загадочным кажется отсутствие массы покоя у этой
частицы, наличие одновременно волновых и корпускулярных свойств, высокая
стабильность и возможность перемещаться на космические расстояния с малыми
потерями энергии, неразрывная связь между фотонами и заряженными частицами в
процессах поглощения и излучения.

Одним из современных способов изучения структуры фотона являются
эксперименты по столкновению фотонов друг с другом, с протонами и электронами.
Эти эксперименты показывают, что при малых расстояниях фотон можно моделировать
в виде потоков кварков и глюонов [1]. Данные потоки должны участвовать во
взаимодействиях так, как это предписывается в квантовой электродинамике.

В осциллирующей модели [2] фотон рассматривается как периодически
изменяющий свой объём объект, скорость которого меньше скорости света. В этой
модели предполагается, что масса покоя фотона с наибольшей длиной волны может
быть связана с начальными условиями ранней Вселенной. Исходя из этого, делается
оценка массы внутренней части фотона: кг. В противоположность этому, в [3] считают, что фотон не
имеет собственной массы, однако под действием вакуумного поля возникает
эффективная масса.

В [4] диаметр фотона приравнивается к длине волны на том основании, что
этот размер есть предел для дифракции волны. Солитонная модель фотона строится
в [5], в которой используется уравнение для векторного потенциала, аналогичное
обобщённому уравнению Шрёдингера. В [6] указывается, что недостатком солитонной
модели является трудность с объяснением возникновения солитона, для чего обычно
требуется нелинейная среда. Диаметр фотона согласно [7] равняется , а за пределами фотона интенсивность его поля должна
уменьшаться обратно пропорционально расстоянию до оси фотона. Это позволяет
фотону осуществлять интерференцию в опыте Юнга. Описание фотона как вращающейся
частицы в рамках квантовой электродинамики представлено в [8].

Ввиду недостатка важнейшей информации о внутренних параметрах
электромагнитных квантов существующие модели всё ещё требуют доработки и
уточнения, так как не позволяют конкретизировать реальное устройство фотона,
связать его с источником излучения на атомном уровне и с экспериментальными
данными. Целью данной статьи является восполнить этот недостаток и представить
более подробную и достаточно обоснованную субстанциональную модель фотона. При
этом мы будем опираться на теорию бесконечной вложенности материи и субстанциальную
модель электрона [9].

Мы начнём с того, что рассмотрим общие условия излучения из
водородоподобного атома и оценим длительность излучения, что необходимо для
определения длины фотона в пространстве и последующего вычисления его плотности
энергии. В разделе 3 мы представляем основные компоненты электрического и
магнитного поля, создаваемые вращающимся вокруг ядра зарядом в ближней и в
волновой зоне. Поток энергии этих полей приводит к стандартной формуле для
излучения заряда. Нашей целью является использование отдельных компонент
электромагнитного поля вращающегося заряда для нахождения уравнений движения
мельчайших заряженных частиц вакуумного поля в разделе 4. Указанные частицы,
называемые праонами, мы рассматриваем как строительный материал не только для
фотонов, но и для любых других элементарных частиц, включая нуклоны и лептоны.
Праоны обладают массой и для описания их движения при релятивистских скоростях
мы используем фактор Лоренца. Это позволяет с помощью преобразований Лоренца
перейти в систему отсчёта, сопутствующую праонам, и понять их движение с точки
зрения неподвижного фотона.

В разделе 5, основываясь на движении праонов в периодически изменяющемся
в пространстве и времени электромагнитном поле излучающего электрона, мы строим
субстанциональную модель фотона. Раздел 6 посвящён структуре электромагнитного
поля и поля сильной гравитации внутри фотона, и их взаимодействию с праонами,
обеспечивающему стабильность фотона. В разделах 7, 8, 9 мы выводим
соответственно, фактор Лоренца для праонов и потоки энергии внутри фотона,
дипольный магнитный момент и массу покоя частиц, составляющих фотон.

2. Излучение фотона из водородоподобного атома

Согласно соотношению Бора, энергия фотона как электромагнитного кванта,
излучаемого при переходе электрона с одного уровня энергии на другой более низкий
уровень , равняется разности полных энергий электрона на этих
уровнях:

,
(1)

здесь − постоянная Дирака,

− угловая частота фотона.

Однако, как же описать более наглядно, что происходит в атоме при
излучении кванта? Для упрощения предположим, что один электрон находится в
центральном поле в водородоподобном атоме. Если вещество электрона полностью
симметрично вращается относительно ядра, то электрон не будет излучать. Это
является следствием того, что для каждого элемента заряда в веществе электрона
в осесимметричной конфигурации найдётся такой же элемент заряда с
противоположной стороны от оси, движущийся в противоположную сторону. На
больших расстояниях вклад ядра и указанных элементов заряда в полную
электрическую напряжённость поля и магнитную индукцию будет компенсирован, и
результирующий поток энергии станет близким к нулю.

Поэтому для излучения электрон должен двигаться так, чтобы центр его инерции
был в достаточной мере удалён от ядра. Пусть центр электронного облака
вращается на расстоянии от ядра и удерживается
в относительном равновесии силой, направленной к ядру. Если скорость центра
облака равна , то для равенства центральной и центростремительной сил
можно записать:

, , (2)

где − количество протонов
в ядре, − элементарный заряд, − электрическая
постоянная, − масса электрона, так
что представляет собой
электрическую силу между положительно заряженным ядром с зарядом и отрицательно
заряженным электроном.

В (2) мы поставили знак приблизительного равенства, так как при излучении
расстояние будет медленно
уменьшаться, а скорость увеличиваться. Кроме этого, мы здесь не учитываем
изменение собственной электромагнитной энергии облака за счёт изменения радиуса
и объёма самого облака при его приближении к ядру. Далее мы используем
стандартную формулу для мощности полного электромагнитного излучения от
элементарного заряда, вращающегося вокруг некоторого центра [10]. Если
излученную энергию за время с точностью до знака
считать равной изменению полной энергии электронного облака,
то можно записать:

,
(3)

здесь − скорость света, а
небольшой коэффициент отражает тот факт, что
излучение от электронного облака как объёмной фигуры должно отличаться от
излучения вращающегося электрона в виде точки.

Считая, что , где − угловая скорость
вращения центра электронного облака вокруг ядра, из соотношения для мощности и (3) найдём модуль
силы, тормозящей вращение облака:

.
(4)

Для момента импульса центра инерции облака и скорости его изменения под
действием момента силы можно записать:

, . (5)

Кроме этого имеем следующее:

,
,
(6)

то есть изменение энергии электронного облака при изменении момента
импульса центра облака пропорционально угловой частоте вращения.

Выражая из (2) скорость в виде 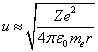и подставляя в (5), с
учётом (4) приходим к дифференциальному уравнению для зависимости расстояния от времени:

, , (7)

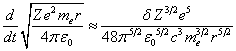
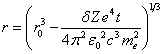
здесь − расстояние до центра
облака в начальный момент времени.

Выражение (7) приблизительно описывает небольшие изменения расстояния со временем для
вращательного движения электронного облака. При этом должно выполняться условие
, , где есть время падения
центра инерции облака на притягивающий центр.

Например, если предположить изменение расстояния от до , где обозначает радиус
Бора, то для времени перехода с уровня на уровень при и из (7) получается
значение порядка с, то есть типичное время излучения электромагнитного кванта
электроном в атомных переходах.

Если подставить расстояние (7) в (3) с учётом 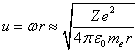и проинтегрировать по
времени, то найдётся полная энергия электронного облака:

.
(8)

Из (8) видно, что если электрон переходит с уровня энергии на уровень энергии , то энергия излученного электромагнитного кванта составит
величину, равную разности уровней энергий электрона в атоме: . Данное соотношение точно совпадает с условием Бора для
энергий. Этого и следовало ожидать, поскольку из (2) следует, что
электростатическая энергия электрона на уровне равна величине , а кинетическая энергия электрона . Полная энергия на уровне предполагается равной
сумме этих энергий: .

Из условия 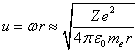и (3) следует, что
мощность излучения энергии сильно зависит от текущего расстояния :

.
(9)

Согласно (9) можно предположить, что основная энергия электромагнитного
кванта при переходе с уровня энергии на уровень энергии излучается электронным
облаком недалеко от уровня , где радиус вращения центра электронного
облака меньше. В таком случае мы находим
объяснение тому факту, что частота электромагнитных квантов в (1) близка, но
всегда меньше частоты вращения электронного облака вблизи уровня энергии . Если рассматривать в какой-то момент времени излученный
электромагнитный квант вдоль его длины в пространстве, то частота его колебаний
должна увеличиваться при переходе от передней части кванта до задней, а
плотность энергии кванта должна иметь максимум ближе к задней части кванта.

Постоянная была введена Планком в
1900 г. при установлении закона распределения энергии в спектре излучения
абсолютно чёрного тела. Данная постоянная оказалась универсальной величиной на
уровне элементарных частиц и атомов, имея размерность кванта действия. Её роль
в определении электромагнитной энергии квантов при том, что частота колебаний
волны внутри этих квантов по нашему мнению не может быть строго постоянна,
вполне аналогична роли постоянной Больцмана в определении средней тепловой
энергии множества частиц через температуру, при всегда имеющемся разбросе
энергий отдельных частиц.

Покажем, что угловая частота кванта является усреднённой
угловой частотой вращения центра
электронного облака при переходе между уровнями энергии и . Для с учётом (6) имеем:

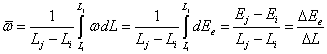
При энергия
электромагнитного кванта будет:

.
(10)

Из сравнения (10) и (1) видно, что . Однако, если по каким-то причинам , то равенство не будет иметь места.

Поскольку при излучении квантов меняется момент
импульса электрона, то изменение момента импульса должен уносить
электромагнитный квант. Фотонам, или электромагнитным квантам, приписывается
момент импульса, равный . Поэтому электрон при излучении теряет момент импульса
порядка , и такой же момент импульса получает фотон; электрон теряет
энергию порядка , где − средняя частота вращения центра
инерции электрона возле ядра за период излучения, а фотон приобретает эту
энергию. Электрон выступает в данном случае как переносчик своей кинетической
энергии и момента импульса в энергию и момент импульса электромагнитной волны, сосредоточенные в
излучаемом фотоне.

3. Излучение от вращающегося точечного заряда

Пусть точечная заряженная частица с зарядом вращается по
окружности радиуса с угловой скоростью и с орбитальной
скоростью . Расположим сферическую систему отсчёта в центре этой
окружности и будем искать компоненты напряжённости электромагнитного поля от
вращающегося заряда в некоторой удалённой точке с радиусом-вектором . Текущее положение заряда задаётся вектором , так что окружность вращения лежит в плоскости .

Для определения напряжённости электрического поля и
индукции магнитного поля в
первом приближении воспользуемся формулами, учитывающими любое движение заряда
в специальной теории относительности:

, ,
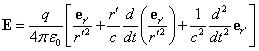
(11)

здесь − вектор от заряда до
удалённой точки в ранний момент времени ,

− единичный вектор,
направленный от заряда в удалённую точку, взятый для случая вращения этого
заряда по окружности в раннее время .

Формулы (11) впервые были опубликованы О. Хевисайдом в 1902 году. Затем
они были независимо переоткрыты Р. Фейнманом около 1950 года и использовались
им в лекциях как удобный способ описания синхротронного излучения [11].

Из определений и видно, что они взаимно
зависят друг от друга. Возьмём от них производные по времени:

, ,

а затем выразим эти производные независимо друг от друга:

, .

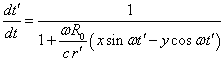
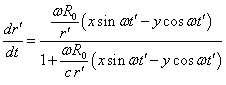
Если орбитальная скорость заметно меньше
скорости света , как это имеет место для электрона в атоме, то видно, что:

, . (12)

Беря первую производную по времени от единичного вектора первоначального
направления, находим:

, (13)

, .

Заменим в правой части (13) производные по времени на их максимальные
значения согласно (12) и вычислим вторые производные по времени от единичного
вектора:

.
(14)

Для компонент производной в (11) с учётом (12) и
(13) имеем:

. (15)

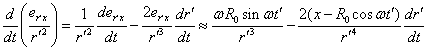
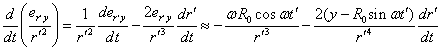
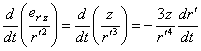
Подставляя (14) и (15) в (11), находим компоненту напряжённости
электрического поля :

(16)

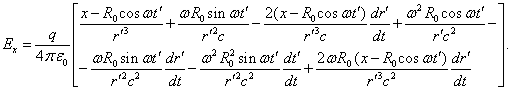
Согласно (12), , и тогда в (16) третий и седьмой члены меньше первого, так
как . Аналогично, с учётом соотношения пятый и шестой члены в
(16) всегда меньше, чем второй член. В результате, оставляя в (16) и в (11)
наибольшие члены, для компонент электромагнитного поля имеем:

.
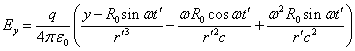
(17)

, ,

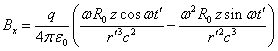
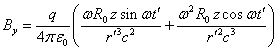
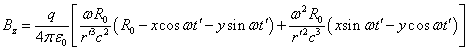
На больших расстояниях, при , в компонентах электрического поля (17) начинают преобладать
последние члены, содержащие в знаменателе , а в компонентах магнитного поля – члены, содержащие в
знаменателе .

Вектор Пойнтинга или поток электромагнитной энергии равен:

Если в (17) учитывать только последние члены, остающиеся на большом
расстоянии, то компоненты вектора Пойнтинга будут следующие:

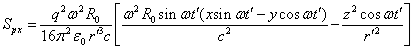
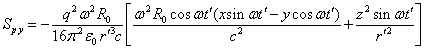
Мы должны вначале усреднить компоненты и за один период
вращения заряда, когда фаза меняется от 0 до . Учитывая, что , имеем:

, .

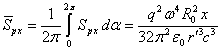
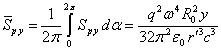
Интегрируя теперь по поверхности
удалённой сферы, находим усреднённую за период мощность потока электромагнитной
энергии:

. (18)

здесь есть единичный вектор,
перпендикулярный поверхности сферы, есть элемент площади,
для сферических координат , , и было принято, что .

Мощность излучения в (18) совпадает с результатом в (3), при этом для
расчёта вместо полных выражений для поля мы использовали только компоненты поля
из (17), остающиеся в удалённой зоне.

4. Формирование фотона

4.1. Ближняя зона

Электрон в атоме мы рассматриваем как плоский диск, центр которого
сдвинут относительно ядра и вращается вокруг ядра при излучении фотона. После
своего образования фотон становится самостоятельным объектом и перестаёт
зависеть от полей, создаваемых излучающим электроном и атомным ядром. Теперь
нам предстоит построить модель фотона, понять, из чего он состоит, как в нём
поддерживается перпендикулярная структура электромагнитного поля и почему фотон
является стабильным объектом. С этой целью обратимся к результатам в [12-13],
где фотон рассматривается как объект, состоящий из тесно связанных заряженных
частиц.

В качестве заряженных частиц, пронизывающих всё пространство в разных
направлениях и создающих силы взаимодействия между электрическими зарядами, в
[14] предполагаются положительно и отрицательно заряженные праоны. Эти частицы
составляют одну из компонент вакуумного поля, наряду с полем гравитонов,
ответственным за возникновение гравитационных сил [15] в модели Лесажа.
Найденное для праонов отношение массы к заряду оказывается как раз таким, какое
следует из коэффициентов подобия между разными уровнями материи и из теории
размерностей. Согласно теории бесконечной вложенности материи праоны составляют
вещество нуклонов так же, как нуклоны составляют вещество нейтронных звёзд. При
этом потоки заряженных праонов являются причиной силы Кулона, а внутри фотонов
праоны приходят в состояние устойчивого и упорядоченного вращения.

В субстанциональной модели электрона [9] в
атоме водорода в основном состоянии средний радиус электронного диска
принимается равным радиусу Бора , минимальный радиус диска составляет и максимальный радиус
достигает . Это радиусы коррелируют с распределением электронной
плотности согласно волновой функции электрона и решения уравнения Шрёдингера.
Вблизи ядра при радиусе меньшем, чем , плотность вещества
электрона быстро падает. Мы считаем, что потоки праонов проходят здесь вдоль
оси перпендикулярно
плоскости электронного диска без прямого контакта с веществом электрона,
взаимодействуя с ядром и электроном лишь посредством поля. Из симметрии полей
ядра и электронного диска следует, что вблизи оси потоки праонов
движутся в основном линейно, создавая основу излучаемого фотона. Другие праоны,
проходящие через электронный диск, после взаимодействия с заряженным веществом
диска включаются в оболочку фотона с сечением порядка размера электронного
диска. Такая же картина остаётся и для водородоподобного атома.

Для примера в [14] фотон рассматривался в первом приближении как длинный
тонкий цилиндр, вращающийся с угловой частотой , где есть длина волны
фотона. Для фотона с длиной волны м и угловой частотой с^-1, возникающего в атоме водорода при переходе
электрона со второго на первый уровень в серии Лаймана, в качестве
радиуса фотона принимался средний радиус электронного диска . Общая длина фотона определялась выражением , где есть длительность
излучения фотона атомом согласно (7).

Проанализируем компоненты электромагнитного поля в произвольной точке
пространства , координаты и которой не сильно
превышают радиус орбиты излучающего вращающегося
заряда, а координата такова, что по модулю
заметно больше, чем радиус орбиты: . В этой зоне выполняется условие , так что в (17) преобладают первые члены. Переходя к
водородоподобному атому, заменим ещё в (17) на отрицательный заряд
электрона , где есть элементарный
заряд, и добавим к (17) компоненты статического электрического поля от заряда атомного ядра,
расположенного в центре системы координат. Результат для компонент полей можно
записать так:

, , . (19)

, , .

Компонента магнитного поля в (19) осциллирует
сложным образом. Если мы ограничимся областью, в которой , то есть за пределами атома, но с условием ближней зоны , то можно положить и . В этом случае можно пренебречь компонентой , так как она будет меньше в раз, чем компоненты и .

Компоненты электрического поля, зависящие от множителя , определяют постоянное поле от эффективного заряда водородоподобного
атома, спадающее с расстоянием согласно закону Кулона. Это поле должно ускорять
заряженные праоны, меняя их энергию. Однако в возникающем фотоне число
положительных и отрицательных праонов приблизительно одинаково, обеспечивая
электронейтральность фотона. Эти праоны также сильно взаимодействуют между
собой и находятся в связанном состоянии. Тогда компонента при достаточно больших
расстояниях не будет влиять на
движение частиц в нейтральном в среднем фотоне.

В результате картина движущегося поля будет формироваться в основном теми
компонентами в , , и , которые зависят от времени. Вводя поперечные векторы и , из (19) для этих компонент находим:

, ,
(20)

где единичный вектор задаёт положение
вращающегося электрона в плоскости в раннее время .

Из (20) видно, что поперечные компоненты электрического и магнитного полей вращаются вокруг
оси с угловой частотой синхронно с вращением
вектора и с вращением
электрона в атоме. При этом компонента направлена в
пространстве так же, как радиус-вектор электрона в раннее время, а магнитное
поле направлено
противоположно.

Запишем уравнение движения отрицательно заряженных праонов во внешнем
электромагнитном поле и найдём форму их движения, используя общие уравнения
движения аналогично [16-17]. Уравнение движения относительно раннего времени определяется силой Лоренца:

, (21)

здесь – инвариантная масса отрицательно заряженного праона,

– фактор Лоренца,

– элементарный заряд для праонного уровня материи,

– вектор скорости частицы.

После
подстановки полей (20) в (21) для движения частиц имеем:

.
(22)

Учтём, что компоненты силы Лоренца в (22), содержащие в знаменателе , можно исключить из расчёта, так как они значительно меньше
компонент без скорости света. Из соотношения указанных компонент следует
условие . Скорость праонов вдоль оси достигает почти
скорости света, так что остаётся условие , соответствующее ранее принятому выражению для ближней зоны.
Вследствие этого приблизительное решение уравнений (22) для скорости движения
частиц имеет вид:

, , .

Что изменится, если при этих скоростях мы учтём, что в компонентах
электрического поля (19) присутствуют ещё постоянные члены, содержащие
множитель ? Если действием компоненты поля можно пренебречь, то
учёт постоянных членов в компонентах и приводит к появлению
дополнительной центростремительной силы. Эта сила действует на отрицательные
праоны и меняет их скорость на устойчивой траектории вращения до следующих
значений:

, , .

(23)

Для водородного атома и выражения для
скоростей упрощаются. В этом случае из (23) видно, что в ближней зоне при
времени , не превышающем периода вращения электрона вокруг ядра,
отрицательные праоны вращаются вокруг оси со скоростью вслед за вращением
электрона в атоме. У положительных праонов при том же векторе угловой скорости
компоненты линейной скорости в (23) будут противоположны по направлению
относительно компонент скорости отрицательных праонов, вследствие другого знака
заряда. Для такого движения достаточно,
чтобы отрицательные праоны вращались с той же стороны, что и электрон в раннее
время, а положительные праоны находились с противоположной стороны относительно
оси , при одинаковом общем вращении. Мы можем ещё учесть, что
отрицательные праоны на своём уровне материи являются аналогами электронов и
потому отношение масс положительных и отрицательных праонов равно отношению
масс протона и электрона: . Подстановка вместо в (23) приводит к
тому, что скорости движения и радиусы вращения у положительных праонов будут
существенно меньше, чем у отрицательных праонов.

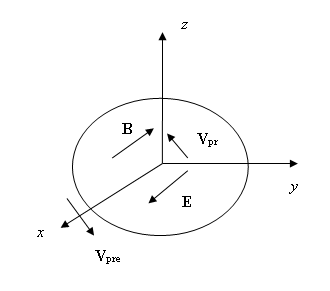
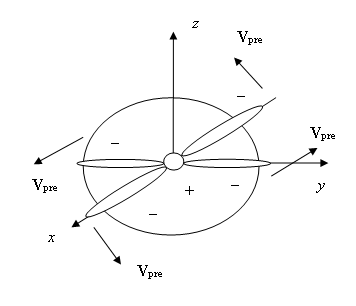
На рисунке 1 представлена поверхность, перпендикулярная оси и сдвинутая вдоль этой
оси на некоторое расстояние от атома, на которой изображены направления
электрического и магнитного поля (20) и скорости праонов согласно (23) для
водородного атома при . Все вектора соответствуют моменту времени , при котором выполняется условие , где . Вектор обозначает скорость
положительных праонов.

4.2. Волновая
зона

Рассмотрим теперь другой крайний случай, когда координата попадает в удалённую
волновую зону. Здесь свойства образующегося фотона должны проявиться в полной
мере. Если рассматривать компоненты электрической напряжённости поля в (17), то
видно, что из всех членов максимальными становятся члены, содержащие квадрат
скорости света. Эти члены медленно спадают с расстоянием, так как содержат в
знаменателе расстояние в первой степени. В
магнитных компонентах наибольшие члены также медленно спадают с расстоянием,
так как пропорциональны множителю .

Вновь переходя к водородному атому, заменим в (17) на отрицательный заряд
электрона , и добавим к (17) компоненты статического электрического
поля от заряда атомного ядра,
расположенного в центре системы координат. В результате компоненты поля в
волновой зоне можно выразить так:

, , .

(24)

, , .

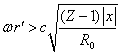
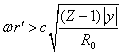
Будем рассматривать достаточно большие расстояния , когда выполняются условия , . Тогда в компонентах и в (24) можно будет
пренебречь постоянными членами от поля ядра. Что касается компоненты , то она должна слабо влиять на движение фотона ещё и ввиду
его электронейтральности.

Компонента магнитного поля по сравнению с
компонентами и мала. Например,
отношение амплитуд компонент и при небольших и оценивается величиной .

Далее будем считать, что компонента близка к нулю и в
волновой зоне не участвует в процессах внутри фотона. Тогда остающиеся в (24)
электрические и магнитные поля будут перпендикулярными друг другу и оси , причём компоненты магнитного поля сдвинуты вперёд
относительно компонент электрического поля на угол и вращаются с той же
частотой . Кроме этого, возникает соотношение . В фотоне выполняются аналогичные условия, и следует
ожидать, что поля вида (24) должны формировать фотон с круговой поляризацией,
то есть с вращением электрического вектора относительно оси фотона.

Перейдём в (24) от раннего времени к текущему времени в лабораторной системе
отсчёта, учитывая определение: . Введём ещё волновой вектор с амплитудой , направленный вдоль оси так, что при любом
знаке координаты и скорости праонов выполняются
соотношения: , . Тогда и для периодически
изменяющихся полей можно записать:

, ,

,
.
(25)

Как видно, при каждом постоянном значении поля в (25) зависят от
времени по синусоидальному закону. Кроме этого, по мере увеличения координаты в точках, где
выполняется условие , а , поля (25) вращаются синхронно друг с другом вдоль оси . Тем самым поле приобретает периодическую пространственную
структуру, повторяющуюся через минимальное расстояние, равное длине волны. В
предыдущем случае при решении уравнения (21), пространственная структура не
предполагалась, так как рассматривалась ближняя зона, размер которой находится
в пределах менее одной длины волны.

Аналогично (21), запишем уравнение движения отрицательных праонов, но уже
по отношению к текущему времени :

После
подстановки в это уравнение полей (25) имеем:

, (26)

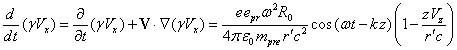
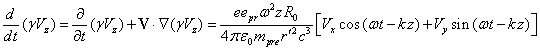
В правой части (26) сила Лоренца зависит от двух переменных – от времени и от координаты , задающей расстояние до излучающего атома. Поэтому при
движении заряженных частиц в электромагнитном поле ускорение и скорость частиц
также становятся функциями и . В связи с этим производные по времени в левой части (26) мы
представили как производные Лагранжа.

Изменение более существенно
сказывается в аргументе синусов и косинусов, чем при изменении в знаменателе
амплитуды. Если рассматривать как переменную лишь
внутри синусов и косинусов, то приблизительное решение уравнений (26) для
скорости движения частиц имеет вид:

, , .

(27)

Если зафиксировать время , то при изменении координаты от до вектор скорости в (27)
сделает полный оборот вокруг оси , причём при больших уменьшение амплитуды
скорости за счёт изменения будет невелико. Это
оправдывает наше приближённое решение (27), хотя мы и не учли при решении
уравнений изменение в в знаменателе
амплитуды силы Лоренца.

На рисунке 2 показана поверхность, перпендикулярная оси , на которой изображены направления электрического и
магнитного поля (25) и скорости праонов согласно (27). Вектора и обозначают скорости
положительных и отрицательных праонов, соответственно.

Отметим различие между решениями (23) и (27), заключающееся в том, что
скорости праонов в них для атома водорода при отличаются знаками. В
этом случае вблизи границы между ближней и волновой зонами, отражаемой условием
, происходит изменение действия поля. А именно, общее поле
электрона меняет свою фазу на противоположную, из-за усиления компонент поля
(25) по сравнению с компонентами поля (20). В результате, когда электрон
вращается с одной стороны от оси , отрицательные праоны сосредоточены и вращаются под
действием поля с противоположной стороны от оси . Что касается положительных праонов, то теперь они
сосредоточены с той стороны, где движется электрон, и вращаются с меньшей
скоростью и с меньшим радиусом вращения, благодаря своей большой массе.

Кроме этого, в волновой зоне у фотона появляется пространственная
структура. Как это можно объяснить физически? Предположим, что электромагнитное
поле электрона, периодически изменяющееся при его вращении, приходит в
некоторое сечение фотона на расстоянии от атома и приводит в
движение его частицы. Затем электрон делает оборот в атоме, и к этому моменту в
сечение при подходят со стороны
атома новые частицы фотона. Электрон воздействует на них своим полем, как в
предыдущем случае, и всё повторяется. Это же справедливо и для точек с
координатами , куда поле от электрона приходит в той же самой фазе и было
соответственно излучено электроном в более ранние моменты. С момента начала
излучения фотона по мере течения времени и увеличения количества оборотов
электрона количество однофазных точек с координатами растёт до тех пор,
пока вращающееся поле электрона не охватит всю ту область, которую должен
занимать фотон. Если ещё движение частиц внутри фотона происходит определённым
образом и синхронно с движением электрона, как в (27), то это и создаёт необходимые условия для волновой
структуры внутри фотона, периодически изменяющейся в пространстве и времени.

Компоненты скорости в (27) записаны в
системе отсчёта , связанной с излучающим фотон атомом. Перейдём теперь в
систему отсчёта , которая движется вдоль оси со скоростью , практически достигающей скорости света. Для этого
используем прямые преобразования Лоренца в следующем виде:

, , , ,

.
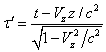
(28)

В мы обозначили
собственное время через , чтобы не было путаницы с ранним временем в (20). Нам также
понадобится преобразование скоростей, то есть связь между скоростями в обеих
системах отсчёта. В данном случае получается следующее:

, , ,

. (29)

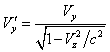
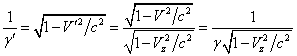
Скорость обозначает полную
скорость частицы в , а есть фактор Лоренца
частицы в . Подставим в (27) преобразование Лоренца для волновой фазы
(28) и преобразование (29) скоростей и фактора Лоренца, оставляя в амплитуде скорости
неизменной и выраженной через координаты в :

, . (30)

Как известно, роль преобразований Лоренца сводится к тому, чтобы
установить связь между показаниями часов и координатами событий в инерциальных
системах отсчёта. Из них следует, что в движущихся системах скорость хода часов
замедляется. В (30) в системе отсчёта с учётом соотношения и обратных
преобразований Лоренца в волновой фазе (28) роль угловой скорости вращения
вектора скорости играет величина 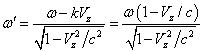. Угловая скорость меньше, чем угловая
скорость вращения электрона в атоме и
угловая частота фотона, как следствие эффекта замедления времени. Одновременно
с этим в волновой вектор становится меньше,

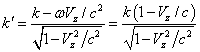
а длина волны больше, что связано с
эффектом сокращения продольных размеров движущихся тел в .

Согласно (30) в системе отсчёта наблюдается вращение
отрицательных праонов с угловой скоростью в плоскостях , а при мгновенном перемещении наблюдателя вдоль оси с изменением обнаруживается сдвиг
фазы вращения на величину . Для этого частицы внутри фотона должны быть расположены
так, что они как будто находятся на поверхности винта с правой резьбой с шагом , причём винт крутится вправо с угловой скоростью , не перемещаясь при этом вдоль оси . Если в качестве вращающихся частиц внутри фотона
рассматривать ещё положительные праоны, то ввиду их увеличенной массы их
скорость вращения в (30) будет меньше. Положительные праоны можно расположить
на поверхности винта, радиус которого в раз меньше радиуса
винта для отрицательных праонов. В каждый момент времени положительные праоны
находятся с той же стороны, что и электрон в соответствующее запаздывающее
время , а отрицательные праоны сосредоточены при этом с другой
стороны оси .

4.3. Вторая компонента поля

Рассмотрим действие второй компоненты поля в (17) на движение частиц
внутри фотона в волновой зоне. Поле этой компоненты при с учётом
электрического поля ядра имеет вид:

, , .

(31)

, , .

При условиях , в компонентах
электрического поля в (31) можно будет пренебречь постоянными членами от поля
ядра, содержащими . Кром этого, можно ещё пренебречь компонентой магнитного
поля , так как она будет меньше в раз, чем компоненты и . Перейдём в (31) от раннего времени к текущему времени , учитывая определение: . При находим:

, ,

,
.
(32)

Действуя так же, как в предыдущем разделе, имеем аналогично (26):

Приблизительное решение этих уравнений для скорости движения частиц имеет
вид:

, , .

(33)

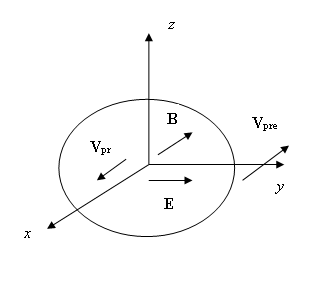
На рисунке 3 показана поверхность, перпендикулярная оси , на которой изображены направления электрического и
магнитного поля (32) и скорости праонов согласно (33). Все вектора соответствуют
моменту времени , при котором выполняется условие . Вектора и обозначают скорости
положительных и отрицательных праонов, соответственно.

5. Структура фотона

Наличие в знаменателе скорости
в (23) для ближней зоны и в (27) в волновой зоне приводит к уменьшению
амплитуды скорости по мере удаления от излучающего атома. Очевидно, что для
самостоятельного существования фотона при некотором расстоянии от атома
амплитуда скорости вращения отрицательно заряженных праонов в фотоне должна
перестать зависеть от . По аналогии с (20) и (25), в которых заменим на некоторое
постоянное расстояние , предположим следующие выражения для амплитуды
электрического поля внутри фотона в ближней и волновой зоне соответственно:

,
.

Мы имеем возможность оценить значение с помощью данных из [14]
для фотона с угловой частотой с^-1, возникающего в атоме водорода при переходе
электрона со второго на первый уровень в серии Лаймана, полагая радиус фотона
равным . Исходя из энергии фотона и его объёма, при равенстве
плотности этой энергии и плотности электромагнитной энергии определяется
амплитуда электрического поля внутри фотона: В/м.

Если приравнять и , то получится, что , где есть радиус Бора. Если
же приравнять и , то должно быть . В ближней зоне поле существенно меньше,
чем поле , и поэтому поле лишь при малом
расстоянии от ядра, порядка , способно привести в такое движение праоны фотона, чтобы в
нём могло быть поле порядка . На границе между ближней и волновой зонами, отражаемой
условием , значение . Следовательно, внутренняя электромагнитная энергия фотона,
связанная с движением в нём заряженных частиц, появляется у него уже в ближней
зоне. Здесь на частицы возникающего фотона действует электрическое поле (17),
состоящее из трёх основных компонент, которые выравниваются друг с другом при и значении .

Амплитуда поперечного электрического поля второй компоненты в (17)
согласно (32) при равна . Из равенства получается оценка: , так что в ближней зоне вторая компонента в (17) уступает
первой компоненте по степени влияния на частицы внутри фотона, но действует
сильнее третьей компоненты поля.

Анализируя направления полей и скоростей частиц на рисунках 1-3,
являющихся следствием компонент поля (17), можно построить в первом приближении
симметричную по форме модель фотона. Сечение фотона при в этой модели
представлено на рисунке 4.

Когда фаза вращения электрона в атоме удовлетворяет соотношению , где есть раннее время, для
каждого момента времени можно подобрать такие , где картина событий повторяется так же, как на рисунке 4.
При этом на рисунке 4 лепестки вдоль оси образуются
отрицательными праонами под действием полей вида (20) и (25), как на рисунках 1
и 2 соответственно. На рисунке 4 мы добавили также лепестки из отрицательных
праонов, которые вероятно могут возникать под действием полей (32), как на
рисунке 3. В центре вблизи оси сосредоточены
положительные праоны. Вся конструкция из лепестков вращается вокруг оси с угловой скоростью и ещё движется вдоль
этой оси со скоростью , практически равной скорости света. В заданный момент
времени при изменении меняется фаза и в новом сечении
фотона появляются другие лепестки, сдвинутые относительно лепестков на рисунке
4 на соответствующий угол. Это означает, что всё множество таких лепестков из
отрицательных праонов образуют непрерывные винтовые линии в пространстве с
шагом, равным длине волны, и длиной вдоль оси , равной длине фотона.

При этом можно ожидать, что при формирование двух
соответствующих лепестков заканчивается и они становятся независимыми от
спадающего по амплитуде поля . Для остальных лепестков то же самое следует при для поля и при для поля . Хотя эти оценки не совсем точные, так как мы предполагали
постоянство в знаменателе решений
для скоростей движения праонов (23), (27) и (33), общий результат остаётся
неизменным: электрическое поле вращающегося электронного облака способно
создавать лепестковую структуру возникающего фотона. Возникшие из праонов
лепестки затем фиксируются силами, действующими между праонами.

В принципе, внутри каждого лепестка на рисунке 4 должно быть достаточно
плавное распределение заряда, от положительного заряда в центре до преобладания
отрицательного заряда на концах лепестков. Это должно сопровождаться также
плавным изменением плотности массы вдоль лепестков. В этом случае лепестки
кроме отрицательных праонов содержат в себе и значительное количество
положительных праонов. Мы сопоставляем положительные праоны с протонами, а
отрицательные праоны с электронами, и допускаем существование нейтральных
праонов как аналогов нейтронов.

Из решений для скоростей движения праонов (23), (27) и (33) видно, что
эти скорости в первом приближении не зависят от того, в положительном или
отрицательном направлении оси распространяется
фотон. Эти решения не препятствуют тому, что в квантовом переходе из атома
будут одновременно излучаться сразу два фотона в противоположных направлениях.
Эти фотоны должны иметь противоположно направленную круговую поляризацию, то
есть различаться направлением вращения электрического вектора относительно
скорости фотона.

Однако как правило, за исключением
особых случаев возбуждения, многоэлектронный атом излучает один фотон. Для
объяснения этого обратимся к результатам в [9], где была представлена
субстанциональная модель электрона, рассматриваемого не как заряженная точка, а
как объёмная структура в виде электронного диска. Предполагается, что вещество
в диске вращается дифференциально вокруг центра диска с угловой скоростью , зависящей от текущего радиуса местоположения
элемента вещества. Кроме этого, центр диска имеет возможность находиться на
расстоянии от ядра и вращаться
вокруг него с угловой скоростью . Последнее позволяет объяснить спин электрона как результат
вращения электронного диска как целого вокруг ядра, и обеспечить возможность
электромагнитного излучения из атома, пока имеется вращение с угловой скоростью
. В [9] учитывается, что отрицательно заряженное вещество
электронного облака притягивается к положительно заряженному ядру и
одновременно отталкивается само от себя электрическими силами. В этой модели на
вещество также действует сильная гравитация от ядра с постоянной сильной
гравитации м³ ∙кг⁻¹ ∙с⁻². Сумма всех
этих сил заставляет вращаться вещество электрона вокруг ядра. Устойчивые
квантованные состояния энергии атома объясняются тем, что в данных состояниях
осуществляется равенство потока кинетической энергии вещества электрона и суммы
потоков электромагнитной и гравитационной энергий в этом веществе. При этом
излучение из атома стремится к нулю и состояние вращения электронного диска
остаётся неизменным длительное время, а импульс поля не передаётся веществу.

В субстанциональной модели электрона существенным для нас является то,
что в многоэлектронном атоме электронные диски в атомных оболочках
располагаются приблизительно параллельно друг другу и количество электронов в
каждой заполненной оболочке чётное. Это приводит к тому, что магнитная энергия
атома стремится к минимуму, так как у соответствующих спаренных электронов
магнитные моменты направлены противоположно (принцип Паули). Для объяснения
принципа Паули применяется известное правило Ленца: при увеличении магнитного
поля в проводнике в нём создаётся такое магнитное поле, которое
противодействует первоначальному магнитному полю. Если атом имеет неспаренный
электрон и соединяется со свободным электроном, в последнем вращение вещества в
диске будет таким, чтобы создать магнитное поле по правилу Ленца и в
соответствии с принципом Паули. Такое объяснение не требует ссылки на квантовые
спины электронов и опирается на известные электромагнитные явления.

Для максимального числа электронов в электронной оболочке атома
существует зависимость квадратичного вида . Для множителя 2
перед мы считаем, что это
следствие принципа Паули, а также симметрии при расположении электронов в виде
колец-дисков. Что касается квадратичной зависимости , то видно, что с увеличением номера оболочки растёт и расстояние до
этой оболочки. Площадь оболочки подобно площади сферы изменяется
пропорционально квадрату расстояния. Поэтому при соответствующем изменении
расстояния до оболочки с номером относительная плотность
электронов, как число электронов на единицу площади оболочки, остаётся
неизменной. Только в этом случае всё вещество каждого электрона будет с
одинаковой плотностью размещаться на каждой оболочке, а суммарные заряды и
массы электронов на оболочках будут целочисленны.

Рассмотрим теперь простейший случай, когда имеются два спаренных
электрона в виде двух параллельных дисков, причём один возбуждённый электрон
находится в состоянии квантового
перехода и уменьшает свой момент импульса с излучением фотона. Мы видим, что
ситуация для двух противоположных потоков праонов, проходящих через диск
возбуждённого электрона, несимметрична: один поток праонов проходит через
первый электрон и затем через второй, возбуждённый электрон. Другой поток
праонов проходит вначале через второй, а потом через первый электрон. Так как
первый электрон не возбуждён, центр его диска не сдвинут относительно ядра и не
вращается, электрон не излучает и влияет на поток праонов только своими
стационарными полями. Это приводит к небольшому сдвигу потока праонов, который
затем взаимодействует с веществом и полями возбуждённого электрона и включается
в формирование фотона в направлении распространения потока праонов.
Противоположный поток праонов вначале проходит через диск возбуждённого электрона
и в этом потоке возникает поперечное вращение праонов, необходимое в фотоне. Но
затем поток проходит через диск второго электрона, где поперечное вращение
праонов подавляется действием вращающегося заряженного вещества электрона,
затрудняя формирование фотона в этом направлении. Для атомной оболочки, где
число электронов более двух, ситуация усложняется, но принципиально не меняется
– для преимущественного излучения фотона из атома в одну сторону требуется
несимметрия расположения возбуждённого электрона относительно других
электронов.

6. Поля внутри
фотона

Отметим, что сами заряженные праоны не могут генерировать такое
электромагнитное поле внутри фотона, чтобы это поле в свою очередь приводило к
нужному движению частицы и удерживало их вместе. Для такого движения праонов
необходима либо дополнительная внешняя сила, например электромагнитная сила
Лоренца в (26) от поля вращающегося электрона в атоме, либо некоторая
внутренняя неэлектромагнитная сила. Для праонов внутри фотона мы предполагаем
действие сильной гравитации [14], которая должна действовать между положительно
заряженными праонами в сердцевине фотона и отрицательно заряженными праонами в
лепестках. Двумя другими силами являются электромагнитная сила притяжения между
противоположно заряженными праонами в сердцевине и в лепестках фотона и
электромагнитная сила отталкивания отрицательных праонов друг от друга. Праоны
в лепестках находятся в состоянии непрерывного вращения, поэтому следует ещё
учитывать центростремительную силу.

Ранее мы вывели постоянную сильной гравитации для уровня атомов,
приравняв по величине все четыре вышеуказанные силы, действующие на вещество
электрона в атоме водорода [9], [12]. Положим в первом приближении, что такое
же условие равенства величин сил справедливо и для праонов внутри фотона в
системе отсчёта , связанной с фотоном. Представим любой из лепестков в виде
некоторого конденсатора, одна обкладка которого заряжена положительно и
находится у оси , а другая обкладка заряжена отрицательно и находится на
конце лепестка. Мы полагаем, что фотон в целом нейтрален и количество
положительно и отрицательно заряженных праонов в нём одинаково. Обкладки
конденсатора притягиваются друг к другу электрической силой, а также силой
притяжения от сильной гравитации:

, ,

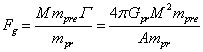
где и представляют собой
заряд и массу положительных праонов на той обкладке конденсатора, которая
примыкает к оси , произведение есть суммарная масса
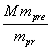
отрицательных праонов на другой обкладке конденсатора на конце лепестка, и задают массы
отрицательных и положительных праонов,

и есть напряжённость
электрического и соответственно напряжённость гравитационного поля, действующие
на обкладку с отрицательными праонами, обозначает площадь
обкладки конденсатора.

Из равенства сил и , а также условия , находим:

.
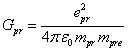
(34)

Заряд и масса положительного праона были найдены в [14] с помощью теории
размерностей и коэффициентов подобия между атомным и праонным уровнями материи: Кл, кг, здесь используются коэффициенты подобия по массе , по размерам и по скоростям
процессов . Подставляя заряд и массу праона в (34) с учётом соотношений
вида , , получаем оценку постоянной сильной гравитации: м³·кг^-1·с^-2. С другой стороны, постоянные гравитации на звёздном, атомном и праонном
уровнях материи согласно теории размерностей связаны друг с другом
коэффициентами подобия:

м³·кг^-1·с^-2, м³·кг^-1·с^-2,

при этом для постоянной сильной
гравитации на уровне атомов справедливо соотношение из [12], совпадающее по
смыслу с (34):

Постоянная сильной гравитации позволила не только
описать устойчивость электронов в атоме, но и объяснить сущность энергии покоя
элементарных частиц, вывести формулу для
магнитного момента протона [9] и вычислить его радиус [18]. Объясняется
также устойчивость нуклонов в ядре атома, при этом притяжению сильной
гравитации между нуклонами противостоит сила отталкивания полей кручения
сильной гравитации нуклонов (спин-спиновое взаимодействие в гравитационной
модели сильного взаимодействия). Константа связи сильной гравитации близка по
величине к стандартной константе связи сильного взаимодействия. В [15] было
показано, что структура сильной гравитации такая же, как и у обычной
гравитации, а диапазон действия сильной гравитации в веществе, имеющем
плотность массы как у Земли, не превышает 0,7 м [9].

Таким образом можно утверждать, что сильная гравитация на уровне праонов
и электромагнитные силы способны удержать друг возле друга положительные и
отрицательные праоны внутри фотона и обеспечить целостность фотона. Что
касается устойчивости положительных праонов, сосредоточенных в основном в
сердцевине фотона, то здесь основными силами становятся гравитационные силы
притяжения и силы отталкивания праонов друг от друга согласно гравитационной
модели сильного взаимодействия [9]. В этой модели силе гравитации противостоят
спиновые силы от поля гравитационного кручения, что позволяет обеспечить, в том
числе, стабильность атомных ядер.

На рисунке (4) электрическое поле внутри лепестков направлено наружу от
оси . В фотоне кроме электрического поля должно быть магнитное
поле, направленное перпендикулярно электрическому полю. Чтобы понять, как
возникает такое магнитное поле, рассмотрим вращение лепестков фотона на рисунке
4 с точки зрения системы отсчёта , как в разделе 4.2. Эта система отсчёта движется вдоль оси с той же скоростью , что и сам фотон в системе отсчёта . Учитывая (29), в в каждом сечении
фотона лепестки вращаются вокруг оси с угловой скоростью:

.
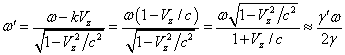
(35)

В (35) означает близкий к
единице фактор Лоренца для праонов в системе отсчёта , а есть очень большой по
величине фактор Лоренца для праонов в системе отсчёта , в которой полная скорость и скорость праонов близки к
скорости света. В [14] была сделана оценка фактора Лоренца для праонов в
фотоне: . Значение получается существенно
меньше, чем , характеризуя эффект замедления времени. Внутри лепестков
действует некоторое электрическое поле , находящееся в равновесии с напряжённостью поля сильной
гравитации и поддерживающее форму лепестков с учётом их вращения.

Рассмотрим преобразование электромагнитного поля лепестков из системы
отсчёта в систему отсчёта . Компоненты электромагнитного поля являются компонентами
тензора электромагнитного поля и потому преобразуются из одной инерциальной
системы отсчёта в другую как компоненты не 4-вектора, а 4-тензора. В частности,
для преобразования компонент поля при движении системы отсчёта вдоль оси можно записать:

, , ,
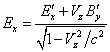
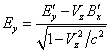
(36)

, ,

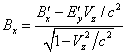
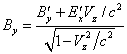
Медленное вращение отрицательно заряженных лепестков создаёт некоторое
общее магнитное поле . Рассмотрим на рисунке 4 один из лепестков, в котором внутреннее
электрическое поле в данный момент направлено вдоль оси и равно . В указанный момент времени усреднённые по объёму лепестка
другие компоненты электрического поля равны нулю, и , аналогично компоненты магнитного поля и . Тогда из (36) следует, что для усреднённых по объёму
компонент поля лепестка в системе отсчёта должно быть:

, , , , , .

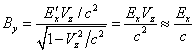
Так как , мы приходим к условию
, которое выполняется в фотоне и связывает между собой его
напряжённость электрического поля и магнитное поле. При этом поперечное
магнитное поле возникает как
следствие трансформации компонент электромагнитного поля из системы отсчёта в систему отсчёта , в которой фотон движется со скоростью . В каждой точке рассматриваемого лепестка в появляется магнитное
поле , перпендикулярное электрическому полю внутри этого лепестка.

Если на рисунке 4 взять другой лепесток,
то направление магнитного поля, пересекающего этот лепесток, соответственно
изменится, но будет перпендикулярно оси лепестка и его внутреннему
электрическому полю. В первом приближении можно полагать, что электрические
поля в сечении фотона на рисунке 4 вращаются вместе с лепестками и направлены
радиально от оси, а магнитное поле сосредоточено на отрезках окружностей в
местах, пересекающих лепестки, и направлено вдоль касательных к окружностям.

7. Фактор
Лоренца и потоки энергии

Напомним, как в [14] мы нашли отношение заряда к массе и фактор Лоренца для праонов в фотоне.
Пусть некоторый праон находится на радиусе и вращается с
некоторой скоростью вокруг оси фотона. Для
периода вращения частицы можно записать:

, .

Связь между
центростремительной силой, требуемой для вращения частицы, и электрической
силой, действующей на частицу с зарядом и массой покоя , следующая:

. (37)

Для фотона предполагается, что половину его энергии составляет энергия
вращения частиц, а другая половина энергии есть суммарная энергия всех полей. При
этом в системе отсчёта момент импульса фотона
равен постоянной Дирака и выражается формулой, которая соответствует
вращающемуся цилиндру, составленному из частиц:

. (38)

Исходя из (38), можно оценить энергию вращения: .

Разделив энергию фотона на объём фотона, получим плотность энергии, которую
можно приравнять к удвоенной плотности электромагнитной
энергии внутри фотона:

.
(39)

Из (37) и (39) для рассматриваемого фотона с учётом (7) при радиусе фотона и с^-1, следует:

Кл/кг. (40)

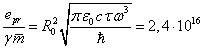
В разделе 6 мы показали, как из теории подобия уровней материи с помощью
коэффициентов подобия вычисляются заряд и масса праона. Если в (40) подставить , то отсюда находится значение фактора Лоренца .

Для случая водородоподобного атома можно видеть, что в (40) справедливы
пропорции: согласно (7), а также и . Если главные квантовые числа энергетических состояний и достаточно большие,
причём выполняется условие , то будет . Следовательно, фактор Лоренца растёт пропорционально
зарядовому числу ядра или пропорционально
квадратному корню из энергии фотона: . Наибольшее значение у фотона ожидается в
водородоподобном атоме, имеющим ядро с наибольшим количеством протонов, и для
электронных переходов вблизи наименьших орбит. В этом случае на праоны
возникающего фотона действуют наибольшие поля атома, передавая им свою энергию.

Из преобразований компонент электромагнитного поля (36) было найдено, что
в фотоне . При получении (34) мы исходили из того, что в фотоне
осуществляется баланс между электромагнитной силой и силой от сильной
гравитации, а в (37) учли ещё равенство электромагнитной силы и центростремительной
силы, возникающей от вращения праонов внутри фотона. В полный баланс сил
следует включить четвёртую силу, возникающую от расталкивания зарядов праонов
друг от друга. Все четыре силы приблизительно одинаковы по величине. Рассмотрим
теперь соотношение потоков энергии внутри фотона. Для средних значений
электромагнитного вектора Пойнтинга и соответственно гравитационного вектора
Хевисайда [12], [19], после усреднения за период волны периодически
изменяющихся компонент поля, можно записать:

, , , ,

здесь есть вектор поля
гравитационного кручения как компонента поля сильной гравитации, подобная по
смыслу индукции магнитного поля, и мы использовали условия вида и для амплитуд компонент
полей.

Вычислим отношение амплитуды среднего значения вектора потока
гравитационной энергии к амплитуде среднего значения вектора потока
электромагнитной энергии. Мы снова рассмотрим модель лепестка внутри фотона в
виде конденсатора, как при выводе (34), и учтём выражения для амплитуд
напряжённостей полей в виде: и . С учётом соотношения и (34) это даёт:

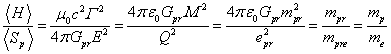
Отношение потоков гравитационной и электромагнитной энергии в фотоне
получается равным отношению массы протона к массе электрона. Это коррелирует с
тем, что согласно [14] для каждого уровня материи отношение плотности энергии
поля гравитонов в вакуумном поле, ответственных за гравитационные силы, к
плотности энергии поля заряженных частиц в вакуумном поле, ответственных за
электромагнитные силы, также равно отношению массы протона к массе электрона.

8. Дипольный
магнитный момент

Ненулевая компонента магнитного поля внутри фотона приводит
к тому, что фотон в целом должен иметь некоторый дипольный магнитный момент.
Рассмотрим фотон в системе отсчёта , в которой амплитуда волнового вектора и длина волны с
учётом (29) выглядят следующим образом:

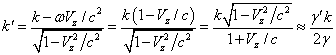
, . (41)

Для оценки магнитного поля представим фотон в системе отсчёта в виде соленоида
длиной , содержащего витков. В
сопутствующей фотону системе отсчёта в каждом таком витке
протекает ток . Здесь есть длительность
излучения фотона из атома, обозначает число
частиц, несущих заряд праона в одном витке, а
произведение задаёт общее количество
зарядов, участвующих в создании магнитного поля.

Масса в (38) является
некоторой эффективной массой и близка к массе праона ; различие этих масс связано с тем, что фотон не сплошной
цилиндр, а винтовая структура. Кроме того, сечение фотона на рисунке 4 имеет
вид лепестков, причём плотность массы в лепестках должна быть функций
расстояния от оси . В системе отсчёта момент импульса
записывается аналогично (38) и с учётом (35) и (38) имеем:

. (42)

Магнитное поле внутри длинного соленоида зависит только от числа витков
на единицу длины и от протекающего
тока :

Подставляя сюда , используя (35) и (41), а также выражая через из (42), находим:

. (43)

Если подставить сюда данные для рассматриваемого нами фотона:, , с, , Кл, и вместо использовать массу
праона кг, то получится оценка продольного магнитного поля внутри
фотона: Тл.

Магнитное поле в системе отсчёта связано с некоторым
эффективным током в витках соленоида,
которым моделируется фотон:

Мы вводим в рассмотрение эффективный ток потому, что заряженные праоны в не просто вращаются
вокруг оси , но ещё и летят вдоль этой оси со скоростью . С учётом этого, соотношения и (43), в
предположении, что , находим незначительный по величине дипольный магнитный
момент фотона в системе отсчёта :

А·м².
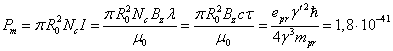
(44)

Если отрицательные праоны движутся так, как указано на рисунке 4, а фотон
распространяется в положительном направлении оси , то магнитный момент фотона получается направленным в
отрицательном направлении оси и противоположно
скорости фотона. Если же фотон распространяется против оси , то направления магнитного момента и скорости фотона будут
совпадать.

Отношение магнитного момента рассматриваемого фотона к магнетону Бора
получается равным . Заметим, что в [20], основываясь на астрофизических данных,
даётся ограничение на дипольный магнитный момент фотона, который не должен
превышать . В предыдущем разделе
мы нашли, что фактор Лоренца растёт пропорционально
зарядовому числу ядра в водородоподобном
атоме или пропорционально квадратному корню из энергии фотона: . Тогда из (44) следует, что фотоны малых энергий имеют
увеличенный магнитный момент. Кроме этого, магнитный момент фотона должен
увеличиться при переходах с большими квантовыми числами , соответствующими удалённым от ядра орбитам электрона.

В [9] изучалась структура различных нейтрино и способы их возникновения,
при этом было показано, что мюонные и электронные нейтрино содержат в себе
потоки одних и те же частиц (электронных нейтрино праонного уровня материи) и
отличаются друг от друга спектром энергии и способом упорядочения
(спиральностью) моментов импульса как этих частиц, так и их потоков в
пространстве. Благодаря этому электронные и мюонные нейтрино могут частично
переходить друг в друга. Нейтрино возникают в процессах слабого взаимодействия
и отличаются от фотонов своей внутренней структурой. Фотоны рождаются чаще
всего при взаимодействии потоков праонов вакуумного поля с ускоренным веществом
лептонов, а нейтрино более свойственны процессам внутри вещества адронов.

Несмотря на различие структур фотона и нейтрино, мы предполагаем, что
нейтрино атомного уровня материи, как и фотоны, состоят из праонов и обладают
магнитным моментом. В связи с этим приведём оценки дипольного магнитного
момента нейтрино: не более, чем согласно [21]; не
более, чем согласно [22]; не
более, чем согласно [23]. Как
видно, дипольный магнитный момент (44) для фотона в атоме водорода не превышает
значений, что ожидается для нейтрино.

9. Масса фотона

В специальной теории относительности известна формула, связывающая
релятивистскую энергию , импульс и инвариантную массу (массу покоя) частицы:

.
(45)

В [24] даётся ограничение на массу покоя фотона: эВ/c² в энергетических единицах,
а в [25] принимается, что эВ/c². Как правило, полагают,
что масса покоя фотона равна нулю, , и тогда энергия фотона зависит только от его импульса: . Последнее соотношение позволяет найти импульс фотона через
энергию или угловую частоту фотона. Фотон же при этом должен двигаться со
скоростью света .

Рассмотрим ситуацию с массой фотона в субстанциальной модели, описанной
выше. Из (38) можно определить релятивистскую энергию частиц внутри фотона,
умножая число праонов на среднюю массу покоя одной частицы , на фактор Лоренца и на квадрат скорости света:

. (46)

В (46) обозначает угловую
частоту фотона, есть энергия фотона, а
произведение по смыслу есть
усреднённая скорость вращения электрона в атоме при излучении фотона.
Следовательно, релятивистская энергия праонов в раз превышает энергию
фотона. По порядку величины, отличие энергий и достигает десятков
тысяч и более.

Инвариантная масса фотона, понимаемая как инвариантная масса праонов,
входящих в состав фотона, с учётом (46) равна:

.
(47)

Подставляя в (46) и в (47) данные для фотона, излучаемого атомом водорода
при переходе электрона со второго на первый уровень в
серии Лаймана: с^-1, , , получаем следующие оценки: Дж или 170 кэВ, кг или эВ/c²
в энергетических единицах. Получается, что масса покоя частиц фотона нулю не равна, хотя и
достаточно мала.

В (40) было найдено, что , при этом и . Следовательно, , то есть суммарная масса покоя частиц излучаемого фотона
увеличивается для атомных переходов с большими квантовыми числами и достигает максимума
для атома водорода с зарядовым числом ядра .

Вместо (45) для фотона можно записать:

.
(48)

Поскольку энергия покоя частиц фотона очень мала, в (48)
релятивистская энергия частиц фотона близка к произведению
импульса на скорость света: . Это связано с тем, что фактор Лоренца частиц внутри фотона
очень велик.

Из изложенного видно, почему в (48) масса покоя частиц фотона не равна нулю, тогда
как в (45) масса фотона приравнивается нулю.
Это вытекает из различия энергий и – если энергия связывается только с
энергией вращения праонов внутри фотона и с энергией их полей, то в энергии учитывается ещё
энергия движения праонов со скоростью , почти достигающей скорости света. Эта дополнительная
энергия не передаётся праонам от электрона при излучении фотона из атома, но
уже была у них в момент взаимодействия потоков праонов с электроном. Не учёт в
энергии начальной энергии праонов приводит к потере их массы покоя и
к обнулению массы в (45) для фотона. Кроме
этого, возникает и различие импульса праонов в (48) и общепринятого
импульса фотона в (45).

Несмотря на то, что вычисленная нами масса покоя частиц фотона существенно превышает
оценки массы фотона в [24] и в [25], масса прямо не
обнаруживается в экспериментах. Это связано с тем, что при взаимодействии
фотона с веществом происходит передача веществу момента импульса фотона
величиной порядка и соответствующей
энергии и импульса. Однако основная доля энергии фотона, заключённая в
релятивистском движении праонов, уносится вместе с ними в момент распада фотона
и рассеянии его на отдельные праоны.

Мы предполагаем, что скорости потоков праонов в
вакуумном поле порядка скорости света, . При этом фотоны движутся со скоростью , причём должно быть . Некоторое различие и объясняется тем, что
праоны в фотоне не только движутся вдоль оси , перпендикулярной плоскости электронного диска в момент
излучения фотона, но ещё и вращаются вокруг этой оси по некоторым спиралям.
Вращение праонов зависит от частоты фотона и его энергии, что должно влиять на
скорость движения фотонов и приводить к
некоторой изначальной дисперсии скоростей фотонов разных частот.

10. Заключение

В разделе 2 мы показываем, что частота излучаемого из атома фотона равна
частоте вращения центра электронного облака вокруг ядра, усреднённой за время
излучения фотона при квантовом переходе электрона из некоторого состояния в
состояние с меньшей энергией.

В разделе 3 мы приводим выражения для напряжённости электромагнитного
поля в волновой зоне вдали от заряда, вращающегося вокруг некоторого центра, с
помощью которых можно оценить поток электромагнитной энергии. Из них следует,
что основная часть энергии излучается от заряда в направлении оси вращении. В
других направлениях поток энергии достаточно быстро уменьшается по величине и
носит осциллирующий характер, не давая заметного излучения.

Взяв за основу электромагнитные поля в ближней и волновой зонах от
испытывающего квантовый переход водородоподобного атома, мы оцениваем действие
этих полей на заряженные частицы (праоны) вакуумного поля. Электрон в
субстанциональной модели электрона [9] рассматривается как диск, и указанные
поля приводят потоки праонов во вращение вокруг оси, перпендикулярной
электронному диску. Исходя из картины поля в разделе 4, в разделе 5 мы
представляем соответствующую структуру фотона. Положительно заряженные праоны
сосредоточены вблизи оси фотона, а отрицательно заряженные праоны образуют
винтовую часть фотона. Опираясь на эту структуру, мы с помощью идеи сильной
гравитации на уровне праонов решаем проблему устойчивости для положительно и
отрицательно заряженных праонов внутри фотона, объясняя долговременную
стабильность фотона огромной величиной постоянной сильной гравитации . Вращение отрицательных праонов внутри фотона приводит к
тому, что фотоны могут легко взаимодействовать с электронами и другими
заряженными частицами, обмениваясь с ними своей энергией.

Фотон излучается вдоль оси электронного диска, но некоторая часть энергии
в виде электромагнитного излучения уходит из возбуждённого атома по другим
направлениям. Это излучение находится в фазе с колебаниями внутри фотона.
Последнее может объяснить результаты опыта Юнга с малой интенсивностью света,
когда наблюдается интерференция у практически одиночных фотонов. В этом случае
каждый фотон проходит через ту или иную щель, а сопутствующее ему когерентное
излучение из атома проходит через другую щель, давая в итоге интерференционную картину.

В разделах 6-8 мы оцениваем значения полей внутри фотона, фактор Лоренца
для праонов и потоки энергии, вычисляем продольное магнитное поле и дипольный
магнитный момент фотона. При этом мы используем преобразования Лоренца для
перехода в систему отсчёта, движущуюся синхронно с фотоном.

Построение субстанциональной модели фотона мы завершаем рассмотрением
вопроса об инвариантной массе фотона, которая в специальной теории
относительности полагается равной нулю. В противоположность этому, в
субстанциональной модели мы вычисляем массу покоя праонов, образующих фотон,
которая очевидно не может быть равной нулю. С помощью этой массы и суммарного
импульса праонов определяется релятивистская энергия указанных праонов, которая
в десятки тысяч раз превышает энергию фотона в классической теории. Различие
этих энергий объясняется тем, что в общепринятую энергию фотона не включается
релятивистская энергия праонов, движущихся практически со скоростью света. В
результате в нашей модели фотон описывается стандартной релятивистской
формулой, связывающей его энергию, импульс и ненулевую массу покоя.

В обычной интерпретации фотон полагается элементарной частицей,
являющейся квантом электромагнитного излучения, уникальность которой
подчёркивается отсутствием массы покоя. В квантовой электродинамике фотон
является ещё калибровочным бозоном, при
этом переносчиком электромагнитного взаимодействия считаются виртуальные
фотоны. Однако в [14] мы показали, что электромагнитные силы могут возникать
под действием на заряженные тела многочисленных потоков праонов, существующих в
вакуумном поле. В данной статье мы рассматриваем процессы при квантовых
электронных переходах в атоме, которые позволяют формировать фотоны из потоков
праонов. Таким образом, концепция праонов позволяет не только понять устройство
фотона и найти его массу, но и дать общее объяснение основным электромагнитным
явлениям.

Если фотон имеет ненулевую массу, то как это изменяет наше понимание
эффекта отклонения света массивными телами под действием гравитации? Согласно
[15], гравитация объясняется в модели Лесажа как результат действия на тела
потоков гравитонов в вакуумном поле. В совокупности вакуумное поле состоит из
двух компонент, поля гравитонов и поля заряженных праонов, генерирующих
гравитационные и электромагнитные силы, соответственно. Фотон представляет
собой объект, составленный из праонов, тесно связанных посредством сильной
гравитации и электромагнитных сил. Потоки праонов вблизи массивных тел
отклоняются от своего движения под действием поля гравитонов. При этом фотон не
просто поток праонов, он несёт дополнительную энергию и момент импульса,
полученные в момент излучения. Двигаясь с релятивистской скоростью, фотон
должен испытывать действие поля гравитонов так же, как это поле действует на
другие частицы, имеющие ту же скорость. Например, в ковариантной теории
гравитации [9] полный угол отклонения определяется формулой: , где есть масса тела, и обозначают скорость и
прицельное расстояние релятивистской частицы на бесконечности. Если для фотона
положить , то мы приходим к формуле вида , справедливой для фотона, в том числе и в общей теории
относительности. В данной формуле нет зависимости от массы релятивистской
частицы или от массы фотона. Поэтому появление у фотона массы покоя изменит
полный угол отклонения на очень малую
величину, возникающую от различия скорости фотона и скорости света.

Субстанциональная модель даёт своё решение корпускулярно-волнового
дуализма фотона. В качестве оценки количества праонов в используемом нами
фотоне, излучаемого в атоме водорода, вычислим отношение: праонов. Всё это
множество праонов тесно связано с помощью электромагнитных сил и сильной
гравитации на уровне праонов, обеспечивая целостность и долговременную
стабильность фотона как частицы. С другой стороны, в силу своего возникновения,
фотон представляет собой длинную и вращающуюся в пространстве периодическую
структуру малого сечения. Благодаря этой структуре фотон и проявляет волновые
свойства, в том числе посредством своих периодически изменяющихся в
пространстве и времени напряжённостей полей.

Из изложенного следует также, что благодаря небольшому отличию скорости
фотона от скорости света,
регистрируемая скорость фотона будет неодинакова для наблюдателей в системах
отсчёта, движущихся с различными скоростями. В частности, предполагается
существование системы отсчёта , в которой продольная скорость фотона как целого равна нулю,
и остаётся лишь его собственное вращение.

Удобно считать, что скорость света является предельной величиной для
движения фотонов и частиц. При переходе к низшим уровням материи (к нуклонам,
праонам и т.д.) увеличивается фактор Лоренца у частиц, составляющих фотоны
соответствующего уровня материи, при этом скорости их движения не должны
превышать скорости света. Так применяется теория относительности в теории
бесконечной вложенности частиц. С другой стороны, если протон разгоняется
электромагнитными силами, а фактически с помощью направленных и
концентрированных потоков заряженных релятивистски движущихся праонов, то
скорость протона не сможет превысить скорость этих праонов. Если любой фотон и
образующие его праоны движутся со скоростью, меньшей скорости света, то и
скорость протона, ускоряемого с помощью таких праонов, не сможет достигнуть
скорости света. Релятивистские праоны, в совокупности образующие поле
заряженных частиц вакуумного поля, получили свою энергию в электромагнитных
полях вблизи протонов и других заряженных частиц. Лишь электромагнитное поле
является основным источником релятивистских заряженных частиц на всех уровнях
материи, и тогда получается, что все эти частицы движутся медленнее скорости
света.

Согласно теории бесконечной вложенности материи, вычисленные с помощью
коэффициентов подобия инвариантная масса положительно заряженного праона должна
быть кг, а радиус м при радиусе протона м согласно [18]. По видимому, в современных экспериментах
отдельные частицы столь малых масс и размеров не могут быть обнаружены
непосредственно. Действительно, поиски преонов как частиц, составляющих кварки
и лептоны, и партонов как составных частиц в нуклонах, в экспериментах по
рассеянию частиц дошли лишь до размеров м. Это много больше, чем ожидаемые размеры праонов. В
результате партоны были идентифицированы с кварками и глюонами, а преоны как
какие-то новые частицы не были обнаружены и остаются предметом теоретических
изысканий [26].

По нашему мнению, максимально возможная энергия фотона , а также инвариантная масса его частиц , существенно зависят от способа образования фотона. Если в
(39) удвоенную плотность электромагнитной
энергии внутри фотона приравнять к плотности энергии заряженных частиц
вакуумного поля , и взять из [14] значение Дж/м³,
можно оценить максимальную амплитуду напряжённости электрического поля внутри
фотона:

В/м.
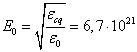
(49)

В (49) предполагается, что заряженные
частицы вакуумного поля (праоны) входят в состав фотонов в момент их
образования, причём плотность энергии фотонов не может превысить
плотность энергии . Последнее вытекает из того, что связано с вращением
праонов внутри фотона, когда скорость вращения не превышает скорости света, а есть усреднённая
плотность энергии праонов при их движении со скоростью порядка скорости света.
Напряжённость электрического поля (49) можно сравнить только с напряжённостью
поля на поверхности протона, у которого В/м.

Следовательно, образование фотонов больших энергий может быть связано с
релятивистскими протонами и взаимодействиями с ними, как это имеет место с
космическими лучами.

В [15] мы оценили температуру поля гравитонов, являющегося частью
вакуумного поля, для случая, когда гравитонами являются частицы типа фотонов: К. Предположим, что поле заряженных частиц вакуумного поля
имеет ту же температуру, что и поле гравитонов, и оба поля находятся в
температурном равновесии. Полагая в первом приближении справедливым закон
смещения Вина для длины волны , которую имеют большинство фотонов при данной температуре , с постоянной Вина м·К находим:

, Дж.

В энергетических единицах средняя энергия
фотонов получается равной ГэВ и принадлежит
диапазону гамма-квантов. Если исходить из того, что в (37-38) вместо радиуса можно подставить
радиус протона , а также использовать скорость света как предельную скорость
вращения праонов в фотоне: , то для максимальной энергии такого фотона находим: ГэВ.

Однако измерения показывают, что энергия фотонов может быть значительно
больше и достигать 80 ТэВ [27]. По всей видимости, фотоны таких энергий
образуются не в условиях температурного равновесия между веществом и
электромагнитным полем, а в существенно неравновесных условиях. Для этого
необходимо взаимодействие релятивистской частицы сразу с множеством частиц.
Примерами являются синхротронное излучение заряженной частицы в магнитном поле
достаточно большого и замагниченного объекта, а так же обратный эффект Комптона.

Список использованных
источников

1.
R.
Nisius. The photon structure from deep inelastic electron photon scattering.
Physics Report, 332,165 (2000). http://dx.doi.org/10.1016/S0370-1573(99)00115-5.

2.
T.
Yarman, C. Yesilyurt and M. Arik. A Novel Photon Model – Featuring an Internal
Dynamics along with an Amplitude of the Oscillating Particle of Light. Acta
Physica Polonica A 125 (2), 638 (2014). http://dx.doi.org/10.12693/APhysPolA.125.638.

3.
Masroor
H. S. Bukhari. A phenomenological model for photon mass generation in vacuo.
International Journal of Physical Sciences. 9 (4), 48 (2014). http://dx.doi.org/10.5897/IJPS2013.4025.

4.
Hongrui
Li. Continuing research on the classical spiraling photon model. Proc. SPIE 9277,
(2014). http://dx.doi.org/10.1117/12.2070574.

5.
I.
Bersons. Soliton Model of the Photon / Fotona Solitona Modelis. Latvian Journal
of Physics and Technical Sciences. 50 (2), 60 (2013). http://dx.doi.org/10.2478/lpts-2013-0013.

6.
P. Kamenov and B. Slavov. A Soliton-like Model for the Photon. Bulgarian
Journal of Physics. 23, 116 (1996).

7.
G. Hunter and R.L.P. Wadlinger. Photons and Neutrinos as Electromagnetic
Solitons. Physics Essays. 2, 158 (1989).

8.
Melike B. Yucel and Nuri Unal. First quantized electron and photon model
of QED and radiative processes. Can. J. Phys.
80 (8), 803 (2002). http://dx.doi.org/10.1139/p02-027 .

9.
Федосин С.Г. Физические теории и бесконечная вложенность
материи. Пермь,
2009, 842 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

10.
Landau, L.D., Lifshitz E.M. (1975). The Classical Theory of Fields (Vol.
2, 4th ed.). Butterworth-Heinemann.

11.
Feynman R, Leighton R, and Sands M. The Feynman Lectures on Physics. Volume 2. Mainly electromagnetism and matter. Addison-Wesley, Reading, MA. 1966.

12.
Федосин С.Г. Физика и философия подобия
от преонов до метагалактик. Пермь, Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93,
Библ. 377 назв. ISBN 5-8131-0012-1.

13.
Fedosin S.G. Cosmic Red Shift, Microwave Background, and New Particles. Galilean Electrodynamics, 2012, Vol. 23, Special Issues No. 1, P. 3 – 13. // Красное
смещение и космическое микроволновое фоновое излучение как следствие
взаимодействия фотонов с новыми частицами.

14.
Fedosin S.G. The charged component of
the vacuum field as the source of electric force in the modernized Le Sage’s model.
Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, P. 971-1020 (2016). http://dx.doi.org/10.4314/jfas.v8i3.18. // Заряженная компонента вакуумного поля как
источник электрической силы в модернизированной модели Лесажа.

15.
Fedosin S.G. The graviton field as the source
of mass and gravitational force in the modernized Le Sage’s model. Physical Science International Journal. Vol. 8, Issue 4, P.
1-18 (2015). http://dx.doi.org/10.9734/PSIJ/2015/22197. // Поле
гравитонов как источник гравитационной силы и массы в модернизированной модели
Лесажа.

16.
Fedosin S.G. Four-Dimensional Equation of
Motion for Viscous Compressible and Charged Fluid with Regard to the
Acceleration Field, Pressure Field and Dissipation Field.
International Journal of Thermodynamics. Vol. 18 (No. 1), P. 13-24, 2015. http://dx.doi.org/10.5541/ijot.5000034003. // Четырёхмерное уравнение движения вязкого сжимаемого
заряженного вещества с учётом поля ускорений, поля давления и поля диссипации.

17.
Fedosin S.G. The Hamiltonian in Covariant Theory of Gravitation. Advances in Natural
Science, 2012, Vol. 5, No. 4, P. 55 – 75. http://dx.doi.org/10.3968%2Fj.ans.1715787020120504.2023; Гамильтониан в ковариантной теории гравитации.

18.
Fedosin S.G. The radius of the
proton in the self-consistent model. Hadronic Journal, 2012, Vol. 35, No. 4, P. 349 – 363. // Радиус протона в самосогласованной модели.

19.
O. Heaviside (1893). A gravitational and electromagnetic analogy. The
Electrician 31: 81–82.

20.
Brett Altschul. Astrophysical bounds on the photon charge and magnetic
moment. Astroparticle Physics, 2008, Vol. 29, Issue 4, P. 290–298. http://dx.doi.org/10.1016/j.astropartphys.2008.02.006.

21.
MUNU Collaboration, Z. Daraktchieva et. al. Final results on the neutrino
magnetic moment from the munu experiment. Phys. Lett. B615 (2005), 153–159. http://dx.doi.org/10.1016/j.physletb.2005.04.030.

22.
G. G. Raffelt. New bound on neutrino dipole moments from globular
cluster stars, Phys. Rev. Lett. 64 (1990), 2856–2858. http://dx.doi.org/10.1103/PhysRevLett.64.2856.

23.
N. F. Bell, V. Cirigliano, M. J. Ramsey-Musolf, P. Vogel, and M. B.
Wise. How magnetic is the Dirac neutrino? Phys. Rev. Lett. 95 (2005), 151802. http://dx.doi.org/10.1103/PhysRevLett.95.151802.

24.
E.
Williams, J. Faller and H. Hill. New Experimental Test of Coulomb’s Law: A Laboratory
Upper Limit on the Photon Rest Mass. Physical Review Letters, 26 (12),
721 (1971). http://dx.doi.org/10.1103/PhysRevLett.26.721.

25.
Particle
Data Group, Amsler, C. et al. Damour et al. (2008 +2009 partial update). Review
of Particle Physics: Gauge and Higgs bosons. Physics Letters B 667 1-6. http://dx.doi.org/10.1016/j.physletb.2008.07.018.

26.
V. V. Burdyuzha. The fractal universe, preon structure of particles, and
the familon model of dark matter. Astronomy Reports, 2014, Vol. 58, Issue 6, P.
353-362. http://dx.doi.org/10.1134/S106377291406002X.

27.
F. Aharonian et al. (The HEGRA Collaboration). The Crab Nebula and
Pulsar between 500 GeV and 80 TeV: Observations with the HEGRA stereoscopic air
Cherenkov telescopes. The Astrophysical Journal, 614 (2), 897–913 (2004). http://dx.doi.org/10.1086/423931.

Источник: http://sergf.ru/mf.htm

На научный сайт

Источник

Фотон в современной физике считается разновидностью элементарных частиц. В частности, он представляет собой квант электромагнитного излучения (квант — неделимая частица чего-либо).

Энергия и импульс фотона

Фотоны обладают определенной энергией и импульсом. Когда свет испускается или поглощается, он ведет себя подобно не волне, а потоку частиц, имеющих энергию Е = hν, которая зависит от частоты. Оказалось, что порция света по своим свойствам напоминает то, что принято называть частицей. Поэтому свойства света, обнаруживаемые при его излучении и поглощении, стали называть корпускулярными. Сама же световая частица была названа фотоном, или квантом электромагнитного излучения.

Как частица, фотон обладает определенной порцией энергии, которая равна hν. Энергию фотона часто выражают не через частоту v, а через циклическую частоту:ω = 2πν

При этом в формуле для энергии фотона в качестве коэффициента пропорциональности (постоянной Планка) используется другая величина, обозначаемая ℏ и равная:

ℏ=h2π≈1,0545726·10−34 (Дж·с)

Учитывая это, формула для определения энергии фотона примет вид:

Е=ℏω

Согласно теории относительности, энергия частиц связана с массой следующим соотношением:

Е=mс2

Так как энергия фотона равна hν, то, следовательно, его масса m получается равной:

m=hνс2

У фотона нет собственной массы, поскольку он не может существовать в состоянии покоя. Появляясь, он уже имеет скорость света. Поэтому формула выше показывает только массу движущегося фотона.

По известной массе и скорости фотона можно найти его импульс:

p=mc=hνc=hλ

Внимание! Вектор импульса фотона всегда совпадает с направлением распространения луча света.

Чем больше частота ν, тем больше энергия Е и импульс р фотона и тем отчетливее свет проявляет свои корпускулярные свойства. Из-за того что постоянная Планка мала, энергия фотонов видимого излучения крайне незначительна. К примеру, фотоны, свойственные зеленому свету, имеют энергию, равную всего 4∙10^–19Дж. Несмотря на это, человеческий глаз способен различать изменение освещенности, даже если оно измеряется единичными квантами.

Пример №1. Каков импульс фотона, если длина световой волны λ = 5∙10^–7 м?

Корпускулярно-волновой дуализм

Законы теплового излучения и фотоэффекта объясняются только при условии, если начать считать свет потоком частиц. Однако нельзя отрицать тот факт, что свету присущи такие явления как интерференция и дифракция света. Но эти явления встречаются только у волновых процессов. Поэтому в современной физике принято считать свет с дуализмом, иначе — двойственностью свойств.

Когда свет распространяется в средах, он проявляет волновые свойства. Когда он начинает взаимодействовать с веществом (поглощаться или излучаться), проявляются корпускулярные свойства (свойства частицы).

Гипотеза де Бройля

Длительное время электромагнитное поле представлялось как материя, которая распределена в пространстве непрерывно. Электроны же представлялись как очень маленькие частицы материи. Не нет ли здесь ошибки, обратной той, которая была допущена при определении света? Может быть, электрон и другие частицы тоже обладают волновыми свойствами. Такую мысль высказал в 1923 г. французский ученый Луи де Бройль.

Он предположил, что с движением частиц связано распространение некоторых волн. И ученому удалось найти длину волны этих волн. Связь длины волны с импульсом частицы оказалась точно такой же, как и у фотонов. Если длину волны обозначить через λ, а импульс — через р, то получится, что:

λ=hp

Эта формула носит название формулы де Бройля, которая является одной из основных в разделе квантовой физики.

В будущем волновые свойства частиц, о которых предположил де Бройль, были обнаружены экспериментально. Так, удалось получить дифракцию электронов и других частиц на кристаллах. В этих случаях получалась почти такая же картина, как в случае с рентгеновскими и другими лучами. И формула де Бройля также нашла экспериментальное доказательство. Волновые свойства микрочастиц описываются квантовой механикой.

Квантовая механика — раздел физики, изучающий теорию движения микрочастиц.

Внимание! Законы Ньютона в квантовой физике в большинстве случаем не могут быть применены.

Давление света

В 1873 г. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствия. Предсказанное Максвеллом существование светового давления было экспериментально подтверждено Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Оно оказалось чрезвычайно малым, около 4∙10^-7Па.

Световое давление, обусловленное солнечным излучением у поверхности Земли, составляет менее 0,0001 Па. Этим и объясняется тот факт, что в обычных условиях давление света заметным образом себя не проявляет. Но давлением света объясняет следующие факты:

хвосты комет направлены от ядра кометы в сторону, противоположную Солнцу;
изменение орбит искусственных спутников Земли.

Свет — это поток фотонов с импульсом:

p=mc

При поглощении веществом фотон перестает существовать, но импульс его, по закону сохранения импульса, не может исчезнуть бесследно. Он предается телу, значит, на тело действует сила.

Приведенное рассуждение будет абсолютно верным, если считать, что свет только веществом поглощается. Но разве это всегда так, свет еще может отражаться телами, а если тело прозрачно, то может проходить сквозь него. В реальных условиях свет частично отражается телом, частично поглощается, а если это, например, стекло, то свет проходит сквозь него. Как будет обстоять дело, если поверхность зеркальная? Возникает световое давление в данном случае?

Для простоты предположим, что свет падает перпендикулярно к поверхности зеркала. Мы знаем, что при абсолютном ударе какого-либо тела о стенку она получает импульс, модуль которого равен удвоенному модулю импульса тела, то есть 2mv. Отражаясь, фотон летит с той же скоростью, но в противоположном направлении. Значит, при отражении фотона от зеркала его импульс изменяется на 2mc. Такое же изменение импульса, но в противоположном направлении, получит зеркало. Импульс, получаемый телом при отражении фотона, будет в 2 раза больше импульса, получаемого телом при поглощении фотона.

Задание EF17985

За время t=4 с детектор поглощает N=6⋅10⁵ фотонов падающего на него монохроматического света. Поглощаемая мощность P=5⋅10⁻¹⁴ Вт. Какова длина волны падающего света?

Ответ:

а) 0,4 мкм

б) 0,6 мкм

в) 520 нм

г) 780 нм

Алгоритм решения

1.Записать исходные данные.

2.Установить взаимосвязь между энергией фотонов и поглощаемой детектором мощностью.

3.Выполнить решение в общем виде.

4.Подставить известные данные и найти искомую величину.

Решение

Запишем исходные данные:

• Количество фотонов: N = 6∙10⁵ шт.

• Поглощенная мощность: P = 5∙10^–14 Вт.

Вся энергия фотонов будет поглощена детектором. Согласно закону сохранения энергии:

Nhν=Pt

Длина волны определяется формулой:

λ=cν

Отсюда частота равна:

ν=cλ

Подставим это выражение в записанный закон сохранения энергии:

Nhcλ=Pt

Отсюда длина волны равна:

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17986

При изучении давления света проведены два опыта с одним и тем же лазером. В первом опыте свет лазера направляется на пластинку, покрытую сажей, а во втором – на зеркальную пластинку такой же площади. В обоих опытах пластинки находятся на одинаковом расстоянии от лазера и свет падает перпендикулярно поверхности пластинок.

Как изменится сила давления света на пластинку во втором опыте по сравнению с первым? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения.

Алгоритм решения

1.Описать процессы, происходящие во время обоих опытов.

2.С помощью физических формул установить, как изменяется сила давления света.

Решение

В обоих опытах происходит поглощение световой волны. Этот процесс можно рассматривать как поглощение за время t большого числа световых квантов — N >>1 (фотонов). Фотоны поглощаются пластинкой. Причем каждый фотон передает этой пластинке свой импульс, равный:

pф=hνc

Поэтому импульс пластинки становится равным сумме импульсу всех поглощенных фотонов:

pп=Nhνc

В результате поглощения света пластинкой, покрытой сажей, она приобретает за время t импульс pп в направлении распространения света от лазера. Согласно закону изменения импульса, тела в инерциальной системе отсчета скорость изменения импульса тела равна силе, действующей на него со стороны других тел или полей:

F1=pпt=Nthνc

В результате отражения света от зеркальной пластины отраженный фотон имеет импульс, противоположный импульсу фотона падающей волны:

pф=∣∣−pфп∣∣

Поэтому отраженная волна будет иметь импульс:

pов=−N´pф=−N´hνc

N´ — количество отраженных фотонов.

В итоге за время t импульс волны под действием зеркальной пластинки изменился. Это изменение будет равно разности импульса отраженной волны и импульса пластинки:

Δp=pов−pп=−Npф−N´pф=−(N+N´)pф

Согласно закону сохранения импульса, импульс системы, состоящей из световой волны и зеркальной пластинки, сохраняется:

Δ(pп+pпл)=0

Отсюда:

Δpпл=Δpп

Но изменение импульса тела в инерциальной системе отсчета происходит только под действием других тел или полей и характеризуется силой:

F2=pплt=N+N´thνc

Если зеркала отражает хорошо, то N ≈ N´. Тогда:

F2≈2F1

Отсюда видно, что сила давления света увеличится вдвое.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18201

Излучением лазера с длиной волны 3,3⋅10⁻⁷ м за время 1,25⋅10⁴ с был расплавлен лёд массой 1 кг, взятый при температуре 0 °С, и полученная вода была нагрета на 100 °С. Сколько фотонов излучает лазер за 1 с? Считать, что 50% излучения поглощается веществом.

Алгоритм решения

1.Записать исходные данные.

2.Установить, какое количество тепла было сообщено льду для его расплавления и нагревания до температуры кипения.

3.Установить, какая энергия была выделена лазером при условии, что лишь половина этой энергии была сообщена льду.

4.Из полученного выражения выразить количество фотонов, излученных лазером за время t.

5.Записать формулу для количества фотонов, выделяемых за время 1 с.

6.Подставить известные данные и вычислить искомую величину.

Решение

Запишем не только те данные, что есть в условии задачи, но и табличные данные, которые нам понадобятся в ходе решения задачи:

• Удельная теплота плавления льда: λ_льда = 3,4∙10⁵ Дж/кг.

• Удельная теплоемкость воды: c = 4200 Дж/(кг∙^оС).

• Начальная температура льда/воды: t₁ = 0 ^оС.

• Конечная температура воды: t₂ = 100 ^оС.

• Коэффициент полезного действия: η = 50%.

• Длина световой волны: λ_света = 3,3∙10^–7.

• Время проведения всего опыта: t = 1,25∙10⁴.

Чтобы лед расплавился, а образовавшаяся вода нагрелась до температуры кипения, нужно сообщить ему следующее количество энергии:

Q=Q1+Q2=mλльда+mc(t2−t1)

Так как КПД равен 50% (0,5), то это количество теплоты равно половине энергии, выделенной лазером:

Q=ηE

mλльда+mc(t2−t1)=ηE

Энергия, выделенная лазером, равна сумме энергий каждого из излученных фотонов, количество которых будет равно N:

E=Nhν

Но частота световой волны равна:

ν=cλсвета

Тогда:

E=Nhcλсвета

Отсюда:

Nhcλсвета

Теперь мы можем записать:

mλльда+mc(t2−t1)=ηNhcλсвета

Выразим количество излученных фотонов за все время:

N=λсвета(mλльда+mc(t2−t1))ηhc

Если разделить это выражение на время проведения опыта, то мы найдем количество фотонов, излученных за 1 секунду:

N1с=λсвета(mλльда+mc(t2−t1))ηhct

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 2.7k

Источник

Атомная
физика

Квантовая
физика

Методические
рекомендации к решению задач части С

Фотоны.
Постулаты Бора.

№ 1.Монохроматический пучок параллельных лучей создается
источником,
который за время Δt = 8·10^-4 с излучает N = 5·10¹⁴
фотонов.
Фотоны падают по нормали на площадку S = 0,7 см² и создают давление
p = 1,5·10^-5 Па.
При этом 40% фотонов отражается, а 60% поглощается.
Определите длину волны излучения.
Решение:

№
3.
Электромагнитное излучение с длиной волны λ = 3,3·10 ^-7м используется
для нагревания воды массой 1 кг. Сколько времени потребуется для
нагревания воды на Δt^o = 10 ^оС,
если источник за 1 с излучает N = 10²⁰ фотонов? Считать, что излучение полностью поглощается
водой.

Решение. Теплота нагревания воды Q = mc_вΔt ^o, энергия излучения U = hνNt. Излучение полностью поглощается
водой, следовательно, m c_вΔt ^o = hνNt, t = mc_вΔt ^o/hνN. ν = с/ λ.

t = mc_вΔt ^o λ /hсN = 1 · 4200 · 10 · 3,3 · 10^-7/
6,6 · 10 ^-34· 3 ·10⁸·10²⁰ =
4200/6 = 700 (с).

№ 4. На рисунке изображены несколько энергетических уровней
электронной оболочки атома и указаны длины волн фотонов, излучаемых и
поглощаемых при переходах с одного уровня на другой. Чему равна минимальная
длина длина волны фотонов, излучаемых при переходе с одного уровня нр другой,
если λ_1-3 = 400 нм, λ_2-4 = 500 нм, λ_3-2
= 600 нм?

Решение.
Согласно
постулату Бора энергия фотона hν = E₄ – E₁ . Из рисунка видно,
что Е_4-1= Е_2-4 + Е_1-3–
Е_2-3.

hν=hc/ λ. hc/ λ_{4-1 =}hc/ λ_2-4 + hc/ λ_1-3– hc/ λ_2-3.

1/ λ_4-1= 1/ λ_2-4 + 1/ λ_1-3– 1/
λ_2-3 = 1/500 + 1/ 400 – 1/600 = 34/12000, λ_4-1= 352
(нм).

№5.

Реши самостоятельно.

№ 1. Препарат активностью А = 1,7 ·10¹¹
частиц в секунду помещён в медный контейнер массой 0,5
кг. На сколько повысилась температура контейнера за 1 час, если известно, что
данное радиоактивное вещество испускает альфа-частицы энергией Е₁=
5,3 МэВ. Считать, что энергия всех альфа-частиц полностью переходит во
внутреннюю энергию контейнера. Теплоёмкостью препарата и теплообменом с
окружающей средой пренебречь.

№ 2. Образец, содержащий радий, за 1 с
испускает 3,7⋅10¹⁰ α-частиц, обладающих импульсом 1,0⋅10^–19 кг⋅м/с. За какое время выделится энергия 100
Дж? Масса α-частиц равна 6,7⋅10^–27 кг. Энергией отдачи ядер, γ-излучением
и релятивистскими эффектами пренебречь.

№ 3.

На рисунке представлены энергетические уровни

электронной оболочки атома и указаны
частоты

фотонов, излучаемых и поглощаемых при

переходах между этими уровнями. Какова
частота ν₂₄, если ν₁₃= 7·10¹⁴ Гц, ν₃₂
= 3·10¹⁴ Гц, а при переходе с уровня Е₄ на уровень Е₁излучаются фотоны длиной волны λ = 360 нм?

№ 4. На рисунке изображены
энергетические уровни атома и указаны длины волн фотонов, излучаемых и
поглощаемых при переходах с одного уровня на другой. Экспериментально
установлено, что минимальная длина волны для фотонов, излучаемых при
переходах между этими уровнями, равна λ₀ = 250 нм. Какова величина
λ₁₃, если λ₃₂ = 545 нм, λ₂₄ = 400 нм?

№ 5. Мощность излучения лазерной указки с длиной волны 600нм
равна 2мВт. Определите число фотонов, излучаемых указкой за 1с.

№6. Неподвижная
пылинка массой 0,1мг освещается импульсом
лазерного света с длиной волны $lambda = 0,63 cdot 10^{ - 6} ,!$ 0,63мкм. Определите число поглощённых
пылинкой фотонов, если она в результате действия света приобрела скорость 1мм/с.

№7. Электрон,
имеющий импульс p = 2•10^–24
кг•м/с, сталкивается с покоящимся протоном, образуя атом
водорода в состоянии с энергией E_n
(n = 2). В процессе образования атома излучается фотон. Найдите
частоту ν этого фотона, пренебрегая кинетической энергией атома. Уровни энергии
электрона в атоме водорода задаются формулой E_n = -(13.6/n²) эВ,
где n = 1, 2, 3.

№8. Покоящийся
атом излучает фотон с энергией 16,32•10^-19 Дж в
результате перехода электрона из возбуждённого состояния в основное. Атом в
результате отдачи начинает двигаться поступательно в противоположном
направлении с кинетической энергией 8,81•10^-27 Дж.
Найдите массу атома. Скорость атома считать малой по сравнению со скоростью
света.

№ 9. В сосуде находится разреженный атомарный водород. Атом
водорода в основном состоянии (Е₁
= — 13,6 эВ) поглощает фотон с частотой 3,7•10¹⁵ Гц.
С какой скоростью v
движется вдали от ядра электрон, вылетевший из атома в результате ионизации?
Энергией теплового движения атомов водорода пренебречь.

№ 10.В сосуде находится разреженный атомарный водород. Атом
водорода в основном состоянии (Е₁
= — 13,6 эВ) поглощает фотон с частотой 3,7•10¹⁵ Гц.
С какой скоростью v
движется вдали от ядра электрон, вылетевший из атома в результате ионизации?
Энергией теплового движения атомов водорода пренебречь

Уравнение Эйнштейна для
фотоэффекта.

№ 1. В вакууме
находятся два покрытых кальцием электрода, к которым подключен конденсатор
ёмкостью С. При длительном освещении катода светом с длиной волны λ=100нм
фототок, возникший вначале, прекращается, а на конденсаторе появляется заряд q
= 9,6•10^-10 Кл. Работа выхода электрона из кальция А=4,42•10^-19
Дж. Определите ёмкость конденсатора С.

Решение.
Напряжение на конденсаторе U будет равно задерживающей разности потенциалов U_з,
которое можно найти из уравнения Эйнштейна для фотоэффекта: hν = A_вых+Е_к, Е_к=еU_з, V=c/λ, т.е. v=3 ·10⁸/10^-7=3·10¹⁵Гц.
Тогда
, Отсюда:

1/1,6·10^-19(6,63·10^—34·3·1015-4,42·10^-19)=9,6В.

Находим емкость конденсатора:

9,6•10^-10/9,6=10^-10Ф.

№ 2. Уровни энергии электрона в
атоме водорода задаются формулой

эВ, где n = 1, 2, 3,
…

При переходе из состояния Е₂ в состояние Е₁ атом
испускает фотон.
Поток таких фотонов падает на поверхность фотокатода.
Запирающее напряжение для фотоэлектронов, вылетающих с поверхности фотокатода U_зап
= 7,4 В.
Какова работа выхода А_вых фотоэлектронов с поверхности фотокатода?

Решение.

Энергия фотона:
hν = E₂ — E₁ .
Уравнение Эйнштейна для фотоэффекта: hν = A_вых —
eU_зап.

Е₁=-13,6/1²=-13,6эВ,
Е₂=-13,6/2²=-3,4эВ, Е₂-Е₁=-10,2эВ=-16,32·10^-19Дж.

Отсюда
A_вых =(E₂ — E₁) —
eU_зап , А_вых= -16,32·10^-19Дж+1,6·10^-19·7,4=4,54,5·10^–19
Дж

Ответ: А_вых ≈ 4,5·10^–19 Дж ≈ 2,8
эВ.

№3.
Уровни энергии электрона в
атоме водорода задаются формулой

, где n = 1, 2, 3, … . При переходе
атома из состояния Е₂в
состояние Е₁ атом испускает фотон. Попав на поверхность
фотокатода,                                         фотон выбивает
фотоэлектрон. Длина волны света, соответствующая                                         красной
границе фотоэффекта для материала поверхности
фотокатода,                                                 λкр = 300 нм. Чему максимальная возможная скорость
фотоэлектронов?

Решение:

№5.

Решение.

Реши самостоятельно
№ 1. В сосуде находится разрежённый атомарный
водород. Атом водорода в основном состоянии (Е₁ = – 13,6 эВ)
поглощает фотон и ионизуется. Электрон, вылетевший из атома в результате
ионизации, движется вдали от ядра со скоростью 1000 км/с. Какова
частота поглощённого фотона? Энергией теплового движения атомов водорода
пренебречь.

№
2.
В
двух опытах по фотоэффекту металлическая пластинка облучалась светом с длинами
волн соответственно λ₁=350 нм. и λ₂=540 нм.
Максимальные скорости фотоэлектронов в первом и во втором опытах отличались в 2
раза. Какова работа выхода с поверхности металла?

№
3. Для увеличения яркости изображения слабых источников
света используется вакуумный прибор – электронно-оптический преобразователь. В
этом приборе фотоны, падающие на катод, выбивают из него фотоэлектроны, которые
ускоряются разностью потенциалов U = 15000 В и бомбардируют
флюоресцирующий экран, рождающий вспышку света при попадании каждого электрона.
Длина волны падающего на катод света λ₁=820 нм, а
света, излучаемого экраном, λ₂= 410 нм. Во
сколько раз N прибор увеличивает число фотонов, если 1
фотоэлектрон рождается при попадании на катод в среднем k = 10 фотонов?
Работу выхода электронов принять равной 1эВ. Считать, что энергия
падающих на экран электронов переходит в энергию света без потерь.

№
4. Уровни энергии электрона в атоме водорода задаются
формулой E_n = -13,6/n² эВ, где n =1, 2, 3, … . При переходе
атома из состояния E₂ в состояние E₁, атом испускает
электрон. Попав на поверхность фотокатода, фотон выбивает фотоэлектрон. Длина
волны света, соответствующая красной границе фотоэффекта для материала
поверхности фотокатода равна 300 нм. Чему равна максимальная возможная
скорость фотоэлектронов?

№
5.
Фотокатод облучают светом длиной волны λ₁=
300нм. Красная граница фотоэффекта для вещества фотокатода λ₂= 450 нм. Какое напряжение между анодом и катодом нужно создать,
чтобы фототок прекратился?

№6.Уровни энергии
электрона в атоме водорода задаются формулой

, где n = 1, 2, 3, … . При переходе
атома из состояния Е₂в                                        состояние
Е₁ атом испускает фотон. Попав на поверхность фотокатода,
фотон выбивает фотоэлектрон. Длина волны света, соответствующая                                               красной
границе фотоэффекта для материала поверхности фотокатода,
λкр = 300 нм. Чему максимальная возможная скорость
фотоэлектронов?

№ 7.Какова максимальная скорость электронов, выбиваемых из металлической пластины светом с длиной волны λ = 3•10^-7 м, если красная граница фотоэффекта λ_кр = 540 нм?
№8. Фотоны, имеющие энергию 5 эВ, выбивают электроны с поверхности металла. Работа выхода электронов из металла равна 4,7 эВ. Какой импульс приобретает электрон при вылете с поверхности металла?
№ 9. В вакууме находятся два покрытых кальцием электрода, к которым подключен конденсатор емкостью С = 8000 пФ. При длительном освещении катода светом c частотой ν = 10¹⁵ Гц фототок, возникший вначале, прекращается. Работа выхода электронов из кальция А = 4,42•10^-19 Дж. Какой заряд q при этом оказывается на обкладках конденсатора?
№ 10. Фотокатод, покрытый кальцием (работа выхода 4,42•10^-19 Дж), освещается светом с длиной волны 300 нм. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией 8,3•10^-4 Тл перпендикулярно линиям индукции этого поля. Каков максимальный радиус окружности, по которой движутся электроны

Закон радиоактивного распада.

№ 2.Активность препарата ³²P равна 2 мкКи.
Сколько весит такой препарат?
Решение.

Закон радиоактивного распада: N(t) = N₀e^-λt,где N₀
— количество радиоактивных ядер в произвольно выбранный начальный момент
времени t = 0, N(t) — количество радиоактивных ядер, не распавшихся к
моменту времени t, λ — постоянная распада (вероятность распада в единицу
времени). λN — активность (интенсивность излучения) радиоактивного препарата,
измеряется в Ки, 1 Ки = 3.7·10¹⁰ распадов/с. T_1/2
— период полураспада данного ядра (время, в течение которого количество
радиоактивных ядер уменьшается в два раза) равен для ³²P
14.5 суток. Период полураспада T_1/2 связан с постоянной распада
λ соотношением T_1/2 = ln 2/λ.
Количество ядер в образце массой m грамм

где N_A — число Авогадро, A — массовое число. Активность
препарата

тогда его масса будет

7.1·10^-12 г.

№ 3.
Определить период полураспада радиоактивного изотопа, если 5/8 начального
количества ядер этого изотопа распалась за время t = 849 c.

Решение.

Используя
закон радиоактивного распада , найдем

Прологарифмировав
последнее выражение , найдем .
Тогда период полураспада

мин.

№ 4. Природный уран состоит на из
изотопа U
и на —
из .
По современным представлениям, все элементы тяжелее железа образовались при
взрывах сверхновых звёзд, а после этого из получившихся газопылевых облаков
возникли звёзды следующего «поколения», в частности, Солнце и планеты Солнечной
системы. По-видимому, в этих выбросах всех изотопов урана было примерно
поровну. Оцените, сколько лет назад произошёл тот выброс вещества, из которого
сформировалась наша Земля. Период полураспада, то есть время, в течение
которого число атомов данного изотопа уменьшается в 2 раза, для равно
лет,
а для —
лет.

Решение                                                                                                                                                Обозначим
количество атомов каждого изотопа непосредственно после взрыва сверхновой звезды
через N₀. Тогда
через время T₁ после
взрыва количество атомов стало
равно N₀/2, через
время 2Т₁ — стало равно N₀/2²
,
и так далее. Очевидно, что через время t=nT₁ после
взрыва, равное периодам
полураспада ,
количество атомов этого изотопа стало равно N₁=N₀/2ⁿ .                                                                                                        Аналогично,
за то же самое время t=rT₂, равное периодам
полураспада ,
количество атомов данного изотопа стало равно N₂=N₀/2^k .
По условию задачи, $begin{displaymath} n_{1} = mathchoice{displaystylefrac{N_1}{N_1+N_2}}{disp... ...ystylefrac{N_2}{N_1+N_2}}{displaystylefrac{N_2}{N_1+N_2}}. end{displaymath}$       Отсюда
$begin{displaymath} mathchoice{displaystylefrac{n_2}{n_1}}{displaystylefra... ...tylefrac{2^n}{2^k}}{displaystylefrac{2^n}{2^k}} = 2^{n-k}. end{displaymath}$

Учитывая, что t=nT₁+kT₂ ,
получаем систему из двух уравнений относительно неизвестных и
.
Решая её, найдём, например, :

$begin{displaymath} k = mathchoice{displaystylefrac{lg(n_2/n_1)}{lg 2}}{d... ...ystylefrac{T_1}{T_2-T_1}}{displaystylefrac{T_1}{T_2-T_1}}. end{displaymath}$

Значит, искомое
время равно
$begin{displaymath} t = kT_{2} = mathchoice{displaystylefrac{lg (n_2/n_1)}... ...frac{T_1 T_2}{T_2-T_1}} approx 6 cdot 10^{9} mbox{лет}. end{displaymath}$

№ 5. Конечным продуктом радиоактивного распада
является свинец Период полураспада составляет 4,5•109 лет. Определите возраст
минерала, в котором число атомов урана и свинца одинаково.

Дано:

Решение:

По закону
убывания числа радиоактивных атомов со временем:

значит,

Реши
самостоятельно

№1. . Радиоактивный фосфор, использующийся для диагностики
болезней кровообращения, имеет период полураспада 14,3 дня. Найдите активность
образца с числом атомов N = 5 • 1016.

№.2. Определить какая часть начального количества начального
количества ядер радиоактивного изотопа распадется за время t, равное
двум периодам полураспада.

№ 3 .Образец радиоактивного радия находится в
закрытом сосуде. Ядра радия испытывают распад с
периодом полураспада 11,4 суток. Определите число атомов радия, которые
останутся нераспавшимися через 34,2 суток, если образец в момент помещения его
в сосуд содержал атомов радия.

№4.Имеется 8 кг
радиоактивного цезия. Определите массу нераспавшегося цезия после 135 лет
распада, если период полураспада 27 лет. (m= 0,25
кг).

№ 5.Имелось некоторое
количество радиоактивного серебра. Масса серебра уменьшилась в 8 раз за 810
суток. Определите период полураспада. (Т= 270 суток).

№ 6.
Сколько процентов ядер радиоактивного йода–131 с периодом
полураспада 8 суток останется 16 сут?

Элементарные частицы.

Задача
1.

Ядро покоящегося нейтрального атома, находясь в однородном
магнитном поле индукцией В, испытывает α-распад.
При этом рождается α-частица и тяжёлый ион нового элемента. Трек
тяжёлого иона находится в плоскости, перпендикулярной направлению магнитного
поля. Начальная часть трека напоминает дугу окружности радиусом
.Выделившаяся при α-распаде энергия ΔЕ целиком
переходит в кинетическую энергию продуктов распада. Масса α-частицы
равна m_a, её заряд 2е.
Найти модуль отношения заряда к массе │q/М│ для тяжёлого иона.

Решение.
1. На
основании закона сохранения зарядов модули зарядов продуктов распада будут
равны q_и = q_а = q.

2.
Так как нейтральный атом в начале покоился, то его импульс равен нулю,
следовательно, и суммарный импульс продуктов распада тоже равен нулю (основание
– закон сохранения импульса). Отсюда следует, что модули импульсов продуктов
распада будут равными. m_aυ_a= M υ_и.

3.
Ион под действием силы Лоренца начинает двигаться по дуге радиусом R. Сила Лоренца сообщает иону
центростремительное ускорение: q_иBυ =Mυ²/R, q_и BR = M υ_и.

4. А
также по условию имеем ΔЕ = Е_а + Е_и , 2 ΔЕ = m_aυ_a²+ M υ_и²

Решая
систему уравнений (выделены красным), получим: υ_a = M υ_и/m_a, υ_и = q_и BR/ M, υ_a = q_и BR/m_a_. Подставляя значение
скоростей продуктов распада в 4-е уравнение, получим
2 ΔЕ = m_a(q_и BR/m_a)²+ M(q_и BR/ M) ²,

2 ΔЕ = q²B²R²/m_a+
q²B²R²/ M, q/ M = (2 ΔЕ — q²B²R²/m_a)
/ qB²R². Умножив числитель и знаменатель на q и, выполнив ряд алгебраических
преобразований, получим q/ M =(q/m_а) ( (2 ΔЕ m_а / q²B²R²) -1) ,

q/ M =(2е/m_а) ( (2 ΔЕ m_а / 4е²B²R²)
-1)

№ 3. Свободный пион (π⁰-мезон) с энергией
покоя 135 МэВ движется со скоростью V, которая значительно меньше
скорости света.
В результате его распада образовались два γ-кванта, причём один из
них распространяется в направлении движения пиона, а другой – в
противоположном направлении.
Энергия одного кванта на 10% больше, чем другого.
Чему равна скорость пиона до распада?

Решение.

Пион, движущийся со скоростью V, имеет импульс p = mV и энергию , где m – масса пиона.

Энергия γ-кванта E_γ и его импульс р_γ
связаны соотношением:

При распаде пиона на два кванта энергия системы и её импульс сохраняются:
Разделив второе уравнение на первое, получим: .

По условию задачи E₁ =1,1⋅ E₂ , так что

Ответ: V ≈1,43⋅10⁷ м/с .

Реши самостоятельно

№1.π₀-мезон массой 2,4•10^-28
кг распадается на два γ-кванта. Найдите модуль импульса одного из
образовавшихся γ-квантов в системе отсчета, где первичный π₀-мезон
покоится.

№ 2. Атом мюония состоит из
неподвижного протона и отрицательно заряженного мюона массой m = 206m_e,
где m_e — масса электрона, и зарядом, равным заряду
электрона e. Для ближайшей к протону орбиты мюона выполняется условие
квантования 2π rp = h, где r — радиус орбиты, р —
импульс мюона, h — постоянная Планка. Найдите радиус этой орбиты.

№.3. Рассматриваемая
реакция идёт с поглощением энергии 1,3 МэВ. При какой пороговой
(минимальной) скорости α-частиц,
бомбардирующих неподвижную мишень, такая реакция могла пойти? Масса α-частицы $m_{He} = 6,6 cdot 10^{ - 27} ,!$ 6,6·10 ^-27кг.

Ядерные реакции.

№1. Вычислите энергию связи ядра атома
дейтерия.

Дано:

____________________

Решение:

Энергия связи ядра равна

где Δm – разность суммы масс
свободных частиц, входящих в состав ядра, и массы ядра, с – скорость
света в вакууме. Для нахождения разности масс отыскиваем в справочнике по
физике сведения о массах протона ,
нейтрона , электрона
и атома дейтерия .
Для нахождения массы ядра дейтерия необходимо
вычесть из массы атома дейтерия массу электрона, находящегося на его
оболочке:

Но ,
поэтому

№ 2. Вычислите энергетический выход
ядерной реакции

Решение:

Для вычисления энергетического выхода ядерной реакции необходимо
найти разность масс частиц, вступающих в реакцию, и частиц – продуктов реакции.
В реакции участвуют атомные ядра, но в справочных таблицах обычно даются
сведения лишь о массах атомов. Можно найти массу каждого атомного ядра
вычитанием массы электронов оболочки из массы атома. Можно поступить иначе.
Если в уравнении ядерной реакции слева и справа пользоваться только массами
атомов (т.е. массой атома водорода, а не массой протона слева, и массой атома
гелия, а не массой альфа-частицы справа), то из-за одинаковости числа
электронов в атомах, вступающих в реакцию, и в продуктах реакции их вычитание
осуществляется автоматически при нахождении разности масс. Таким образом, для
решения задачи можно воспользоваться сведениями из справочника о массах атомов.

_____________________

Вычислим энергетический выход
при изменении массы на 1 а.е.м.:

Выход ядерной реакции равен

Реши самостоятельно.

№ 1.Найти с помощью табличных значений масс атомов:
а) среднюю энергию связи на один нуклон в ядре О¹⁶;
б) энергию связи нейтрона и α-частицы в ядре B¹¹;
в) энергию, необходимую для разделения ядра O¹⁶ на четыре одинаковые
частицы.

№2. Неподвижное ядро
франция Fr с массовым числом А = 221 претерпевает альфа-распад.
Определите энергетический выход данной реакции, если кинетическая энергия
образовавшегося ядра астата At равна Е_At = 0,1184
МэВ, а его атомный номер Z = 85. При расчетах учесть движение
образовавшихся ядер и считать, что скорости частиц много меньше скорости
света.

№3. При реакции синтеза образуется
ядро изотопа гелия и нейтрон и выделяется энергия Е = 3,27 МэВ. Какую
кинетическую энергию уносит ядро изотопа гелия, если суммарный импульс
исходных частиц равен нулю, а их кинетическая энергия пренебрежимо мала по
сравнению с выделившейся?

№4. Ядро покоящегося нейтрального атома,
находясь в однородном магнитном поле индукцией В, испытывает α-распад.
При этом рождаются α-частица и тяжелый ион нового элемента. Масса α-частицы
равна m_α, ее заряд равен 2e, масса тяжелого иона равна
M. Выделившаяся при α-распаде энергия ΔE целиком переходит в
кинетическую энергию продуктов реакции. Трек тяжелого иона находится в
плоскости, перпендикулярной направлению магнитного поля. Начальная часть этого
река напоминает дугу окружности. Найдите радиус этой окружности.

Комбинированные
задачи.

№ 1. Металлическая пластина облучается
светом с частотой 1,6·10¹⁵Гц. Работа выхода из данного металла равна
3,7эВ. Вылетающие из пластины электроны попадают в однородное электрическое
поле напряжённостью 130В/м. Вектор напряжённости направлен перпендикулярно
поверхности пластины. Какова максимальная энергия фотоэлектронов на
расстоянии 10см от пластины?

Решение.
Электрическое поле совершает работу по перемещению электрона А=qU.
Работа поля, с другой стороны, равна изменению кинетической энергии
электрона    А=Е_к2-Е_к1.                                                                                                                                                     Получаем
Е_к2-Е_к1= qU. Тогда Е_к2= Е_к1=+qU.
Из уравнения Эйнштейна для фотоэффекта hv=А_вых+Е_к1 получаем, что Е_к1= hv-А_вых.Окончательно
Е_к2= hv-А_вых+ qU., где U=Ed.                                                                                                  Подставив
данные, получаем Е_к2= 4,8·10^-19Дж.

№2. Электроны, вылетевшие в
положительном направлении оси Ох под действием света с катода фотоэлемента,
попадают в электрическое и магнитное поля. Какой будет работа выхода с
поверхности фотокатода, чтобы в момент попадания самых быстрых электронов в
область полей, действующих на них, сила была направлена вдоль оси Оу в
положительном направлении? Частота света 6,5·10¹⁴Гц, напряжённость
электрического поля 300В/м, индукция магнитного поля 1мТл.

Решение.                                                                                                                                                  hv=А_вых+Е_к .
                                                                      По
правилу левой руки находим, что сила Лоренца направлена влево и равна F_Л=qBv, сила Кулона направлена вправо и равна F_к=qE.                                                                                                       Приравняв
правые части формул и выразив скорость, получим, что v=Е/В.    Из уравнения Эйнштейна   А_вых=
hv-Е_к., где Е_к=mv/2.
Подставив
числовые значения, получим, А_вых=2·10^-20Дж.

Реши самостоятельно.

№ 1. Фотоэлектроны, выбитые рассеянным светом частоты 6,7·10¹⁴Гц
из металла с работой выхода 1,89эВ, попадают в однородное электрическое
поле. Какова напряжённость поля, если длина тормозного пути у фотоэлектронов,
чья начальная скорость максимальна и направлена вдоль силовых линий
электрического поля, составляет 8,75мм?

№2. Фотокатод,
покрытый кальцием ( Ав=4,42·10^-19 Дж), освещается светом, у которого
длина волны 300 нм. Вылетевшие из катода электроны попадают в однородное
магнитное поле индукцией 8,3·10^-4 Тл перпендикулярно линиям индукции
этого поля. Чему равен максимальный радиус окружности, по которой движутся
электроны? Ответ выразить в мм.

№ 3. Фотокатод (работа выхода А = 4,42*10^-19Дж) освещается
светом с частотой ν. Вылетевшие из катода электроны попадают в однородное
магнитное поле индукцией В=4*10^-4 Тл перпендикулярно линиям индукции
и движутся по окружности, у которой максимальный радиус R=10мм. Чему равна
частота падающего света?

Источник

В этой статье мы собираемся обдумать взаимосвязь энергии и длины волны вместе с примерами и решить некоторые задачи, чтобы проиллюстрировать то же самое.

Энергия находится в прямой зависимости от частоты электромагнитных излучений. Если длина волны увеличивается, это означает, что повторяемость волны будет уменьшаться, что непосредственно влияет на энергию частицы в волне.

Формула соотношения энергии и длины волны

Энергия частицы может быть связана с ее скоростью во время распространения. Скорость частицы дает представление о частоте и длине волны. Если длина волны мала, то частота и, следовательно, энергия частицы будут увеличиваться.

Если колебания частицы больше в траектории пути, то возвратность частицы в волну больше и длина волны мала, это означает, что энергия, которой обладает частица, больше.

Энергия любого тела связана с его длиной волны уравнением

E=hc/λ

Где «h» — постоянная Планка h = 6.626 * 10^-34Js

C — скорость света c=3 *10⁸ м/с и

λ — длина волны света

Энергия обратно пропорциональна длине волны света. Чем меньше длина волны, тем больше энергия частицы в волне.

Задача 1: Рассчитать энергию фотонов, испускающих красный свет. Считайте длину волны луча красного света равной 698 нм. Какова будет энергия, если длина волны уменьшится до 500 нм, то есть если источник излучает зеленый свет?

Данный:λ₁=698нм

λ₂=500 нм

ч = 6.626 * 10^-34 Js

с=3 * 10⁸ м/с

У нас есть,

E=hc/λ₁

E = 6.626 * 10^-34 Дж* 3 * 10⁸ м/с/698* 10^-9m

=0.028* 10^-17=28* 10^-20Дж

Энергия красной длины волны 28* 10^-20Джоули.

Если длина волны λ₂=500 нм

Тогда энергия, связанная с зеленым светом, равна

E=hc/λ₂

E = 6.626 * 10^-34 Дж* 3 * 10⁸ м/с / 500* 10^-9m

= 0.03910^-17=39* 10^-20Дж

Мы видим, что энергия увеличилась до 39*10^-20Джоулей при уменьшении длины волны.

Подробнее о Влияние преломления на длину волны: как, почему, подробные факты.

График взаимосвязи энергии и длины волны

По мере увеличения длины волны частота волны падает, тем самым уменьшая энергию, которой обладает волна. Если мы построим график зависимости энергии от длины волны появляющейся частицы, то график будет выглядеть так, как показано ниже.

График зависимости энергии от длины волны

Приведенный выше график ясно показывает, что по мере увеличения длины волны энергия, связанная с частицей, уменьшается экспоненциально.

Связь кинетической энергии и длины волны

Если скорость частицы больше, то очевидно, что кинетическая энергия частицы велика. Кинетическая энергия определяется уравнением

КЭ=1/2мВ²

Где m — масса объекта или частицы

V — скорость массы

Мы можем записать приведенное выше уравнение как

2E=мв²

Умножение «m» в обеих частях уравнения

2mE=(мВ)²

Импульс объекта определяется как произведение массы объекта на скорость, с которой он движется.

p = mv

Следовательно, приведенное выше уравнение становится

P²=2 мВ

P=√2mE

Согласно де Бройлю,

λ =h/p

Подставляя приведенное выше уравнение, мы имеем

λ =h/ √2mE

Приведенное выше уравнение дает связь между энергией и длиной волны частицы.

Подробнее о Что такое кинетическая энергия света: подробные факты.

Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10^-31кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.

Данный: λ = 293 нм

м = 9.1 × 10^-31kg

ч = 6.626 * 10^-34Js

с=3 *10⁸ м/с

У нас есть,

λ =h/ √2mE

λ²=h²/ 2мЕ

Е = ч²/ 2мλ²

=(6.626 * 10^-34 Дж)²/2* 9.1* 10^-31* (293*10^-9) ²

= 0.28 * 10^-23

Кинетическая энергия, связанная с частицей, равна 0.28*10^-23 Джоули.

Теперь, чтобы вычислить скорость частицы, выведем формулу скорости из кинетической энергии:

КЕ=1/2 мВ²

2E= мв²

v=√(2Е/м)

= √(2(0.28*10^-23)/(9.8*10^-31))

= 0.24 * 10⁴= 2400 м / с

Скорость частицы с длиной волны 298 нм составляет 2400 м/с.

Связь энергии электрона и длины волны

Энергия электрона определяется простым уравнением:

Е=чню

Где «h» — постоянная Планка, а

nu — частота появления электрона

Частота электрона определяется как

ню = v / λ

Где v — скорость электрона и

λ — длина волны электронной волны

Следовательно, энергия связана с длиной волны электрона как

E=hv/λ

Это соотношение позволяет найти энергию, связанную с распространением одиночного электрона с определенной длиной волны, скоростью и частотой. Энергия обратно пропорциональна длине волны. Если длина волны электрона уменьшается, энергия волны должна быть больше.

Электромагнитные волны;
Изображение Фото: Pixabay

Получив энергию в той или иной форме, электрон переходит из более низкого энергетического состояния в более высокое энергетическое состояние. Для перехода электронов из одного состояния в другое энергия электрона определяется уравнением

Э=Р_E(1/н_f– 1/н_i)

Где R_E=-2.18* 10^-18m^-1 является константой Ридберга

n_f это конечное состояние электрона

n_i это начальное состояние электрона

Мы можем далее переписать приведенное выше уравнение как

ч ню = R_E(1/н_f– 1/н_i)

hc/λ =R_E(1/н_f– 1/н_i)

1/λ =R_Ehc(1/n_f– 1/н_i)

1/λ =R(1/n_f– 1/н_i)

Где,

Р=Р_Eчс=1.097* 10⁷

По мере того, как электрон получает энергию, электрон переходит и перескакивает в более высокое состояние энергетического уровня и высвобождает энергию электронам, присутствующим в этом состоянии, и либо становится стабильным, либо высвобождает количество энергии и возвращается в более низкие энергетические состояния.

Подробнее о 16+ Пример амплитуды волны: подробные пояснения.

Задача 3: Если электрон переходит из состояния n_i=1, чтобы указать n_f=2, затем рассчитайте длину волны электрона.

Данный:

n_i=1

n_f=2

1/λ =R_E(1/н_f– 1/н_i)

1/λ=-1.097*10⁷ * ( 1/2-1/1 )

1/λ=0.5485* 10⁷

Следовательно,

λ = 1/0.5485* 10⁷

λ =1.823*10^-7

λ =182.3*10^-9=182.3нм

Длина волны света, излучаемого при переходе электрона с одного энергетического уровня на другой, равна 182.3 нм.

Связь лучистой энергии и длины волны

Каждый объект поглощает световые лучи в дневное время в зависимости от его формы, размера и состава. Если температура поверхности объекта достигает температуры выше абсолютного нуля, объект будет излучать излучения в виде волн.

Это испускаемое излучение пропорционально четвертой степени абсолютной температуры объекта и определяется уравнением

U=ɛΣ Т^4A

Где U — излучаемая энергия

ɛ — коэффициент излучения излучения от объекта

Σ — постоянная Стефана-Больцмана, равная Σ=5.67*10^-8Вт / м²K⁴

T — абсолютная температура

А — площадь объекта

Объект с высокой температурой излучает излучение с короткими длинами волн, а более холодные поверхности излучают волны с большей длиной волны. В зависимости от испускаемого излучения и длины волны испускаемого излучения волны классифицируются в соответствии с приведенной ниже таблицей.

Имя и фамилия	Радиоволны	Микроволны	Инфракрасный порт	Видимый	Ультрафиолетовое	рентген	Гамма излучение
Длина волны	> 1м	1mm-1m	700нм-1мм	400nm-700nm	10nm-380nm	0.01nm-10nm	<0.01 нм
частота	<300 МГц	300MHz-300GHz	300ГГц-430ТГц	430ТГц-750ТГц	750ТГц-30ФГц	30PHz-30EHz	>30 Гц

По мере уменьшения длины волны излучения частота волны возрастает. Длина волны напрямую связана с температурой, поэтому, если частота испускаемого излучения больше, это означает, что энергия объекта высока.

Гамма-лучи, рентгеновские лучи и ультрафиолетовые лучи имеют очень короткую длину волны, поэтому энергия этих волн очень высока по сравнению с видимым, инфракрасным, микроволнами или радиоволнами. Кроме того, чем выше излучение, полученное объектом, тем больше он будет излучать в зависимости от коэффициента излучения объекта.

Ниже приведен график зависимости энергии от длины волны в секунду для разных температур. График показывает, что по мере повышения температуры системы энергия испускаемого излучения также увеличивается с температурой.

График зависимости энергии от длины волны излучения излучения

Для длины волны в видимой области эмиссия излучения максимальна. Это связано с тем, что Солнце излучает УФ-лучи вместе с инфракрасными лучами и видимыми лучами, а эти лучи представляют собой электромагнитные волны дальнего действия. Озоновый слой Земли защищает земную атмосферу от этого вредного излучения и либо отражается обратно, либо задерживается в облаках.

В видимом диапазоне в дневное время излучается больше излучений, поскольку в дневное время от Солнца поступает все больше и больше излучений, а испускается меньше ИК-лучей по сравнению с видимым спектром. Ночью температура снижается, длина волны излучения увеличивается, и объект излучает больше ИК-лучей.

Подробнее о Свойства преломления: волна, физические свойства, исчерпывающие факты.

Задача 4: Коробка длиной 11 см, шириной 2 см и воздухом 7 см нагревается до температуры 1200 Кельвинов. Если коэффициент излучения ящика равен 0.5, то рассчитайте скорость излучения энергии из ящика.

Данный:л=11см

ч=2см

б = 7cm

е =0.5

Σ=5.67* 10^-8Вт / м²K⁴

Т=1200 К

Общая площадь ящика составляет

A=2(фунт+чб+гл)

=2(11*7+7*s 2+2*11)

=2 (77+14+22)

=0.0226 кв.м

Энергия, излучаемая коробкой, равна

U=ɛ Σ T^4A

=0.5* 5.67* 10^-8* 1200⁴* 0.0226

=1328.6 Вт

Связь частоты энергии и длины волны

Чем больше частота волны, тем больше энергия, связанная с частицей. Энергия связана с частотой волны как

E=ч/ню

Где «h» — постоянная Планка.

nu — частота волны

Частота волны определяется как скорость волны в среде и длина волны.

ню = v / λ

Где v — скорость волны

λ — длина волны

Следовательно,

λ=v/ну

Это дает связь между частотой и длиной волны волны. Это говорит о том, что длина волны и частота обратно пропорциональны друг другу. Если длина волны увеличивается, частота волны уменьшится.

Подробнее о Влияние преломления на частоту: как, почему нет, подробные факты.

Задача 5. Скорость луча света, испускаемого источником, равна 1.9 × 10⁸РС. Частота возникновения излучаемой волны составляет 450ТГц. Найдите длину волны испускаемого излучения.

Данный: v=1.9*10⁸ м/с

F=450ТГц=450*10¹²Hz

Длина волны луча света равна

λ = v/f

=1.9* 10⁸/ 450* 10¹²

= 0.004222 * 10^-4

=422.2* 10^-9=422.2нм

Луч света имеет длину волны 422.2 нм.

Связь энергии фотона и длины волны

Энергия, которой обладает фотон, называется энергией фотона и обратно пропорциональна электромагнитной волне фотона по соотношению

E=hc/λ

Где «h» — постоянная Планка.

С — скорость света

λ — длина волны фотона

Частота фотона определяется уравнением

f=с/λ

Где f — частота

Следовательно, фотон с большей длиной волны обладает небольшой единицей энергии, тогда как фотон с меньшей длиной волны дает большое количество энергии.

Подробнее о Какова длина волны фотона: как найти, несколько идей и фактов.

Задача 6: Рассчитать энергию фотона, распространяющегося в электромагнитной волне с длиной волны 620 нм.

Данный: Длина волныλ =620 нм

ч = 6.626 * 10^-34 js

с=3 *10⁸ м/с

У нас есть,

E=hc/λ

Е=6.626 * 10^-34 Дж*3 * 10⁸м/с/620* 10^-9m

= 0.032 * 10^-17= 32 * 10^-20Дж

Энергия, связанная с фотоном, равна 32* 10^-20Джоули.

Часто задаваемые вопросы

Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 10⁶м/с

Данный: v=6.35*10⁶м/с

м=9.1*10^-31kg

ч=6.62* 10^-34Js

Кинетическая энергия электрона равна

КЕ=1/2 мВ²

=1/2 * 9.1*10^-31* (6.35* 10⁶)²

=1.83* 10^-17Дж

Импульс электрона равен

P=√2mE

=√2* 9.1* 10^-31* 1.83 * 10^-17

= 5.7 * 10^-24кг.м / с

Теперь длина волны электрона

λ =h/√2mE

= 6.62 * 10^-34/ 5.7 * 10^-24

= 4.8 * 10^-10m

=48нм

Длина волны электрона, движущегося со скоростью 6.35*10⁶м/с составляет 48 нм.

Q2. Черный объект площадью 180 кв.м находится при температуре 550К. Какова скорость излучения энергии от объекта?

Данный: А=180 кв.м

Т=550К

Поскольку объект имеет черный цвет, коэффициент излучения равен 1.

е =1

У нас есть,

U=ɛΣT^4A

=1*с 5.67* 10^-8* 550⁴* 180

= 0.93 * 10⁶МОЩНОСТЬ

Мощность излучения от выброса излучения от объекта составляет 0.93*10⁶Вт.

Какова абсолютная температура системы?

Это неизменное и совершенное значение температуры системы.

Абсолютная температура системы измеряется по шкале градусов Цельсия, Фаренгейта или Кельвина, которые измеряют ноль как абсолютный ноль градусов.

Как длина волны фотона зависит от температуры?

Температура системы определяет подвижность частиц системы.

Чем больше излучений получает система при более высоких температурах, тем больше излучения будет излучаться системой. При более высоких температурах излучаются более короткие волны, а при более низких температурах излучаются более длинные волны.

Источник

Атом Бора.

Постулаты Бора.

Атом водорода.

Достоинства и недостатки теории Бора.

Энергия и импульс фотона

Корпускулярно-волновой дуализм

Гипотеза де Бройля

Давление света

Формула соотношения энергии и длины волны

График взаимосвязи энергии и длины волны

Связь кинетической энергии и длины волны

Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10-31 кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.

Связь энергии электрона и длины волны

Задача 3: Если электрон переходит из состояния ni=1, чтобы указать nf=2, затем рассчитайте длину волны электрона.

Связь лучистой энергии и длины волны

Связь частоты энергии и длины волны

Связь энергии фотона и длины волны

Задача 6: Рассчитать энергию фотона, распространяющегося в электромагнитной волне с длиной волны 620 нм.

Часто задаваемые вопросы

Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 106 м/с

Q2. Черный объект площадью 180 кв.м находится при температуре 550К. Какова скорость излучения энергии от объекта?

Какова абсолютная температура системы?

Как длина волны фотона зависит от температуры?

Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10^-31кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.

Задача 3: Если электрон переходит из состояния n_i=1, чтобы указать n_f=2, затем рассчитайте длину волны электрона.

Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 10⁶м/с