Download Article
Download Article
Frequency, also called wave frequency, is a measurement of the total number of vibrations or oscillations made within a certain amount of time. There are a few different ways to calculate frequency based on the information you have available to you. Keep reading to learn some of the most common and useful versions.
-
1
Learn the formula. The formula for frequency, when given wavelength and the velocity of the wave, is written as: f = V / λ[1]
- In this formula, f represents frequency, V represents the velocity of the wave, and λ represents the wavelength of the wave.
- Example: A certain sound wave traveling in the air has a wavelength of 322 nm when the velocity of sound is 320 m/s. What is the frequency of this sound wave?
-
2
Convert the wavelength into meters, if necessary. If the wavelength is given in nanometers, you need to convert this value into meters by dividing it by the number of nanometers in a single meter.[2]
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 322 nm
- 322 nm x (1 m / 10^9 nm) = 3.22 x 10^-7 m = 0.000000322 m
Advertisement
-
3
Divide the velocity by the wavelength. Divide the velocity of the wave, V, by the wavelength converted into meters, λ, in order to find the frequency, f.[3]
- Example: f = V / λ = 320 / 0.000000322 = 993788819.88 = 9.94 x 10^8
-
4
Write your answer. After completing the previous step, you will have completed your calculation for the frequency of the wave. Write your answer in Hertz, Hz, which is the unit for frequency.
- Example: The frequency of this wave is 9.94 x 10^8 Hz.
Advertisement
-
1
Learn the formula. The formula for the frequency of a wave in a vacuum is almost identical to that of a wave not in a vacuum. Since there are no outside influences on the velocity of the wave, though, you would use the mathematical constant for the speed of light, which electromagnetic waves would travel at under these conditions. As such, the formula is written as: f = C / λ[4]
- In this formula, f represents frequency, C represents the velocity or speed of light, and λ represents the wavelength of the wave.
- Example: A particular wave of electromagnetic radiation has a wavelength of 573 nm when passing through a vacuum. What is the frequency of this electromagnetic wave?
-
2
Convert the wavelength into meters, if necessary. When the problem gives you the wavelength in meters, no further action is needed. If, however, the wavelength is given in micrometers, you need to convert this value into meters by dividing it by the number of micrometers in a single meter.
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 573 nm
- 573 nm x (1 m / 10^9 nm) = 5.73 x 10^-7 m = 0.000000573
-
3
Divide the speed of light by the wavelength. The speed of light is a constant, so even if the problem does not provide you with a value, the value remains 3.00 x 10^8 m/s. Divide this value by the wavelength converted into meters.[5]
- Example: f = C / λ = 3.00 x 10^8 / 5.73 x 10^-7 = 5.24 x 10^14
-
4
Write your answer. With this, you should have calculated the value of the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 5.24 x 10^14 Hz.
Advertisement
-
1
Learn the formula. Frequency and the time taken to finish a single wave oscillation are inversely proportional. As such, the formula for calculating frequency when given the time taken to complete a wave cycle is written as: f = 1 / T
- In this formula, f represents frequency and T represents the time period or amount of time required to complete a single wave oscillation.
- Example A: The time for a certain wave to complete a single oscillation is 0.32 seconds. What is the frequency of this wave?
- Example B: In 0.57 seconds, a certain wave can complete 15 oscillations. What is the frequency of this wave?
-
2
Divide the number of oscillations by the time period. Usually, you will be told how long it takes to complete a single oscillation, in which case, you would just divide the number 1 by the time period, T. If given a time period for numerous oscillations, however, you will need to divide the number of oscillations by the overall time period required to complete them.[6]
- Example A: f = 1 / T = 1 / 0.32 = 3.125
- Example B: f = 1 / T = 15 / 0.57 = 26.316
-
3
Write your answer. This calculation should tell you the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example A: The frequency of this wave is 3.125 Hz.
- Example B: The frequency of this wave is 26.316 Hz.
Advertisement
-
1
Learn the formula. When told the angular frequency of a wave but not the standard frequency of that same wave, the formula to calculate the standard frequency is written as: f = ω / (2π)[7]
- In this formula, f represents the frequency of the wave and ω represents the angular frequency. As with any mathematical problem, π stands for pi, a mathematical constant.
- Example: A particular wave rotates with an angular frequency of 7.17 radians per second. What is the frequency of that wave?
-
2
Multiply pi by two. In order to find the denominator of the equation, you need to double the value of pi, 3.14.
- Example: 2 * π = 2 * 3.14 = 6.28
-
3
Divide the angular frequency by the double of pi. Divide the angular frequency of the wave, given in radians per second, by 6.28, the doubled value of pi.[8]
- Example: f = ω / (2π) = 7.17 / (2 * 3.14) = 7.17 / 6.28 = 1.14
-
4
Write your answer. This final bit of calculation should indicate what the frequency of the wave is. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 1.14 Hz.
Advertisement
Add New Question
-
Question
What is the frequency if 80 oscillations are completed in 1 second?
Frequency is the number of oscillations completed in a second. The answer would be 80 Hertz.
-
Question
Do atoms have a frequency and, if so, does it mean everything vibrates?
Atoms have energy. Energy is often characterized as vibration. Vibration possesses frequency. So, yes, everything could be thought of as vibrating at the atomic level.
-
Question
What’s the definition of frequency?
The rate at which a vibration occurs that constitutes a wave, either in a material (as in sound waves), or in an electromagnetic field (as in radio waves and light), usually measured per second. The rate at which something occurs or is repeated over a particular period of time or in a given sample.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To calculate the frequency of a wave, divide the velocity of the wave by the wavelength. Write your answer in Hertz, or Hz, which is the unit for frequency. If you need to calculate the frequency from the time it takes to complete a wave cycle, or T, the frequency will be the inverse of the time, or 1 divided by T. Display this answer in Hertz as well. Keep reading to learn how to calculate frequency from angular frequency!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,513,328 times.
Did this article help you?
Как найти период и частоту колебаний
У любой волны, распространяющейся в той или иной среде, имеются три взаимосвязанных между собой параметра: длина, период колебаний и их частота. Любой из них можно найти, зная любой другой, при этом в некоторых случаях необходима также информация о скорости распространения колебаний в среде.

Инструкция
Независимо от того, какой из параметров вы собираетесь вычислять, переведите все исходные величины в систему СИ. Тогда и результат получится в единицах той же системы. При необходимости пользуйтесь калькулятором, способным, помимо мантиссы, отображать и порядок числа, поскольку при решении задач по теме «Колебания и волны» приходится иметь дело как с очень малыми, так и с очень большими величинами.
В случае если известны длина волны и скорость распространения колебаний, частоту вычислите следующим образом:
F=v/λ, где F — частота (Гц), v — скорость распространения колебаний в среде (м/с), λ — длина волны (м).
Скорость света в вакууме обычно обозначают другой буквой — c (латинской). Помните, что скорость распространения света в любой другой среде, кроме вакуума, меньше скорости света в вакууме. Если та или иная частица пролетает через среду со скоростью, хотя и меньшей скорости света в вакууме, но большей скорости света в этой среде, возникает так называемое свечение Черенкова.
Если известна частота, период найти можно и в том случае, если скорость распространения колебаний неизвестна. Формула для вычисления периода по частоте выглядит следующим образом:
T=1/F, где T — период колебаний (с), F — частота (Гц).
Из сказанного выше следует, что найти частоту, зная период, можно также без информации о скорости распространения колебаний. Способ ее нахождения такой же:
F=1/T, где F — частота (Гц), T — период колебаний (с).
Для того чтобы узнать циклическую частоту колебаний, вначале вычислите их обычную частоту любым из указанных выше способов. Затем умножьте ее на 2π:
ω=2πF, где ω — циклическая частота (радиан в секунду), F — обычная частота (Гц).
Отсюда следует, что для вычисления обычной частоты при наличии информации о циклической следует воспользоваться обратной формулой:
F=ω/(2π), где F — обычная частота (Гц), ω — циклическая частота (радиан в секунду).
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
— скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
— скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
— число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Скорость света в веществе с показателем преломления, равным n (также безразмерная величина), вычислите, поделив скорость света на показатель преломления.
После окончания вычислений при необходимости переведите результат из системы СИ в удобные для вас единицы измерения.
Источники:
- как будет изменяться период колебаний
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Частота (или частота волны) — это число полных колебаний или циклов волны, совершенных в единицу времени. Есть несколько различных способов вычислить частоту в зависимости от данной вам информации.
-
1
Формула: f = V / λ[1]
- где f — частота, V — скорость волны, λ — длина волны.
- Пример: вычислите частоту звуковой волны, если длина волны равна 322 нм, а скорость звука равна 320 м/сек.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.[2]
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 322 нм
- 322 нм x (1 м / 10^9 нм) = 3,22 x 10^-7 м = 0,000000322 м
-
3
Разделите скорость волны на ее длину. Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах.[3]
- Пример: f = V / λ = 320 / 0.000000322 = 993788819,88 = 9,94 x 10^8
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 9,94 х 10^8 Гц.
Реклама
-
1
Формула: f = C / λ. Формула для вычисления частоты волны в вакууме практически идентична формуле для вычисления частоты волны в средах. В вакууме не существует факторов, влияющих на скорость волны, поэтому в формуле используется постоянная величина скорости света, с которой распространяются электромагнитные волны в вакууме.[4]
- В формуле f — частота, С — скорость света, λ — длина волны.
- Пример: вычислите частоту электромагнитной волны, если ее длина равна 573 нм.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 573 нм
- 573 нм х ( 1 м / 10^9 нм) = 5,73 х 10^-7 м = 0,000000573
-
3
Разделите скорость света на длину волны. Скорость света является постоянной величиной, которая равна 3,00 х 10^8 м/с. Разделите эту величину на длину волны (в метрах).[5]
- Пример: f = С / λ = 3,00 х 10^8 / 5,73 х 10^-7 = 5,24 х 10^14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 5,24 х 10^14 Гц.
Реклама
-
1
Формула: f = 1 / T.[6]
Частота обратно пропорциональна времени, которое необходимо для совершения одного колебания волны.- В формуле f — частота, Т — время, которое необходимо для совершения одного колебания волны.
- Пример А: вычислите частоту волны, если ей необходимо 0,32 с для совершения одного колебания.
- Пример B: за 0,57 секунд волна совершает 15 колебаний. Вычислите частоту этой волны.
-
2
Разделите число колебаний на время. Если в задаче дано время, затрачиваемое на 1 колебание, то в этом случае просто разделите 1 на время (Т). Если в задаче дано время, затрачиваемое на несколько колебаний, то в этом случае разделите данное количество колебаний (n) на время (Т).[7]
- Пример А: f = 1 / T = 1 / 0,32 = 3,125
- Пример B : f = n / T = 15 / 0,57 = 26,316
-
3
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример А: частота волны равна 3,125 Гц.
- Пример B: частота волны равна 26,316 Гц.
Реклама
-
1
Формула: f = ω / (2π)[8]
- где f — частота, ω — угловая частота, π — число Пи (математическая константа).
- Пример: волна вращается с угловой частотой 7,17 радиан в секунду. Вычислите частоту этой волны.
-
2
Умножьте Пи на два.
- Пример: 2 * π = 2 * 3,14 = 6,28
-
3
Разделите угловую частоту (в радианах в секунду) на удвоенное число пи (6,28).[9]
- Пример: f = ω / (2π) = 7,17 / (2 * 3,14) = 7,17 / 6,28 = 1,14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота волны равна 1,14 Гц.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 114 081 раз.
Была ли эта статья полезной?
Длина, скорость и частота электромагнитной волны.
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
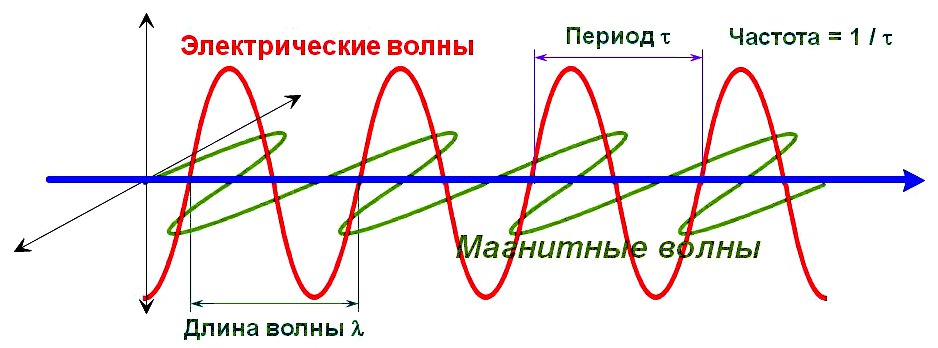
Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.
Рис.1
Длина волны, обозначаемая буквой λ и измеряемая в метрах —
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 — это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.
Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
|
Частота электромагнитных колебаний f |
||
Показатель преломления среды (по умолч. 1) |
||
Длина волны |
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
|
Длина электромагнитной волны в вакууме λ |
||
Частота |
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.
Формула частоты в физике
Формула частоты
Определение
Частота — это физический параметр, которые используют для характеристики периодических процессов.
Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
[nu =frac{1}{T}left(1right).]
Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
[nu =frac{N}{Delta t}left(2right),]
где $Delta t$ — время за которое происходят $N$ колебаний.
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
[left[nu right]=с^{-1}=Гц.]
Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:
[{nu =nu }_1- {nu }_2left(3right).]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:
[{omega }_0=2pi nu left(4right).]
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]
где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(8right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(9right).]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.
[nu =frac{N}{Delta t}left(1.1right).]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:
[nu =frac{600}{60}=10 left(Гцright).]
Ответ. $nu =10Гц$
Пример 2
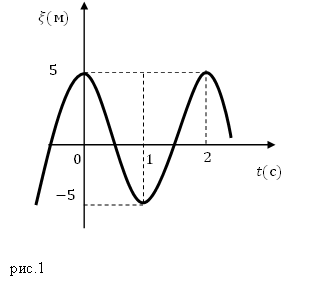
Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $xi left(tright)={xi }_{max}=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
[T=2 left(cright).]
Частота — величина обратная периоду колебаний, значит:
[nu =frac{1}{T}=0,5 left(Гцright).]
Ответ. 1) ${xi }_{max}=5 (м)$. 2) $nu =0,5$ Гц
Читать дальше: формулы математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!