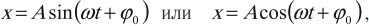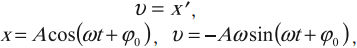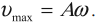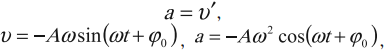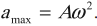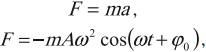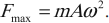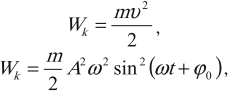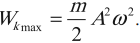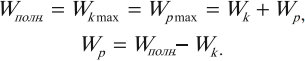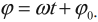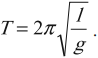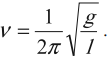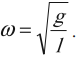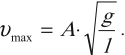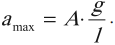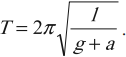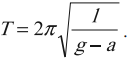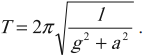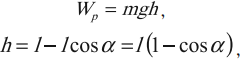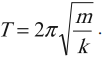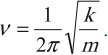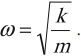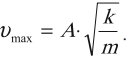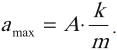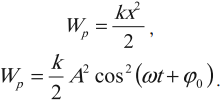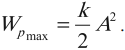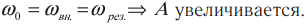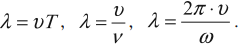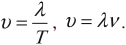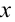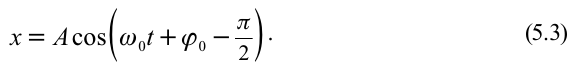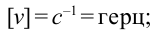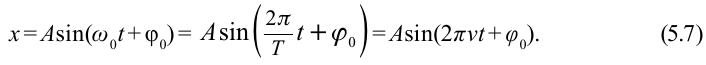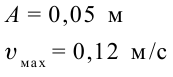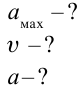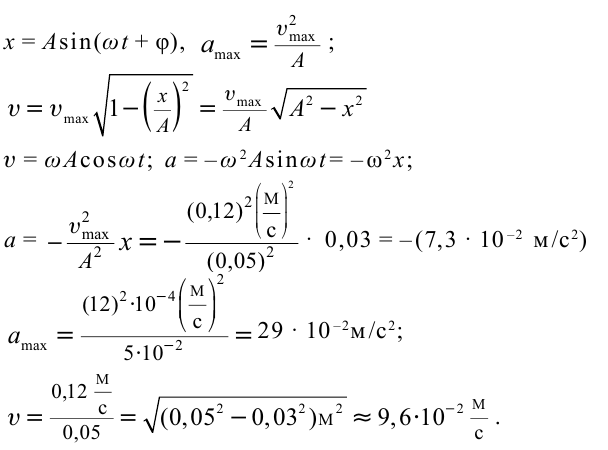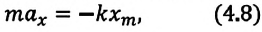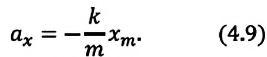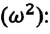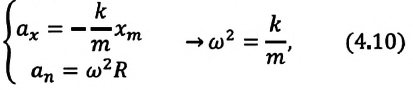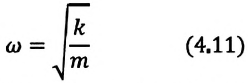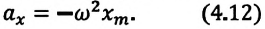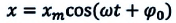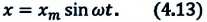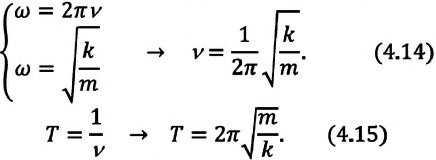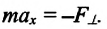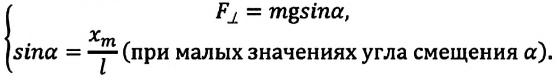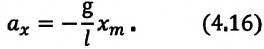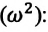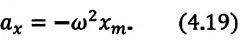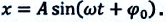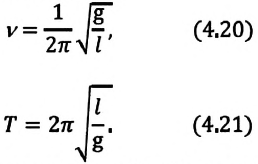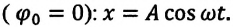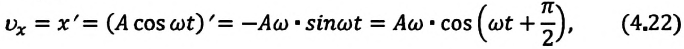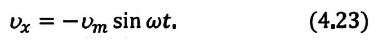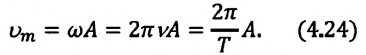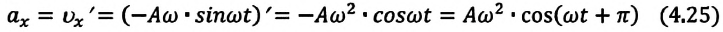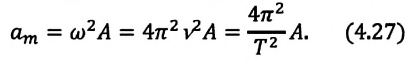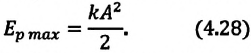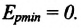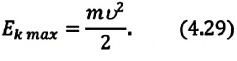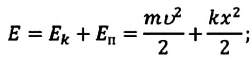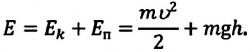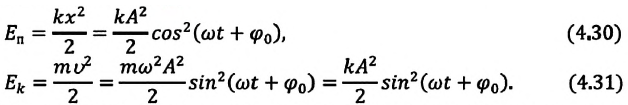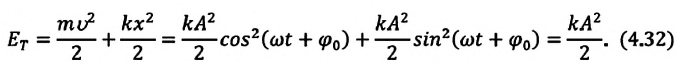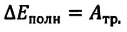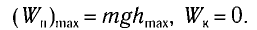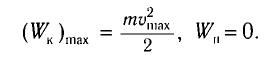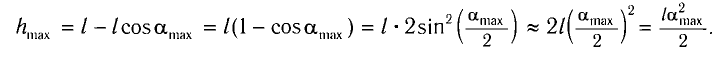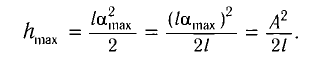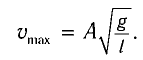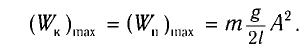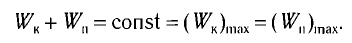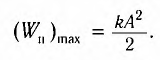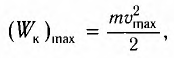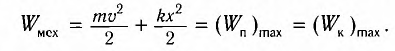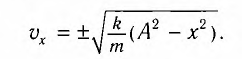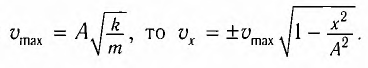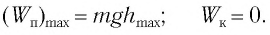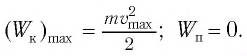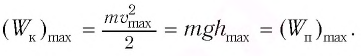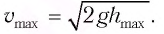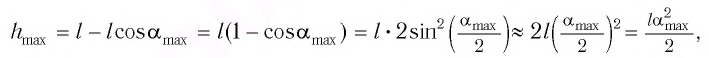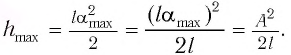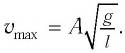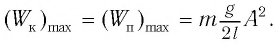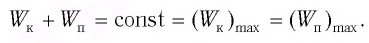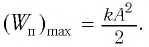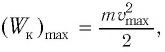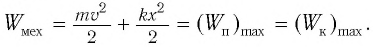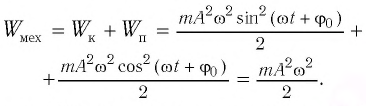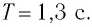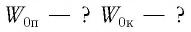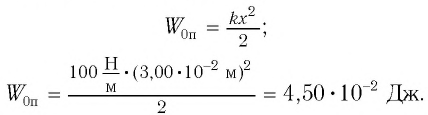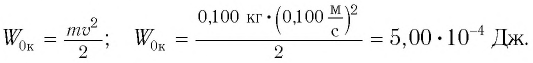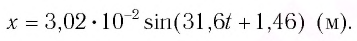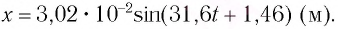Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.
Уравнение вида:
$frac{d^2x}{dt^2}+omega^2x=0 (1),$
где $omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия
называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.
Решением уравнения (1) можно считать функции:
$x=Asin (omega t+varphi)$ или
$x=Acos (omega t+varphi_1)$,
где $A$ — амплитуда колебаний.
Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить
- малое тело, подвешенное на упругую пружину (Пружинный маятник);
- физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
- математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 1
Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.
В полной механической энергии гармонического осциллятора выделяют:
- потенциальную энергию;
- и кинетическую энергию.
Потенциальная энергия
Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.
Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;
$F=-kx(2)$
и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-frac{dU}{dx}$), потенциальную энергию линейного осциллятора определим как:
«Энергия гармонических колебаний» 👇
$U(x)=frac{kx^2}{2}=frac{momega^2x^2}{2}=frac{mA^2omega_0^2}{2}cos^2 (omega t+varphi)= frac{mA^2omega_0^2}{4}(1+cos 2(omega t +varphi)) (3).$
Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2omega$.
Кинетическая энергия.
Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:
$E_k=frac{mv^2}{2}=frac{mdot{x}^2}{2}=frac{mA^2omega_0^2}{2}sin^2 (omega t+varphi) =frac{mA^2omega_0^2}{4}(1-cos 2(omega t +varphi)) (4).$
Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2omega$ (эта частота в два раза больше, чем частота колебаний $x$)
Закон сохранения энергии при гармонических колебаниях
Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:
$frac{mdot{x}^2}{2}+frac{momega^2x^2}{2}=frac{momega^2A^2}{2}=const$.
Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.
Закон сохранения энергии позволяет сделать два существенных вывода
Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.
Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.
Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.
$frac{mV^2}{2}=frac{momega^2A^2}{2}(5),$
где $V$ — максимальная скорость.
Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.
Средняя кинетическая энергия.
Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:
$f_{sr}=frac{1}{t_2-t_1}int_1^2f(t)dt (6),$
где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.
Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.
Замечание 1
Площадь под осью $t$ считают отрицательной.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
Запишем закон движения осциллятора как:
$x(t)=Acos (omega t+varphi) (7)$,
его скорость равна:
$dot{x}=-Aomegasin (omega t+varphi) (8).$
Выражение для потенциальной энергии представим как:
$U(t) = frac{omega^2A^2}{2}cos^2 (omega t+varphi) (9)$.
Кинетическую энергию представит выражение:
$E_k=frac{omega^2A^2}{2}sin^2 (omega t+varphi) $
Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $cos^2 (omega t+varphi)$ и $sin^2 (omega t+varphi)$:
$(sin^2 (omega t+varphi))_{sr}=frac{1}{T}int_0^T cos^2 (omega t+varphi)dt=frac{1}{T}int_0^Tfrac{1}{2}(1-cos 2(omega t+varphi)dt)=frac{1}{2},$
где $T$ — период колебаний; $omega T=2pi.$
По аналогии получаем:
$sin^2 (omega t+varphi)_sr=frac{1}{2}.$
В результате имеем:
-
средняя по времени потенциальная энергия гармонического колебания за один период равна:
$U_{sr}=frac{momega^2A^2}{4}(10),$
-
средняя по времени кинетическая энергия составила:
$E_{k,sr}=frac{momega^2A^2}{4}(11)$.
Сравнивая (10) и (11) мы видим, что:
$U_{sr}= E_{k,sr}=frac {1}{2}E$,
где $E$ — полная механическая энергия гармонических колебаний.
то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
-
Колебания.
-
Механические
колебания. -
Превращения
энергии при механических колебаниях. -
Период колебаний.
-
Частота колебаний.
-
Циклическая
частота колебаний. -
Амплитуда
механических колебаний. -
Гармонические
колебания. -
Фаза гармонического
колебания. -
Аналитическое
представление колебаний. -
Графическое
представление колебаний. -
Скорость точки в
гармоническом колебании. -
Ускорение точки
в гармоническом колебании. -
Динамика
гармонического колебания. -
Период колебаний
пружинного маятника. -
Математический
маятник. Квазиупругая сила. -
Колебания тела,
плавающего на поверхности жидкости. -
Колебания однородной
жидкости в U
– образной трубке. -
Колебания тела в
сферической чаше. -
Энергия гармонического
колебания. -
Затухающие
колебания. -
Вынужденные
колебания. -
Резонанс.
-
Свободные колебания.
Собственная частота. -
Автоколебания.
1. Колебания.
Колебаниями
вообще называют периодические изменения
состояния системы, при которых периодически
изменяются значения различных физических
величин, характеризуют данную систему.
Например, периодические изменения
давления и плотности воздуха, напряжения
и силы электрического тока есть колебания
этих величин.
Математически
периодичность означает, что, если
— есть периодическая функция времени с
периодом Т,
то при любом t
выполняется
равенство
2. Механические
колебания
– движения тела, которые точно или почти
точно повторяются через равные интервалы
времени.
Механические
колебания возникают в системах, имеющих
положение устойчивого равновесия.
Согласно с принципом минимума потенциальной
энергии, в положении устойчивого
равновесия потенциальная энергия
системы минимальна. Когда тело выводят
из положения устойчивого равновесия,
его потенциальная энергия возрастает.
При этом возникает сила, направленная
к положению равновесия (возвращающая
сила), и чем дальше от положения равновесия
отклоняется тело, тем больше его
потенциальная энергия и тем больше
модуль возвращающей силы. Например, при
отклонении пружинного маятника от
положения равновесия, роль возвращающей
силы играет сила упругости, модуль
которой изменяется пропорционально
отклонению
,
где х
отклонение маятника от положения
равновесия. Потенциальная энергия
пружинного маятника изменяется
пропорционально квадрату смещения
.
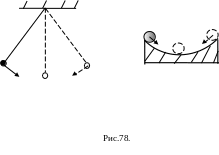
Аналогично возникают
колебания нитяного маятника и шарика,
движущегося по дну сферической чаши
радиуса R,
который можно рассматривать как нитяной
маятник с длиной нити равной радиусу
чаши (Рис.78).
3.Превращения
энергии при механических колебаниях.
Если отсутствуют силы трения, то полная
механическая энергия тела, совершающего
колебательное движение, остаётся
постоянной. В процессе колебаний
происходят периодические взаимные
превращения потенциальной и кинетической
энергии тела. Проведем рассуждения на
примере колебаний нитяного маятника .
Для упрощения рассуждений примем
потенциальную энергию маятника в
положении равновесия равной нулю. В
крайнем отклонённом положении
потенциальная энергия маятника
максимальна, а кинетическая энергия
равна нулю, т.к. в этом положении маятник
находится в покое. При движении к
положению равновесия высота маятника
над поверхностью Земли уменьшается,
уменьшается и потенциальная энергия,
при этом возрастают его скорость и
кинетическая энергия. В положении
равновесия потенциальная энергия равна
нулю, а кинетическая энергия максимальна.
Продолжая движение по инерции, маятник
проходит положение равновесия. После
прохождения положения равновесия
кинетическая энергия маятника убывает,
но возрастает его потенциальная энергия.
Когда произойдёт остановка маятника,
его кинетическая энергия станет равной
нулю, а потенциальная энергия достигнет
максимума и всё повторится в обратном
порядке.
По закону сохранения
энергии потенциальная энергия маятника
в крайнем отклоненном положении равна
его кинетической в момент прохождения
положения равновесия.
В процессе колебаний
в любой момент времени полная механическая
энергия маятника равна его потенциальной
в крайнем отклонённом положении или
кинетической энергии в момент прохождения
положения равновесия
где
высота
маятника в крайнем отклоненном положении,
скорость
в момент прохождения положения
равновесия.
4. Период
колебания
– минимальный интервал времени , через
который происходит повторение движения,
или интервал времени, в течение которого
происходит одно полное колебание. Период
(Т)
измеряется в секундах.
5. Частота
колебании
—
определяет число полных колебаний,
совершаемых за одну секунду. Частота и
период связаны соотношением
,
.
Частота измеряется
в герцах (Гц). Один герц – одно полное
колебание совершаемое за одну секунду
6. Циклическая
частота или круговая частота
определяет число полных колебаний,
свершаемых за
секунд
.
Частота – величина
положительная
,
.
7. Амплитуда
механических колебаний
– максимальное отклонение тела от
положения равновесия. В общем случае
колебаний амплитуда есть максимальное
значение, которое принимает периодически
изменяющаяся физическая величина.
8. Гармонические
колебания
– колебания, в которых колеблющаяся
величина изменяется по закону синуса
или косинуса (по гармоническому закону):
Здесь
амплитуда
колебаний,
циклическая
частота.
9
.
Фаза
гармонического колебания –
величина
,
стоящая под
знаком синуса или косинуса. Фаза
определяет значение колеблющейся
величины в данный момент времени,
начальная
фаза, т.е. в момент начала отсчёта времени
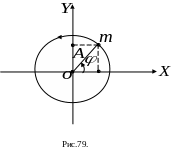
Простейшим
примером гармонических колебаний
является колебание проекции на оси
координат точки m
движущейся равномерно по окружности
радиуса А
в плоскости XOY,
центр которой совпадает с началом
координат (рис. 79)
Для простоты
положим
,
т.е.
тогда
Многие известные
колебательные системы можно лишь
приближенно считать гармоническими
лишь приближенно при очень малых
отклонениях. Главным условием
гармонического колебания является
постоянство циклической частоты и
амплитуды. Например, при колебаниях
нитяного маятника, угол отклонения от
вертикали изменяется неравномерно,
т.е. циклическая частота
не постоянна. Если отклонения очень
малы, то движение маятника происходит
очень медленно и неравномерностью
движения можно пренебречь, полагая
.
Чем медленнее движение, тем меньше
сопротивление среды, те меньше потери
энергии и меньше изменения амплитуды.
Итак, малые колебания
можно приближенно считать гармоническими.
1
0.
Аналитическое
представление колебаний
– запись колеблющейся величины в виде
функции
,
выражающей зависимость величины от
времени.
11. Графическое
представление колебаний – представление
колебаний
в виде графика функции
в координатных осях OX
и t
.
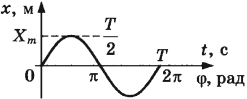
Например, аналитически
гармоническое колебания записывается
в виде
,
а его графическое представление
изображается синусоидой — сплошная
линия на Рис.80.
12.
Скорость точки при гармоническом
колебании
– получим, дифференцируя по времени
функцию х(t)
,
где
амплитуда скорости, пропорциональна
циклической частоте и амплитуде смещения.
Итак, скорость V
по синусоидальному закону с таким же
периодом T,
что и смещение
х
в пределах
.
Фаза скорости
опережает фазу смещения на
.
Это значит, что скорость максимальна,
когда точка проходит положение равновесия
,
а при максимальных смещениях точки
её скорость равна нулю . График скорости
представлен пунктирной линией на рис
Рис.80
13. Ускорение
точки при гармонических колебаниях
получим,
дифференцируя скорость по времени или
дифференцируя смещение х
дважды по времени :
,
где
— амплитуда ускорения пропорциональная
амплитуде смещения и квадрату циклической
частоты.
У
скорение
точки при гармонических колебаниях
изменяется по синусоидальному закону
с тем же периодом Т,
что и смещение в пределах
Фаза ускорения опережает фазу смещения
на
.
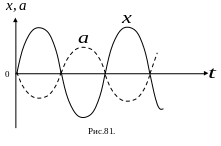
Ускорение равно нулю в момент прохождения
точкой положения равновесия, На Рис.81
график ускорения изображен пунктирной
линией, сплошная линия изображает
график смещения.
Учитывая, что
ускорение запишем в виде
,
т.е. ускорение в
гармоническом колебании пропорционально
смещению и всегда направлено к положению
равновесия ( против смещения). Удаляясь
от положения равновесия точка движется
ускоренно, приближаясь к положению
равновесия точка движется ускоренно.
14. Динамика
гармонического колебания.
Умножив ускорение точки, совершающей
гармоническое колебание, на её массу
получим согласно второму закону Ньютона
силу, действующую на точку
Обозначим
Теперь запишем силу, действующую на
точку
.
Из последнего равенства
следует, что гармонические колебания
вызываются силой пропорциональной
смещению и направленной против смещения,
т.е. к положению равновесия.
15. Период
колебаний пружинного маятника. Пружинный
маятник совершает колебания под
действием силы упругости
.
Сила пропорциональная
смещению и направленная к положению
равновесия вызывает гармонические
колебания точки. Поэтому колебания
пружинного маятника гармонические.
Коэффициент жесткости равен
.
Помня, что
получим период свободных колебаний
пружинного маятника
.
Частота пружинного
маятника равна
.
1
5.
Математический
маятник –
материальная точка, подвешенная на
бесконечно тонкой, невесомой, нерастяжимой
нити, совершающая колебания в вертикальной
плоскости, под действием силы тяжести.
Груз, подвешенный
на нити, размеры которого пренебрежимо
малы по сравнению с длиной нити , можно
приближенно считать математическим
маятником. Часто такой маятник называют
нитяным маятником.
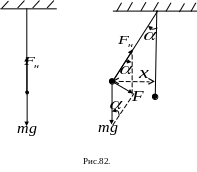
Рассмотрим малые
колебания математического маятника
длиной l.
В положении равновесия сила тяжести
уравновешена силой натяжения нити,
т.е.
.
Если отклонить
маятник на малый угол
,
то сила тяжести и сила натяжения,
направленные под углом друг к другу, в
сумме дают равнодействующую силу
,которая
направлена к положению равновесия. На
Рис.82 отклонение маятника от вертикали
равно
.
Угол
настолько мал, что циклическую частоту,
т.е. угловую скорость вращения нити
можно считать постоянной. Поэтому
и смещение маятника запишем в виде
.
Таким образом,
малые колебания математического маятника
есть гармонические колебания. Из Рис.
82 следует, что сила
,
но
,
следовательно
,
где m,
g,
и l
постоянные величины. Обозначим
и получим модуль возвращающей силы в
виде
.
Если учесть, что сила
всегда направлена к положению равновесия,
т.е. против смещения, то её выражение
запишем в виде
.
Итак, сила, вызывающая
колебания математического маятника
пропорциональна смещению и направлена
против смещения, как при колебаниях
пружинного маятника, т.е характер этой
силы такой же как и силы упругой. Но по
природе упругая сила есть сила
электромагнитная. Сила же вызывающая
колебания математического маятника по
своей природе есть сила гравитационная
– неэлектромагнитная поэтому её называют
квазиупругой
силой. Любая сила, которая действует
как сила упругая, по природе не является
электромагнитной, называется квазиупругой
силой. Это позволяет нам записать
выражение периода колебаний математического
маятника в виде
.
Из этого равенства
следует, что период колебаний
математического маятника не зависит
от массы маятника, но зависит от его
длины и ускорения свободного падения.
Зная период колебаний математического
маятника и его длину, можно определить
ускорение свободного падения в любой
точке на поверхности Земли.
17. Колебания
тела, плавающего на поверхности жидкости.
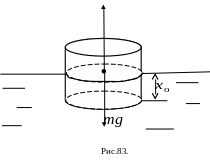
Для простоты
рассмотрим тело массы m
в форме цилиндра с площадью основания
S.
Тело плавает
частично погрузившись в жидкость,
плотность которой
(Рис.
83).
Пусть в положении
равновесия глубина погружения
.
При этом равнодействующая силы Архимеда
и силы тяжести
равна нулю
.
Если изменить
глубину погружения на х
то сила Архимеда станет равной
и модуль равнодействующей силы F
станет отличен от нуля
Учитывая, что
получим
.
Обозначая
,
модуль силы F
в виде
.
Если глубина
погружения увеличивается, т.е. тело
смещается вниз, сила Архимеда становится
больше силы тяжести и равнодействующая
F
направлена вверх, т.е. против смещения.
Если же глубина погружения уменьшается
, т.е. смещается вверх от положения
равновесия, сила Архимеда становится
меньше силы тяжести и равнодействующая
F
направлена вниз, т.е. против смещения.
Итак, сила F
всегда направлена против смещения и
её модуль пропорционален смещению
.
Э
та
сила квазиупругая и она вызывает
гармонические колебания тела, плавающего
на поверхности жидкости. Период этих
колебаний вычисляется по общей для
гармонических колебаний формуле
.
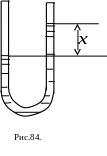
18. Колебания
однородной жидкости в U-трубке.
Пусть однородная жидкость массы m,
плотность которой
налита
в U
– образную трубку, площадь сечения
которой S
(Рис.84) В состоянии равновесия высоты
столбов в обоих коленах трубки одинаковы,
по закону сообщающихся сосудов для
однородной жидкости.
Если жидкость
вывести из состояния равновесия, то
высоты столбов жидкости в коленах будут
периодически изменяться, т.е. жидкость
в трубке будет совершать колебан
ия.
Пусть в некоторый
момент времени высота столба жидкости
в правом колене на х
больше . чем в левом. Это значит, что на
жидкость в трубке действует сил тяжести
жидкости в столбе высотой х,
,
где
— объём столба жидкости высотой x.
Произведение
величина постоянная, следовательно
.
Таким образом,
модуль силы F
пропорционален разности высот столбов
жидкости в коленах, т.е. пропорционален
смещению жидкости в трубке. Направление
этой силы всегда противоположно смещению,
т.е.
.
Следовательно
эта сила вызывает гармонические колебания
жидкости в трубке. Период этих колебаний
запишем по правилу для гармонических
колебаний
.
19. Колебания
тела в сферической чаше.
Пусть тело скользит без трения в
сферической чаше радиуса R
(Рис. 78). При малых отклонениях от положения
равновесия колебания этого тела можно
рассматривать как гармонические
колебания математического маятника,
длина которого равна R,
с периодом равным
.
20. Энергия
гармонического колебания.
В качестве примера рассмотрим колебания
пружинного маятника. При смещении х
его потенциальная энергия равна
.
В
этот же момент его кинетическая энергия
равна
.
Учитывая, что
получим
полную механическую энергию маятника
.
Или подставив
,
.
Эта формула
позволяет вычислить полную механическую
энергию любой системы, совершающей
гармонические колебания.
21. Затухающие
колебания.
Механические колебания происходят в
средах, оказывающих сопротивление
движению. Поэтому энергия колебательного
движения расходуется на работу по
преодолению сил трения.
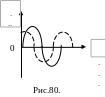
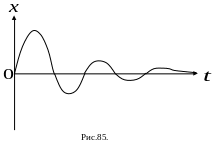
Е
сли
силы трения не очень велики, то амплитуда
колебаний постепенно уменьшается и
колебания прекратятся. График затухающего
колебания представлен на Рис. 85. Это
периодическое движение, амплитуда
которого постепенно уменьшается.
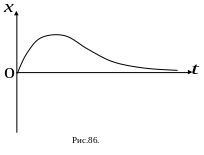
Если сила трения
очень велика, то затухающие колебания
не происходят. Тело , выведенное из
положения равновесия какими-либо силами,
после прекращения действия этих сил
возвращается в положение равновесия и
останавливается. Такое движение
называется апериодическим (непериодическим).
График апериодического движения
представлен на Рис.86.
2
2.
Вынужденные
колебания
– незатухающие колебания системы,
которые вызываются внешними периодически
меняющимися с течением времени силами
( вынуждающие силы).
Если вынуждающая
сила изменяется по гармоническому
закону
,
где
амплитуда
вынуждающей силы,
её
циклическая частота, то в системе могут
установиться вынужденные гармонические
колебания с циклической частотой равной
частоте вынуждающей силы
.
23. Резонанс
– резкое возрастание амплитуды
вынужденных колебаний при совпадении
частоты вынуждающей силы с частотой
свободных колебаний системы
.
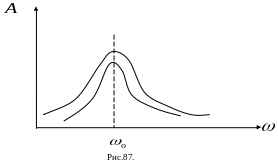
Если колебание происходит в среде,
оказывающей сопротивление, то график
зависимости амплитуды вынужденных
колебаний от частоты вынуждающей силы
выглядит так как на Рис.87
Вынуждающая сила,
частота которой совпадает с частотой
свободных колебаний системы, даже при
очень малых амплитудах вынуждающей
силы может вызвать колебания с очень
большой амплитудой.
24. Свободные
колебания. Собственная частота системы.
Свободными колебаниями называют
колебания системы, происходящие под
действием её внутренних сил. Для
пружинного маятника внутренней силой
является сила упругости. Для математического
маятника, который состоит из самого
маятника и Земли, внутренней силой
является сила тяжести. Для тела, плавающего
на поверхности жидкости, внутренней
силой является сила Архимеда.
25. Автоколебания
– незатухающие
колебания, происходящие в среде, за счет
источника энергии не обладающего
колебательными свойствами, компенсирующего
потери энергии на преодоление сил
трения. Автоколебательные системы
получают равные порции энергии через
равные интервалы времени например,
через один период. Примером автоколебательной
системы являются часы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
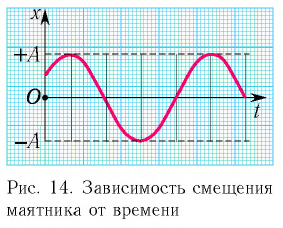
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
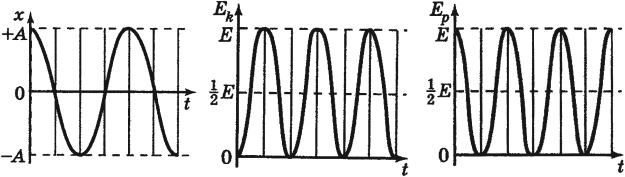
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
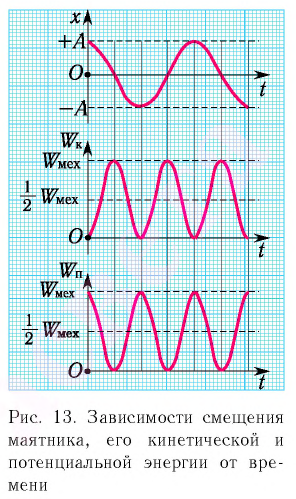
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
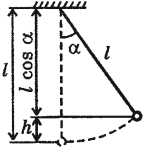
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
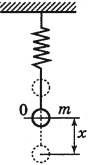
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
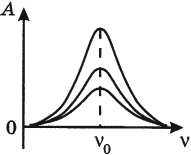
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
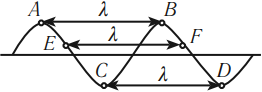
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
3 (59.1%) 156 votes
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
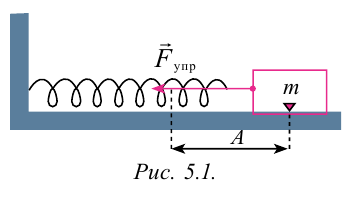
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 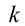
Если груз, который находится в равновесии, потянем вправо на расстояние 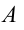
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
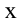
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 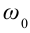
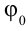
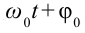
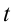
Из математики известно, что 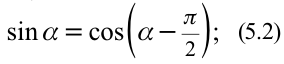
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 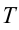

б) частота колебания 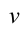
Единица
c) циклическая частота 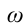
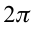
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
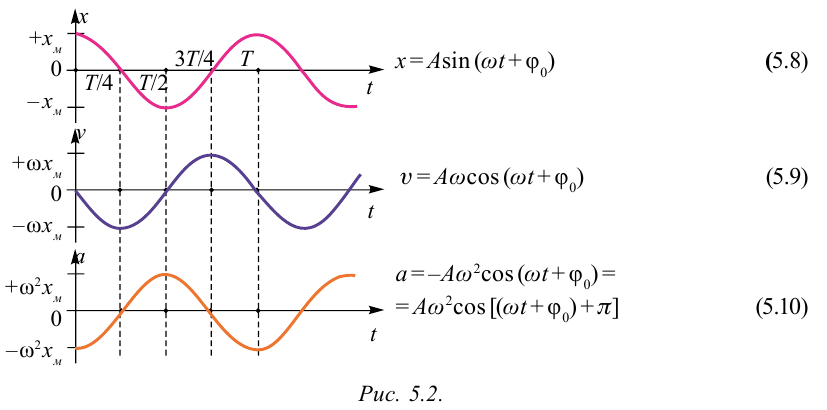
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
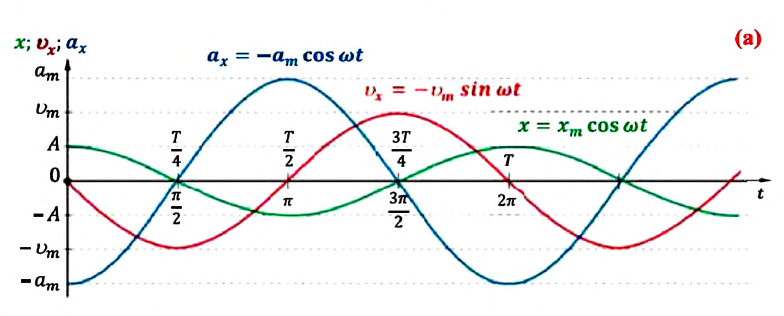
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
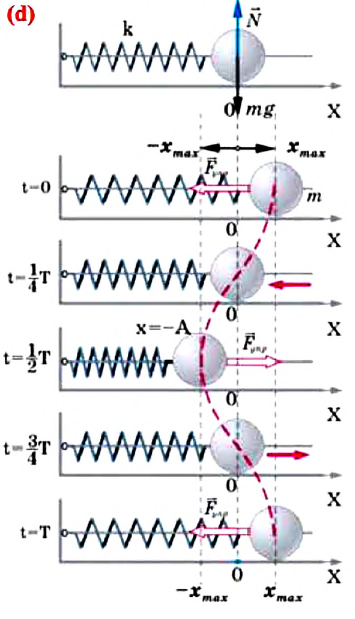
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 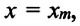
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 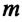
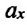
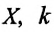
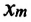
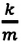
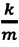
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 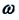
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 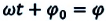
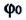
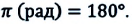
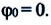

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 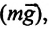
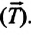
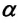
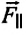
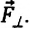
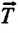
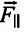
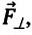
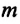
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 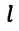
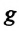
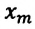
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 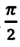
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 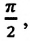
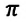
Превращения энергии при гармонических колебаниях
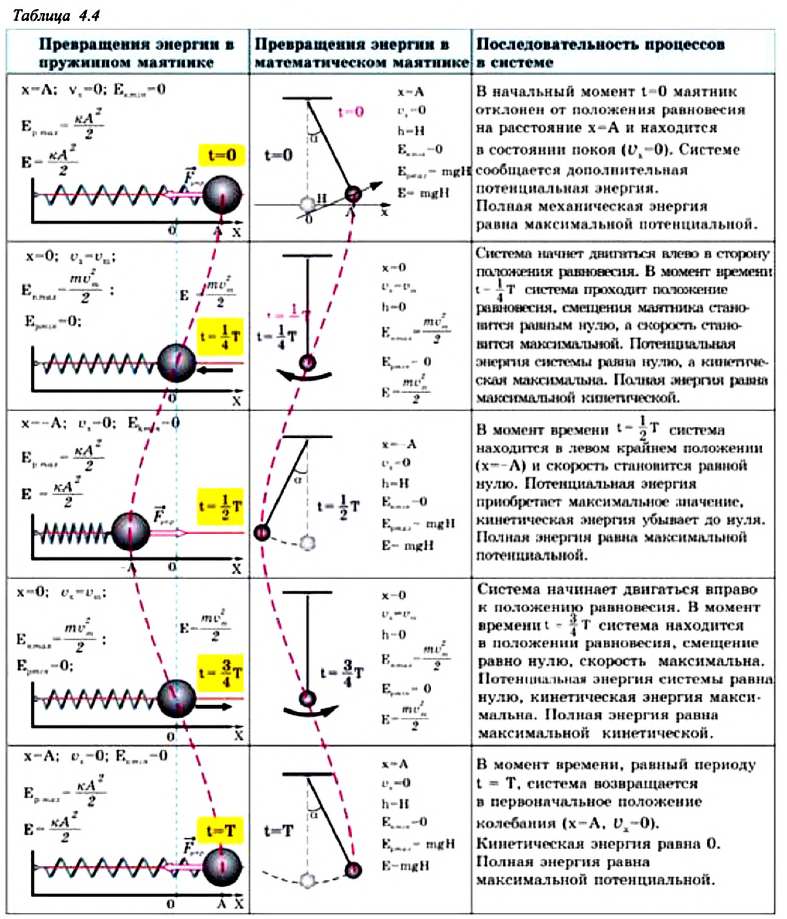
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 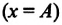
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 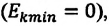
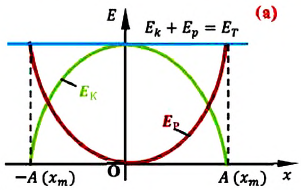
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 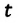
a) для пружинного маятника:
b) для математического маятника:
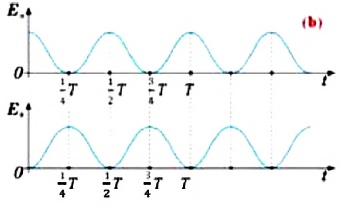
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
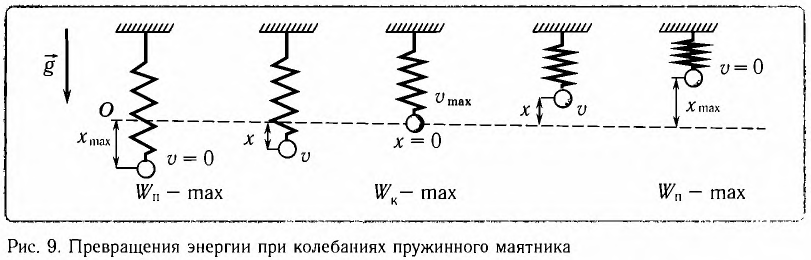
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
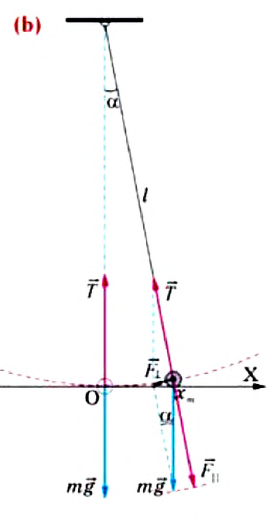
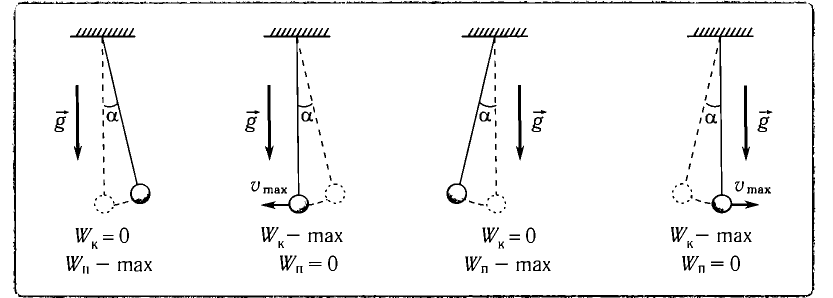
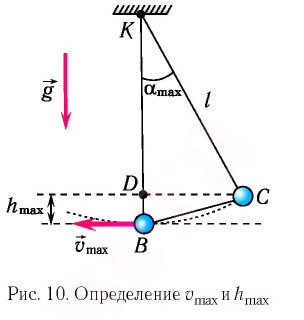
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
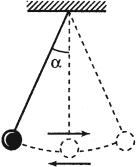
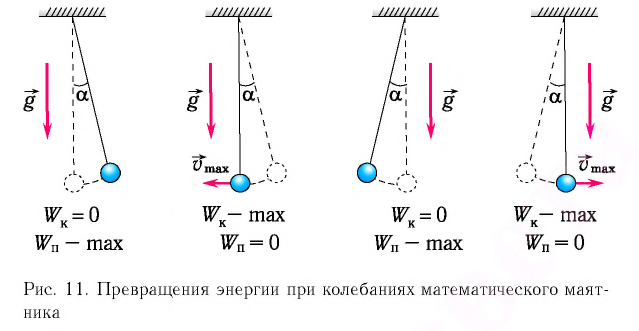
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
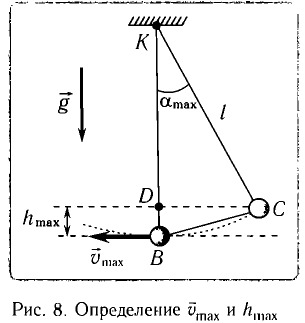
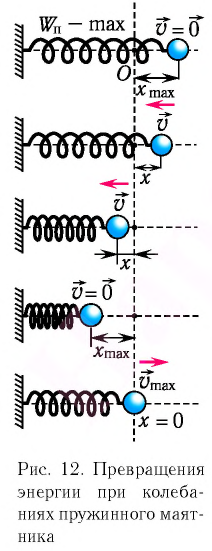
Из закона сохранения механической энергии следует (рис. 8), что
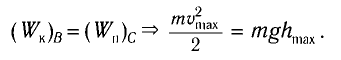
Отсюда найдем модуль максимальной скорости маятника:
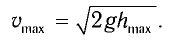
Высоту 
Если колебания малые, то 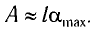
Отсюда
Подставив выражение для 
Подставляя выражения для 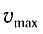

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 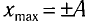
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 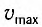
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 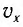
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 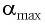
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 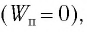
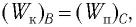
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 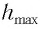
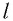
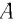
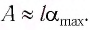
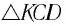
или
Подставив выражение (3) для 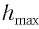
Подставляя выражения (3) для 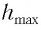
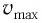
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 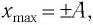
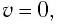
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 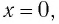
где 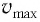
В положениях между крайними точками полная энергия
С учетом выражений для координаты 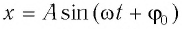
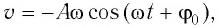
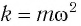
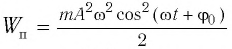
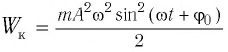
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 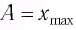
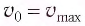
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 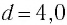
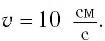
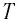
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 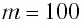
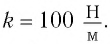
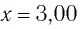
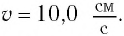
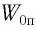
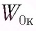
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 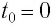
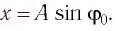
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
Частота колебаний, теория и онлайн калькуляторы
Частота колебаний
Гармонические колебания, частота и др их характеристики
Определение
Колебаниями называют такие движения или процессы, которые повторяются.
По своей природе колебания делят на механические, электромагнитные и др. Разные виды колебаний описывают при помощи одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания являются свободными (собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешние воздействия на эту систему отсутствуют.
Самым простым видом колебаний являются гармонические колебания. Гармоническими колебаниями называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:
[s=A{cos ({omega }_0t+varphi ) } left(1right),]
где $A=s_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ — фаза колебаний. Величина $s$ лежит в пределах $-Ale sle $+A.
Промежуток времени через который повторяются определенные состояния системы (T) называют периодом. За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(2right).]
Разные процессы, повторяющиеся через равные промежутки времени (периодические процессы) можно представить в виде совокупности наложенных гармонических колебаний.
Определение частоты колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $). Частота колебаний — это количество полных колебаний, которые совершаются за единицу времени.
[nu =frac{1}{T}left(3right).]
Из (2) и (3) следует, что циклическая частота равна:
[{omega }_0=2pi nu left(4right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса называется в честь немецкого ученого Г. Герца.
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота дискретных событий, частота вращения
Определение
Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(5right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(6right).]
Примеры задач с решением
Пример 1
Задание. Каковы: циклическая частота колебаний и частота колебаний величины $r$, если ее гармонические колебания заданы уравнением:
[r=0,5{cos left(3pi t+frac{pi }{4}right)(м) . }]
Решение.Рассмотрим уравнение колебаний параметра $r$:
[r=0,5{cos left(3pi t+frac{pi }{4}right)left(мright)(1.1) . }]
Из этого уравнения мы видим, что амплитуда колебаний равна $r_{max}=0,5 (м)$; ${omega }_0=3pi $ ($frac{рад}{с}$). Частоту колебаний ($nu $) найдем, используя формулу:
[{omega }_0=2pi nu left(1.2right).]
Выразим $nu $, имеем:
[nu =frac{{omega }_0}{2pi } left(1.3right).]
Подставляя ${omega }_0=3pi $textit{ }($frac{{rm рад}}{{rm с}}$) получаем:
[nu =frac{3pi }{2pi }=frac{3}{2}left(Гцright).]
Ответ. ${omega }_0=3pi $ $frac{рад}{с};;$ $nu $=1,5 Гц
Пример 2
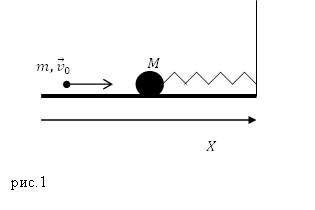
Задание. Шар массой $M$ закреплен на пружине коэффициент упругости, которой равен $k$. Шар лежит на гладкой горизонтальной поверхности (рис.1). Горизонтально летела пуля, ее скорость составляла $v_0 $, была направлена в сторону шара и в момент удара была параллельна оси пружины, масса пули $m$. После удара о шар пуля застряла в нем. Какова частота колебаний шара, вызванных ударом пули. Шар может скользить по столу без трения. Массу пружины и сопротивление воздуха не учитывать.
Решение. После того, как пуля ударила по шарику и застряла в нем, данная система будет совершать колебания. Так как по условию задачи колебания можно считать свободными (трения нет), то колебания шарика (с пулей) на пружине являются свободными и гармоническими, их можно описать как, например изменение координаты шарика, который примем за материальную точку:
[x=x_m{sin left({omega }_0t+varphi right)left(2.1right). }]
В таких колебаниях кинетическая энергия переходит в потенциальную энергию и наоборот, поэтому можно записать закон сохранения энергии в виде:
[frac{(m+M)v^2_m}{2}=frac{kx^2_m}{2} left(2.2right),]
где $frac{(m+M)v^2_m}{2}$ — кинетическая энергия системы в момент, сразу следующий за ударом, скорость шарика с пулей максимальна; $frac{kx^2_m}{2}$ — потенциальная энергия сжатой пружины в момент максимального ее сжатия, когда шарик с пулей перестаёт двигаться.
Амплитуду скорости колебаний найдем как:
[v_x=frac{dx}{dt}=frac{d}{dt}(x_m{sin left({omega }_0t+varphi right)=x_m{omega }_0{cos left({omega }_0t+varphi right)to v_m= }x_m{omega }_0(2.3). }]
Подставим $v_m$ в (2.2), имеем:
[frac{(m+M){x_m}^2{{omega }_0}^2}{2}=frac{kx^2_m}{2}to {omega }_0=sqrt{frac{k}{m+M}}left(2.4right).]
Применим выражение:
[nu =frac{{omega }_0}{2pi } left(2.5right).]
Найдем частоту колебаний системы:
[nu =frac{1}{2pi }sqrt{frac{k}{m+M}}.]
Ответ. $nu =frac{1}{2pi }sqrt{frac{k}{m+M}}$
Читать дальше: частота.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!