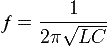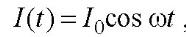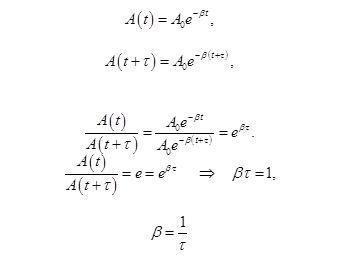Как найти частоту колебаний контура формула - Исправление недочетов и поиск решений вместе с Examum.ru

Выберите подписку для получения дополнительных возможностей Kalk.Pro

Любая активная подписка отключает

рекламу на сайте

- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов
- Доступ к скрытым чертежам
- Безлимитные сохранения расчетов

Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.

Подробнее с подписками можно ознакомиться здесь.

Источник

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчёт частоты:

Частота резонанса колебательного контура LC.
ƒ = 1/(2π√(LC))

Расчёт ёмкости:

Ёмкость для колебательного контура LC
C = 1/(4π²ƒ²L)

Расчёт индуктивности:

Индуктивность для колебательного контура LC
L = 1/(4π²ƒ²C)

Похожие страницы с расчётами:

Рассчитать импеданс.

Рассчитать реактивное сопротивление.

Рассчитать реактивную мощность и компенсацию.

Замечания и предложения принимаются и приветствуются!

Источник

Электромагнитные колебания

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Колебательный контур
Энергетические превращения в колебательном контуре
Электромеханические аналогии
Гармонический закон колебаний в контуре
Вынужденные электромагнитные колебания

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур

Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.

Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.

Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.

Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.

Начальный момент: t=0 . Заряд конденсатора равен q_0 , ток через катушку отсутствует (рис. 1). Конденсатор сейчас начнёт разряжаться.

Рис. 1. t=0

Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.

Аналогия. Маятник оттянут вправо на величину x_0 и в начальный момент отпущен. Начальная скорость маятника равна нулю.

Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен . Ток через катушку нарастает (рис. 2).

Рис. 2.

Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.

Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины (она же — координата маятника) уменьшается.

Конец первой четверти : t = T/4 . Конденсатор полностью разрядился. Сила тока достигла максимального значения I_0 (рис. 3). Сейчас начнётся перезарядка конденсатора.

Рис. 3. t = T/4

Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.

Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения v_0 . Деформация пружины равна нулю.

Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4).

Рис. 4.

Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.

Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.

Конец второй четверти t = T/2 . Конденсатор полностью перезарядился, его заряд опять равен q_0 (но полярность другая). Сила тока равна нулю (рис. 5). Сейчас начнётся обратная перезарядка конденсатора.

Рис. 5. t = T/2

Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна x_0 .

Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6).

Рис. 6.

Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.

Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен I_0 , но на сей раз имеет другое направление (рис. 7).

Рис. 7.

Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью v_0 , но на сей раз в обратном направлении.

Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8).

Рис. 8.

Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.

Конец четвёртой четверти и всего периода: t = T . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9).

Рис. 9. t = T

Данный момент идентичен моменту t = 0 , а данный рисунок — рисунку 1. Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.

Аналогия. Маятник вернулся в исходное положение.

Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!

Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.

В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.

Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.

к оглавлению ▴

Энергетические превращения в колебательном контуре

Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна .

Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.

Возьмём момент времени, когда заряд конденсатора максимален и равен q_0 , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия контура сосредоточена в конденсаторе:

$W = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}}.$

Теперь, наоборот, рассмотрим момент, когда ток максимален и равен I_0 , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:

$W = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$

В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток , энергия контура равна:

$W = frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}}.$

Таким образом,

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle q_0^2}{displaystyle 2C vphantom{1^a}} = frac{displaystyle LI_0^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Соотношение (1) применяется при решении многих задач.

к оглавлению ▴

Электромеханические аналогии

В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.

Для пружинного маятника мы имеем соотношение, аналогичное (1):

$frac{displaystyle kx^2}{displaystyle 2 vphantom{1^a}} + frac{displaystyle mv^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle kx_0^2}{displaystyle 2 vphantom{1^a}} = frac{displaystyle mv_0^2}{displaystyle 2 vphantom{1^a}}.$ (2)

Здесь, как вы уже поняли, — жёсткость пружины, — масса маятника, и — текущие значения координаты и скорости маятника, x_0 и v_0 — их наибольшие значения.

Сопоставляя друг с другом равенства (1) и (2), мы видим следующие соответствия:

(3)

(4)

(5)

(6)

Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.

В самом деле, период колебаний пружинного маятника, как мы знаем, равен:

$T = 2 pi sqrt{frac{displaystyle m}{displaystyle k}}.$

B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность , а жёсткость на обратную ёмкость 1/c . Получим:

(7)

Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.

к оглавлению ▴

Гармонический закон колебаний в контуре

Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».

Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.

Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10).

Рис. 10. Положительное направление обхода

Сила тока считается положительной (I > 0) , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной (I < 0) .

Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае — заряд левой пластины конденсатора.

При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться ). Действительно, знаки обеих частей совпадают: если I > 0 , то заряд левой пластины возрастает, и потому .

Величины и меняются со временем, но энергия контура остаётся неизменной:

$frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}} + frac{displaystyle LI^2}{displaystyle 2 vphantom{1^a}} = W = const.$ (8)

Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8); не забываем, что слева дифференцируются сложные функции (Если — функция от , то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна: ${(y^2)}$ ):

$frac{displaystyle 2q dot{q}}{displaystyle 2C vphantom{1^a}}+frac{displaystyle L cdot 2I dot{I}}{displaystyle 2 vphantom{1^a}} = W =0.$

Подставляя сюда и , получим:

$frac{displaystyle qI}{displaystyle C vphantom{1^a}} + LI ddot{q} = 0,$

$Ileft ( frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} right ) = 0.$

Но сила тока не является функцией, тождественно равной нулю; поэтому

$frac{displaystyle q}{displaystyle C vphantom{1^a}} + L ddot{q} = 0.$

Перепишем это в виде:

$ddot{q} + frac{displaystyle 1}{displaystyle LC vphantom{1^a}}q = 0.$ (9)

Мы получили дифференциальное уравнение гармонических колебаний вида $ddot{q} + omega^2_0 q = 0$ , где . Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:

$omega_0 = frac{displaystyle 1}{displaystyle sqrt{LC} vphantom{1^a}}.$ (10)

Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:

$T = frac{displaystyle 2 pi}{displaystyle omega_0 vphantom{1^a}}= 2 pisqrt{LC}.$

Мы снова пришли к формуле Томсона.

Гармоническая зависимость заряда от времени в общем случае имеет вид:

(11)

Циклическая частота omega_0 находится по формуле (10); амплитуда q_0 и начальная фаза alpha определяются из начальных условий.

Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при t = 0 заряд конденсатора максимален и равен q_0 (как на рис. 1); ток в контуре отсутствует. Тогда начальная фаза , так что заряд меняется по закону косинуса с амплитудой q_0 :

$q = q_0 cos omega_0t = q_0 cos left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (12)

Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12), опять-таки не забывая о правиле нахождения производной сложной функции:

$I = dot{q} = -q_0 omega_0 sin omega_0t.$

Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:

$I = -I_0 sin omega_0t = -I_0 sin left ( frac{displaystyle t}{displaystyle sqrt{LC} vphantom{1^a}} right ).$ (13)

Амплитуда силы тока равна:

$I_0 = q_0 omega_0 = frac{displaystyle q_0}{displaystyle sqrt{LC} vphantom{1^a}}.$

Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2).

Ток течёт в отрицательном направлении: I < 0 . Поскольку , фаза колебаний находится в первой четверти: . Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13).

А теперь посмотрите на рис. 8. Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!

Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13). Для наглядности представим эти графики в одних координатных осях (рис. 11).

Рис. 11. Графики колебаний заряда и тока

Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.

Используя формулу приведения

$cos left ( varphi + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = - sin varphi,$

запишем закон изменения тока (13) в виде:

$I = -I_0 sin omega_0 t = I_0 cos left ( omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная $omega_0 t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}}$ , больше фазы заряда на величину pi/2 . В таком случае говорят, что ток опережает по фазе заряд на pi/2 ; или сдвиг фаз между током и зарядом равен pi/2 ; или разность фаз между током и зарядом равна pi/2 .

Опережение током заряда по фазе на pi/2 графически проявляется в том, что график тока сдвинут влево на pi/2 относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз pi/2 ).

к оглавлению ▴

Вынужденные электромагнитные колебания

Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.

Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12).

Рис. 12. Вынужденные колебания

Если напряжение источника меняется по закону:

то в контуре происходят колебания заряда и тока с циклической частотой omega (и с периодом, соответственно, ). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте $omega_0 = 1/sqrt{LC}$ .

Амплитуда вынужденных колебаний заряда и тока зависит от частоты omega : амплитуда тем больше,чем ближе omega к собственной частоте контура omega_0 .При наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитные колебания» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Параллельный и последовательный колебательный контур

Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных
параметров. Онлайн калькулятор резонансной
частоты колебательного контура,
добротности и коэффициента затухания в зависимости от величин индуктивности,
ёмкости и сопротивления потерь

Колебательный контур – это пассивная электрическая цепь, состоящая из конденсатора и катушки индуктивности, в которой
возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный
контур называется последовательным.

Для начала рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного
чаще последовательного.

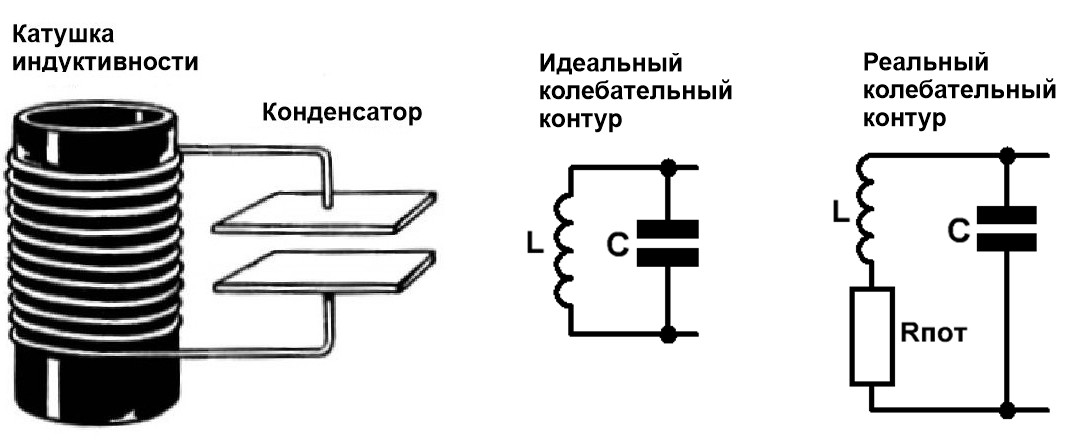
Рис.1 Параллельный колебательный контур, его изображение на схеме (идеальный
колебательный контур), реальный колебательный контур

При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного
сопротивления потерь катушки – Rпот.
Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).

Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.

Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)

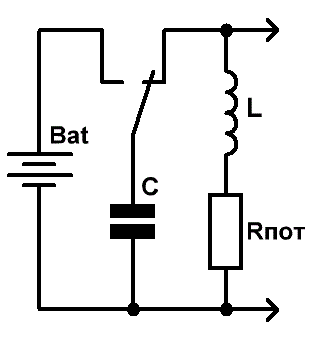
Рис.2 Колебательный процесс в параллельном колебательном контуре

Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд
q_max от внешнего источника Bat напряжением
U_max.
После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие
электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).

Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь,
суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу
колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в
еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её
измерить, имеет смысл посетить страницу – ссылка на страницу.

А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.

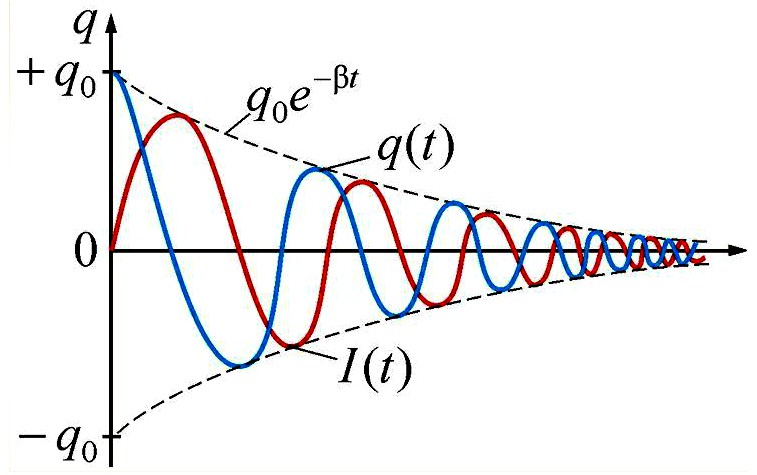
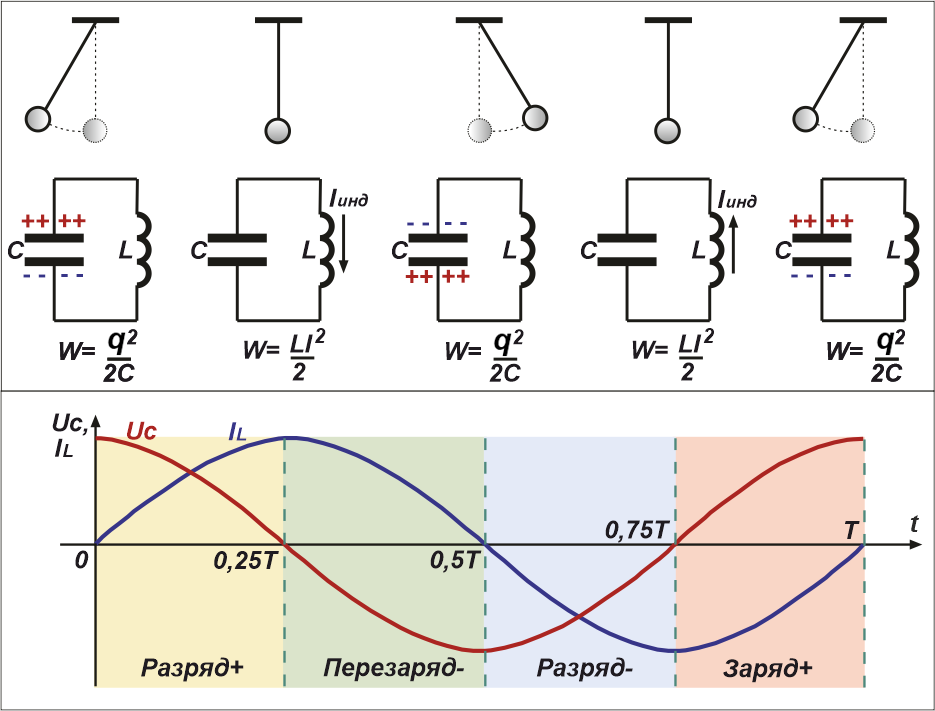
Рис.3 Фазы колебаний, происходящих в колебательном контуре за полный период

Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.

Опишем стадии колебательного процесса за полный период колебаний:

1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна
W = q²/2C ).
Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС
самоиндукции, препятствующая этому росту.

2. t = 0,25Т – конденсатор полностью разряжен.
Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки
W = L*I²/2.
Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.

3. t = 0,5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через
катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.

4. t = 0,75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен
в противоположную (по отношению к п.2) сторону.

5. t = Т – всё начинается сначала, т. е. аналогично 1п.

А теперь – формулы, которые могут понадобиться при расчёте колебательного LC контура:

Период колебаний: T₀ = 2π√LC ;

Частота: F₀ = 1/T₀ ;

Круговая (циклическая) частота: ω₀ = 2π/T₀ =
2πF₀ ;

Максимальный заряд конденсатора: q_max = U_maxC ;

Максимальная сила тока через катушку: I_max = ωq_max .

Добротность колебательного контура:
;

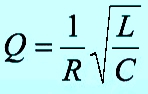
Мгновенные значения напряжения, силы тока и энергии можно рассчитать по формулам:

Заряд: q(t) = q_max cos(ωt) ;

Напряжение: U(t) = U_max cos(ωt) ;

Сила тока: I(t) = I_max sin(ωt) ;

Энергия: W(t) = I(t)²L/2 + q(t)²/(2C) .

Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров
(с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания
β и логарифмический декремент колебаний λ.

Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно
пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в
е раз.
Для колебательного контура данная величина вычисляется по формуле:
β = R_потерь /(2L).

Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения
двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент колебаний равен коэффициенту затухания,
умноженному на период колебаний:
λ = βT.

С учётом коэффициента затухания наши формулы приобретают следующий вид:

Заряд: q(t) = q_max cos(ωt) e^(-βt) ;

Напряжение: U(t) = U_max cos(ωt) e^(-βt) ;

Сила тока: I(t) = I_max sin(ωt) e^(-βt) ;

Энергия: W(t) = I(t)²L/2 + q(t)²/(2C) ;

Период:
;

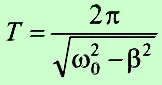
Круговая (циклическая) частота:
;

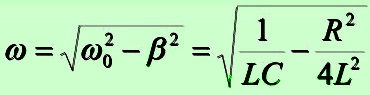
Добротность: Q = Lω/R .

При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие
β² << ω₀², круговая частота контура равна
ω ≈ ω₀ ,
а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.

Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.

РАСЧЁТ РЕЗОНАНСНОЙ ЧАСТОТЫ, ДОБРОТНОСТИ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОНТУРА

Ёмкость конденсатора контура
Индуктивность катушки контура L
Сопротивление потерь Rпот

Резонансная частота
Добротность = кол-во колебаний
Коэффициент затухания β (сек^-1)

Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые
выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и
имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.

А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.

Источник

63.
Колебательный
контур —
простейшая
система, в которой могут
происходить свободные электромагнитные колебания.
Электрическая
цепь,
содержащая соединённые катушку
индуктивности и конденсатор.
В такой цепи могут
возбуждаться колебания тока (и напряжения).

Резонансная
частота контура
определяется так называемой формулой
Томсона:

Электромагнитными
колебаниями являются радиоволны,
микроволны, инфракрасное излучение,
видимый свет, ультрафиолетовое излучение,
рентгеновские лучи, гамма-лучи.

Электромагнитные
колебания возникают
в колебательном контуре, состоящем из
конденсатора и катушки индуктивности,
присоединённой к обкладкам конденсатора.
Процесс возбуждения электромагнитных
колебаний в контуре сопровождается
периодическим изменением заряда и
напряжения на обкладках конденсатора
и силы тока, протекающего через
индуктивность.

При
колебательном процессе энергия
электрического поля заряженного
конденсатора W_Э=С
U²/2
преобразуется в энергию магнитного
поля в катушке индуктивности W_М=
L I²/2
и обратно.

Период
и частота собственных колебаний в
контуре определяются формулами:

64. Рассмотрим
колебательный контур, состоящий из
конденсатора емкости C и катушки
индуктивности L. Если в начальный момент
времени конденсатор С имеет заряд q0, то
в контуре возникнут электромагнитные
колебания. Заряд q на конденсаторе
изменяется от времени t по гармоническому
закону:

где q0 — амплитуда
колебаний заряда, ω — собственная
частота колебаний.

Период T собственных
электромагнитных колебаний в колебательном
контуре выражается формулой Томсона:

Частота v
электромагнитных колебаний равна:

Переменным
электрическим током называется ток I,
который изменяется во времени по
гармоническому закону:

где I0 — амплитуда
колебаний тока, ω — частота переменного
тока.

В случае переменного
тока напряжение U прямо пропорционально
силе тока I:где
Z — коэффициент пропорциональности,
называемый импедансом. Его можно записать
в виде:

где XR = R — активное
сопротивление,

— емкостное
сопротивление,

— индуктивное
сопротивление.

Отметим, что
переменный ток в отличии от постоянного
течет через конденсатор. При высоких
частотах ω емкостное сопротивление
падает почти до нуля, а индуктивное
значительно возрастает. При низких
частотах соответственно наоборот.

Средняя за период
мощность P в цепи переменного тока
определяется формулой:

где I0, U0 — амплитуды
силы тока и напряжения соответственно.

Отметим, что
мощность выделяется только на активном
сопротивлении.

Пусть у нас имеется
нагрузка сопротивлением R. Действующим
(эффективным) значением силы переменного
тока IД называется величина, при которой
на нагрузке R при постоянной силе тока
IД выделяется мощность, равная средней
мощности нашего переменного тока. Можно
доказать, что

Аналогичным образом
дается определение действующего
(эффективного) напряжения:

Трансформатор —
это устройство, предназначенное для
преобразования напряжения переменного
тока. Он состоит из магнитного сердечника,
первичной и вторичной обмоток. Пусть
первичная обмотка содержит n1 витков, а
вторичная — n2. Если мы подадим на
первичную обмотку напряжение U1 то во
вторичной обмотке индуцируется напряжение
U2. Они связаны следующей формулой:

Колебания,
амплитуда которых из-за потерь энергии
реальной колебательной системы
уменьшается с течением времени,
называются затухающими.

Наиболее
часто встречается случаи, когда сила
сопротивления пропорциональна скорости
движения

где r — коэффициент сопротивления среды.
Знак минус показывает, что FC направлена
в сторону противоположную скорости.

Запишем
уравнение колебаний в точке, колеблющийся
в среде, коэффициент сопротивлений
которой r. По второму закону Ньютона

где
β — коэффициент затухания. Этот коэффициент
характеризует скорость затухания
колебаний, При наличии сил сопротивления
энергия колеблющейся системы будет
постепенно убывать, колебания будут
затухать.

—
дифференциальное уравнение затухающих
колебаний.

—
уравнение затухающих колебаний.

ω
– частота затухающих колебаний

Период
затухающих колебаний

Затухающие
колебания при строгом рассмотрении не
являются периодическими. Поэтому о
периоде затухаюших колебаний можно
говорить, когда β мало.

Если
затухания выражены слабо (β→0), то
. Затухающие колебания можно рассматривать
как гармонические колебания, амплитуда
которых меняется по экспоненциальному
закону

В
уравнении (1) А0 и φ0 — произвольные
константы, зависящие от выбора момента
времени, начиная е которого мы рассматриваем
колебания

Рассмотрим
колебание в течение, некоторого времени
τ, за которое амплитуда уменьшится в е
раз

τ
— время релаксации.

Коэффициент
затихания β обратно пропорционален
времени, в течение которого амплитуда
уменьшается в е раз. Однако коэффициента
затухания недостаточна для характеристики
затуханий колебаний. Поэтому необходимо
ввести такую характеристику для затухания
колебаний, в которую входит время одного
колебаний. Такой характеристикой
является декремент (по-русски: уменьшение)
затуханияD, который равен отношению
амплитуд, отстоящих по времени на период:

Логарифмический
декремент затухания равен логарифму
D:

Логарифмический
декремент затухания обратно пропорционален
числу колебаний, в результате которых
амплитуда колебаний уменьшилась в
е раз. Логарифмический декремент
затухания — постоянная для данной системы
величина.

Еще
одной характеристикой колебательной
система является добротность Q.

Добротность

Добротность
пропорциональна числу колебаний,
совершаемых системой, за время релаксации
τ.
Добротность
Q колебательной системы является мерой
относительной диссипации (рассеивания)
энергии.Добротность Q колебательной
системы называется число, показывающее
во сколько раз сила упругости больше
силы сопротивления.Чем больше добротность,
тем медленнее происходит затухание,
тем затухающие колебания ближе к
свободным гармоническим.

66.
Вынужденные
колебания –
колебания, происходящие под действием
меняющейся во времени внешней силы,
которая совершает работу. За счет этого
энергия колебательной системы
увеличивается. Такой процесс можно
описывать как процесс притока энергии
в систему извне в ходе самих колебаний.
Примером систем, в которых происходят
вынужденные колебания, являются качели,
раскачиваемые человеком, груз, висящий
на пружине, точку подвеса которой
периодически поднимают и опускают.

Если
внешняя сила, действующая на систему,
изменяется с течением времени по закону
косинуса или синуса, то возникающие в
системе вынужденные колебания будут
гармоническими. При этом частота
вынужденных колебаний будет совпадать
с частотой изменения внешней силы.

Если
при вынужденных колебаниях энергия,
поступающая непрерывно или периодически
от внешнего источника, восполняет
потери, возникающие за счет работы силы
трения, то колебания оказываются незатухающими.

Амплитуда
вынужденных колебаний определяется
амплитудой колебаний внешней силы, а
также соотношением между частотой
изменения этой силы и собственной
частотой колебательной системы.

При
вынужденных колебаниях может наблюдаться
явление резкого возрастания
амплитуды A вынужденных
колебаний системы – резонанс. Это
явление возникает тогда, когда частота
вынуждающей силы приближается к
собственной частоте колебаний этой
системы. При этом энергия, поступающая
в колебательную систему, также равна
потерям энергии за счет работы силы
трения, однако баланс энергий наступает
при другой амплитуде колебаний.

Резонанс
может возникать и тогда, когда частота
колебаний вынуждающей силы кратна
собственной частоте колебаний системы.

Зависимость
амплитуды колебаний системы от частоты
вынуждающей силы (рис. 7) называется
резонансной кривой.

67.
В
плоской волне всем точкам среды, лежащим
в любой плоскости, перпендикулярной
направлению распространения волны, в
каждый момент времени соответствуют
одинаковые смещения и скорости частиц
среды. Таким образом, все величины,
характеризующие плоскую волну, являются
функциями времени и только одной
координаты, например, х,
если ось Ох совпадает
с направлением распространения волны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник