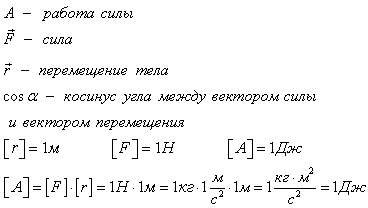Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
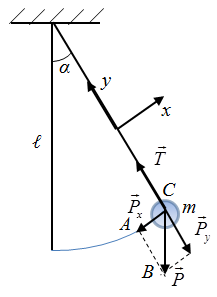
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
-
Математический маятник. Частота колебаний математического маятника (формула).
Математический
маятник —
материальная точка, подвешенная на
невесомой нерастяжимой нити, и совершавшая
колебания в вертикальной плоскости под
действием силы тяжести. Если отклонить
маятник от положения равновесия,
то сила
тяжести и сила
упругости будут
направлены под углом. Равнодействующая
сила уже
не будет равна нулю. Под воздействием
этой силы маятник устремится к положению
равновесия, но по инерции движение
продолжится и маятник отклоняется в
другую сторону. Равнодействующая сила
его снова возвращает.
Частота
математического маятника —
Чем больше период колебаний математического
маятника, тем меньше частота.
Важно
где происходят колебания! На Луне и на
Земле один и тот же математический
маятник при одинаковых начальных
условиях колебаться будет по-разному.
Так как ускорение
свободного падения на
Луне отличается от ускорения свободного
падения на Земле.
-
Линейная скорость материальной точки, линейное ускорение материальной точки, единицы измерения. Сложение скоростей.
линейная
скорость
— это производная от пройденного пути
по времени.
Отдельные
точки вращающегося тела имеют различные
линейные скорости
(метр/сек).
Скорость каждой точки, будучи направлена
по касательной к соответствующей
окружности, непрерывно изменяет свое
направление. Величина
скорости определяется
скоростью вращения тела и
расстоянием R рассматриваемой точки от
оси вращения. Пусть за малый промежуток
времени тело
повернулось на угол
Точка, находящаяся на расстоянии R от
оси проходит при этом путь, равный :
Линейная
скорость точки по определению:
|
|
линейное
ускорение
— это производная от скорости по времени.
Формула
линейного ускорения:
a
= dv/dt = d2s/dt2,
где s – путь,пройденный телом.
Сложение
скоростей —
с помощью данного закона определяется
скорость движения тела относительно
неподвижной системы отсчёта. Она равна
векторной сумме скорости этого тела
относительно подвижной системы отсчета
и скорости самой подвижной системы
отсчета относительно неподвижной
системы
Для
того, чтоб было более понятно, как
работает закон сложения скоростей,
рассмотрим такой пример. Вагон движется
со скоростью 50 кмч (это будет ),
в вагоне идет человек со скоростью 3
кмч (это будет ),
найти скорость человека относительно
Земли.
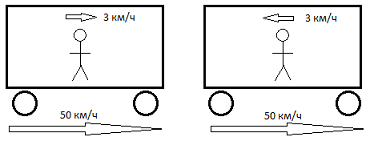
данной задачи будет два решения. Если
человек будет идти по направлению
движения вагона, то скорость человека
относительно Земли будет 53 кмч.
А
если человек будет идти против движения
вагона, то скорость человека относительно
Земли будет 47 кмч.
В
Формуле мы использовали :
—
Конечная
скорость тела
— Скорость
тел в различных инерциальных системах
отчета
-
Свободные колебания. Пружинный маятник. Частота колебаний пружинного маятника (формула).
Колебания
называются свободными
(или собственными), если они совершаются
за счет первоначальной сообщенной
энергии при последующем отсутствии
внешних воздействий на колебательную
систему (систему, совершающую колебания).
Пружинный
маятник —
это груз массой т,
подвешенный на абсолютно упругой пружине
и совершающий гармонические колебания
под действием упругой
силы F = –kx, где k — жесткость
пружины.
Частота
пружинного маятника — Чем больше
период колебаний пружинного маятника,
тем меньше частота
—
Частота
Пружинного маятника,
— Период
колебаний маятника
—
Масса
груза, или масса маятника,
—
Жесткость пружины
-
Угловая
скорость, частота вращения, период
вращения (определение, единицы измерения,
связь между величинами). Связь между
линейной и угловой скоростями.
Угловая
скорость численно равна углу поворота
радиуса за единицу времени.
Период
и частота
Период
вращения T —
это время, за которое тело совершает
один оборот.
Частота
вращение — это количество оборотов за
одну секунду.
Частота
и период взаимосвязаны соотношением
Связь
с угловой скоростью
Линейная
скорость точки.
Направление вектора линейной скорости
всегда совпадает с касательной к
окружности
Точка,
лежащая на окружности радиусом R,
за один оборот пройдет путь .
Поскольку время одного оборота тела
есть период T,
то модуль линейной скорости точки можно
найти так:
Так
как ,
то
-
Условия
возникновения затухающих колебаний
(соотношение между собственной частотой
и коэффициентом затухания). Амплитуда
затухающих колебаний (формула).
Соотношение:
β — коэффициент затухания. Этот коэффициент
характеризует скорость затухания
колебаний, При наличии сил сопротивления
энергия колеблющейся системы будет
постепенно убывать, колебания будут
затухать.
Амплитуда колебаний —
это максимальное расстояние, на
которое удаляется
колеблющееся тело от своего положения
равновесия. Амплитуда
затухающих колебаний изменяется по
закону ,
где А0 –
начальная амплитуда. Зависимость
амплитуды показана на рис. 8.3.
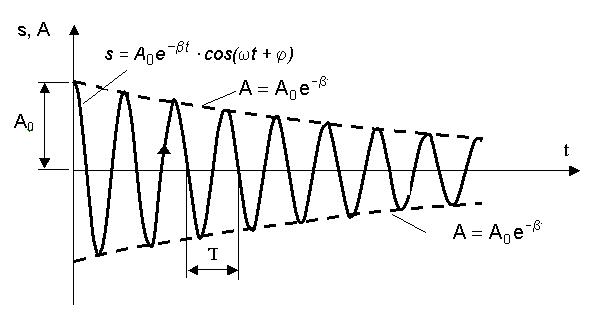
8.3. График затухающих колебаний
-
Механическая
работа (определение, единицы измерения).
Мощность силы (определение, единицы
измерения).
Механическая
рабоат
— то
скалярная физическая величина, которая
характеризует процесс перемещения тела
под действием силы и равна произведению
модуля силы F на модуль перемещения S и
на косинус угла между
ними
Если
тело под действием силы совершает
перемещение ,
работа А этой
силы равна скалярному произведению
силы на вектор перемещения. Работа силы
есть скалярная величинаА=
А=
мощность
силы —
скалярная физическая величина N, равная
отношению работы А, совершаемой силой,
к промежутку времени ,
в течение которого она совершается:

силы, совершаемая в единицу времени,
называется мощностью.
Мощность N это
физическая величина, равная отношению
работы A к
промежутку времени t,
в течение которого совершена эта
работа:
В
Международной системе (СИ) единица
мощности называется ватт
(Вт).
Ватт равен мощности силы, совершающей
работу в 1 Дж за время 1 с.
Если
тело движется прямолинейно и на него
действует постоянная сила, то она
совершает работу .
Поэтому мощность этой силы
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
— амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий — по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.
Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По 3-му закону Ньютона формула силы натяжения записывается как T=mg при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.
Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.
Рисунок 2.4.1. Модель превращения энергии при колебаниях.
Математический и пружинный маятник
Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.
Формулы, характеризующие груз на пружине:
E=Ek+Ep=mυ22+kx22, ω02=km,(Ep)max=kxm22, (Ek)max=mυm22=mω02xm22=(Ep)max.
Выражения при малых колебаниях математического маятника записываются:
E=Ek+Ep=mυ22+mgh=mυ22+mgx22l, ω02=gl,(Ep)max=mghm=mgxm22l, (Ek)max=mυm22=mω02xm22=(Ep)max.
Значение hm является максимальной высотой подъема маятника, xm и υm=ω0xm – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.
Если рассматривать колебания с грузом массой m на пружине с жесткостью k, тогда смещение груза x(t) из положения равновесия и его скорость υ(t) могут изменяться со временем согласно законам:
x(t)=xmcos (ω0t), где ω02=km,
υ(t)=-ωxmsin (ω0t).
Формулы кинетической и потенциальной энергии запишутся так:
Ep(t)=12kx2=12kxm2 cos2ω0t=14kxm2(1+cos 2ω0t),
Ek(t)=12mυ2=12kω02xm2 sin2ω0t=14kxm2(1-cos 2ω0t).
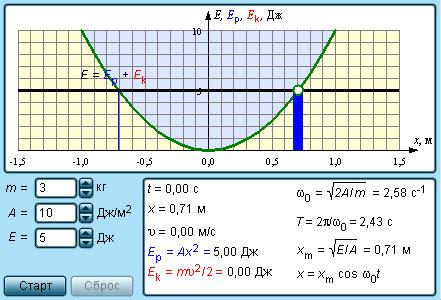
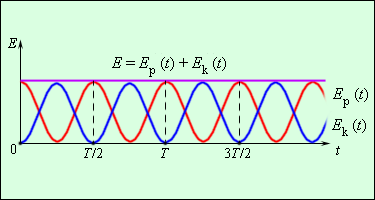
Рисунок 2.4.2 показывает два графика функций изменения Ep(t) и Ek(t). Обе энергии в период колебаний T=2πω0, достигают максимальных значений по два раза. Значение их суммы не изменяется Ep(t)+Ek(t)=E=const.
Рисунок 2.4.2. Превращения энергии при свободных колебаниях.
Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).
При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке 2.4.3.
Рисунок 2.4.3. Свободные затухающие механические колебания.
Скорость затухания колебаний зависит от величины сил трения.
Частота. Добротность. Формулы
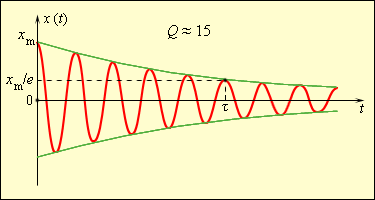
Промежуток времени τ с уменьшением колебаний в e≈2,7 раз называют временем затухания.
Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.
Колебательная система с затухающими колебаниями характеризуется добротностью Q.
Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π:
Q=πN=πτT.
Повышение Q колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке 2.4.3 показано, что Q имеет значение, приближенное к 15.
Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:
Q=2πЗапас энергии в колебательной системеПотеря энергии за 1 период колебаний.
То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.
Частота математического маятника
Виктор Матвеевич Скоков
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Замечание 1
Колебаниям математический маятника — тела с точечной массой, подвешенного на упругой нити — свойственен изохронизм. Это значит, что их частота не зависит от амплитуды и массы подвешенного тела. Такая система обладает свойствами гармонического осциллятора — устройства, график движения тела, в котором представляет собой синусоиду.
Функция, описывающая гармонические колебания:
$varphi (t) = varphi_0 cdot cos(omega_0 + alpha)$, где:
- $ alpha$- начальная фаза колебаний,
- $varphi_0$ — их амплитуда,
- $omega_0$ — циклическая частота.
Циклическая частота связана с длиной подвеса математического маятника зависимостью:
$omega_0 = sqrt{frac{g}{l}}$,
где $g$ — ускорение свободного падения, $l$ — длина нити.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
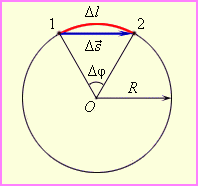
Эта зависимость получается исходя из того, что при малых отклонениях от вертикали касательную (тангенциальную) составляющую силы, тянущей маятник по дуге, можно найти как сумму векторов силы упругости нити (направлена от тела к центру вращения вдоль нити) и силы тяжести (направлена вертикально вниз). Ускорение, создаваемое касательной силой, относится к ускорению свободного падения в следующем соотношении:
$a = g cdot frac{x}{l}$,
где $l$ — длина нити, $x$ — модуль касательной силы.
Поскольку же уравнение колебательного движения выглядит как
$a = — omega_0^2 cdot x$,
где $omega_0$ — частота циклических колебаний, можно подставить в формулу для нахождения периода колебаний полученное соотношение:
$T = frac{2pi}{omega_0}; omega_0 = sqrt{frac{g}{l}} implies T = 2pi cdot sqrt{frac{l}{g}}$
Частоту можно найти как величину, обратную периоду.
$f = frac{1}{T}$
Пример 1
Найти частоту колебаний маятника с длиной подвеса 1 м.
$T = 2 cdot 3,14 cdot sqrt{frac{1}{9,8}} approx 2 с$.
$f = frac{1}{2} = 0,5$
Ответ: 0,5 колебаний в секунду.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 22.04.2023
Похожие материалы по теме
Автор(ы):
Алексей Алексеевич Ивахно
Автор(ы):
Алексей . Малеев
Автор(ы):
Андрей Геннадьевич Блохин
Автор(ы):
Сергей Феликсович Савельев
Автор(ы):
Наталья Николаевна Пушкина
Решение любого учебного вопроса за 300₽