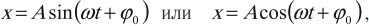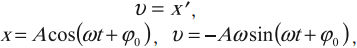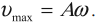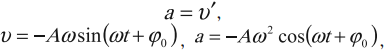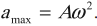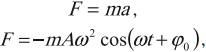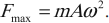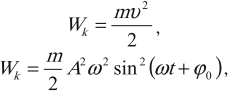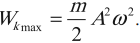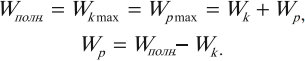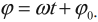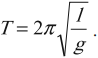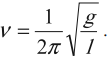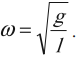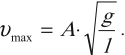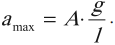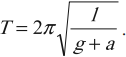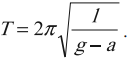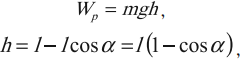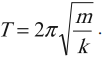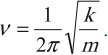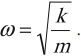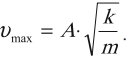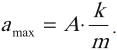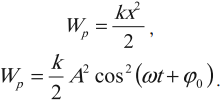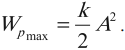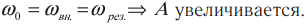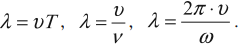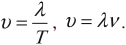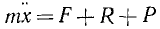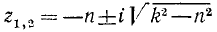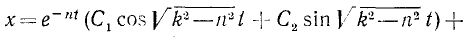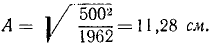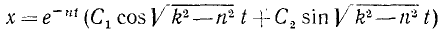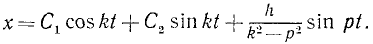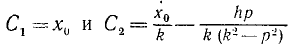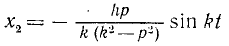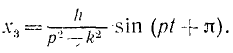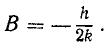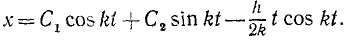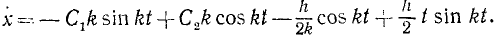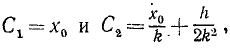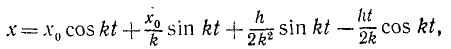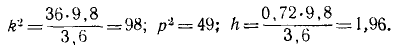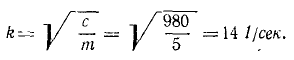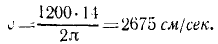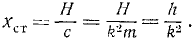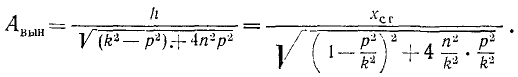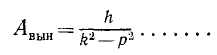Как найти частоту колебаний материальной точки

Содержание:

1. Колебания материальной точки
2. Свободные гармонические колебания материальной точки
3. Влияние постоянной силы на свободные колебания
4. Порядок решения задач на свободные колебания
5. Примеры решения задач на тему: Колебания материальной точки
6. Затухающие колебания материальной точки
7. Примеры решения задач на тему: Затухающие колебания материальной точки
8. Вынужденные колебания материальной точки без учета сопротивления
9. Амплитуда вынужденных колебаний
10. Явление резонанса
11. Примеры решения задач на тему: Вынужденные колебания точки

Прямолинейные колебания материальной точки – колебательное движение материальной точки — движение, происходящее при условии: имеется восстанавливающая сила, стремящаяся вернуть точку в положение равновесия при любом отклонении ее из этого положения. Свободные колебания – происходят под действием только восстанавливающей силы.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Колебания материальной точки

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Свободные гармонические колебания материальной точки

Свободные гармонические колебания материальной точки происходят под действием восстановительной силы, которая пытается вернуть точку в положение равновесия. Примером такой силы может быть сила упругости пружины.

Восстановительная сила меняется по линейному закону. Если на материальную точку действует сила упругости пружины , то:

где  — деформация пружины,

 — коэффициент жесткости.

Коэффициент жесткости многочисленно равен силе, которую необходимо приложить к пружине для того, чтобы деформировать ее на единицу длины.

Единицей измерения коэффициента жесткости в системе единиц Си является .
В практике чаще применяется единица .

Движение материальной точки с массой  по горизонтальной оси (рис.3.1) под действием восстановительной силы , которая равна по модулю , описывается дифференциальным уравнением:

Решение этого уравнения, или закон изменения координаты от времени , выглядит так:

где  и  — постоянные интегрирования, которые определяются по первоначальным условиям.

В амплитудной форме уравнение движения записывается следующим образом:

где  — амплитуда колебаний, то есть наибольшее отклонение колеблющейся точки от положения равновесия;

— фаза колебаний;
 — начальная фаза колебаний;
— круговая частота колебаний, то есть количество колебаний материальной точки за  секунд:

Если исходные условия движения материальной точки при  имеют вид то:

Из приведенных зависимостей вытекает, что амплитуда и начальная фаза  зависят от первоначальных условий, а период и круговая частота — не зависят от первоначальных условий.

Влияние постоянной силы на свободные колебания

В этом случае начало отсчета выбирается в положении статического равновесия, то есть на расстоянии, которое откладывается в направлении постоянной силы и определяется по соотношению:

где — модуль постоянной силы.

Дифференциальное уравнение движения при наличии постоянной силы совпадает по форме с дифференциальным уравнением свободных колебаний. Отсюда выходит, что

Период колебаний и круговая частота равны:

Порядок решения задач на свободные колебания

Решение задач на свободные колебания материальной точки рекомендуется делать в следующем порядке:

1. Изобразить материальную точку в произвольном положении и показать силы, которые на нее действуют.
2. Выбрать систему отсчета, начало координат разместить в положении статического равновесия и направить ось в сторону движения точки.
3. Записать начальные условия движения материальной точки.
4. Составить дифференциальное уравнение движения материальной точки в проекции на соответствующую ось.
5. Проинтегрировать дифференциальное уравнение движения.
6. Определить постоянные интегрирования, используя исходные условия.
7. Записать окончательное уравнение движения.

Примеры решения задач на тему: Колебания материальной точки

Задача № 1

Определить максимальное удлинение  пружины (рис. 3.2, а) в сантиметрах при свободных вертикальных колебаниях груза, если он прикреплен в точке к недеформированной пружине и отпущен из состояния покоя. Статическая деформация пружины под действием груза равняется 

Решение. Изобразим груз в произвольном положении (рис.3.2, б) и покажем силы, которые на него действуют: силу упругости пружины , которая является восстановительной силой, и силу тяжести груза .

Поскольку на груз помимо восстановительной силы , действует и постоянная сила — сила тяжести груза , то центр колебаний сместим относительно конца недеформированной пружины в направлении силы тяжести на (точка ). Ось направим в направлении движения груза.

Когда груз будет находиться в крайнем нижнем положении (рис.3.2, б), то максимальное удлинение пружины будет состоять из статической деформации и амплитуды свободных колебаний:

Величину амплитуды можно определить из выражения:

где  — исходное положение груза;

 – начальная скорость груза.

По условию задачи при

Подставляя значения  и  в уравнение (1), достанем:

Таким образом, максимальное удлинение пружины равно:

Ответ:

Задача № 2

Груз массой подвешен к пружине с коэффициентом жесткости  и находится в свободном прямолинейном колебательном движении.

Определить модуль ускорения  груза в момент времени, когда его центр тяжести находится на расстоянии 5 см от положения статического равновесия.

Решение. При изучении свободных колебаний под действием восстановительной (сила упругости пружины) и постоянной силы (в данном случае — силы тяжести ) начало координат лучше всего выбрать в положении статического равновесия (точка ) (рис.3.3), то есть смещенным на относительно недеформированного состояния в направлении силы . Тогда уравнение движения груза будет иметь вид:

Для нахождения ускорения груза два раза продифференцируем это уравнение по времени:

Последнее выражение представим в виде:

поскольку

Определим круговую частоту колебаний, которая входит в правую часть уравнения (2):

По условиям задачи необходимо определить модуль ускорения груза, когда его центр тяжести находится на расстоянии 5 см от положения статического равновесия, то есть

Окончательно:

Ответ: 

Задача № 3

Определить эквивалентный коэффициент жесткости двух пружин и период колебаний груза весом , подвешенного к этим пружинам, если пружины соединены последовательно (рис. 3.4,а) и параллельно (рис. 3.5). Коэффициенты жесткости пружин:

Решение: в случае последовательного соединения пружин общее статическое удлинение будет равняться сумме статических удлинений первой и второй пружины:

Поскольку каждая из пружин в статическом положении растягивается силой , то согласно (3.7):

С учетом последних соотношений формула (1) примет вид:

Для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

где  — коэффициент жесткости эквивалентной пружины, заменяющей две последовательно соединенные пружины.

Поскольку статическое удлинение заданной (рис. 3.4,а) и эквивалентной (рис. 3.4,б) схем должно быть равным, то:

С учетом числовых данных:

Период колебаний по формуле (3.8):

В случае параллельного соединения пружин (рис. 3.5) их статическое удлинение будет одинаковым:

Исходя из формулы (3.7) пружины будут растянуты усилиями:

Таким образом, сила тяжести груза будет уравновешиваться двумя вертикальными усилиями  и  пружин, то есть, 

или

С другой стороны, для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

де  — коэффициент жесткости эквивалентной пружины, заменяющей две параллельные пружины.

Отсюда

С учетом числовых данных:

Период колебаний по формуле (3.8):

Ответ: 

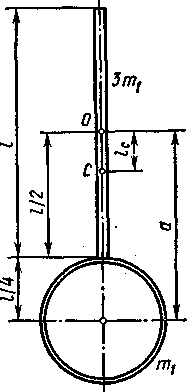
Задача № 4

Пружина , которая закреплена одним концом в точке , является такой, что для удлинения ее на необходимо приложить в точке при статической нагрузке силу . В некоторый момент времени к нижнему концу недеформированной пружины подвешивают гирю , массой  и отпускают ее без начальной скорости. Пренебрегая массой пружины, написать уравнение дальнейшего движения гири и определить амплитуду и период ее колебаний, относя движение гири к оси, которая проведена вниз из положения статического равновесия гири.

Определить:

Решение. Изобразим гирю в промежуточном положении (рис.3.6). На нее действуют сила тяжести и сила упругости . Ось направим вертикально вниз, а начало отсчета
возьмем в точке , которая отдалена от конца  недеформированной пружины на величину .

Начальные условия при имеют вид:

Уравнение движения гири запишем в дифференциальной форме:

С другой стороны

Тогда

Статическое отклонение равно:

 или 

Подставив в (1) выражение для , получим:

Решение этого дифференциального уравнения в амплитудной форме имеет вид:

Круговая частота колебаний гири определяется зависимостью (3.4):

где 

Тогда 

Определим амплитуду колебаний гири по формуле (3.5):

где 

Тогда,

а поскольку

то амплитуда колебаний гири

Начальную фазу колебаний найдем по формуле (3.5):

С учетом найденных величин , и уравнение (1) движения гири имеет вид:

Период свободных колебаний гири равен (3.8):

Ответ: 

Задача № 5

Во время равномерного опускания груза весом со скоростью , от зажатия троса в обойме блока (рис.3.7), случилась внезапная задержка верхнего конца троса, на котором опускался груз.

Определить наибольшее натяжение троса во время колебания груза, если коэффициент жесткости троса . Весом троса пренебречь.

Решение. Начало координат выбираем в положении статического равновесия на расстоянии от начального состояния (точка ).

Из условия задачи вытекает, что максимальное натяжение троса будет при крайнем нижнем положении груза . В этом случае деформация будет равна сумме статического отклонения и амплитуды колебаний груза . Таким образом:

Итак, задача сводится к определению амплитуды колебаний.

Амплитуда колебаний определяется с помощью начальных условий:

где  — исходное положение груза ;

 — начальная скорость груза Q .

В данной задаче начальные условия при имеют вид:

Определяем круговую частоту колебаний:

и величину статического отклонения:

Тогда

Максимальное натяжение троса равно:

Надо обратить внимание на то, что груз весом при зажатии троса вызывает в нем усилие в 23 раза больше, чем его вес, что может привести к разрыву троса и аварии.

Ответ: 

Задача № 6

Груз , падающий с высоты без начальной скорости, бьется о середину упругой горизонтальной балки, концы которой  и  закреплены (рис.3.8).

Определить уравнение последующего движения груза вместе с балкой относительно оси, которая проведена вертикально вниз из положения статического равновесия балки вместе с грузом. При статической нагрузке балки в средней ее части силой, равной силе тяжести груза , прогиб составляет Массой балки пренебречь.

Решение. Изобразим груз в промежуточном положении. На груз действует: сила тяжести и сила упругости балки . Ось направим вниз, начало отсчета берем в точке , которая находится на расстоянии от горизонтального положения балки.

Запишем начальные условия движения.

Координата  груза в начале колебательного движения равна . Скорость средней точки балки, которая колеблется вместе с грузом, в начале движения будет равна скорости груза при его падении с высоты :

Таким образом, при :

Если начало отсчета совпадает с положением статического равновесия, то уравнение движения имеет вид:

Для определения постоянных интегрирования  и  нам кроме закона движения надо иметь и закон изменения скорости:

Для определения круговой частоты колебаний найдем коэффициент жесткости балки.

Поскольку  то 

Тогда 

Из начальных условий (при ) и закона движения (1) находим постоянную интегрирования :

Из уравнения (2) и начальных условий (при :  ) находим постоянную интегрирования :

Окончательно, уравнение движения груза примет вид

Ответ: 

Задача № 7

В клапанном механизме (рис. 3.9,а) закон движения толкателя 2 задается профилем кулачка 1 и передается на клапан 3. На клапане 3 установлена пружина 4, которая обеспечивает постоянный контакт между рабочими поверхностями кулачка 1 и толкателя 2. При проектировании быстроходных кулачковых механизмов приходится учитывать характеристики реальных деталей, которые отличаются от характеристик абсолютно твердых тел. Например, низкая жесткость, значительные массы и большие ускорения при движении деталей газораспределительных механизмов двигателей внутреннего сгорания приводят к возникновению упругих колебаний, которые накладываются на заданное движение деталей.

Считается, что податливость имеют кулачок 1, толкатель 2 и клапан 3 с пружиной 4. При создании динамической модели механизма, которая отражает влияние упругости деталей реального механизма, используют одномассовую модель (рис. 3.9, б). Масса учитывает массы кулачка, толкателя и клапана, пружина с коэффициентом жесткости клапанную пружину 4, а пружина  коэффициентом жесткости жесткость кулачка, толкателя и клапана.

Определить коэффициент жесткости и частоту колебаний деталей такого механизма, если: коэффициент жесткости клапанной пружины и статическую нагрузку величиной вызывает деформацию Силами трения в направляющих толкателя и клапана пренебречь.

Решение. При статической нагрузке на тело массой (рис. 3.9) действуют три силы: статическая нагрузка и силы упругости пружин и .

Сила упругости пружины , длина которой в недеформированном состоянии , пропорциональна статическому удлинению :

и направлена вверх, поскольку пружина сжата.

Сила упругости пружины , длина которой в недеформированном состоянии , пропорциональна статическому удлинению :

и направлена вверх, поскольку пружина растянута.

Спроектировав эти силы , и  на ось , получим:

или

Исходя из условия совместимости деформации системы имеем:

Тогда

Из уравнения (1) определяем коэффициент жесткости пружины :

Для эквивалентной расчетной схемы с одной пружиной (рис. 3.4, б):

где  — коэффициент жесткости эквивалентной пружины.

Приравняв уравнения (1) и (2) получим коэффициент жесткости эквивалентной пружины:

Круговая частота колебаний (3.4):

Ответ: 

Задачи, которые рекомендуются для самостоятельной работы: 32.11; 32.15; 32.24 [2].

Затухающие колебания материальной точки

Материальная точка, которая колеблется при реальных условиях, испытывает сопротивление движению (силы трения, сопротивление воздуха и т.п.). Это значит, что помимо восстановительной силы, которая направлена к центру колебаний, действует сила сопротивления, которая направлена всегда в сторону, противоположную направлению движения точки.

Рассмотрим колебания материальной точки (рис.3.10) под действием восстановительной силы и силы сопротивления , которая пропорциональна модулю скорости точки .

Векторное уравнение движения точки в этом случае имеет вид:

В проекции на ось :

поскольку , где  — коэффициент сопротивления среды.

После преобразований, уравнение (3.11) примет вид:

Если обозначить:  то 

Уравнение (3.12) является дифференциальным уравнением движения материальной точки под действием восстанавливающей силы и силы сопротивления, пропорциональной скорости точки.

Решение уравнения (3.12) имеет разный вид в зависимости от соотношения коэффициентов и .

а) Случай малого сопротивления

В этом случае решение уравнения (3.12) имеет вид:

Движение, которое соответствует уравнению (3.13), имеет колебательный характер, потому что координата периодически меняет свой знак, что зависит от знака синуса, который входит в уравнение. Множитель  показывает на то, что амплитуда колебаний с течением времени уменьшается. Колебания такого вида называются затухающими.

В уравнении (3.13):

,  — постоянные интегрирования (определяются по начальным условиям);

 — коэффициент затухания;

 — частота затухающих колебаний, 

График затухающих колебаний показан на рис.3.11.

Поскольку:

то координата затухающих колебаний размещается между двумя симметричными относительно оси абсцисс кривыми, которые соответствуют уравнению

Промежуток  времени, который равен

называется периодом затухающих колебаний, то есть, это есть время, за которое точка совершает полное колебание.

Выражение (3.14) можно представить в виде:

где  — период свободных колебаний.

Амплитудой затухающих колебаний называют наибольшее отклонение точки в ту или иную сторону от положения равновесия.

На рис.3.11 показаны амплитуда  и  в промежуток половины одного периода:

Отношение следующей амплитуды к предыдущей представляет собой знаменатель геометрической прогрессии, который не изменяется во время всего колебательного процесса, и называется декрементом колебаний.

Модуль натурального логарифма декремента колебаний называется логарифмическим декрементом.

б) Предельный случай

В этом случае уравнение движения точки имеет вид

Движение точки, которое соответствует уравнению (3.18), называется апериодическим и не является колебательным. Точка из любого положения приближается к положению . График этого движения приведен на рисунке 3.12.

в) Случай большого сопротивления

Решение дифференциального уравнения (3.12) в этом случае имеет вид:

где

Поскольку функции  и  с течением времени монотонно уменьшаются, приближаясь к нулю, то движение точки в этом случае не будет колебательным и она под действием восстанавливающей силы будет постепенно приближаться к положению равновесия. Движение также будет апериодическим.

В зависимости от начальных условий материальная точка может совершать одно из апериодических движений, графики которых показаны на рис. 3.13.

Рис. 3.13, а характеризует движение точки с начальной скоростью , совпадающей с положительным направлением оси . Сначала точка отдаляется от положения равновесия, а затем под действием восстановительной силы постепенно приближается к этому положению.

Графики, приведенные на рис. 3.13,б и рис 3.13,в, соответствуют движению точки с начальной скоростью , которая направлена противоположно положительному направлению оси . При достаточно большой начальной скорости точка может совершить переход через положение равновесия и после этого при обратном движении приблизиться к этому положению (рис 3.13,б).

Примеры решения задач на тему: Затухающие колебания материальной точки

Решение задач на затухающие колебания состоит из 2-х частей. В первой части основное внимание отводится ознакомлению с важнейшими понятиями и характеристиками затухающего колебательного процесса. Вторая часть занятия посвящена составлению и решению уравнений затухающих колебаний.

Задача №8

Дифференциальное уравнение движения материальной точки имеет вид

Определить максимальное значение массы точки, при котором движение будет апериодическим.

Решение. Движение точки будет апериодическим, если выполняется условие:

где  — коэффициент сопротивления,

 — частота свободных незатухающих колебаний.

Заданное дифференциальное уравнение приведем к каноническому виду, разделив на массу:

Отсюда:

С учетом полученных значений и , условие (1) примет вид:

Решаем неравенство (2) относительно массы :

Ответ: максимальное значение массы 

Задача №9

Дифференциальное уравнение движения материальной точки имеет вид: , где в см .

Определить максимальное значение коэффициента жесткости , при котором движение будет апериодическим.

Решение. Движение точки будет апериодическим, если выполняется условие:

Исходное дифференциальное уравнение движения материальной точки приводим к виду:

Тогда: 

Таким образом, условие (1) имеет вид:

Откуда

 и 

Ответ: максимальное значение коэффициента жесткости 

Задача № 10

Тело весом , что подвешенное на пружине, которую сила растягивает на , при движении встречает сопротивление, величина которого пропорциональна первой степени скорости. Сила сопротивления при скорости равна . В начальный момент пружина была растянута относительно положения равновесия на , и тело начало двигаться без начальной скорости, то есть, .

Определить уравнение движения тела .

Решение. Перед тем, как записать общее уравнение движения точки, необходимо выяснить, при каком сопротивлении происходит движение, то есть сравнить значения коэффициента и круговой частоты :

Из условия задачи вытекает:

Таким образом, , то есть коэффициент сопротивления равен круговой частоте, и движение точки будет апериодическим.

В этом случае закон движения точки определяется зависимостью (3.18):

Начальные условия: 

Подставляя их в уравнение (1), получим:

Ответ: 

Найдя по формуле (2) значение в зависимости от времени (табл. 3.1), построим график (рис.3.14).

Таблица 3.1

	0	0,2	0,4	0,6	0,8	1,0
	5	3,68	2,0	0,99	0,46	0,2

Из графика видно, что при точка не колеблется и быстро приближается к положению равновесия () . Выясним теперь, переходит ли груз положения статического равновесия. Для этого приравняем  в уравнении (2) к нулю:

Моменты времени, в которые груз находится в положении статического равновесия определяются из уравнений:

 и 

Из первого уравнения вытекает: 

Из второго уравнения: 

Значение соответствует угасанию движения, отрицательное значение показывает на отсутствие перехода тела через положение статического равновесия.

Задача № 11

Грузы весом и подвешены (рис.3.15, а) в положении статического равновесия к пружине 1, коэффициент жесткости которой , и масляного демпфера 2, которая влечет пропорциональную первой степени скорости силу сопротивления, равную , где . Груз  вдруг сняли.

Определить уравнение движения груза после снятия груза .

Решение. Изобразим расчетную схему для движения груза (рис.3.15, б).

На схеме обозначено:

— длина недеформированной пружины;

– деформация пружины под действием силы тяжести груза ;

 — деформация пружины под действием силы тяжести груза .

– деформация пружины под действием сил тяжести грузов и .

Ось колебаний направим вниз (ось ). Начало отсчета возьмем в точке , в положении статического равновесия пружины под действием силы тяжести груза , поскольку во время движения груз отсутствует.

Исходя из принятой схемы, исходные условия будут:

исходное положение груза :

начальная скорость груза :

Для определения вида движения груза необходимо сравнить значения коэффициента затухания и круговой частоты свободных колебаний .

где  — масса груза ;

 — коэффициент жесткости пружины;

 — коэффициент сопротивления среды.

После подстановки числовых данных получим:

Итак, 

Таким образом, в задаче рассматривается случай большого сопротивления () и уравнение движения груза имеет вид (3.20):

где  и  – постоянные интегрирования, которые определяются по начальным условиям.

Подсчитаем величину коэффициента :

С учетом того, что  уравнение (1) примет вид:

Для определения постоянных интегрирования  и  выразим зависимость скорости груза  от времени:

Подставим в уравнение (2)  а в уравнение (3) 

Получим: 

Из уравнений (2′) и (3′) находим:

Окончательно, уравнение движения груза имеет вид:

Как и в предыдущей задаче, построим график изменения координаты (табл. 3.2) в зависимости от времени (рис.3.16).

Таблица 3.2

	0	0,2	0,4	0,6	0,8	1,0
	7,5	3,45	1,43	0,59	0,25	0,1

Ответ: 

Задача № 12

Тело весом , которое подвешено к пружине, при отсутствии силы сопротивления колеблется с периодом а если действует сила сопротивления, пропорциональная скорости, то с периодом

Определить силу сопротивления  при скорости и определить уравнение движения , если в начальный момент пружина была растянута из положения статического равновесия на

Решение. Если скорость тела то сила сопротивления численно будет равна коэффициенту силы сопротивления, поскольку

Коэффициент пропорциональности связан с коэффициентом затухания зависимостью:

Итак, для определения  необходимо найти значение коэффициента затухания , который можно определить из выражения:

где  — частота свободных колебаний при отсутствии сопротивления,

 — частота затухающих колебаний.

Поскольку

то

 и 

и

Следовательно, сила сопротивления при скорости движения равна:

Переходим к определению закона движения тела. Составим расчетную схему (рис.3.17).

На схеме

 — длина недеформированной пружины,

 — статическое удлинение пружины под действием силы тяжести тела,

 — переменная координата положения тела,

 — исходное положение тела.

Ось колебаний направляется вниз (ось ), а начало координат (точка ) выбирается в положении статического равновесия.

Поскольку (случай малого сопротивления), то закон движения тела под действием силы тяжести , восстанавливающей силы и силы сопротивления выражается уравнением:

Учитывая, что  то:

Для определения постоянных интегрирования и , кроме уравнения (2), запишем уравнение зависимости скорости от времени:

В уравнения (2) и (3) подставим начальные условия:

при , 

Из уравнения (3′) определяем постоянную :

Из уравнения (2′) находим постоянную :

С учетом полученных значений , уравнение движения тела будет:

Построим график зависимости (рис.3.18)

Таблица 3.3

Задача № 13

Материальная точка совершает прямолинейные колебания под действием восстанавливающей силы, модуль которой пропорционален расстоянию от точки к некоторому неподвижному центру , и силы сопротивления среды, модуль которой пропорционален скорости точки. В начальный момент времени смещение точки и ее скорость

Определить закон движения точки, если период колебаний равен , а декремент колебаний — 

Решение. Выберем начало координат в неподвижном центре , а ось направим вдоль прямолинейной траектории точки . Покажем силы, действующие на материальную точку (рис.3.19):

 — восстановительная сила, модуль которой пропорционален отклонению точки от положения равновесия , где  — коэффициент жесткости;

– сила сопротивления среды, модуль которой пропорционален скорости точки , где – коэффициент сопротивления среды.

Дифференциальное уравнение движения точки массой  будет иметь следующий вид:

или

Сведем записанное уравнение к виду:

или

где

Мы получили дифференциальное уравнение (3.12) затухающих колебаний.

Решение дифференциального уравнения (1) будет иметь вид:

Чтобы найти коэффициенты и воспользуемся формулами (3.14) и (3.16):

Из первой из этих формул найдем :

Из второй формулы найдем :

С учетом найденных значений и уравнение (2) примет вид:

Учитывая, что

то уравнение движения точки будет иметь вид:

Постоянные  и определим из начальных условий. При начальная скорость и начальная координата

После предварительного дифференцирования уравнения (2) по времени :

Поскольку при , то:

Из уравнения (4) определим постоянную . Поскольку , то , то есть .

Из уравнения (5) после подстановки найдем :

С учетом найденных значений и , уравнение (2) движения точки примет вид:

Ответ: 

Задачи, которые рекомендуются для самостоятельной работы: 32.55; 32.58; 32.59; 32.64 [2]

Вынужденные колебания материальной точки без учета сопротивления

Вынужденные колебания совершает материальная точка (рис.3.20), на которую вместе с восстановительной силой действует возбуждающая сила , периодически изменяющаяся.

Пусть проекция возбуждающей силы на ось, которая совпадает с направлением движения точки меняется по закону:

где  — максимальное значение возбуждающей силы;

 — частота изменения возбуждающей силы;

 — фаза изменения возбуждающей силы;

 — начальная фаза изменения возбуждающей силы.

Дифференциальное уравнение движения точки в проекции на ось имеет вид:

или

Если обозначить

то получим дифференциальное уравнение вынужденных колебаний материальной точки:

Решение уравнения (3.22) в амплитудной форме, то есть, зависимость координаты от времени , имеет вид:

где  — амплитуда вынужденных колебаний имеет вид:

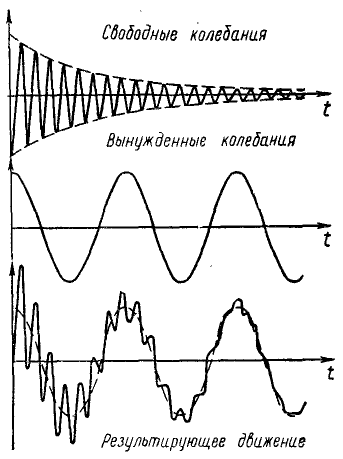
Из уравнения (3.22) вытекает, что движение точки представляет собой наложение двух колебательных движений.

Колебания, определяемые первым слагаемым:

имеют частоту свободных гармонических колебаний и называются собственными колебаниями материальной точки.

Колебания, определяемые вторым слагаемым

имеют частоту возбуждающей силы и называются вынужденными колебаниями материальной точки.

Таким образом, при одновременном действии восстанавливающей и возбуждающей сил точка совершает сложное колебательное движение, которое представляет собой результат наложения свободных и вынужденных колебаний точки.

Из уравнения (3.24) вытекает, что вынужденные колебания не зависят от начальных условий.

Необходимо подчеркнуть, что частота и период  вынужденных колебаний являются также частотой и периодом возбуждающей силы.

Вынужденные колебания, частота которых меньше частоты свободных колебаний точки, называют вынужденными колебаниями малой частоты.

Вынужденные колебания, частота которых больше частоты свободных колебаний, называют вынужденными колебаниями большой частоты.

Фаза вынужденных колебаний

Если (случай вынужденных колебаний малой частоты), то , и фаза вынужденных колебаний совпадает с частотой возбуждающей силы. В этом случае:

Если вынужденные колебания происходят с большой частотой то и для того, чтобы амплитуда колебаний была положительной, ее записывают в виде:

При этом, фаза вынужденных колебаний большой частоты равна и отличается от фазы возбуждающей силы  на величину , то есть фазы возбуждающей силы и вынужденных колебаний противоположны.

В случае вынужденных колебаний малой частоты точка всегда отклонена от начала координат в ту сторону, в которую направлена в данный момент возбуждающая сила .

В случае вынужденных колебаний большой частоты отклонение точки от начала координат всегда противоположное направлению возбуждающая сила . При этом в обоих случаях максимальное отклонение точки от начала координат происходит в тот момент времени, когда модуль возбуждающей силы достигает максимума.

Амплитуда вынужденных колебаний

Статическим отклонением точки называется величина  (рис.3.21), которая определяется из условия:

Отсюда 

где  — максимальное значение возбуждающей силы.

Отношение амплитуды вынужденных колебаний к статическому отклонению называется коэффициентом динамичности.

При 

При 

График изменения коэффициента динамичности в зависимости от изменения частоты возбуждающей силы (рис.3.22) имеет разрыв при значении  В этом случае коэффициент динамичности увеличивается к бесконечности и наступает так называемое явление резонанса.

Явление резонанса

Явление резонанса возникает когда частоты вынужденных и свободных колебаний точки совпадают, то есть:

При этом амплитуда вынужденных колебаний точки равна бесконечности и большинство уравнений вынужденных колебаний, полученных при условии , теряют смысл.

Дифференциальное уравнение движения при , примет вид:

Уравнение (3.28) отличается от уравнения (3.22) тем, что в правой части стоит частота , которая равна частоте собственных колебаний точки.

Решение дифференциального уравнения (3.28) имеет вид:

При резонансе частота и период вынужденных колебаний равны, соответственно, частоте и периоду свободных колебаний точки, а фаза вынужденных колебаний  отстает от фазы возбуждающей силы на величину

Графиком отклонений для вынужденных колебаний во время резонанса является периодическая кривая, напоминающая синусоиду (рис.3.23), что вписывается в область, ограниченную прямыми  и  поскольку не больше единицы. При точки графика лежат на этих прямых.

Из графика видно, что амплитуды колебаний увеличиваются со временем.

Примеры решения задач на тему: Вынужденные колебания точки

Задачи на вынужденные колебания точки рекомендуется решать в следующей последовательности:

1. Выбрать систему координат, взяв за начало положение статического равновесия точки;

2. Записать начальные условия движения точки;

3. Изобразить на рисунке силы, приложенные к точке;

4. Составить дифференциальное уравнение движения в проекции на соответствующую ось;

5. Проинтегрировать дифференциальное уравнение движения, использовав начальные условия для определения постоянных интегрирования, определить искомые величины.

При решении задачи материальную точку рекомендуется изображать в промежуточном положении, где ее координата на оси будет положительной.

Если составленное дифференциальное уравнение движения точки тождественно с одним из выше записанных уравнений, то не интегрируя это уравнение, можно сразу получить решение по приведенным формулам.

Задача № 14

На тело, которое подвешено к пружине, действует вертикальная возбуждающая сила

Определить коэффициент динамичности, если круговая частота свободных колебаний тела

Решение. Сравнивая заданное в условиях значение для возбуждающей силы с выражением (3.21):

получим, что частота ее изменения

Поскольку , то в данной задаче имеем вынужденные колебания малой частоты.

Коэффициент динамичности в этом случае соответственно с (3.26) равен:

Ответ: 

Задача № 15

Дифференциальное уравнение колебательного движения материальной точки имеет вид:

Определить коэффициент динамичности .

Решение. Сравнивая заданное в условиях задачи уравнение колебательного движения с (3.22):

получим: 

Поскольку , то имеем вынужденные колебания малой частоты и коэффициент динамичности равен:

Ответ:  

Задача № 16

Статическое удлинение пружины

Определить коэффициент динамичности, если на груз действует вертикальная возбуждающая сила

Решение. Сравнивая заданное в условиях задачи выражение для возбуждающей силы с (3.21):

получим: 

Для определения коэффициента динамичности необходимо найти частоту собственных колебаний .

Учитывая, что

а статическое удлинение пружины

то

 или 

Поскольку то из (3.26) получим:

Ответ:  

Задача №17

Материальная точка массой  совершает прямолинейные колебания вдоль оси (рис.3.24) под действием возбуждающей силы и восстановительной силы , модуль которой пропорционален расстоянию точки от начала координат (коэффициент пропорциональности равен ).

Определить закон движения точки, если в начальный момент и

Решение. Дифференциальное уравнение движения материальной точки в данном случае имеет вид:

или

Уравнение (1) является дифференциальным уравнением вынужденных колебаний (3.22), в котором:  (то есть );  и 

Поскольку , то общее решение уравнения (1) находим из формулы (3.23):

В нашем случае это уравнение будет иметь вид:

или

Учитывая, что , то 

Окончательно,

Перейдем к нахождению постоянных и α. Для этого продифференцируем уравнение (2) по времени :

Подставим в уравнение (2) и (3) начальные условия: при 

Тогда

или

Из второго уравнения находим постоянную . Поскольку , то нулю равен , то есть 

Из первого уравнения находим постоянную :

Таким образом, искомый закон движения точки будет иметь вид:

Ответ: 

Задача № 18

Точка массой движется прямолинейно и притягивается к неподвижному центру силой, которая пропорциональна расстоянию точки к этому центру, причем коэффициент пропорциональности равен  Кроме того, на точку действует возбуждающая сила , которая выражена в Ньютонах (рис.3.24).

Определить закон движения точки , если в начальный момент и

Решение. Составим дифференциальное уравнение движения материальной точки , выбрав при этом начало координат в центре и направив ось (рис.3.24) вдоль траектории точки:

Получим дифференциальное уравнение в виде (3.22), в котором:

Поскольку частота свободных колебаний и частота вынужденных колебаний совпадают, то имеет место явление резонанса. Закон движения точки определим из формулы (3.29):

В нашем случае эта формула приобретет вид:

Постоянные и найдем из начальных условий. Продифференцировав уравнение (2) по времени , получим:

Подставим в уравнение (2) и (3) начальные условия: при 

Тогда:

или

Из первого уравнения находим постоянную . Поскольку , то нулю равно , то есть

Из второго уравнения находим постоянную :

Таким образом, закон движения точки будет иметь вид:

Ответ: 

Задача № 19

К вертикальной пружине, верхний конец которой закреплен, подвешен груз весом , который придает статическое удлинение пружине . На груз действует вертикальная возбуждающая сила  При пружина была растянута на и грузу предоставлена вниз скорость

Определить закон движения груза 

Решение. Изобразим схему движения груза (рис.3.25).

Вертикаль, по которой движется груз, принимаем за ось , положительным выбираем направление вниз. Начало координат совпадает с положением статического равновесия груза (точка ). В начальный момент времени тело находилось в точке , то есть на расстоянии от конца недеформированной пружины.

Начальные условия для точки (при  ) будут иметь следующий вид:

Для определения закона движения груза необходимо сравнить значения частоты собственных колебаний  и частоты возбуждающей силы .

Из уравнения возбуждающего силы вытекает, что 

Вычислим значение частоты собственных колебаний , исходя из того, что 

Поскольку  а то 

Тогда

Следовательно, , то есть имеет место резонанс, и уравнение движения тела записывается в виде:

где

Следовательно,

или

Для определения постоянных интегрирования и необходимо иметь два уравнения. Одно уравнение получено — это зависимость (2) координаты точки от времени .

Второе уравнение получим, продифференцировав уравнение (2) по времени:

или

Подставим в уравнение (2) и (3) начальные условия: при 

После упрощений:

Решая эти уравнения, находим:

Таким образом, закон движения груза имеет вид:

Построим график (рис.3.26) по уравнению (4) в соответствии с координатами и , которые приводятся в таблице.

Ответ: 

Задача № 20

Определить, какова должна быть величина статического прогиба рессор железнодорожного вагона, чтобы при скорости к  вагон не попал в резонанс с толчками на стыках колеи, расстояние между которыми

Решение. Резонанс наступает тогда, когда период свободных колебаний вагона совпадает с периодом возбуждающего силы, которой будут толчки на стыках рельсов.

Период собственных колебаний вагона равен

Найдем круговую частоту свободных колебаний:

Следовательно, период собственных колебаний равен:

где 

Вычислим период возбуждающей силы, который равен времени прохождения вагоном длины рейки :

Определим , при котором будет явление резонанса, то есть когда :

 или 

Откуда

Таким образом, для избежания резонанса вагона необходимо, чтобы выполнялась неровность:

Ответ: 

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Центр масс
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы

• Уравнение
гармонических колебаний

где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.

• Угловая частота
колебаний

, или
,

где ν
и
Т — частота и период колебаний.

• Скорость точки,
совершающей гармонические колебания,

• Ускорение при
гармоническом колебании

• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле

где
a₁
и
А₂—
амплитуды
составляющих колебаний; φ₁
и
φ₂—
их
начальные фазы.

•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы

•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по зна­чению
частотами ν₁
и
ν₂,

•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A₁
и A₂
и начальны­ми
фазами φ₁
и φ₂,

Если
начальные фазы φ₁
и
φ₂
составляющих колебаний одинако­вы,
то уравнение траектории принимает вид

т. е. точка движется
по прямой.

В том
случае, если разность фаз
,
уравнение
принимает вид

т. е. точка движется
по эллипсу.

• Дифференциальное
уравнение гармонических колебаний
ма­териальной точки

, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω²).

•
Полная энергия
материальной точки, совершающей
гармони­ческие
колебания,

• Период
колебаний тела, подвешенного на пружине
(пружин­ный
маятник),

где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в ко­торых
выполняется закон Гука (при малой массе
пружины в срав­нении
с массой тела).

Период колебаний
математического маятника

где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника

где J
— момент инерции колеблющегося тела
относительно оси

колебаний;
а
— расстояние центра масс маятника от
оси колебаний;

— приведенная
длина физического маятника.

Приведенные
формулы являются точными для случая
бесконеч­но малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.

Период
крутильных колебаний тела, подвешенного
на упругой нити,

где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.

• Дифференциальное
уравнение затухающих колебаний

, или
,

где r
— коэффициент сопротивления; δ
— коэффициент
затухания:

; ω₀—
собственная угловая частота колебаний
*

• Уравнение
затухающих колебаний

где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.

• Угловая частота
затухающих колебаний

О Зависимость
амплитуды затухающих колебаний от
времени

I

где
А₀
— амплитуда
колебаний в момент t=0.

• Логарифмический
декремент колебаний

где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колеба­ний,
отстоящих по времени друг от друга на
период.

• Дифференциальное
уравнение вынужденных колебаний

, или

,

где

—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F₀
—
ее
амплитудное значение;

•
Амплитуда вынужденных
колебаний

•
Резонансная частота
и резонансная амплитуда

и

Примеры решения
задач

Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если

x(0)= см
и х^,(0)<0.
Построить векторную диаграмму для
мо-­
мента t=0.

Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:

Отсюда
найдем начальную фазу:

*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).

Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента

удовлетворяют
два
значения угла:

Для
того чтобы решить, какое из этих значений
угла φ
удовлет-­
воряет
еще и условию
,
найдем сначала
:

Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем

Так
как всегда A>0
и ω>0,
то условию удовлетворяет
толь­
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза

По
найденному значению φ
постро-­
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-­
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-­
ределить: 1) скорость υ
точки
в мо-­
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
F_max,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ­
ки.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

а
формулу скорости получим, взяв первую
производную по времени от смещения:

(2)

Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квад­рат,
разделим первое на А²,
второе
на A²
ω
²
и сложим:

, или

Решив
последнее уравнение относительно υ,
найдем

Выполнив вычисления
по этой формуле, получим

см/с.

Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — ког­да
направление скорости совпадает с
отрицательным направлением оси
х.

Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением

Повторив
с этим уравнением такое же решение,
получим тот же ответ.

2.
Силу действующую на точку, найдем по
второму закону Нью­тона:

(3)

где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:

, или

Подставив выражение
ускорения в формулу (3), получим

Отсюда максимальное
значение силы

Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем

3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента вре­мени.

Проще
всего вычислить полную энергию в момент,
когда кинети­ческая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии

T_max:

(4)

Максимальную
скорость определим из формулы (2),
положив

:
.
Подставив выражение скорости в фор­-
мулу
(4), найдем

Подставив
значения величин в эту формулу и произведя
вычис­ления, получим

или

мкДж.

Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m₃=400
г
укреплены шарики малых размеров массами
m₁=200
г
и
m₂=300г.
Стержень
колеблется около горизонтальной оси,
перпен-

дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.

Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_С
— расстояние
от центра масс ма­ятника
до оси.

Момент
инерции данного маятника равен сумме
моментов
инерции шариков J₁
и
J₂
и
стержня J₃:

(2)

Принимая
шарики за материальные точки, вы­разим
моменты их инерции:

Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J₃=
= .
Подставив
полученные выражения
J₁
,
J₂
и

J₃
в формулу (2), найдем общий момент инерции
фи-­
зического маятника:

Произведя
вычисления по этой формуле, найдем

Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:

Расстояние
l_С
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое рас­стояние
l
равно координате центра масс маятника,
т. е.

, или

Подставив
значения величин m₁,
m₂,
m,
l
и произведя вычисле­ния,
найдем

см.

Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:

Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т₁
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т₁.
Горизонтальная
ось Oz

маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.

Решение.
Период
колебаний физического маятника
опреде­ляется
по формуле

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_C
— расстояние
от центра масс
маятника до оси колебаний.

Момент
инерции маятника равен сумме мо­ментов
инерции стержня J₁
и
обруча J₂:

(2).

Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-­
ле
.
В данном случае т=3т₁
и

Момент
инерции обруча найдем, восполь-­
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-­
извольной
оси;
J₀
—
момент
инерции отно-­
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-­
мулу
к обручу, получим

Рис. 6.3

Подставив
выражения J₁
и
J₂
в форму­лу
(2), найдем момент инерции маятника
относительно оси вра­щения:

Расстояние
l_С
от
оси маятника до его центра масс равно

Подставив
в формулу (1) выражения J,
l_с
и массы маятника

, найдем период его колебаний:

После
вычисления по этой формуле получим
T=2,17
с.

Пример
5. Складываются
два колебания одинакового направле-­
ния,
выражаемых уравнениями
;
х₂=
=,
где А₁=1
см,
A₂=2
см,

с,

с, ω
=
=.
1. Определить начальные фазы φ₁
и φ
₂
составляющих коле-

баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:

(2)

Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:

рад и

рад.

2.
Для определения амплитуды А
результирую­щего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим

(3)

где

— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ₂
и φ₁
получим

рад.

Рис. 6.4

Подставим
значения А₁
,
А₂
и

в формулу (3)
и
произведем вычисления:

A=2,65
см.

Тангенс
начальной фазы φ
результирующего колебания опреде-­
лим
непосредственно из рис. 6.4:

, отку-­
да
начальная фаза

Подставим
значения А₁,
А₂,
φ
₁,
φ
₂
и произведем вычисления:

= рад.

Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде

, где A=2,65
см,
,

рад.

Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравне­ния
которых

(1).

(2)

где
a₁=1
см,
A₂=2
см,
.
Найти уравнение траектории точ-­
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.

Решение.
Чтобы
найти уравнение траектории точки,
ис­ключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-

зуемся
формулой
.
В данном случае

, поэтому

Так
как согласно формуле (1)
,
то уравнение траекто-­
рии

(3)

Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.

Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию

см, и составим таблицу:

X , СМ	-1	—0,75	—0,5	0	+0,5	+ 1
у, см	0	±0,707	±1	±1,41	±1,73	±2

Начертив
координатные оси и выбрав масштаб,
нанесем на пло­скость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колеба­ния
в соответствии с уравнениями движе­ния
(1) и (2) (рис. 6.5).

Рис. 6.5

Для
того чтобы указать направление движения
точки, проследим за тем, как из­меняется
ее положение с течением времени. В
начальный момент t=0
координаты точ­ки
равны x(0)=1
см и y(0)=2
см. В по­следующий
момент времени, например при t₁=l
с,
координаты точек изменятся и ста­нут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последую­щий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в мо­мент
t₂
= 2 с колеблющаяся точка достиг­нет
точки D,
она
будет двигаться в обратном направлении.

Задачи

Кинематика
гармонических колебаний

6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с^-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.

6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
коле­баний,
заданных уравнением
,
где ω=2,5π
с^-1,
τ=0,4
с.

6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.

6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.

Механические колебания и волны

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Отличительными признаками колебательного движения являются:

• повторяемость движения;
• возвратность движения.

Для существования механических колебаний необходимо:

• наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
• наличие малого трения в системе.

Механические волны – это процесс распространения колебаний в упругой среде.

Виды волн

• Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.

• Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.

Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

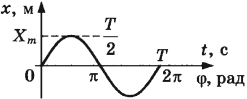
где ​( x )​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​( A )​ – амплитуда колебаний; ​( omega t+varphi_0 )​ – фаза колебаний; ​( omega )​ – циклическая частота; ​( varphi_0 )​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

где ​( v )​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

где ​( a )​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ​( F )​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где ​( W_k )​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

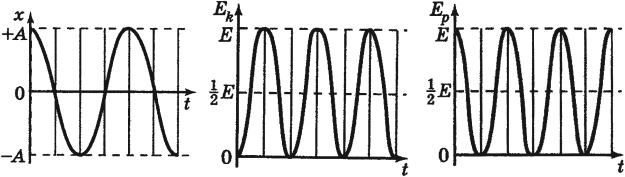
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:

• потенциальная энергия равна нулю;
• кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

• кинетическая энергия равна нулю;
• потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Амплитуда и фаза колебаний

Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ​( A, (X_{max}) )​, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ​( varphi )​, единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
​( varphi_0 )​ – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период колебаний

Период колебаний – это время одного полного колебания.
Обозначение – ​( T )​, единицы измерения – с.

Период гармонических колебаний – постоянная величина.

Частота колебаний

Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ​( nu )​, единицы времени – с^-1 или Гц (Герц).

1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ​( omega )​, единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

• при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
• силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.

При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.

Период колебаний математического маятника:

Частота колебаний математического маятника:

Циклическая частота колебаний математического маятника:

Максимальное значение скорости колебаний математического маятника:

Максимальное значение ускорения колебаний математического маятника:

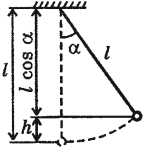
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:

Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:

Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:

Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ​( h )​, определяется по формуле:

где ​( l )​ – длина нити, ​( alpha )​ – угол отклонения от вертикали.

Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.

Период колебаний пружинного маятника:

Частота колебаний пружинного маятника:

Циклическая частота колебаний пружинного маятника:

Максимальное значение скорости колебаний пружинного маятника:

Максимальное значение ускорения колебаний пружинного маятника:

Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:

Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.

Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.

Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.

Резонанс

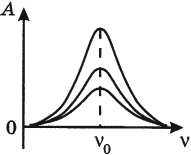
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.

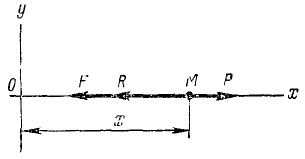
Условие резонанса:

​( v_0 )​ – собственная частота колебаний маятника.

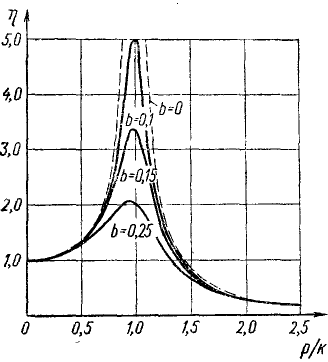
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.

Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.

Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ​( lambda )​, единицы измерения – м.

Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.

Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​( nu )​ < 16 Гц);
• звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
• ультразвук (( nu ) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

• от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

• от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.

Основные формулы по теме «Механические колебания и волны»

Содержание:

Колебания материальной точки:

К исследованию колебаний одной материальной точки могут быть сведены многие технические задачи

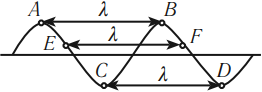
В качестве примера интегрирования дифференциальных уравнений движения рассмотрим колебания материальной точки. Еще совсем недавно изучение колебаний не входило в программу курсов теоретической механики высших учебных заведений. Но необходимость создания новых методов расчета всевозможных машин и различных сооружений, обладающих большой прочностью при небольшом весе, а также необходимость увеличения скоростей и производигельности машин стимулировали быстрое развитие раздела динамики, называемого теорией колебаний. Раздел, посвященный колебаниям, включен теперь во все программы по теоретической механике. 

C основами явлений колебаний удобно ознакомиться сперва на примере, колебания одной материальной точки. Изучение вибраций одной материальной точки интересно также и потому, что к вибрации точки могут быть непосредственно приведены многие практически важные задачи.

Пусть точка M массы m притягивается к точке О силой F, пропорциональной (рис. 162) расстоянию ОМ, а начальная скорость точки M направлена по прямой OM или равна нулю. В таком случае точка M будет двигаться по прямолинейной траектории, вдоль которой мы направим ось х. Начало координат возьмем в точке О (в равновесном положении). Сила F как бы стремится вернуть точку M в равновесное положение О, за что ее называют восстанавливающей силой. Примером такой силы могут служить сила упругости стержня, совершающего малые колебания, или равнодействующая сил веса G и натяжения T нити при малых колебаниях маятника и т. и. Чем больше координата х, тем больше величина этой силы. Вместе с тем сила (точнее говоря, ее проекция на ось Ох) по знаку всегда противоположна знаку координаты х. В самом деле, если точка M находится справа от x начала координат О, то координата х положительна, а сила направлена в отрицательную сторону, и наоборот, если координата х отрицательна, то восстанавливающая сила направлена в положительную сторону. Обозначив коэффициент пропорциональности между силой и расстоянием через с (причем с > 0), выразим восстанавливающую силу формулой

F= — сх.        (131)

Рис. 162

Пусть на точку M во время ее движения действует сила сопротивления R, пропорциональная скорости точки и направленная против скорости. Таким образом, если точка M движется вправо (х > 0), то сила сопротивления направлена влево (R < 0), и, наоборот, если х < 0, то R > 0. Обозначив коэффициент пропорциональности через а (причем а > 0), мы определим силу сопротивления (выражаясь точнее, ее проекцию на ось Ох) формулой

R = — ах.        (132)

Кроме того, пусть на точку M действует возмущающая сила Р, т. е. некоторая дополнительная сила, вызывающая изменение движения, обусловленного основной силой F. Возмущающая сила направлена по прямолинейной траектории точки M и, периодически изменяя свою величину и знак, раскачивает точку M то в ту, то в другую сторону. Мы ограничимся рассмотрением простейшего случая и предположим, что сила P изменяется с течением времени по закону синуса:

P = H sin pt.        (133)

Очевидно, что сила P изменяется в пределах от +Н до —Н. Пример такой силы приведен в задаче № 110.

Напишем дифференциальное уравнение движения точки M:

Разделив обе части уравнения на т, введем обозначения

        (134)

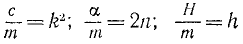
и перенесем члены, содержащие х или его производные, влево:

х + 2nx + k²x =h sin pt.    (135)

Мы имеем неоднородное линейное дифференциальное уравнение с постоянными коэффициентами. Общее решение такого уравнения складывается из: 1) общего решения соответствующего однородного уравнения, т. е. уравнения (135) без правой части, и какого-либо частного решения неоднородного уравнения (135).

Для интегрирования уравнения

х + 2nx + k²x = 0

составим характеристическое уравнение

z² + 2nz + k² = 0.

Если n < k («малое сопротивление»), то характеристическое уравнение имеет комплексные корни:

и общее решение однородного уравнения имеет вид

    (136)

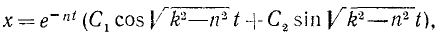
где C₁ и C₂ — постоянные интегрирования. Эти постоянные можно определить лишь после того, как будет получено частное решение неоднородного уравнения (135).

Частное решение неоднородного уравнения (135) при p≠k будем искать вида

х= В sin (pt — δ).

Подберем такие постоянные В и δ, при которых написанное выражение удовлетворяет уравнению (135). Найдем первую и вторую производные от х по времени:

x = Bp cos (pt— δ); х — — Bp² sin (pt— δ)

и подставим в (135) написанное выражение х и его производных:

— Bp² sin (pt — δ) + 2nBp cos (pt — δ) + k²B sin (pt — δ) = h sin pt.

Преобразуем правую часть этого равенства:

h sin pt = h sin (pt — δ +δ) = h sin (pt — δ) cos ∂ + h cos (pt — δ) sin δ.

Перенеся все члены влево и собирая члены, содержащие sin(pt— δ) и cos (pt — δ), получим

[В (k²—p²)-h cos δ] sin (pt — δ) + (2Bnp-hsin δ) cos (pt — δ) = O.

Это равенство обращается в тождество, если

В (k²— р²) = h cos δ; 2Bnp = h sin δ,

или

    (137)

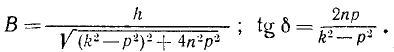
Складывая общее решение (136) однородного уравнения с найденным частным решением неоднородного уравнения, получим общее решение неоднородного уравнения (135) в таком виде:

    (138)

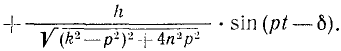
Прежде чем исследовать сложное колебательное движение точки под действием сил F, R и P, выражаемое уравнением (138), рассмотрим более простые движения, которые точка совершала’ бы под действием одной силы F или же под действием силы F и какой-либо- одной из двух остальных R или Р.

Точка, движущаяся по прямой, совершает под действием восстанавливающей силы гармоническое колебание

Свободные колебания без сопротивления

Предположим, что на материальную точку M (см. рис. 162 на стр. 274) действует только восстанавливающая сила (131), сила же сопротивления (132) и возмущающая сила (133) равны нулю. Пусть начальная скорость точки M направлена по прямой MO или равна нулю. В таком случае точка M будет двигаться по прямой OM (по оси Ох), дифференциальное и кинематическое уравнения ее движения мы получим, положив в (135) и в (138) n и h равными нулю. В самом деле, если сила сопротивления R=O, то, следовательно, α = 0, потому что R=— ах и х переменная величина. Если же a = 0, то равно нулю и n, которое согласно (134) равно 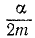. Аналогично, равенство нулю возмущающей силы означает, что равны нулю H и h.

В таком случае уравнение (135) принимает вид

х + k₂x = 0,    (139)

а его интеграл

х = C₁ cos kt + C₂sin kt.     (139^/)

Этому уравнению придадим более удобный вид, для чего выразим, постоянные интегрирования C₁ и C₂ через две другие постоянные величины А и β, однозначно связанные с C₁ и C₂ соотношениями

C_{1 =} A sinβ и C_{2 =} A cos β.    (140″)

Тогда

x = A sin (kt+ β).    (140)

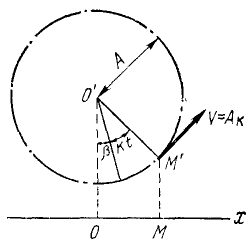
Это уравнение является одним из важнейших уравнений в теории колебаний и описывает наиболее простое колебательное движение, называемое гармоническим. Еще в древности было известно, что если некоторая точка M’ (рис. 163) равномерно движется по окружности радиуса О’М’ — А со скоростью kA, то проекция M этой точки на какую-либо ось Ох, лежащую в плоскости окружности, совершает гармонические колебания. Мы воспользуемся рис. 163, чтобы нагляднее ознакомить читателя с параметрами гармонического колебания. 

Рис. 163

Если точка M’ опишет полную окружность, то точка M’ совершит одно полное колебание.

Время одного полного колебания точки M (или, что то же, время,в течение которого точка M’ описывает одну полную окружность) называют периодом -τ₀ колебаний. 

Угловая скорость k, с которой поворачивается радиус-вектор при равномерном движении точки M’, равна циклической, круговой или угловой частоте колебаний точки М. Эту величину обычно коротко называют частотой, хотя, как будет видно из дальнейшего, оба понятия не вполне идентичны.

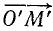
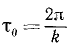
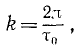
Период и угловая частота связаны простым соотношением, которое становится очевидным, если учесть, что τ₀—это время, в течение которого , вращаясь с угловой скоростью k, поворачивается на 2π:

 и      (141)

или ввиду (134)

     (142)

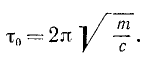
Период имеет размерность времени

[τ] = T¹.

Частота имеет размерность угловой скорости

[k] = T¹.

Из (141) видно, что круговая частота k равна числу полных колебаний, совершаемых в 2π сек. Частота ν колебаний пропорциональна круговой (циклической, угловой) частоте k и равна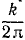. В технике и в физике частоту обычно измеряют в герцах (гц). 1 гц — частота, равная одному полному колебанию (циклу) в секунду. Иначе говоря, герц есть частота такого периодического процесса, который повторяется каждую секунду. Обратите внимание на то, что частота и период гармонических колебаний зависят от массы точки и коэффициента с восстанавливающей силы и не зависят от начальных данных.

Максимальное отклонение А точки M от среднего (равновесного) положения О в ту или в другую сторону (или, что то же, радиус круговой траектории точки М’) называют амплитудой. Амплитуду измеряют в единицах длины:

[A] = T¹.

Аргумент синуса (kt + β) называют фазой колебания, a β—начальной фазой. Физический смысл фазы колебания выявляется при сравнении двух колебаний с одинаковыми частотами, но с разными начальными фазами. Колебание с фазой (kt+ β) опережает колебание с фазой kt, а колебание с фазой (kt — β) отстает от него (разумеется, при положительном β).

Напомним, что А и β являются постоянными интеграции, а следовательно, их определяют по начальным данным. Пусть в начальное мгновение t = 0, x=x₀ и x=x₀. Продифференцировав (140) по времени, получим х = Ak cos (kt + β), и подставляя начальные значения:

х₀ =  A sinβ и х₀ = Ak cos β,

получим 

      (143)

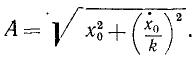
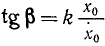
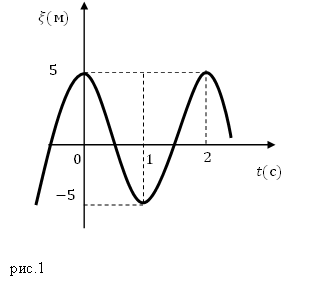
Из тех же равенств можно определить и начальную фазу . Амплитуда и начальная фаза зависят от частоты и от начальных данных.

Задача №1

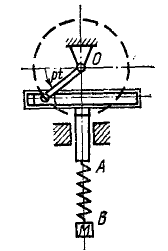
Груз весом 2 T подвешен на тросе (рис. 164). При равномерном спуске груза со скоростью υ = 5м/сек произошла неожиданная задержка верхнего конца троса вследствие защемления троса в обойме блока. Пренебрегая весом троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса с = 4 T/см.

Решение. Примем следующие единицы измерений: длина—в см, время — в сек, сила—в Т. Рассмотрим движение груза. На груз действуют две силы: вертикально вниз вес груза 2T, вертикально вверх — натяжение троса. Груз спускался равномерно, следовательно, до защемления натяжение троса равнялось весу груза. В этом равновесном положении его застала авария. После защемления троса груз не остановился мгновенно. В это мгновение он имел скорость 5 м/сек и продолжал опускаться. Но по мере опускания груза сила натяжения троса возрастала от своего начального значения 2T. Ускорение груза направлено по силе и пропорционально ей. Поэтому опускание груза было замедленным и в некоторое мгновение скорость груза, перейдя через нуль, стала направленной вверх, в направлении силы и ускорения. Движение вверх было ускоренным, но по мере того как груз поднимался, растяжение троса, а следовательно, и его натяжение уменьшались, а потому уменьшалось ускорение груза, скорость же продолжала увеличиваться до момента прохождения через равновесное положение. После этого груз, набрав скорость, продолжал подниматься, ио замедленно, так как натяжение троса стало меньше силы веса и равнодействующая приложенных к грузу сил была направлена вниз. Затем скорость стала равной нулю, груз начал падать вниз, натяжение троса возрастало и движение повторялось снова неопределенное количество раз.

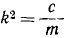
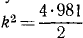
Начало О системы отсчета выберем обязательно в равновесном положении груза, относительно которого происходят колебания, направив ось Ox вертикально вниз (рис. 164). В начальное мгновение (в момент защемления троса) было: x₀= 0; x₀= 500 см/сек. Квадрат круговой частоты определим по (134). После подстановки в формулу имеем . Определим амплитуду по формуле (143):

Таким образом, при равновесном положении груза натяжение троса равно 2T; когда же груз опустился на одну амплитуду, то трос растянулся еще на 11,28 см, а при жесткости троса в 4 T/см натяжение его увеличилось еще на 45,12 Т.

Ответ. 47,1 T.

Натуральный логарифм отношения двух последующих амплитуд затухающих колебаний называют логарифмическим декрементом

Свободные колебания с сопротивлением

Движение под действием восстанавливающей силы и силы сопротивления будем называть свободными колебаниями. Мы только что убедились, что свободные колебания без сопротивления являются гармоническими и, раз возникнув, они повторялись бы до тех пор, пока их не прекратила бы или не изменила бы какая-нибудь внешняя сила. Пусть возмущающая сила отсутствует (P = 0, H = 0, h = 0), а на точку действуют силы F=-cx и R =—ах. Дифференциальное уравнение (135) движения точки M принимает вид

х + 2nx 4- k²x = 0,    (144)

а его интеграл получим, положив в (138) h=0:

или, если воспользуемся соотношениями (140),

    (145)

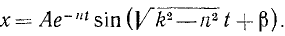
Постоянные А и β определяют по начальным данным.

Наиболее существенное отличие уравнения (145) от уравнения (140), иначе говоря, наиболее существенное изменение в свободном колебании точки М, внесенное наличием силы сопротивления, заключается в множителе e^-nt, который с течением времени непрерывно уменьшается, вследствие чего амплитуда Ae^-nt колебаний с сопротивлением убывает по экспоненциальному закону, асимптотически приближаясь к нулю. Такое колебание называют затухающим.

Переходя к определению периода затухающих колебаний, обратим внимание на то, что вообще периодом периодического движения называют промежуток времени между двумя последовательными прохождениями точки (или системы) через одно и то же положение водном и том же направлении. В случае затухающих колебаний только равновесное положение удовлетворяет такому определению периода, через всякое же другое положение точка M (или любая система, совершающая затухающие колебания) проходит через неравные промежутки времени (см. рис. 165). Поэтому под периодом затухающих колебаний понимают промежуток времени τ₁ между двумя последовательными прохождениями точки M (или системы) через положение равновесия в одинаковом направлении. В таком же смысле колебания, описываемые уравнением (145), могут быть названы изохронными. Период затухающих колебаний можно определить но формуле

    (146)

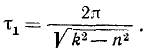
Проф. И. М. Бабаков в учебнике «Теория колебаний» рекомендует для практических расчетов более удобную формулу:

    (146^/)

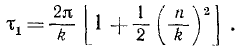
Сравнивая (141) и (146), мы видим, что сопротивление увеличивает период свободных колебаний, но незначительно.

Гораздо больше оно влияет на убывание амплитуд. Так, например, при n = 0,05 k сопротивления увеличивают период на 0,125%, а амплитуда за время одного полного колебания уменьшается более чем на 25%. На рис. 165 изображен график затухающих колебаний для случая n = 0,05 k, позаимствованный из «Лекций» проф. Е. Л. Николаи.

Отношение абсолютных значений двух последовательных амплитудных отклонений точки от равновесного положения называют коэффициентом затухания:

    (147)

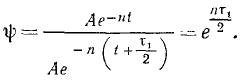
Для характеристики быстроты убывания амплитуды удобнее пользоваться натуральным логарифмом коэффициента затухания, называемым логарифмическим декрементом колебаний:

    (147^/)

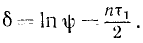
На рис. 165 пунктиром изображены кривые, уравнения которых x= Ае^-n и х = —Ae^-nt. График затухающих колебаний расположен между этими двумя кривыми и поочередно их касается.

Задача №2

Маятник, масса которого равна 1 кг и период качания в безвоздушной среде τ₀=l сек, заставили качаться вереде, сопротивляющейся но закону R =—2х н. Определить: 1) период затухающих колебаний маятника и 2) уменьшение амплитуды в течение трех периодов.

Решение. Определим параметры колебаний.

Круговая частота. Период τ₀=l сек=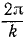 , откуда k=2π = G,28.

Коэффициент α=2; m=1; 2n=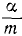, откуда n=l.

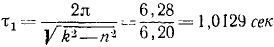
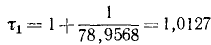
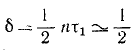
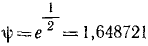
Период затухающих колебаний , или по (146′),
. Логарифмический декремент . Коэффициент затухания .

Отношение каждого максимального отклонения к последующему (через полпериода) равно коэффициенту затухания, следовательно, если амплитуду при первом размахе принять за 1, то следующие уменьшаются в отношении .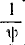

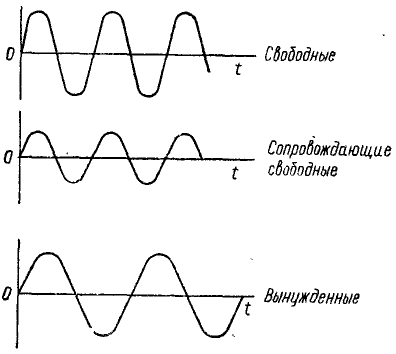
Под действием восстанавливающей и возмущающей сил точка совершает сложное колебание, являющееся результатом наложения трех гармонических колебаний: свободного, сопровождающего свободного и вынужденного

Вынужденные колебания без сопротивления

Пусть на точку М, движущуюся по оси Ох, действуют две силы — восстанавливающая F=— CX и возмущающая P =H sin pt, направленные также по оси Ох. Величина pt может быть названа фазой силы, постоянную р назовем круговой частотой возмущающей силы, а период этих изменений обозначим через τ. Действие сопротивления мы пока не учитываем, поэтому, положив в уравнении (135) n = 0, получим следующее дифференциальное уравнение вынужденных колебаний без сопротивления:

x+ k²x = h sin pt.    (148)

Чтобы найти решение этого уравнения, надо в (138) положить равным нулю не только n, но и δ, так как согласно (137) δ = 0 при n = 0. Имеем

Определим постоянные. Если в начальное мгновение х = x₀ и x = χ₀, то

и

    (149)

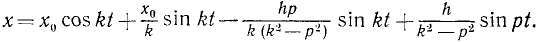
Первые два слагаемых описывают свободные колебания с частотой k. Воспользовавшись соотношениями (140″), эти два слагаемых можно представить в виде x₁ = A sin (kt + β). Если в начальное мгновение х = х= 0, то эти колебания во все время действия возмущающей силы не возникают. Третье слагаемое

— гармоническое колебание, происходящее с частотой k свободных колебаний, но с амплитудой, зависящей от возмущающей силы. Это колебание всегда, при любых начальных условиях, сопровождает вынужденные колебания и его называют свободным сопровождающим колебанием. Четвертое слагаемое

    (149^/)

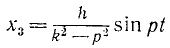
описывает вынужденные колебания. Таким образом, колебания точки являются результатом линейного наложения трех гармонических колебаний: 1) свободных, 2) сопровождающих свободных и 3) вынужденных (рис. 166):

    (149^//)

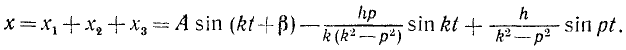
Рис. 166

На схеме (рис. 166) приведены только частоты этих колебаний, но разумеется, не изображены амплитуды и начальные фазы.

Вынужденные колебания происходят с частотой р, равной частоте возмущающей силы. Они не зависят от начальных данных.

Как видно из (143), для изменения амплитуды свободных колебаний достаточно изменить начальное отклонение или начальную скорость. Напротив, для изменения амплитуды вынужденных колебаний надо изменить возмущающую силу, что обычно бывает сопряжено с необходимостью преобразования конструкции.

Если частота р вынужденных колебаний меньше частоты k собственных (случай «малой» частоты), то амплитуда вынужденных колебаний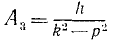, а фаза pt вынужденных колебаний совпадет
с фазой pt возмущающей силы. По если р > k (случай «большой» частоты), то выражение, написанное для А₃, становится отрицательным, однако амплитуда не может быть отрицательной. Это кажущееся несоответствие объясняется тем, что при р > k фаза вынужденных колебаний противоположна фазе возмущающей силы и уравнение вынужденных колебаний имеет вид

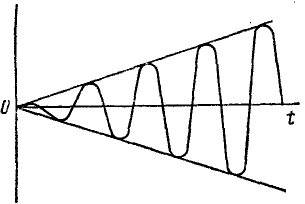
Резонанс

Если частоты собственных и вынужденных колебаний близки между собой, то амплитуды получаются очень большими. Напомним, что при интегрировании уравнения (135) мы положили p≠k. Если р= k, то дифференциальное уравнение (148) имеет вид

x-k²x = h sin kt    (148′)

Будем искать частное решение вида

x= Bt cos kt.

Определив х =— 2Bk sin kt— Btk² cos kt и подставив его вместе с х в дифференциальное уравнение, получим
— 2Bk sin kt = h sin kt,

откуда 

Находим общее решение дифференциального уравнения движения:

Дифференцируем по времени:

Если в начальное мгновение x=x₀ и x=x₀, то

и общее решение принимает вид

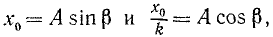
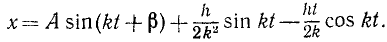
или, полагая  получим

    (148»’)

Следовательно, и при равенстве частот движение точки состоит из трех колебательных движений, однако вынужденные колебания представлены непериодическим членом, в коэффициент которого входит множителем время. C течением времени это третье слагаемое, называемое вековым членом, безгранично растет по абсолютной величине. Размах вынужденных колебаний непрерывно растет по линейному закону. Это явление называется резонансом. График вынужденных колебаний при резонансе представлен на рис. 167.

Рис. 167

Задача №3

Груз M подвешен в точке В к пружине AB (рис. 168), верхний конец А которой прикреплен к поступательно движущейся кулисе. Кривошип кулисного механизма имеет длину а = 0,02 м и вращается с угловой скоростью , вследствие чего точка А совершает гармонические колебания по закону х_А =0,02 sin 7t м. Определить вынужденные колебания груза М, если его вес G = 3,6 н, а жесткость пружины с = 36 н/м.

Рис. 168

Решение. Составим дифференциальное уравнение движения груза М. Начало координат выберем в точке, с которой центр тяжести груза совладал в момент начала движения (при t = 0), когда верхний конец А пружины, совершающей гармонические колебания вместе с кулисой, занимал свое среднее положение. При сделанном нами выборе начала отсчета (в равновесном положении груза) вес G = 3,6 н уравновешивался статическим натяжением пружины с λ_cr = 36 ∙ 0,1. Наличие этих двух взаимно уравновешенных сил эквивалентно их отсутствию, а потому мы можем их отбросить и в дальнейшем рассматривать движение центра тяжести груза лишь под действием натяжения пружины, обусловленного только ее динамической деформацией, т. е. только деформацией пружины при колебании груза около равновесного положения.

При t ≠ 0 положение центра тяжести груза определяется координатой х, получающейся от суммирования двух перемещений: динамической деформации пружины и перемещения a sin pt верхнего конца А пружины. Следовательно, динамическая деформация пружины равна разности перемещений ее нижнего конца В и верхнего конца А, т. е. равна х—α sin pt . Дифференциальное уравнение движения центра груза имеет вид

mx = — с (х—a sin pt).

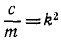
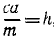
Деля обе части уравнения на m и вводя обозначения и , придадим этому уравнению знакомый нам вид (148)

x + k²x = h sin pt,

где 

Подставляя в (149′), находим вынужденные колебания груза.
Ответ. 0,04 sin 7t.

Задача №4

Статический прогиб рессор товарного вагона равен 5 см. Определить критическую скорость вагона, при которой начнется «галопирование» вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания на рессорах: длина рельсов равна 12 м.

Решение. Жесткость рессор 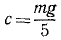, частота собственных колебаний

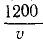
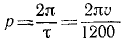
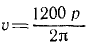
Если поезд идет со скоростью υ см/сек, то вагон получает толчки на стыках через каждые сек. Таков период τ возмущающей силы. Частота возмущающей силы , откуда . Галопирование вагона произойдет при резонансе, т. е. при равенстве частот собственных и вынужденных колебаний. Подставляя в выражение, полученное для скорости, р = k = 14, найдем

Чтобы выразить скорость в км/ч, умножим выраженную в см/ceκ скорость на 0,036.

Ответ. υ=96 км/ч.

Если к точке приложены восстанавливающая и возмущающая сила и сила сопротивления, то свободные колебания затухают и остаются только вынужденные

Влияние сопротивления на вынужденные колебания

Если на точку, кроме восстанавливающей и возмущающей сил, действует также и сила R сопротивления, то движение точки описывается дифференциальным уравнением (135) и его решением (138).

Первый член правой части (138) с возрастанием t стремится к нулю, и соответствующие ему колебания точки с течением времени затухают, поэтому ими можно пренебречь. Остаются только вынужденные колебания (рис. 169):

     (150)

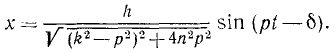
Они происходят с частотой возмущающей силы, сопротивление не влияет на период вынужденных колебаний. Амплитуда не зависит от начальных условий и времени и не изменяется с течением времени.

Предположим, что возмущающая сила сохраняет свое максимальное значение Н. При равновесии под действием такой силы и восстанавливающей силы F =— сх точка M получила бы так называемое статическое отклонение

Из этого соотношения найдем максимальное ускорение точки M под действием возмущающей силы: h=k²x_ст и, подставляя это значение h в выражение (150), выразим амплитуду вынужденных колебаний равенством

Отношение частоты вынужденных колебаний к частоте собственных колебаний

                 (151)

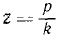
носит название коэффициента расстройки и отношение величины n, измеряемой в ceκ^-1, к частоте собственных колебаний называют безразмерным коэффициентом вязкости:

              (151′)

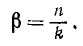
Введя эти обозначения в предыдущее равенство и разделив обе части его на x_ст, получим:

                 (152)
 

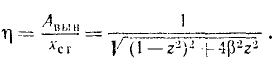
Рис. 169

Величина η—коэффициент динамичности — позволяет охарактеризовать динамический эффект, вызываемый возмущающей силой.

Коэффициент динамичности η зависит от двух величин (z и β).

Задавшись каким-либо значением β, и откладывая по оси абсцисс различные значения z, а по оси ординат—соответствующие значения коэффициента динамичности η, получим, так называемые, резонансные кривые. На рис. 170 изображены резонансные кривые для значений безразмерного коэффициента вязкости: 0,25, 0,15. и 0,10. Пунктиром нанесена уходящая в бесконечность при 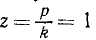резонансная кривая, соответствующая β = 0, т. е. вынужденным колебаниям без сопротивления.

Как показывает график (рис. 170) в областях, достаточно далеких от резонанса, амплитуды вынужденных колебаний с сопротивлением почти не зависят от безразмерного коэффициента вязкости. В этих областях при вычислении амплитуд вынужденных колебаний можно не учитывать сопротивлений и пользоваться более простой формулой

Рис. 170

При резонансе (р = k) амплитуда вынужденных колебаний при наличии сопротивлений остается конечной, но наибольшее значение амплитуда имеет, если 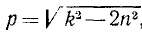, в чем легко убедиться, определив максимум амплитуды при различных р, считая h, k и п данными.

В вынужденных колебаниях с сопротивлением всегда бывает сдвиг фазы колебания по отношению к фазе .возмущающей силы. Величина этого сдвига определяется формулой (137).

Заметим, что все сказанное здесь относительно малых колебаний материальной точки полностью соответствует малым колебаниям материальной системы с одной степенью свободы.

Формула частоты в физике

Формула частоты

Чаще всего в физике частоту обозначают буквой $nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

[nu =frac{1}{T}left(1right).]

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

[nu =frac{N}{Delta t}left(2right),]

где $Delta t$ — время за которое происходят $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

[left[nu right]=с^{-1}=Гц.]

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${nu }_1 и {nu }_2$) равна:

[{nu =nu }_1- {nu }_2left(3right).]

Еще одно величиной характеризующей колебательный процесс является циклическая частота (${omega }_0$), связанная с частотой как:

[{omega }_0=2pi nu left(4right).]

Циклическая частота измеряется в радианах, деленных на секунду:

[left[{omega }_0right]=frac{рад}{с}.]

Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

[nu =frac{1}{2pi sqrt{{m}/{k}}}left(5right).]

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

[nu =frac{1}{2pi sqrt{{l}/{g}}}left(6right),]

где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

[nu =frac{1}{2pi sqrt{{J}/{mgd}}}left(7right),]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:

[n=frac{1}{tau }left(8right).]

Единицей измерения частоты дискретных событий является обратная секунда:

[left[nright]=frac{1}{с}.]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:

[n=frac{1}{tau }left(9right).]

Примеры задач с решением

Читать дальше: формулы математического маятника.