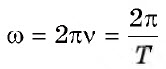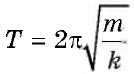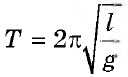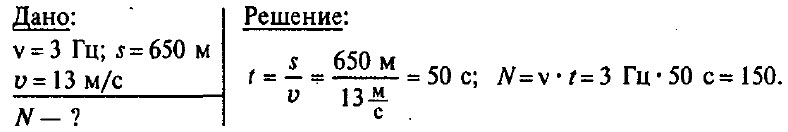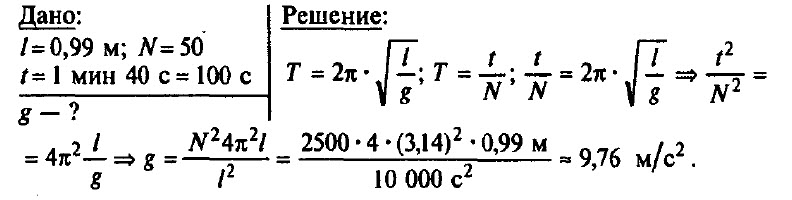Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.
Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.
По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.
Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?
Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.
Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.
Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?
Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?
Краткая теория для решения Задачи на Механические колебания.
Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Частота колебаний, теория и онлайн калькуляторы
Частота колебаний
Гармонические колебания, частота и др их характеристики
Определение
Колебаниями называют такие движения или процессы, которые повторяются.
По своей природе колебания делят на механические, электромагнитные и др. Разные виды колебаний описывают при помощи одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания являются свободными (собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешние воздействия на эту систему отсутствуют.
Самым простым видом колебаний являются гармонические колебания. Гармоническими колебаниями называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:
[s=A{cos ({omega }_0t+varphi ) } left(1right),]
где $A=s_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ — фаза колебаний. Величина $s$ лежит в пределах $-Ale sle $+A.
Промежуток времени через который повторяются определенные состояния системы (T) называют периодом. За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:
[T=frac{2pi }{{omega }_0}left(2right).]
Разные процессы, повторяющиеся через равные промежутки времени (периодические процессы) можно представить в виде совокупности наложенных гармонических колебаний.
Определение частоты колебаний
Определение
Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $). Частота колебаний — это количество полных колебаний, которые совершаются за единицу времени.
[nu =frac{1}{T}left(3right).]
Из (2) и (3) следует, что циклическая частота равна:
[{omega }_0=2pi nu left(4right).]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
[left[nu right]=с^{-1}=Гц.]
Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса называется в честь немецкого ученого Г. Герца.
Циклическая частота измеряется в радианах, деленных на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Частота дискретных событий, частота вращения
Определение
Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.
Если время, которое занимает одно событие обозначить как $tau $, то частота дискретных событий равна:
[n=frac{1}{tau }left(5right).]
Единицей измерения частоты дискретных событий является обратная секунда:
[left[nright]=frac{1}{с}.]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $tau $ — время, затрачиваемое на один полный оборот, то:
[n=frac{1}{tau }left(6right).]
Примеры задач с решением
Пример 1
Задание. Каковы: циклическая частота колебаний и частота колебаний величины $r$, если ее гармонические колебания заданы уравнением:
[r=0,5{cos left(3pi t+frac{pi }{4}right)(м) . }]
Решение.Рассмотрим уравнение колебаний параметра $r$:
[r=0,5{cos left(3pi t+frac{pi }{4}right)left(мright)(1.1) . }]
Из этого уравнения мы видим, что амплитуда колебаний равна $r_{max}=0,5 (м)$; ${omega }_0=3pi $ ($frac{рад}{с}$). Частоту колебаний ($nu $) найдем, используя формулу:
[{omega }_0=2pi nu left(1.2right).]
Выразим $nu $, имеем:
[nu =frac{{omega }_0}{2pi } left(1.3right).]
Подставляя ${omega }_0=3pi $textit{ }($frac{{rm рад}}{{rm с}}$) получаем:
[nu =frac{3pi }{2pi }=frac{3}{2}left(Гцright).]
Ответ. ${omega }_0=3pi $ $frac{рад}{с};;$ $nu $=1,5 Гц
Пример 2
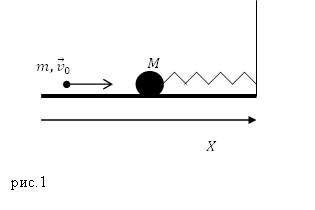
Задание. Шар массой $M$ закреплен на пружине коэффициент упругости, которой равен $k$. Шар лежит на гладкой горизонтальной поверхности (рис.1). Горизонтально летела пуля, ее скорость составляла $v_0 $, была направлена в сторону шара и в момент удара была параллельна оси пружины, масса пули $m$. После удара о шар пуля застряла в нем. Какова частота колебаний шара, вызванных ударом пули. Шар может скользить по столу без трения. Массу пружины и сопротивление воздуха не учитывать.
Решение. После того, как пуля ударила по шарику и застряла в нем, данная система будет совершать колебания. Так как по условию задачи колебания можно считать свободными (трения нет), то колебания шарика (с пулей) на пружине являются свободными и гармоническими, их можно описать как, например изменение координаты шарика, который примем за материальную точку:
[x=x_m{sin left({omega }_0t+varphi right)left(2.1right). }]
В таких колебаниях кинетическая энергия переходит в потенциальную энергию и наоборот, поэтому можно записать закон сохранения энергии в виде:
[frac{(m+M)v^2_m}{2}=frac{kx^2_m}{2} left(2.2right),]
где $frac{(m+M)v^2_m}{2}$ — кинетическая энергия системы в момент, сразу следующий за ударом, скорость шарика с пулей максимальна; $frac{kx^2_m}{2}$ — потенциальная энергия сжатой пружины в момент максимального ее сжатия, когда шарик с пулей перестаёт двигаться.
Амплитуду скорости колебаний найдем как:
[v_x=frac{dx}{dt}=frac{d}{dt}(x_m{sin left({omega }_0t+varphi right)=x_m{omega }_0{cos left({omega }_0t+varphi right)to v_m= }x_m{omega }_0(2.3). }]
Подставим $v_m$ в (2.2), имеем:
[frac{(m+M){x_m}^2{{omega }_0}^2}{2}=frac{kx^2_m}{2}to {omega }_0=sqrt{frac{k}{m+M}}left(2.4right).]
Применим выражение:
[nu =frac{{omega }_0}{2pi } left(2.5right).]
Найдем частоту колебаний системы:
[nu =frac{1}{2pi }sqrt{frac{k}{m+M}}.]
Ответ. $nu =frac{1}{2pi }sqrt{frac{k}{m+M}}$
Читать дальше: частота.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
2019-12-12
Найти частоту «симметричных» колебаний системы, показанной на рисунке. Массы всех шаров $m$, коэффициенты упругости пружинок $k$.
Решение:
Прежде всего найдем силу, действующую на каждый шарик при его смещении из положения равновесия (рис.). Обозначим начальное расстояние шарика от центра системы (точки О) $x_{0}$, новое расстояние — $x$, смещение шарика от положения равновесия — $Delta x$, начальную длину пружины — $l_{0}$ ее длину в растянутом состоянии — $l$, а изменение длины пружины — $Delta l$.
Как видно из рисунка б,
$l_{0} = 2x_{0} cos 30^{ circ}$ и $l = 2x cos 30^{ circ}$.
Тогда каждая из пружин при смещении шариков окажется растянутой иа величину
$Delta l = l — l_{0} = 2 (x — x_{0} ) cos 30^{ circ} = sqrt{3} Delta x$.
Следовательно, на каждый шарик со стороны пружин будут действовать две равные по абсолютной величине силы: $F = k Delta l = sqrt{З} k Delta x$.
Равнодействующая этих сил направлена к положению равновесия шарика и равна по абсолютной величине (см. рис.) $F^{ prime} = 2F cos 30^{ circ} = 3k Delta x$, то есть пропорциональна смещению шарика от положения равновесия. Это означает. что система эквивалентна системе из трех обычных пружинных маятников, соединенных в точке О и имеющих жесткость $k^{ prime} = 3k$ каждый. Поэтому частота колебаний системы будет равна
$omega = sqrt{ frac{k^{ prime} }{m} } = sqrt{ frac{3k}{m} }$.
Евгений трохов
[56.6K]
более года назад
Частота колебаний — это число колебаний в единицу времени.
Единица измерения -1 Гц( одно колебание а секунду)
Находим:
50/2 минуты=25 колеб. /мин=
=25/60 Гц=(5/12) Гц.
Пеоиод колебаний-, это время одного колебания.
Находится, как величина, обратная к частоте :
Т=1/(5/12)=12/5=2,4 секунды
Ответ :частота m( букву греческого алфавита «мю» не могу набрать) =5/12 Гц
Период Т=2,4 сек
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Явление резонанса заключается в том, что амплитуда установившихся вынужденных колебаний достигает наибольшего значения, когда частота вынуждающей силы равна собственной частоте колебательной системы.
Отличительной особенностью вынужденных колебаний является зависимость их амплитуды от частоты изменения внешней силы. Для изучения этой зависимости можно воспользоваться установкой, изображенной на рис. 1.61. На кривошипе с ручкой укреплен пружинный маятник. При равномерном вращении ручки на груз через пружину передается действие периодически изменяющейся силы. Изменяясь с частотой, равной частоте вращения ручки, эта сила заставит груз совершать вынужденные колебания. Если вращать ручку кривошипа очень медленно, то груз вместе с пружиной будет перемещаться вверх и вниз так же, как и точка подвеса О. Амплитуда вынужденных колебаний при этом будет невелика. При более быстром вращении груз начнет колебаться сильнее, и при частоте вращения, равной собственной частоте пружинного маятника (ω = ωсоб), амплитуда его колебаний достигнет максимума. При дальнейшем увеличении частоты вращения ручки амплитуда вынужденных колебаний груза опять станет меньше. Очень быстрое вращение ручки оставит груз почти неподвижным: из-за своей инертности пружинный маятник, не успевая следовать изменениям внешней силы, будет просто дрожать на месте.
Явление резонанса можно продемонстрировать и с нитяными маятниками. Подвесим на рейке массивный шар 1 и несколько маятников, имеющих нити разной длины (рис. 1.62). Каждый из этих маятников имеет свою собственную частоту колебаний, которую можно определить, зная длину нити и ускорение свободного падения.
Теперь, не трогая легких маятников, выведем шар 1 из положения равновесия и отпустим. Качания массивного шара вызовут периодические колебания рейки, вследствие которых на каждый из легких маятников начнет действовать периодически изменяющаяся сила упругости. Частота ее изменений будет равна частоте колебаний шара. Под действием этой силы маятники начнут совершать вынужденные колебания. При этом маятники 2 и 3 останутся почти неподвижными. Маятники 4 и 5 будут колебаться с немного большей амплитудой. А у маятника 6, имеющего такую же длину нити и, следовательно, собственную частоту колебаний, как у шара 1, амплитуда окажется максимальной. Это и есть резонанс.
Резонанс возникает из-за того, что внешняя сила, действуя в такт со свободными колебаниями тела, все время совершает положительную работу. За счет этой работы энергия колеблющегося тела увеличивается, и амплитуда колебаний возрастает.
Резкое возрастание амплитуды вынужденных колебаний при ω = ωсоб называется резонансом.
Изменение амплитуды колебаний в зависимости от частоты при одной и той же амплитуде внешней силы, но при различных коэффициентах трения ц, изображено на рис. 1.63, где кривой 1 соответствует минимальное значение р, кривой 3 — максимальное.
Из рис. 1.63 видно, что о резонансе имеет смысл говорить, если затухание свободных колебаний в системе мало. Иначе амплитуда вынужденных колебаний при ω = ω0 мало отличается от амплитуды колебаний при других частотах.
Явление резонанса в жизни и в технике
Явление резонанса может играть как положительную, так и отрицательную роль.
Известно, например, что тяжелый «язык» большого колокола может раскачать даже ребенок, но при условии, что будет тянуть за веревку в такт со свободными колебаниями «языка».
На применении резонанса основано действие язычкового частотомера. Этот прибор представляет собой набор укрепленных на общем основании упругих пластин различной длины. Собственная частота каждой пластины известна. При контакте частотомера с колебательной системой, частоту которой нужно определить, с наибольшей амплитудой начинает колебаться та пластина, частота которой совпадает с измеряемой частотой. Заметив, какая пластина вошла в резонанс, мы определим частоту колебаний системы.
С явлением резонанса можно встретиться и тогда, когда это совершенно нежелательно. Так, например, в 1750 г. близ города Анжера во Франции через цепной мост длиной 102 м шел в ногу отряд солдат. Частота их шагов совпала с частотой свободных колебаний моста. Из-за этого размахи колебаний моста резко увеличились (наступил резонанс), и цепи оборвались. Мост обрушился в реку.
В 1830 г. по той же причине обрушился подвесной мост около Манчестера в Англии, когда по нему маршировал военный отряд.
В 1906 г. из-за резонанса разрушился Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон.
Теперь для предотвращения подобных случаев войсковым частям при переходе через мост приказывают «сбить ногу», идти не строевым, а вольным шагом.
Если же через мост проезжает поезд, то, чтобы избежать резонанса, он проходит его либо на медленном ходу, либо, наоборот, на максимальной скорости (чтобы частота ударов колес о стыки рельсов не оказалась равной собственной частоте моста).
Собственной частотой обладает и сам вагон (колеблющийся на своих рессорах). Когда частота ударов его колес на стыках рельсов оказывается ей равной, вагон начинает сильно раскачиваться.
Явление резонанса встречается не только на суше, но и в море, и даже в воздухе. Так, например, при некоторых частотах гребного вала в резонанс входили целые корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания частей самолета, что он разваливался в воздухе.