Аннотация: Для получения более полной характеристики вариационного ряда помимо средней величины рассчитываются так называемые структурные показатели. К ним относятся мода, медиана, квартили, децили, перцентили, квартильные и децильные коэффициенты.
8.1. Мода
Мода (Мо) — это наиболее часто встречающееся значение признака, или иначе говоря, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному.
8.1.1. Определение моды в дискретных вариационных рядах
В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды.
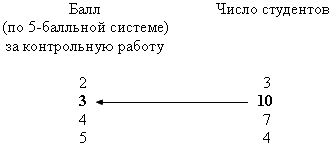
Пример 8.1. По представленным ниже результатам проведения контрольной работы по статистике определим моду.
Здесь наибольшая частота — 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами за контрольную работу, была «тройка».
8.1.2. Определение моды в интервальных вариационных рядах с равными интервалами
Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
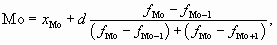
где хМо — нижняя граница модального интервала;
d — величина интервала;
fMo — частота модального интервала;
fMo — 1 — частота интервала, предшествующего модальному;
fMo + 1 — частота интервала, следующего за модальным.
Пример 8.2. Имеются данные по группе банков.
| Сумма выданных кредитов, млн ден. ед. | Количество банков |
|---|---|
| До 40 | 8 |
| 40-60 | 15 |
| 60-80 | 21 |
| 80-100 | 12 |
| 100-120 | 9 |
| 120-140 | 7 |
| 140 и выше | 4 |
| Итого | 77 |
Определим модальный размер выданных кредитов:
- модальным является интервал 60-80, так как ему соответствует наибольшая частота (21);
- нижняя граница модального интервала xМо = 60; величина интервала d = 20 (80 — 60 = 20);
- частота модального интервала fМо = 21; частота интервала, предшествующего модальному, fМо — 1 = 15; частота интервала, следующего за модальным, fМо + 1 = 12.
Подставив в формулу соответствующие величины, получим
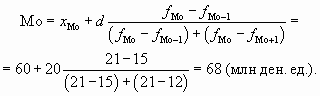
Определить модальное значение признака можно и по графику. Для этого в случае дискретных вариационных рядов строится полигон распределения. Напомним, что у него на оси абсцисс помещаются значения признака (варианты), а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующее наибольшей вершине полигона, будет значением моды.
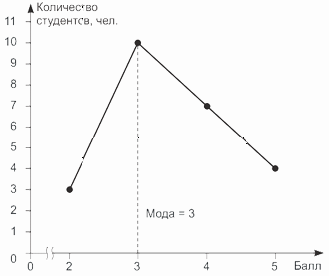
Пример 8.3. По результатам проведения контрольной работы по статистике, приведенным в примере 8.1, определим моду графическим способом.
Для этого построим полигон распределения и найдем абсциссу его вершины (рис. 8.1).
Рис.
8.1.
Определение моды по полигону распределения
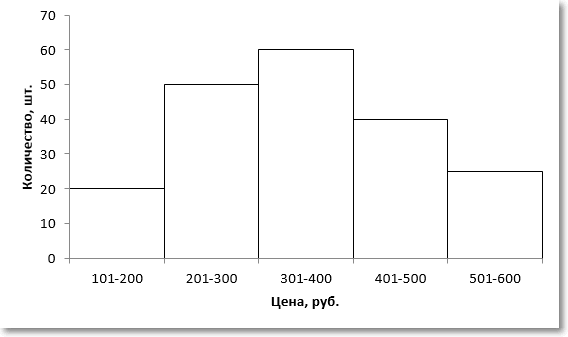
Если имеется интервальный вариационный ряд с равными интервалами, то для определения моды строится гистограмма, у которой на оси абсцисс находятся значения границ интервалов, а на оси ординат — соответствующие интервалам частоты. На гистограмме модальный интервал будет иметь наибольшую высоту столбца. Затем надо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса точки пересечения будет значением моды. Продемонстрируем это на примере.
Пример 8.4. По данным о распределении банков по сумме выданных кредитов, приведенным в примере 8.2, определим моду графическим способом (рис. 8.2).
Рис.
8.2.
Определение моды по гистограмме распределения
Вариационный ряд может содержать несколько модальных значений. Чаще всего это происходит, когда в один ряд объединяют разнородные единицы наблюдения, которые желательно разделить на подгруппы и анализировать по отдельности. Вариационный ряд, имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.
В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств.
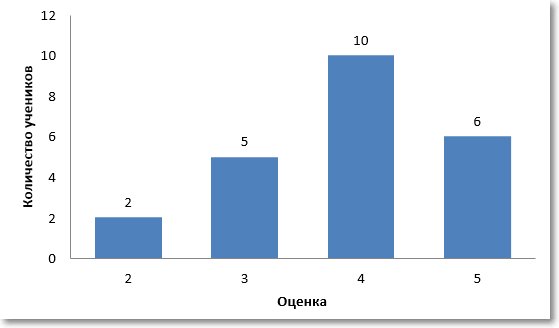
Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Но набор числовых данных может иметь разное распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 человек 2 школьника написали контрольную работу на двойку, 5 – на тройку, 10 – на четверку и 6 – на пятерку. Это и есть распределение оценок. Распределение очень наглядно можно представить с помощью специальной диаграммы – гистограммы. Для данного примера получится следующая гистограмма.
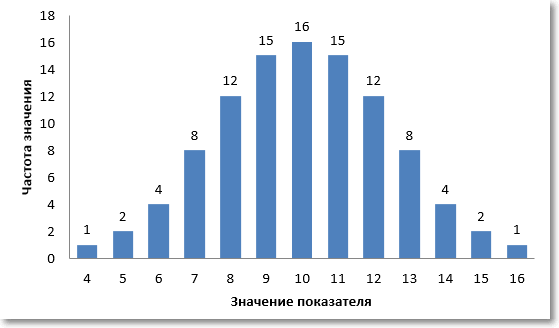
Во многих случаях количество уникальных значений намного больше, а распределение похоже на нормальное. Ниже приведена примерная иллюстрация нормального распределения случайных чисел.
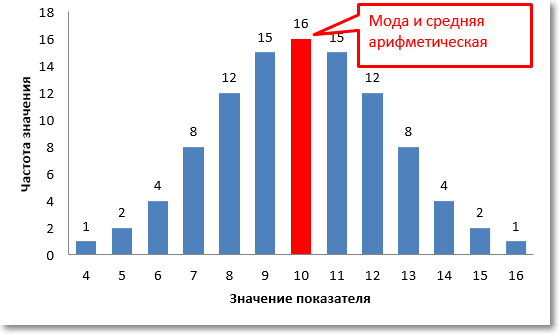
Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.
Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.
На диаграмме оба значения центральной тенденции совпадают и равны 10.
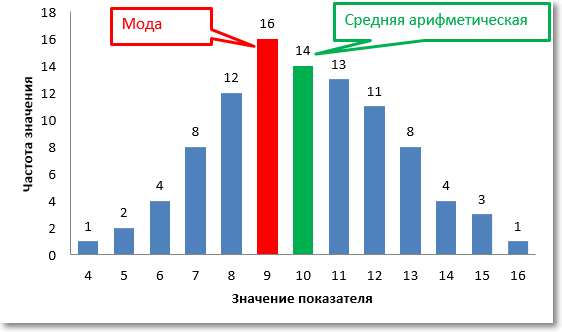
Но такое распределение встречается далеко не всегда, а при малом числе данных – совсем редко. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.
На рисунке выше среднее арифметическое по-прежнему составляет 10, а вот мода уже равна 9. Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода.
Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель.
Расчет моды
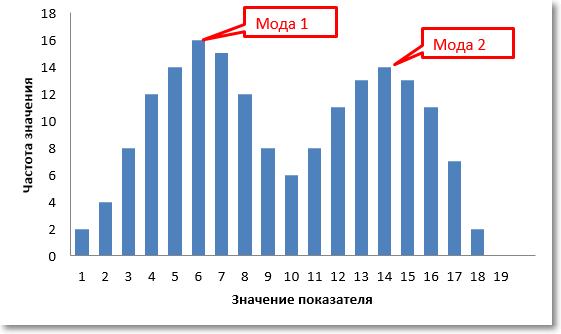
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
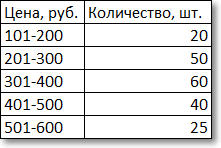
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
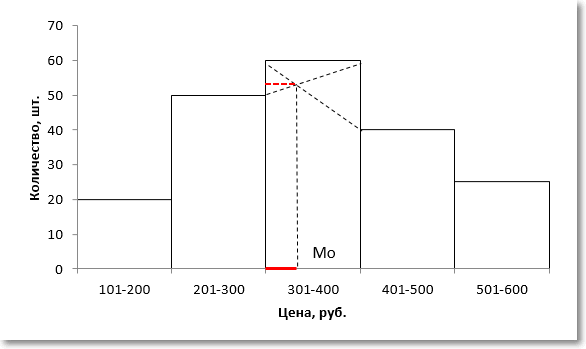
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x0 – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Расчет моды в Excel
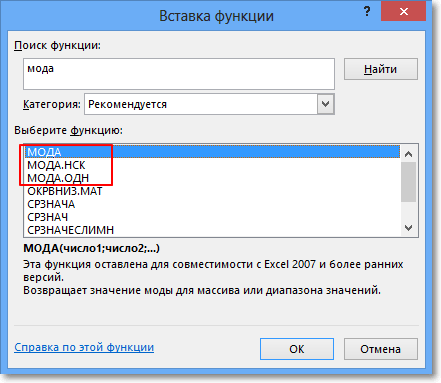
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Следующая статья посвящена медиане.
До встречи на statanaliz.info.
Поделиться в социальных сетях:
В равноинтервальных
рядах
распределения мода определяется по
формуле:
где ХМо
– нижняя граница модального интервала
(модальным называется интервал, имеющий
наибольшую частоту)
h
– величина модального интервала;
fMo,
fMo-1,
fMo+1–
частота модального, предмодального и
следующего за модальным интервалов.
Пример 9.
Таблица 28 —
Распределение выручки по группам
магазинов
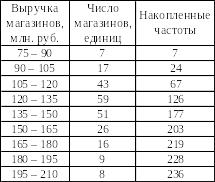
Модальный интервал
120-135 млн. руб., так как наиболее часто
(59 раз) встречается в анализируемой
совокупности.
В данном случае
мода будет равна:
Таким образом, в
рассматриваемой совокупности магазинов
наиболее часто встречаемое значение
выручки – 130 млн. рублей.
Полученный результат
можно подтвердить при помощи графического
изображения. Для определения моды
проведем диагональ через вершины самого
высокого столбца (модального интервала)
как показано на гистограмме (рисунок
11).
Мода определяется
проекцией точки пересечения этих линий
на ось абсцисс.
Если предмодальный,
модальный и послемодальный интервалы
имеют одинаковую
величину,
моду можно определить как внутренним
пересечением, так и внешним пересечением
(на рисунке обозначено пунктиром), если
же перечисленные интервалы имеют
различную величину, то мода определяется
только внутренним пересечением.
Рисунок 11 –
Графическое определение моды по
гистограмме
В равноинтервальном
вариационном ряду медиана определяется
следующим образом:
где ХМе
– нижняя граница медианного интервала
(медианным называется интервал, которому
соответствует накопленная частота,
равная или превышающая полусумму частот
интервального вариационного ряда);
h
– величина медианного интервала;
fMе–
частота медианного интервала;
SМе-1
– накопленная частота домедианного
интервала.
Пример 10.
По данным таблицы
28 медиана будет равна:
В связи с тем, что
номер медианы равен 118,5, следовательно
медианным интервалом будет:120-135 (так
как этому интервалу соответствует
накопленная частота равная, либо
превышающая номер медианы)
Таким образом, в
рассматриваемой совокупности магазинов
118 из них имеют выручку до 133 млн. рублей,
а другие 118 – более этой величины.
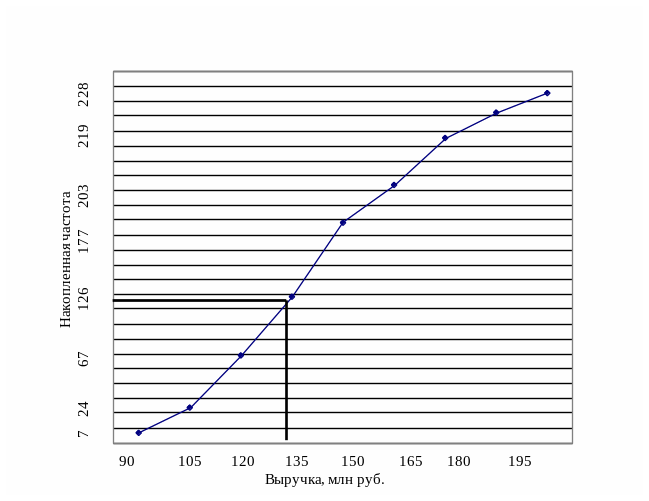
Рисунок 12 –
Графическое определение медианы по
кумуляте
3.4 Расчет модальной величины в неравноинтервальных рядах распределения1
Одной из наиболее
интересных в методологическом плане
работ при определении структурных
характеристик ряда распределения
является нахождение моды по группировке
с неравными интервалами. Неравные
интервалы применяются в статистике,
когда значение признака варьирует
неравномерно и в значительных размерах,
что характерно для большинства
социально-экономических явлений,
особенно при анализе макроэкономических
показателей.
В условиях неравных
интервалов становится очевидной
невозможность применения уже известных
формул. Поэтому возникает необходимость
в поиске новых методик.
В качестве решения
вставшей проблемы используем два метода
расчета структурной характеристики в
неравных интервалах: графический и
вычислительный методы. Для большей
наглядности и простоты приведенных
методов рассмотрим нахождение моды на
конкретном примере.
Пример 11.
Имеются следующие
данные:
Таблица 29 –
Распределение 40 стран мира по калорийности
питания населения
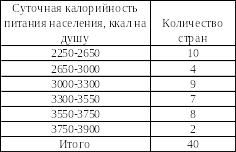
На основании
представленных данных мы приходим к
выводу, что имеется группировка с
неравными интервалами. Опишем процесс
решения по шагам.
Шаг 1.
Построим расчетную таблицу 30, в которой
наряду с имеющимися в таблице 29 данными
приведем расчетную графу «Плотность
распределения».
Причем плотность
распределения – отношение количества
наблюдений в группе – частот либо
частостей — к величине интервала группы.
Таблица 30 –
Расчетная таблица для определения моды
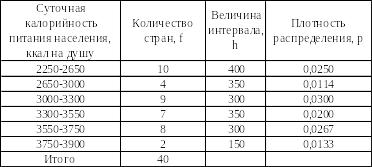
Шаг
2. Определим моду при помощи
графического изображения. Для этого
используем гистограмму. На графике по
оси абсцисс откладываем интервалы, а
по оси ординат – соответствующие им
плотности распределения, так как в
группировке с неравными интервалами
модальный интервал определяется по
наибольшей плотности распределения.

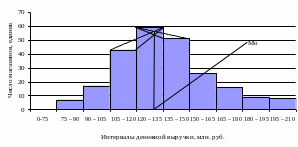
Рисунок 13. Плотность
распределения40тран мира по суточной
калорийности питания, ккал на душу
населения
После того, как
график построен, определим наивысший
столбец. Он, в нашем случае, и будет
модальным. Проекция точки пересечения
линий опускаем перпендикуляр на ось
абсцисс – модальное значения, и, таким
образом, получаем приближенное значение
моды. Так, по рисунку 13 можно определить,
что мода приблизительно равна 3600 ккал.
Шаг 3.
Определение моды расчетным путем.
Расчет модального
значения для вариационных рядов с
неравными интервалами можно осуществлять
и по формуле, аналогичной приведенной
выше (пример 9, раздел 3.3), но вместо
показателей частот (частостей) используются
показатели абсолютной и относительной
плотности распределения, которые
обеспечивают сопоставимость неравных
интервалов.
Абсолютная плотность
распределения определяется по формуле:
Формула для расчета
относительной плотности распределения
имеет вид:
,
где f-
частота интервала,
F –
частость интервала,
h –
величина интервала.
Учитывая приведенные
выше обозначения и данные таблицы 30
модальное значение рассмотренного
примера определяется по формуле:
,
где
— величина плотности распределения
модального, домодального и послемодального
интервалов.
В нашем случае
мода равна:
Следовательно,
наиболее часто встречающимся значением
калорийности питания в указанных странах
явялется 3612,0 ккал на душу населения.
Таким образом
комплексное использование графического
и расчетного методов является эффективным
методом проверки правильности полученного
результата.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
8.4. МОДА и МЕДИАНА (структурные средние)
Мода и медиана наиболее часто используемые в экономической практике структурные средние.
Мода – это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.
Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:
(8.16 – формула Моды)
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.
В дискретном ряду медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы.
В случае интервального вариационного ряда медиану определяют по формуле:

где хо – нижняя граница медианного интервала;
NМе– порядковый номер медианы (Σf/2);
S Me-1 – накопленная частота до медианного интервала;
fМе – частота медианного интервала.
Пример вычисления Моды.
Рассчитаем моду и медиану по данным табл. 8.4.
Таблица 8.4 – Распределение семей города N по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)
| Группы семей по размеру дохода, руб. | Число
семей |
Накоп-
ленные частоты |
в % к итогу |
| До 5000 | 600 | 600 | 6 |
| 5000-6000 | 700 | 1300
(600+700) |
13 |
| 6000-7000 | 1700 (fМо-1) | 3000 (S Me-1 )
(1300+1700) |
30 |
| 7000-8000
(хо) |
2500
(fМо) (fМе) |
5500 (S Me) | 55 |
| 8000-9000 | 2200 (fМо+1) | 7700 | 77 |
| 9000-10000 | 1500 | 9200 | 92 |
| Свыше 10000 | 800 | 10000 | 100 |
| Итого | 10000 | – | – |
Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:
Пример вычисления Моды
Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):
1) сначала находим порядковый номер медианы: NМе = Σfi/2= 5000.
2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее значение медианы определим по формуле (8.17):
Пример вычисления Медианы
Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.
Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения
Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.
Если Мо<Ме<Х – имеет место правосторонняя асимметрия.
При Х<Ме<Мо следует сделать вывод о левосторонней асимметрии ряда.
Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке
Оценка статьи:
Загрузка…
Структурные средние — мода, медиана, квантиль, дециль
Краткая теория
Наиболее широкое применение в статистике имеют структурные
средние, к числу которых относятся мода и медиана (непараметрические средние).
Мода — величина признака (варианта), которая
встречается в ряду распределения с наибольшей частотой (весом). К моде (Мо)
прибегают для выявления величины признака, имеющей наибольшее распространение
(цена на рынке, по которой было совершено наибольшее число продаж данного
товара, номер обуви, который пользуется наибольшим спросом у покупателей и т.
д.). Мода используется только в совокупностях большой численности. В дискретном
ряду мода находится как варианта, имеющая наибольшую частоту. В интервальном
ряду сначала находится модальный интервал, то есть интервал, обладающий наибольшей частотой, а
затем – приближенное значение модальной величины признака по формуле:
– нижняя граница модального интервала
— величина модального интервала
– частота интервала, предшествующего
модальному
– частота модального интервала
– частота интервала, следующего за модальным
Квантили —
величины, разделяющие совокупность на определенной количество равных по
численности элементов частей. Самый известный квантиль – медиана, делящая совокупность на две равные части. Кроме медианы часто используются квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100
частей.
Медиана —
величина признака у единицы, находящейся в середине ранжированного
(упорядоченного) ряда. Если ряд распределения представлен конкретными
значениями признака, то медиана (Me) находится как
серединное значение признака.
Если ряд распределения дискретный, то медиана находится как
серединное значение признака (например, если число значений нечетное – 45, то
соответствует 23 значению признака в ряду
значений, расположенных в порядке возрастания, если число значений четное – 44,
то медиана соответствует полусумме 22 и 23 значений
признака).
Если ряд распределения интервальный, то первоначально
находят медианный интервал, который содержит единицу, находящуюся в середине
ранжированного ряда. Для определения этого интервала сумму частот
делят пополам и на основании последовательного накопления (суммирования)
частот интервалов, начиная с первого, находят интервал, где расположена
медиана. Значение медианы в интервальном ряду вычисляют по формуле:
— нижняя граница медианного интервала
— величина медианного интервала
— сумма
частот ряда
– сумма накопленных частот в интервалах,
предшествующих медианному
– частота медианного интервала
Квартили — это значения
признака в ранжированном ряду, выбранные таким образом, что 25% единиц
совокупности будут меньше величины
, 25% единиц будут заключены между
и
; 25% —
между
и
,
остальные 25% превосходят
. Квартили определяются по формулам,
аналогичным формуле для расчета медианы. Для интервального ряда:
Децилем
называется структурная переменная, делящая распределение на 10 равных частей по
числу единиц в совокупности. Децилей 9, а децильных
групп 10. Децили определяются по формулам, аналогичным формуле для расчета
медианы и квартилей.
В целом общая формула для расчета квантилей в интервальном
ряду такова:
– порядковый номер квантиля
– размерность квантиля (на сколько частей эти
квартили делят совокупность)
– нижняя граница квантильного
интервала
– ширина квантильного
интервала
— накопленная частота предквантильного
интервала
Для дискретного ряда номер квантиля можно
найти по формуле:
Примеры решения задач
Задача 1
(дискретный ранжированный ряд)
В
результате исследований установлен среднемесячный доход жильцов одного
подъезда:
|
1.5 |
1.8 |
2 |
2.5 |
2.8 |
2.8 |
2.8 |
3.0 |
3.6 |
3.8 |
|
3.9 |
4 |
5.8 |
5.9 |
6 |
6 |
6 |
6.8 |
7 |
7 |
Определите:
Модальный
и медианный доход, квартили и децили дохода.
Решение
Имеем уже ранжированный ряд — значения дохода жильцов распределены по возрастанию.
Мода
— наиболее часто встречающееся значение. В данном случае имеем ряд с двумя
модами.
и
Медиана
— такое значение признака, которое делит упорядоченное множество данных
пополам.
Квартили
— значения признака в ранжированном ряду, выбранные таким образом, что 25%
единиц совокупности будут меньше величины
; 25% единиц будут
заключены между
и
; 25% — между
и
; остальные 25%
превосходят
.
Дицили делят ряд на 10 равных частей:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
(интервальный ряд)
Для
определения среднего размера вклада в кредитном учреждении были получены
следующие данные:
| Размер вклада, тыс.р. | до 10.0 | 10.0-16.0 | 16.0-22.0 | 22.0-28.0 | 28.0-34.0 | Свыше 34.0 |
|
Удельный вес вкладов, % |
5.0 | 8.0 | 15.0 | 22.0 | 30.0 | 20.0 |
Рассчитайте
структурные средние (моду, медиану,
квартили).
Решение
Вычислим моду размера вклада:
Мода — варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
—
начало модального интервала
—
величина интервала
—
частота модального интервала
—
частота интервала, предшествующего модальному
—
частота интервала, следующего за модальным
Таким образом, наибольшее
количество вкладов имеют размер 30,7 тыс.р.
Медиана — варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало
(нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до
медианного
Таким образом, половина вкладов имеет размер до 28 тыс.р.,
другая половина — более 28 тыс.р.
Вычислим квартили:
Таким
образом 25% вкладов меньше 20,8 тыс.р., 25% вкладов
лежат в интервале от 20,8 тыс.р. до 28 тыс.р., 25% лежат в интервале от 28 тыс.р.
до 33 тыс.р., 25% больше величины в 33 тыс.р.
Задача 3
Постройте
графики для вариационного ряда. На графике покажите моду, медиану, среднюю, квартили.
| Возраст детей (лет) | Число детей (доли) |
| 0-3 | 0.15 |
| 3-6 | 0.2 |
| 6-9 | 0.4 |
| 9-12 | 0.2 |
| 12-15 | 0.05 |
Решение
Вычислим
среднюю
: Для этого просуммируем
произведения середин интервалов и соответствующих частот, и полученную сумму
разделим на сумму частот.
Вычисление моды интервального ряда на графике
Построим
гистограмму.
Мода определяется по
гистограмме распределения. Для этого выбирается самый высокий прямоугольник,
который в данном случае является модальным. Затем правую вершину модального
прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А
левую вершину модального прямоугольника – с левым верхним углом последующего
прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось
абсцисс.
Абсцисса точки пересечения
этих прямых и будет модой распределения
Гистограмма
По
гистограмме получаем, что
Вычисление медианы и квартилей интервального ряда на графике
Построим
кумулятивную кривую частот (график накопленных частот)
Кумулятивная кривая частот
На получившимся графике
накопленных частот из последней получившейся точки (в нашем примере) проведем
линию перпендикулярную к оси
она так же
является максимальной высотой. Поделим ее на 4 части. Через полученные точки
строим параллельную оси
линии которая должна пересекать высоту к оси
и кумуляту. От
места пересечения кумуляты опускаем перпендикуляры. Получившиеся точки есть квартили
и медиана (квартиль при
).
Вывод к задаче
Таким образом
средний возраст детей 6,9 лет. Наибольшее количество детей имеют возраст 7,5
лет. Четверть детей младше 4,5 лет, а самая старшая четверть детей старше 9,1
лет. Половина детей имеет возраст менее 7,3 лет, другая половина – более 7,3
лет.