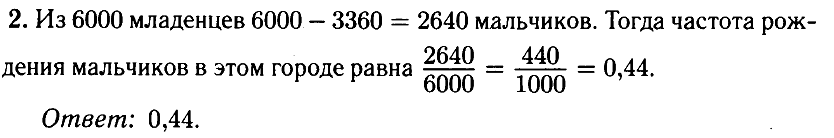Как найти частоту рождаемости в математике

Решение №1751 В некотором городе из 3000 появившихся на свет младенцев 1560 мальчиков.

В некотором городе из 3000 появившихся на свет младенцев 1560 мальчиков. Найдите частоту рождения девочек в этом городе.

Решение:

Всего появилось 3000 младенцев. Из них девочек:

3000 – 1560 = 1440

Частота рождения девочек в этом городе:

Ответ: 0,48.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com ��

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе.

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

ЕГЭ для VIP

ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

ЕГЭ Профиль. Задание № 2.

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 2 проверяет умение использовать элементы теории вероятностей при решении прикладных задач. Для его выполнения понадобится производить действия с дробями и совершать простые вычисления. Задание представляет собой текстовую задачу, которая решается с помощью базовых арифметических операций. В ответе необходимо указать целое или дробное число, записанное в виде конечной десятичной дроби.

План выполнения:

1. Внимательно прочитайте задачу.
2. Выявите число всех элементарных событий и число благоприятствующих событий, не пропустив ни одного из всех возможных исходов и не включая ни одного лишнего.
3. При решении задачи на классическое определение вероятности установите, зависимы (совместны) или независимы (несовместны) элементарные события.
4. Выполните на черновике необходимые вычисления.
5. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на классическое
определение вероятности

Задача № 2 (1). В коробке лежит 40 шаров: 20 чёрных, 4 жёлтых и 16 зелёных. Наугад из коробки достают один шар. Найдите вероятность того, что этот шар будет жёлтым.

Решение:

Ответ: 0,1.

Задача № 2 (2). Участников шахматного турнира разбивают на пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 спортсменов из России, в том числе Пётр Орлов. Найдите вероятность того, что Пётр Орлов будет играть с шахматистом из России.

Решение:

Ответ: 0,4.

Задача № 2 (3). У Дениса в копилке лежит 6 рублёвых, 3 двухрублёвых, 2 пятирублёвых и 4 десятирублёвых монеты. Денис наугад достал из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 60 рублей.

Решение:

Ответ: 0,4.

Задачи на использование теорем
о вероятностях событий

Задача № 2 (4). Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение:

Ответ: 0,96.

Задача № 2 (5). При проверке на вирусное заболевание делают анализ крови. Если анализ выявляет вирус, то результат является положительным. У больных анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на заболевание, действительно больны. Найдите вероятность того, что результат анализа у пациента будет положительным. Ответ округлите до сотых.

Решение:

Ответ: 0,05.

Задача № 2 (6). На экзамене по истории ученик отвечает на один вопрос из списка. Вероятность того, что это вопрос по теме «Крепостное право», равна 0,2. Вероятность того, что это вопрос по теме «Февральская революция», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене ученику достанется вопрос по одной из этих двух тем.

Решение:

Ответ: 0,35.

Тренировочные задания с самопроверкой

№ 2.1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.

№ 2.2. В некотором городе на 6000 появившихся на свет младенцев приходится 3360 девочек. Найдите частоту рождения мальчиков в этом городе.

№ 2.3. Вероятность того, что на тесте по математике ученица Настя верно решит не менее 12 задач, равна 0,84. Вероятность того, что Настя решит больше 11 задач, равна 0,96. Найдите вероятность того, что Настя решит ровно 12 задач.

№ 2.4. Склад освещается двумя фонарями с лампами. Вероятность перегорания лампы одного фонаря в течение одного месяца равна 0,4. Найдите вероятность того, что в течение месяца хотя бы одна лампа не перегорит.

№ 2.5. Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Вы смотрели: ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.