Как вычислить частоту?
ν=NΔt(2), где Δt — время за которое происходят N колебаний. Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды: [ν]=с−1=Гц.
Как определить длину волны по частоте?
Поскольку для всех электромагнитных волн скорость в вакууме (с) одинакова, по частоте легко определить длину волны λ: λ = с/ν. Мы просто делим путь, пройденный светом за секунду, на число колебаний за то же время и получаем длину одного колебания.
Как найти скорость Зная частоту?
Т=1/v , можно получить формулу, выражающую связь длины волны с ее скоростью и частотой: Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней .
Какой частоте соответствует длина волны?
Диапазоны и частоты — общепринятые обозначения
| Диапазон частот | Сокращённое название диапазона | Длина волны |
|---|---|---|
| 30-3000 МГц | УКВ (Ультра короткие волны) | 0,1-10 м |
| 3-30 ГГц | СВЧ (Сверхвысокие частоты) | 1-10 см |
| 30-300 ГГц | КВЧ (Крайне высокие частоты) | 1-10 мм |
| 300-3000 ГГц | ГВЫ (Гипервысокие частоты) | 0,1-1 мм |
•22 февр. 2017 г.
Чему равна частота?
Частота — это количество изменений направления тока за секунду. Для измерения частоты используется международная единица герц (Гц). 1 герц равен 1 колебанию в секунду. Герц (Гц) = 1 герц равен 1 колебанию в секунду.
Как определить частоту и период?
Период колебаний является величиной, обратной частоте колебаний: f = 1/T. Частота колебаний — количественная характеристика периодических колебаний, равная отношению числа циклов колебаний ко времени их совершения.
Как найти частоту сигнала?
Для тестирования частоты, используется встроеное техническое меню «Netmonitor» (Сетевой монитор), которое в каждой модели смартфона вызывается персональным кодом. Список телефонов и кодов Android таких как *#0011# или *#*#4636#*#* или *#*#197328640#*#* можно найти здесь.
Как длина волны связана с частотой?
Длина волны прямо пропорциональна скорости волны и обратно пропорциональна частоте колебаний (прямо пропорциональна периоду колебаний). Поперечные и продольные волны описываются одними и теми же законами.
Какая длина волны для частоты 5 Мгц?
Длина волны ⟷ частота
| № | Диапазон | |
|---|---|---|
| частот | длин волн | |
| 4 | 3-30кГц | 100-10км |
| 5 | 30-300кГц | 10-1км |
| 6 | 300-3000кГц | 1000-100м |
•19 авг. 2013 г.
Как найти длину волны через период?
Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
- Так как период колебаний в волне обратно пропорционален частоте,
- , …
- Калькулятор ниже позволяет по двум известным параметрам формулы посчитать неизвестный.
Как найти Как найти скорость?
Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Как найти скорость длиной волны?
Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны. Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Как найти скорость через частоту и длину волны?
Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах. Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц). Пример: частота этой волны равна 9,94 х 10^8 Гц.
Чему равно волновое число?
Волновое число равно числу радиан волны на отрезке в 1 метр.
Чем больше длина волны тем?
Общее правило: Чем выше частота, тем короче длина волны. И наоборот. Формула для расчета длины волны: Длина волны WiFi сигнала (в метрах)= Скорость света (в м/сек) / Частота сигнала (в герцах).
Как определить частоту по периоду?
Частота (в технике обозначают f) — величина, обратная периоду колебаний Т: f = 1/T.
Чему равен 1 герц?
Для измерения частоты используется международная единица герц (Гц). 1 герц равен 1 колебанию в секунду. Герц (Гц) = 1 герц равен 1 колебанию в секунду. Колебание = Одна полная волна переменного тока или напряжения.
Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и, наоборот –
перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического
(в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом:
F(Гц) = 1/T(с) и соответственно:
T(с) = 1/F(Гц)
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое может оказаться довольно громоздким,
а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим
пройденный материал парой простых онлайн калькуляторов.
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ
Частота колебаний F |
||
Период Т |
А теперь всё то же самое, но наоборот:
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ПЕРИОДУ КОЛЕБАНИЙ
Период колебаний Т |
||
Частота F |
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина –
циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω.
В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно:
ω (рад/с) = 2πF(Гц).
Random converter
- Калькуляторы
- Акустика — звук
Калькулятор звуковой частоты и длины волны
Этот калькулятор определяет длину волны звуковых колебаний (только звуковых!), если известны их частота и скорость распространения звука в среде. Он также может рассчитать частоту, если известны длина волны и скорость или скорость звука, если известны частота и длина волны.
Пример: Рассчитать длину звуковой волны, распространяющейся в морской воде от гидроакустического преобразователя с частотой 50 кГц, если известно, что скорость звука в соленой воде равна 1530 м/с.
Частота
f
Длина волны
λ
Скорость звука
v
или Среда
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета выберите среду или введите скорость звука, затем введите частоту и нажмите кнопку Рассчитать для расчета длины волны. Можно также ввести длину волны и рассчитать частоту.
Определения и формулы
Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха образуются зоны сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются по воздуху в форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха движутся параллельно движению волны. Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него. Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более сильных сжатиях и разрежениях.
Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 — Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 — Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук
Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде постоянная, то длина волны обратно пропорциональна частоте.
При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах. Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35 раз быстрее, чем в воздухе.
Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее их движение будет одинаковым для всех трех типов волн:
или
где
f — частота волны,
v — скорость распространения волны и
λ — длина волны
Продольные и поперечные волны
В различных средах звук распространяется в виде различных видов волн. В жидкостях и газах звук распространяется в виде продольных волн. В твердых телах звук может распространяться как в виде продольных, так и в виде поперечных волн.
Для лучшего понимания обоих типов волн удобно воспользоваться механическим аналогом, которым послужит пружина Слинки. Эта пружина представляет собой модель среды (жидкости или газа). Если ее растянуть, а затем сжимать, а затем отпускать один конец, сжатие в форме волны перемещается вперед, передавая таким образом энергию с одного конца пружины в другой. Если звук распространяется в жидкости или газе, он идет от источника в форме периодических сжатий и разрежений газа или жидкости, которые перемещаются от источника звука.
Мы можем сравнить витки пружины с молекулами воздуха или воды, которые сталкиваются друг с другом. Поскольку направление движения этих сжатий и разрежений параллельно направлению движения самой волны, такие волны называются продольными.
Если начать двигать один конец пружины перпендикулярно ее оси, то создается поперечная волна. Она называется поперечной, потому что движение витков пружины перпендикулярно направлению движения волны по пружине. В такой волне энергия передается вдоль пружины, а ее витки движутся в направлении, перпендикулярном передаче энергии.
Отметим, что в нашем эксперименте пружина представляет собой среду, в которой распространяется волна, и эта среда не движется вместе с волной. Она только колеблется. Это поведение волны легко наблюдать в твердом теле, однако это справедливо также для воздуха, воды и вообще любой жидкости или газа. То есть, колебания переносятся молекулами жидкости или газа, в то время как среднее положение молекул среды не изменяется с течением времени. Это справедливо для любых типов волн.
Примеры
Возьмем на клавиатуре несколько нот и покажем их частоту и длину волны. Предположим, что звук движется в воздухе со скоростью 340 м/с. Тогда можно рассчитать длину волны нот:
| Научное и традиционное название ноты | Частота, Гц | Период, мс | Длина волны, см |
|---|---|---|---|
| A3, ля малой октавы | 220 | 4,55 | 156 |
| A4, ля первой октавы | 440 | 2,27 | 78 |
| A5, ля второй октавы | 880 | 1,14 | 39 |
| A6, ля третьей октавы | 1760 | 0,57 | 19,5 |
Акустика — звук
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса — гармонические и негармонические. Гармонический сигнал — это сигнал, который можно описать следующей функцией:
Здесь A — амплитуда сигнала, w — циклическая частота, а phi — начальная фаза. Может возникнуть логичный вопрос — разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sinalpha = cos(frac{pi}{2}medspace-medspace alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
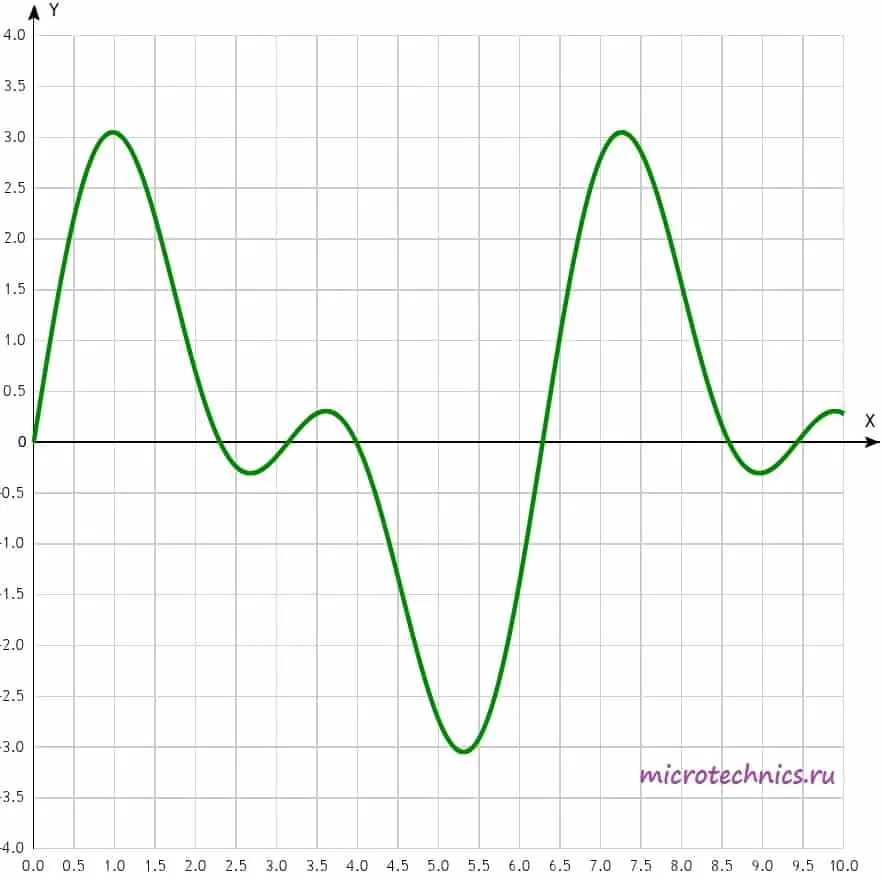
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
Давайте изобразим все эти сигналы на одном графике:
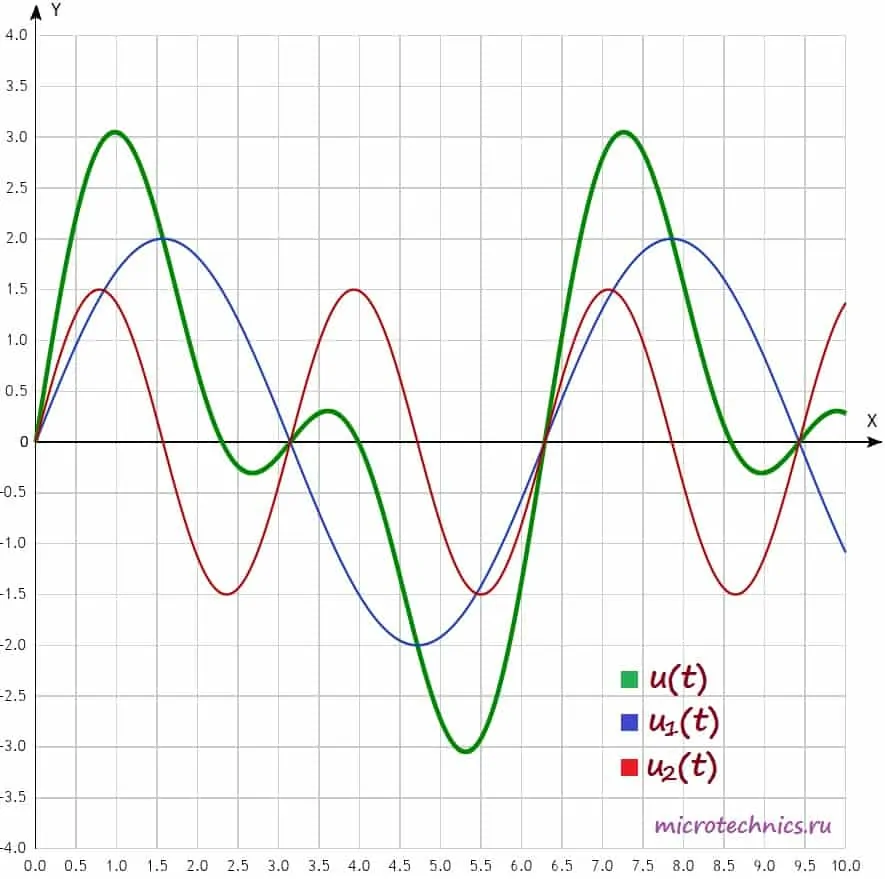
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
u(t) = U_0 + sum_{i=0}^{infty}{U_{k}thinspace sin(thinspace kwt + phi_kthinspace )}
Здесь U_k — амплитуда, а phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
- фазовый спектр сигнала — совокупность начальных фаз всех гармоник
- амплитудный спектр сигнала — амплитуды всех гармоник, из которых складывается негармонический сигнал
Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
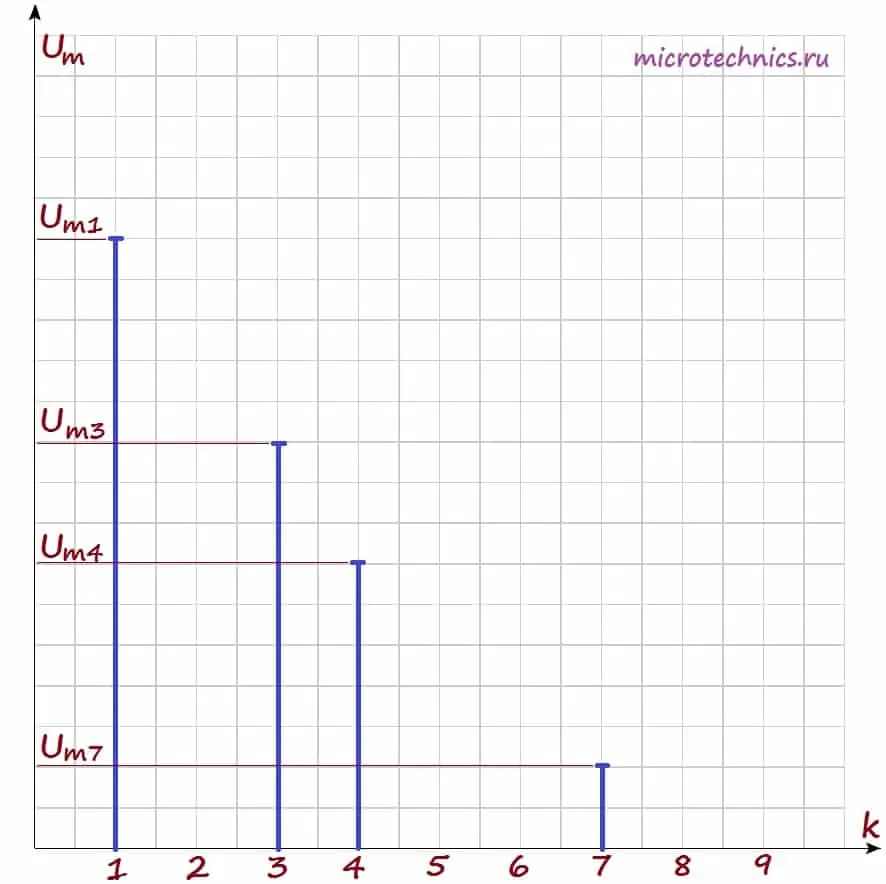
При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
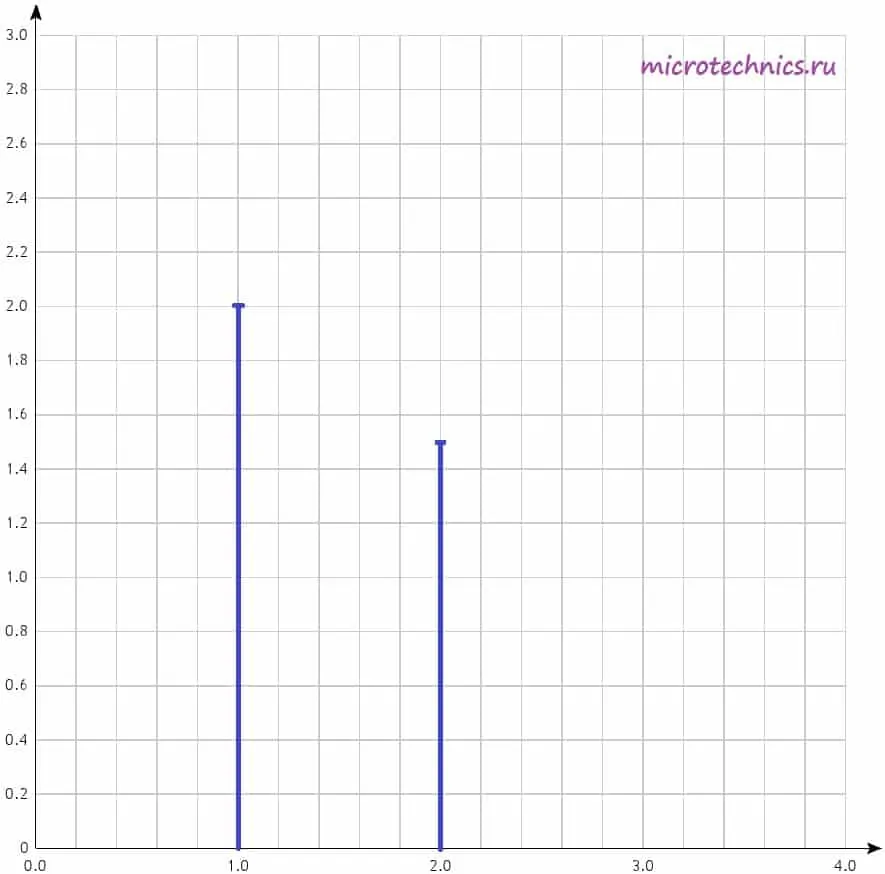
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет…
АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
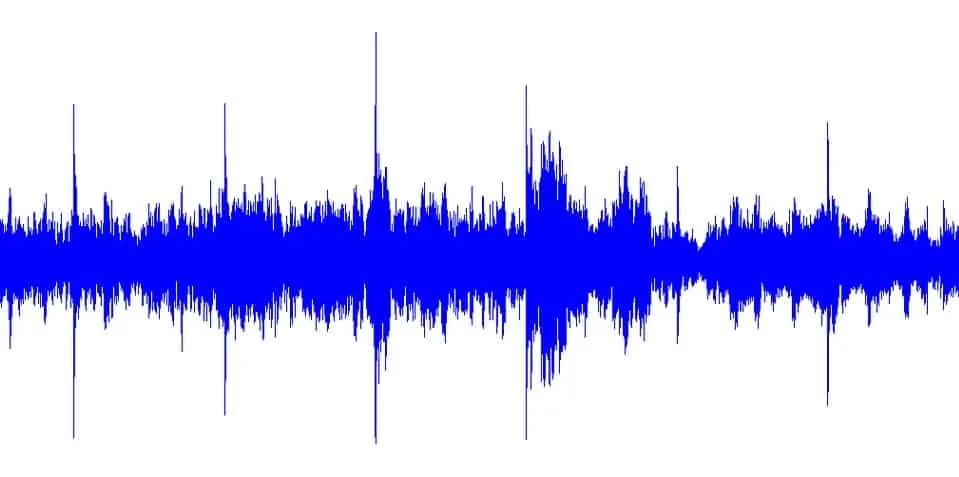
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.
Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
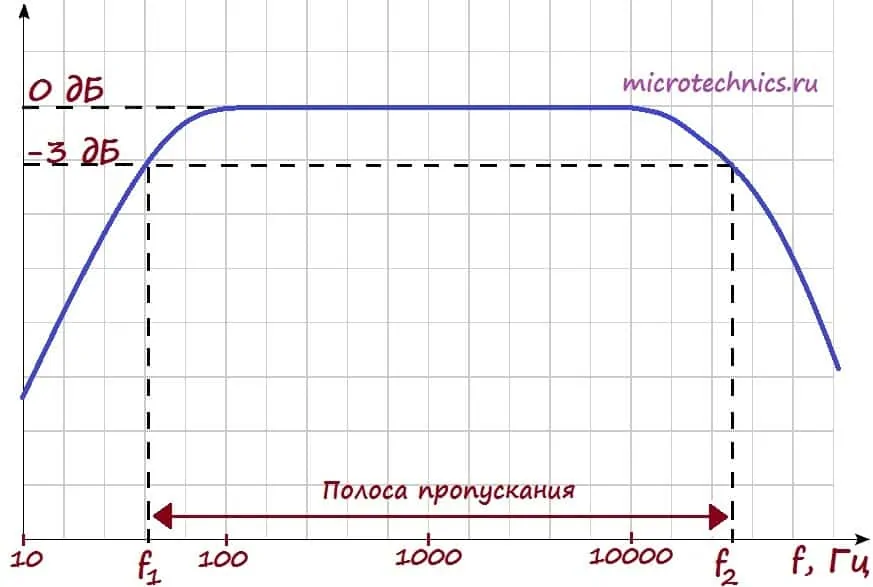
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация — сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
- 20 Гц — 160 Гц — область низких частот
- 160 Гц — 1.28 КГц — область средних частот
- 1.28 КГц — 20.5 КГц — область высоких частот
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:
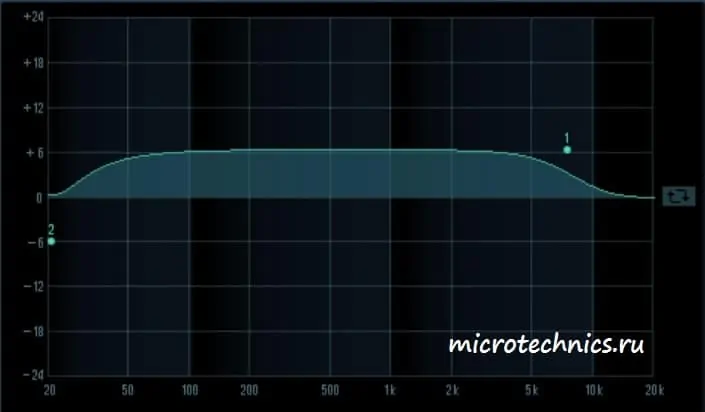
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
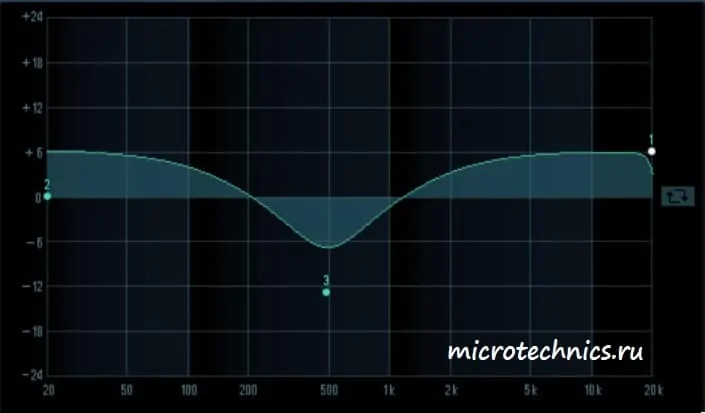
Во втором случае ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
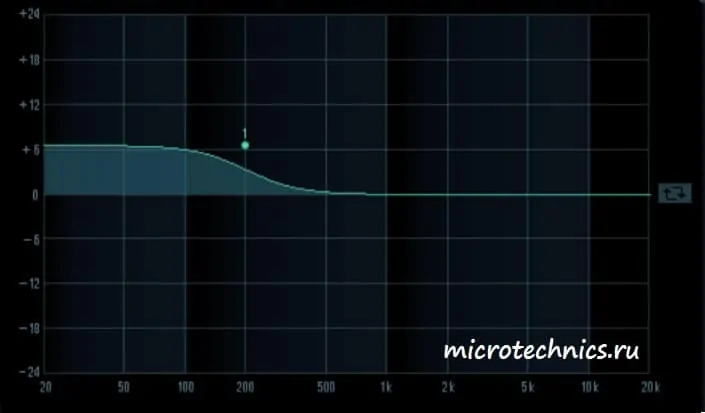
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.
На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝
Преобразование Фурье в действии: точное определение частоты сигнала и выделение нот
Время на прочтение
12 мин
Количество просмотров 225K
последняя редакция статьи доступна на сайте makeloft.xyz
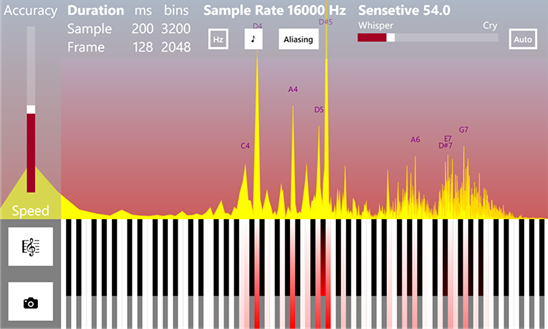
Начнём с пианино. Очень упрощёно этот музыкальный инструмент представляет собой набор белых и чёрных клавиш, при нажатии на каждую из которых извлекается определённый звук заранее заданной частоты от низкого до высокого. Конечно, каждый клавишный инструмент имеет свою уникальную тембральную окраску звучания, благодаря которой мы можем отличить, например, аккордеон от фортепиано, но если грубо обобщить, то каждая клавиша представляет собой просто генератор синусоидальных акустических волн определённой частоты.
Когда музыкант играет композицию, то он поочерёдно или одновременно зажимает и отпускает клавиши, в результате чего несколько синусоидальных сигналов накладываются друг на друга образуя рисунок. Именно этот рисунок воспринимается нами как мелодия, благодаря чему мы без труда узнаём одно произведение, исполняемое на различных инструментах в разных жанрах или даже непрофессионально напеваемое человеком.
Наглядная иллюстрация нотного рисунка
Определение частоты (режим гитарного тюнера)
Обратная задача состоит в том, чтобы разобрать звучащую музыкальную композицию на ноты. То есть разложить суммарный акустический сигнал, улавливаемый ухом, на исходные синусоиды. По сути, этот процесс и представляет собой прямое преобразование Фурье. А нажатие на клавиши и извлечение звука есть процесс обратного преобразования Фурье.
Математически в первом случае происходит разложение сложной периодической (на некотором временном интервале) функции в ряд более элементарных ортогональных функций (синусоид и косинусоид). А во втором их обратное суммирование, то есть синтез сложного сигнала.
Ортогональность, в некотором роде, обозначает несмешиваемость функций. Например, если мы возьмём несколько кусочков цветного пластилина и склеим их, то потом всё же сможем разобрать, какие цвета были изначально, но если хорошенько перемешаем несколько баночек гуашевых красок, то точно восстановить исходные цвета без дополнительной информации уже будет невозможно.
(!) Важно понимать, когда мы берёмся анализировать реальный сигнал с помощью преобразования Фурье, мы идеализируем ситуацию и исходим из предположения, что он периодический на текущем временном интервале и состоит из элементарных синусоид. Зачастую это именно так, поскольку акустические сигналы, как правило, имеют гармоническую природу, но вообще возможны и более сложные случаи. Любые наши допущения о природе сигнала обычно ведут к частичным искажениям и погрешностям, но без этого выделить полезную информацию из него крайне сложно.
Теперь опишем весь процесс анализа более подробно:
1. Всё начинается с того, что звуковые волны колеблют мембрану микрофона, который преобразует их в аналоговые колебания электрического тока.
2. Затем происходит дискретизация аналогового электрического сигнала в цифровую форму. На этом моменте стоит остановиться подробно.
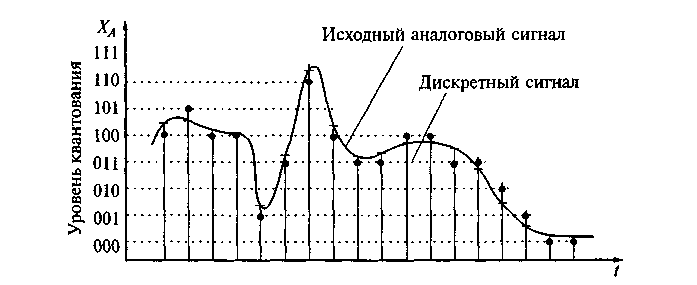
Поскольку аналоговый сигнал математически состоит из бесконечного непрерывного во времени множества точек-значений амплитуды, в процессе измерения мы можем выделить из него лишь конечный ряд значений в дискретные моменты времени, то есть, по сути, выполнить квантование по времени…
Как правило, значения-отсчёты берутся через небольшие равные временные промежутки, то есть с определённой частотой, например, 16000 или 22000 Гц. Однако в общем случае дискретные отсчёты могут идти и неравномерно, но это усложняет математический аппарат анализа, поэтому на практике обычно не применяется.
Существует важная теорема Котельникова-Найквиста-Шеннона, которая гласит, что аналоговый периодический сигнал, имеющий конечный (ограниченный по ширине) спектр, может быть однозначно восстановлен без искажений и потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте спектра (называемой частотой дискретизации или Найквиста).
Для этого восстановления необходимо применить специальные интерполирующие функции, но проблема в том, что при использовании данных функций вычисления нужно выполнять на бесконечном временном интервале, что на практике невозможно. Поэтому в реальной жизни нельзя сколь угодно повысить частоту дискретизации искусственным образом без искажений даже если изначально она удовлетворяет теореме Котельникова-Найквиста-Шеннона. Для этой операции применяются фильтры Фарроу.
Также дискретизация происходит не только по времени, но и по уровню значений амплитуды, поскольку компьютер способен манипулировать лишь ограниченным множеством чисел. Это также вносит небольшие погрешности.
3. На следующем этапе происходит само дискретное прямое преобразование Фурье.
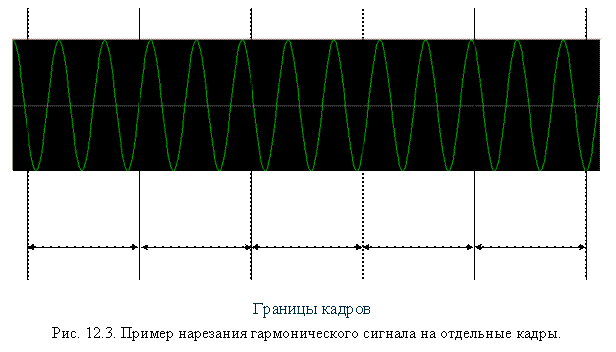
Мы выделяем короткий кадр (интервал) композиции, состоящий из дискретных отсчётов, который условно считаем периодическим и применяем к нему преобразование Фурье. В результате преобразования получаем массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах анализируемого кадра. Причём спектры также являются дискретными с шагом равным (частота дискретизации)/(количество отсчётов). То есть чем больше мы берём отсчётов, тем более точное разрешение получаем по частоте. Однако при постоянной частоте дискретизации увеличивая число отсчётов, мы увеличиваем анализируемый временной интервал, а поскольку в реальных музыкальных произведениях ноты имеют различную длительность звучания и могут быстро сменять друг друга, происходит их наложение, поэтому амплитуда длительных нот «затмевает» собой амплитуду коротких. С другой стороны для гитарных тюнеров такой способ увеличения разрешения по частоте подходит хорошо, поскольку нота, как правило, звучит долго и одна.
Существует также довольно простой трюк для увеличения разрешения по частоте — нужно исходный дискретный сигнал заполнить нулями между отсчётами. Однако в результате такого заполнения сильно искажается фазовый спектр, но зато увеличивается разрешение амплитудного. Также возможно применение фильтров Фарроу и искусственное увеличение частоты дискретизации, однако и оно вносит искажения в спектры.
Длительность кадра обычно составляет приблизительно от 30 мс до 1 с. Чем он короче, тем лучшее разрешение мы получаем по времени, но худшее по частоте, чем сэмпл длиннее, тем лучшее по частоте, но худшее по времени. Это очень напоминает принцип неопределённости Гейзенберга из квантовой механики..и не с проста, как гласит Википедия, соотношение неопределенностей в квантовой механике в математическом смысле есть прямое следствие свойств преобразования Фурье…
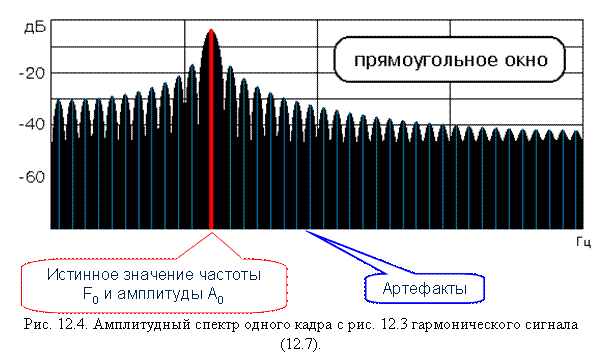
Интересно и то, что в результате анализа сэмпла одиночного синусоидального сигнала амплитудный спектр очень напоминает дифракционную картинку…
Синусоидальный сигнал, ограниченный прямоугольным окном, и его «дифракция»
Дифракция световых волн
На практике это нежелательный эффект, затрудняющий анализ сигналов, поэтому его стараются понизить путём применения оконных функций. Таких функций придумано немало, ниже представлены реализации некоторых из них, а также сравнительное влияние на спектр одиночного синусоидального сигнала.
Применяется оконная функция ко входному кадру очень просто:
for (var i = 0; i < frameSize; i++)
{
frame[i] *= Window.Gausse(i, frameSize);
}
using System;
using System.Numerics;
namespace Rainbow
{
public class Window
{
private const double Q = 0.5;
public static double Rectangle(double n, double frameSize)
{
return 1;
}
public static double Gausse(double n, double frameSize)
{
var a = (frameSize - 1)/2;
var t = (n - a)/(Q*a);
t = t*t;
return Math.Exp(-t/2);
}
public static double Hamming(double n, double frameSize)
{
return 0.54 - 0.46*Math.Cos((2*Math.PI*n)/(frameSize - 1));
}
public static double Hann(double n, double frameSize)
{
return 0.5*(1 - Math.Cos((2*Math.PI*n)/(frameSize - 1)));
}
public static double BlackmannHarris(double n, double frameSize)
{
return 0.35875 - (0.48829*Math.Cos((2*Math.PI*n)/(frameSize - 1))) +
(0.14128*Math.Cos((4*Math.PI*n)/(frameSize - 1))) - (0.01168*Math.Cos((4*Math.PI*n)/(frameSize - 1)));
}
}
}
Что касается компьютеров, в своё время был разработан алгоритм быстрого преобразования Фурье, который минимизирует число математических операций, необходимых для его вычисления. Единственное требование алгоритма состоит в том, чтобы число отсчётов было кратно степени двойки (256, 512, 1024 и так далее).
Ниже его классическая рекурсивная реализация на языке C#.
using System;
using System.Numerics;
namespace Rainbow
{
public static class Butterfly
{
public const double SinglePi = Math.PI;
public const double DoublePi = 2*Math.PI;
public static Complex[] DecimationInTime(Complex[] frame, bool direct)
{
if (frame.Length == 1) return frame;
var frameHalfSize = frame.Length >> 1; // frame.Length/2
var frameFullSize = frame.Length;
var frameOdd = new Complex[frameHalfSize];
var frameEven = new Complex[frameHalfSize];
for (var i = 0; i < frameHalfSize; i++)
{
var j = i << 1; // i = 2*j;
frameOdd[i] = frame[j + 1];
frameEven[i] = frame[j];
}
var spectrumOdd = DecimationInTime(frameOdd, direct);
var spectrumEven = DecimationInTime(frameEven, direct);
var arg = direct ? -DoublePi/frameFullSize : DoublePi/frameFullSize;
var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg));
var omega = Complex.One;
var spectrum = new Complex[frameFullSize];
for (var j = 0; j < frameHalfSize; j++)
{
spectrum[j] = spectrumEven[j] + omega*spectrumOdd[j];
spectrum[j + frameHalfSize] = spectrumEven[j] - omega*spectrumOdd[j];
omega *= omegaPowBase;
}
return spectrum;
}
public static Complex[] DecimationInFrequency(Complex[] frame, bool direct)
{
if (frame.Length == 1) return frame;
var halfSampleSize = frame.Length >> 1; // frame.Length/2
var fullSampleSize = frame.Length;
var arg = direct ? -DoublePi/fullSampleSize : DoublePi/fullSampleSize;
var omegaPowBase = new Complex(Math.Cos(arg), Math.Sin(arg));
var omega = Complex.One;
var spectrum = new Complex[fullSampleSize];
for (var j = 0; j < halfSampleSize; j++)
{
spectrum[j] = frame[j] + frame[j + halfSampleSize];
spectrum[j + halfSampleSize] = omega*(frame[j] - frame[j + halfSampleSize]);
omega *= omegaPowBase;
}
var yTop = new Complex[halfSampleSize];
var yBottom = new Complex[halfSampleSize];
for (var i = 0; i < halfSampleSize; i++)
{
yTop[i] = spectrum[i];
yBottom[i] = spectrum[i + halfSampleSize];
}
yTop = DecimationInFrequency(yTop, direct);
yBottom = DecimationInFrequency(yBottom, direct);
for (var i = 0; i < halfSampleSize; i++)
{
var j = i << 1; // i = 2*j;
spectrum[j] = yTop[i];
spectrum[j + 1] = yBottom[i];
}
return spectrum;
}
}
}
Существует две разновидности алгоритма БПФ — с прореживанием по времени и по частоте, но оба дают идентичный результат. Функции принимают массив комплексных чисел, заполненный реальными значениями амплитуд сигнала во временной области, а после своего выполнения возвращают массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах. Стоит помнить, что реальная и мнимая части комплексного числа — это далеко не то же самое, что его амплитуда и фаза!
magnitude = Math.Sqrt(x.Real*x.Real + x.Imaginary*x.Imaginary)
phase = Math.Atan2(x.Imaginary, x.Real)
Результирующий массив комплексных чисел заполнен полезной информацией ровно на половину, другая половина является лишь зеркальным отражением первой и спокойно может быть исключена из рассмотрения. Если вдуматься, то этот момент хорошо иллюстрирует теорему Котельникова-Найквиста-Шеннона, о том, что частота дискретизации должна быть не меньше максимальной удвоенной частоты сигнала…
Также существует разновидность алгоритма БПФ без рекурсии по Кули-Тьюки, которая часто применяется на практике, но она чуть более сложна для восприятия.
Сразу после вычисления преобразования Фурье удобно нормализовать амплитудный спектр:
var spectrum = Butterfly.DecimationInTime(frame, true);
for (var i = 0; i < frameSize; i++)
{
spectrum[i] /= frameSize;
}
Это приведёт к тому, что величина значений амплитуды получится одного порядка не зависимо от размеров сэмпла.
Вычислив амплитудный и частотный спектры, легко производить обработку сигнала, например, применять частотную фильтрацию или производить сжатие. По сути, таким образом можно сделать эквалайзер: выполнив прямое преобразование Фурье, легко увеличить или уменьшить амплитуду определённой области частот, после чего выполнить обратное преобразование Фурье (хотя работа настоящих эквалайзеров обычно основана на другом принципе — фазовом сдвиге сигнала). Да и сжать сигнал очень просто — нужно всего лишь сделать словарь, где ключом является частота, а значением соответствующее комплексное число. В словарь нужно занести лишь те частоты, амплитуда сигнала на которых превышает какой-то минимальный порог. Информация о «тихих» частотах, не слышимых ухом, будет потеряна, но получится ощутимое сжатие при сохранении приемлемого качества звучания. Отчасти этот принцип лежит в основе многих кодеков.
4. Точное определение частоты
Дискретное преобразование Фурье даёт нам дискретный спектр, где каждое значение амплитуды отстоит от соседних на равные промежутки по частоте. И если частота в сигнале кратна шагу равному (частота дискретизации)/(количество отсчётов), то мы получим выраженный остроконечный пик, но если частота сигнала лежит где-то между границами шага ближе к середине у нас выйдет пик со «срезанной» вершиной и нам будет затруднительно сказать, что же там за частота. Очень может быть что в сигнале присутствуют две частоты лежащие рядом друг с другом. В этом и заключается ограничение разрешения по частоте. Так же как на фотоснимке с низким разрешением мелкие предметы склеиваются и становятся неразличимы, так же и тонкие детали спектра могут теряться.
Но частоты музыкальных нот лежат далеко не на сетке шагов преобразования Фурье, а для повседневных задач настройки музыкальных инструментов и распознавания нот необходимо знать именно точную частоту. Более того, на низких октавах при разрешении от 1024 отсчётов и ниже сетка частот Фурье становится настолько редкой, что попросту на одном шаге начинают умещаться несколько нот и определить какая же на самом деле из них играет становится фактически невозможно.
Чтобы как-то обойти это ограничение иногда применяют аппроксимирующие функции, например, параболические.
www.ingelec.uns.edu.ar/pds2803/Materiales/Articulos/AnalisisFrecuencial/04205098.pdf
mgasior.web.cern.ch/mgasior/pap/biw2004_poster.pdf
Но всё это искусственные меры, которые улучшая одни показатели могут давать искажения в других.
Существует ли более естественный путь для точного определения частоты?
Да, и скрыт он как раз-таки в использовании фазового спектра сигнала, которым часто пренебрегают.
Данный метод уточнения частоты сигнала, основан на вычислении задержки фаз у спектров двух кадров, наложенных друг на друга, но немного сдвинутых во времени.
Подробно прочитать о нём можно по ссылкам:
www.guitarpitchshifter.com/algorithm.html
www.dspdimension.com/admin/pitch-shifting-using-the-ft (+ примеры кода)
eudl.eu/pdf/10.1007/978-3-642-29157-9_43
ctuner.googlecode.com (примеры использования алгоритма на C++ и Java)
На C# реализация метода выглядит довольно просто:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
namespace Rainbow
{
// Δ∂ωπ
public static class Filters
{
public const double SinglePi = Math.PI;
public const double DoublePi = 2*Math.PI;
public static Dictionary<double, double> GetJoinedSpectrum(
IList<Complex> spectrum0, IList<Complex> spectrum1,
double shiftsPerFrame, double sampleRate)
{
var frameSize = spectrum0.Count;
var frameTime = frameSize/sampleRate;
var shiftTime = frameTime/shiftsPerFrame;
var binToFrequancy = sampleRate/frameSize;
var dictionary = new Dictionary<double, double>();
for (var bin = 0; bin < frameSize; bin++)
{
var omegaExpected = DoublePi*(bin*binToFrequancy); // ω=2πf
var omegaActual = (spectrum1[bin].Phase - spectrum0[bin].Phase)/shiftTime; // ω=∂φ/∂t
var omegaDelta = Align(omegaActual - omegaExpected, DoublePi); // Δω=(∂ω + π)%2π - π
var binDelta = omegaDelta/(DoublePi*binToFrequancy);
var frequancyActual = (bin + binDelta)*binToFrequancy;
var magnitude = spectrum1[bin].Magnitude + spectrum0[bin].Magnitude;
dictionary.Add(frequancyActual, magnitude*(0.5 + Math.Abs(binDelta)));
}
return dictionary;
}
public static double Align(double angle, double period)
{
var qpd = (int) (angle/period);
if (qpd >= 0) qpd += qpd & 1;
else qpd -= qpd & 1;
angle -= period*qpd;
return angle;
}
}
}
Применение также несложное:
var spectrum0 = Butterfly.DecimationInTime(frame0, true);
var spectrum1 = Butterfly.DecimationInTime(frame1, true);
for (var i = 0; i < frameSize; i++)
{
spectrum0[i] /= frameSize;
spectrum1[i] /= frameSize;
}
var spectrum = Filters.GetJoinedSpectrum(spectrum0, spectrum1, ShiftsPerFrame, Device.SampleRate);
Обычно исходные кадры сдвинуты на 1/16 или 1/32 своей длины, то есть ShiftsPerFrame равно 16 или 32.
В результате мы получим словарь частота-амплитуда, где значения частот будут довольно близки к реальным. Однако «срезанные пики» всё ещё будут наблюдаться, хоть и менее выражено. Чтобы устранить этот недостаток, можно просто «дорисовать» их.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
namespace Rainbow
{
public static class Filters
{
public static Dictionary<double, double> Antialiasing(Dictionary<double, double> spectrum)
{
var result = new Dictionary<double, double>();
var data = spectrum.ToList();
for (var j = 0; j < spectrum.Count - 4; j++)
{
var i = j;
var x0 = data[i].Key;
var x1 = data[i + 1].Key;
var y0 = data[i].Value;
var y1 = data[i + 1].Value;
var a = (y1 - y0)/(x1 - x0);
var b = y0 - a*x0;
i += 2;
var u0 = data[i].Key;
var u1 = data[i + 1].Key;
var v0 = data[i].Value;
var v1 = data[i + 1].Value;
var c = (v1 - v0)/(u1 - u0);
var d = v0 - c*u0;
var x = (d - b)/(a - c);
var y = (a*d - b*c)/(a - c);
if (y > y0 && y > y1 && y > v0 && y > v1 &&
x > x0 && x > x1 && x < u0 && x < u1)
{
result.Add(x1, y1);
result.Add(x, y);
}
else
{
result.Add(x1, y1);
}
}
return result;
}
}
}
Перспективы
Нотный анализ музыкальных произведений открывает ряд интересных возможностей. Ведь имея в наличии готовый нотный рисунок, можно осуществлять поиск других музыкальных композиций со схожим рисунком.
Например, одно и то же произведение может быть исполнено на другом инструменте, в различной манере, с другим тембром, либо транспонировано по октавам, однако нотный рисунок останется похожим, что позволит найти различные варианты исполнения одного и того же произведения. Это очень напоминает игру «угадай мелодию».
В некоторых случаях подобный анализ поможет выявить плагиат в музыкальных произведениях. Также по нотному рисунку, теоретически, можно искать произведения определённого настроения или жанра, что поднимает поиск на новый уровень.
Итоги
В этой статье изложены основные принципы точного определения частот акустических сигналов и выделения нот. А также показана некоторая тонкая интуитивная связь дискретного преобразования Фурье с квантовой физикой, что подталкивает на размышления о единой картине мира.
P.S. Радужный фреймворк (Rainbow Framework) содержащий все вышеизложенные примеры кода можно скачать с Кодплекса.
P.P.S. Возможно, эта статья когда-нибудь серьёзно пригодится вам в профессиональной деятельности и поможет сохранить уйму времени и сил, поэтому если вы желаете отблагодарить автора за труд, то можете сделать пожертвование, купить приложение (бесплатная версия с рекламой), благодаря которому статья возникла, либо просто выразить благодарность добрым словом.
Литература
1. Основы спектрального анализа звуков pandia.org/text/77/481/644.php
2. Алгоритм Кули-Тьюки www.codeproject.com/Articles/32172/FFT-Guitar-Tuner
3. Передискретизация (ресэмплинг)
www.dsplib.ru/forum/viewtopic.php?f=5&t=11
www.dsplib.ru/content/farrow/farrow.html
4. Коррекция частоты по смещению фазы
www.guitarpitchshifter.com/algorithm.html
www.dspdimension.com/admin/pitch-shifting-using-the-ft (+ примеры кода)
eudl.eu/pdf/10.1007/978-3-642-29157-9_43
ctuner.googlecode.com (примеры использования алгоритма на C++ и Java)