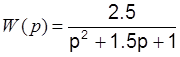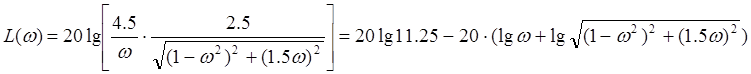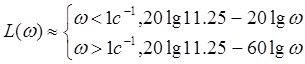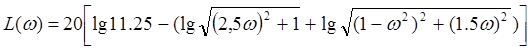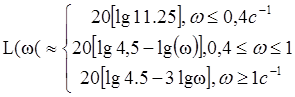Как найти частоту сопряжения - Исправление недочетов и поиск решений вместе с Examum.ru

Перейти к содержимому

Частота среза — частота, на которой частотная характеристика пересекает 0 дБ.

Частота сопряжения — частота, на которой частотная характеристика меняет наклон.

Эти понятия относятся к теории автоматического управления. Частота среза используется при анализе устойчивости системы управления. Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы фаза разомкнутой системы не достигала −180° на частоте среза.

Частота среза имеет другое определение в обработке сигналов. Там под частотой среза подразумевают частоту сопряжения, а понятием частота сопряжения не пользуются. В обработке сигналов нет необходимости анализировать устойчивость системы.

Понятия раскрываются в книге Бесекерского и Попова «Теория систем автоматического регулирования» 2003 года. Приведу пару цитат, где вводятся эти понятия.

Первая цитата со страницы 59:

Точку пересечения прямой с осью нуля децибел (осью частот) можно найти, положив L(ω)=0 или, соответственно, A(ω)=1. Отсюда получаем так называемую частоту среза л. а. х.,

При этом в книге частота среза обозначается как ω_ср.

На странице 66 описывается апериодическое звено первого порядка:

Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая л. а. х. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой ω=1/T.

При чем эта «вертикальная прямая» проводится в точке изменения наклона частотной характеристики.

Скриншот этой страницы с полным описанием:

Источник

Как
было показано в п. 3.2.1, передаточные и
частотные функции последовательно
соединенных звеньев перемножаются, а
их логарифмические характеристики —
складываются, т.е.

,
,,

,
.

Отсюда
вытекает правило построения ЛАЧХ и ЛФЧХ
разомкнутой одноконтурной САУ: строят
логарифмические характеристики звеньев
и затем их графически складывают.

Но
для построения асимптотической ЛАЧХ
применяют более простой метод, который
сформулируем после рассмотрения
конкретного примера.

Пример
4.6

Построить
асимптотическую ЛАЧХ для разомкнутой
цепи САУ с передаточной функцией

где
,с,с,с.

По
виду передаточной функции можно
заключить, что система состоит из
последовательно соединенных интегрирующего,
форсирующего, инерционного звеньев и
звена второго порядка.

Определим,
каким является звено второго порядка,
рассчитав его коэффициент демпфирования:

Поскольку
,
звено второго порядка является
колебательным.

Рассчитаем
частоты сопряжения по соотношению
,
где— постоянная времени-го
звена:

,
,,

где

— частота сопряжения инерционного
звена,— частота сопряжения форсирующего
звена,— частота сопряжения колебательного
звена.

Соответственно
логарифмы частот сопряжения равны

дек,
,дек.

Будем
считать, что коэффициент передачи
интегрирующего звена равен коэффициенту
передачи разомкнутой цепи САУ, а
коэффициенты передачи всех остальных
звеньев равны единице. Определим величину
дБ.

На
рис. 4.15 показан процесс построения
асимптотической ЛАЧХ разомкнутой цепи
САУ.

Характеристики
звеньев построены на рис. 4.15, где
соответственно ломаные линии 1, 2, 3, 4
являются ЛАЧХ интегрирующего, инерционного,
форсирующего и колебательного звеньев.
Так как коэффициенты передачи всех
звеньев, кроме интегрирующего, приняты
единичными, то ЛАЧХ этих звеньев при
совпадают с осью частот.

Просуммировав
графически ЛАЧХ всех звеньев, получим
характеристику 5, являющуюся асимптотической
ЛАЧХ разомкнутой цепи САУ.

Из
этого примера видно, что суммарную
характеристику легко можно построить,
не изображая характеристик отдельных
звеньев. Поэтому при построении ЛАЧХ
разомкнутых САУ вначале проводят первую
асимптоту через точку с координатами
с наклоном,
гдеравно разности между числами идеальных
интегрирующих и дифференцирующих
звеньев. После каждой сопрягающей
частоты наклон ЛАЧХ изменяют, причем
изменение наклона определяется типом
звена, давшим сопрягающую частоту.
Причем если у колебательного звена <
0,4, на соответствующей частоте необходимо
изобразить «горб» в соответствии с
величиной .

Рис.
4.15 — Построение асимптотической ЛАЧХ
разомкнутой цепи

Возможно
и решение обратной задачи — восстановление
передаточной функции по ее асимптотической
ЛАЧХ.

Пример
4.7.

По
заданной на рис. 4.16 асимптотической
ЛАЧХ одноконтурной разомкнутой системы
требуется восстановить ее передаточную
функцию.

Рис.
4.16 — Восстановление передаточной
функции по

асимптотической
ЛАЧХ

Величина
наклона первой асимптоты (по мере роста
частоты) указывает на присутствие в
структуре системы интегрирующего звена.

Для
первой асимптоты поэтому справедливо
уравнение (см. характеристики интегрирующего
звена):
.

Определить
параметр
можно, отсчитав с графика координаты
любой точки этой асимптоты. Например

,
,,.

После
первой по величине частоты сопряжения
наклон ЛАЧХ изменился на плюс 20 дБ/дек.
Такой наклон имеет ЛАЧХ форсирующего
звена. Следовательно, в структуре системы
есть форсирующее звено. Анализируя
изменение наклонов асимптот ЛАЧХ можно
заключить, что помимо упомянутых типовых
звеньев в систему включены колебательное
звено, еще одно форсирующее и инерционное
звенья.

В
общем виде передаточная функция будет
следующей:

По
частотам сопряжения рассчитаем
соответствующие постоянные времени:

;
;с;

;
;с.

По
всплеску ЛАЧХ на частоте сопряжения
колебательного звена определим
коэффициент демпфирования:

Окончательный
ответ:

Следует
отметить, что восстановление передаточной
функции САУ по асимптотической ЛАЧХ
возможно в том случае, если система
содержит только минимально-фазовые
звенья. Если же в ней имеются особые
звенья (неминимально-фазовые,
иррациональные, звенья чистого
запаздывания), эта задача не имеет
однозначного решения, т.к. асимптотические
ЛАЧХ этих звеньев такие же, как и у
минимально-фазовых звеньев (см. подраздел
3.3).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Reading time
4 min

Views 4.9K

В других сериях:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (РЕГУЛИРОВАНИЯ).
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ.
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
3.3. Апериодическое звено 1–го порядка (инерционное звено). На примере входной камеры ядерного реактора.
3.4. Апериодическое звено 2-го порядка.
3.5 Колебательное звено.
3.7. Форсирующие звено.

Тема сегодняшней статьи: 3.6. Инерционно-дифференцирующее звено

В качестве примера инерционно-дифференцирующего звена рассмотрим электрическую схему приведенную на рисунке 3.6.0, в которой входным воздейстиве является напряжение источника $U_{вх}(t)$ , а выходом явяляется напряжение на резисторе $U_R=U_{вых}$ .

Рисунок 3.6.0 Электрическая схема инерционно-дифференцирующего звена

Согласно второму закону Кирхгофа для замкнутого контура, сумма Э.Д.С равна сумме напряжения на резистивных элементах контура:

$U_{вх} = U_R+U_C$

где: — напряжение на резисторе;

Ток в замкнутом контуре одинаковый на всех элементах, запишем выражение для силы тока на конденсаторе: $I = frac{dq_c}{dt}$ ;

где: — заряд на конденсаторе; Выразим напряжение на конденсаторе через входное напряжения и напряжения на резисторе: $U_c = U_{вх}-U_R$ , и подставим в выражение второго закона Киргофа:

$U_{вх}=underbrace{С cdot frac{d(U_{вх}-U_R)}{dt}cdot R}_{U_R=I cdot R} +underbrace{U_{вх}-U_{R}}_{U_c} Rightarrow$ $U_{вх} = C cdot R cdot frac{dU_{вх}}{dt} - C cdot R cdot frac{dU_R}{dt}+ U_{вх}-U_R Rightarrow$ $Ccdot R cdot frac{d U_{R}}{dt}+U_R = C cdot R cdot frac{dU_{вх}}{dt}$

заменяя на привычные и $x(t) = U_{ВХ}$ получим уравнение звена в классической форме:

$underbrace{Ccdot R}_T cdot y'(t)+y(t) = underbrace{C cdot R}_tau cdot x(t)$

Посмотрим какая размерность у нас получилась в коффициентах:

$[Сcdot R]= [Ф cdot ОМ] = left[frac{A^2 cdot c^4}{кг cdot м^2} cdot frac{кг cdot м^2}{A^2 cdot c^3} right] =[c]$

Мы видим, что несмотя на то, что у нас используются электрические единицы измерения, мы опять в коэффициентах уравнениях динамики пришли к размерность времени — секунды. Так же как для уравнений динамики груза на пружинке, где использовались законы мехники. (см. раздел 2.1)

Уравнение динамики инерционно-дифференцирующего звена имеет вид:

иногда в выражении уравнения динамики и соотвественно звена, используется обозначение вместо обозначение tau , т.е. ;

Перейдем к изображением , ,, уравниние динамики в изображения Лапласа:

Передаточная функция звена:

$W(s) = frac{tau cdot s}{Tcdot s+1} mathbf{(3.6.3)}$

Выражение для АФЧХ получается после подстановки в (3.6.3) значения :

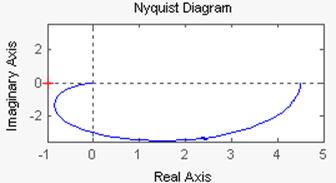
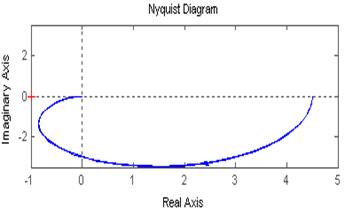
$W(s)_{s rightarrow i cdot omega} =frac{ tau cdot i cdot omega}{T cdot i cdot omega+1} = frac{tau cdot i cdot omega cdot (1- Tcdot icdot omega)}{1+T^2cdot omega^2} =\ underbrace{frac{tau cdot Tcdot omega^2}{1+T^2 cdot omega^2}}_{Re}+i cdot underbrace{frac{tau cdot omega}{1+T^2 cdot omega^2}}_{Im}$ $U(omega) = frac{tau cdot Tcdot omega^2}{1+T^2cdot omega^2}; V(omega) = frac{taucdotomega} {1+T^2 cdot omega^2}.$ $omega rightarrow 0 Rightarrow left { begin{gathered} u(omega) rightarrow 0 \ v(omega) rightarrow 0 end {gathered} right. ; omega rightarrow infty Rightarrow left { begin{gathered} u(omega) rightarrow tau/T \ v(omega) rightarrow 0 end {gathered} right. .$

Легко видеть, что годограф этого звена – полукруг (см. рисунок 3.6.2)

Рисунок 3.6.2 Годограф АФЧХ инерционно-дифференцирующего звена

Модуль АФЧХ определяется по формуле:

$A(omega) =sqrt{U(omega)^2+V(omega)^2}= frac{tau cdotomega}{sqrt{1+T^2 cdot omega} } mathbf{(3.6.5)}$

Cдвиг фазы определяется по формуле:

$phi(omega)= arctgfrac{V(omega)}{U(omega)} =arctg frac{1}{Tcdot omega} = arcctg (T cdot omega) mathbf{(3.6.6)}$

Логрифмическая амплитундая характеристика ЛАХ определяется по формуле:

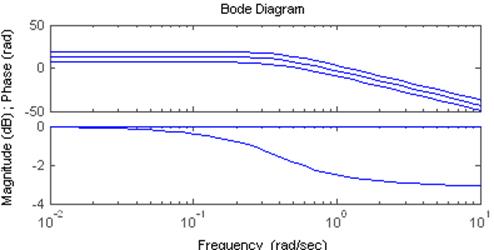
$Lm(omega) = 20 cdot lg(tau cdot omega) - 20 cdot lg sqrt{1+T^2cdot omega^2} mathbf{(3.6.7)}$

Постороим графики соотвесвующих функций см рис. 3.6.3 и 3.6.4

Рисунок 3.6.3 АЧХ и ФЧХ инерционно-дифференцирующего звена

Рисунок 3.6.4 ЛАХ и ЛФЧХ инерционно-дифференцирующего звена

Для инерционно-дифференцирующего звена частота сопряжения: $omega_{сопр} = 1/T;$

частота среза: $omega_{срез}= frac{1}{sqrt{tau^2-T^2}}$ , если tau>>T , то $omega_{среза} approx frac{1}{tau}.$

Анализируя поведение ЛАХ можно сказать что:

Если $omega <<frac{1}{T}$ — звено ведет себя как идеальное дифференцирующее

если $omega >> frac{1}{T}$ — звено ведет себя как идеальное усиливающие звено $W(s) approx frac{tau}{T}$ .

Переходная функция

$h(t) = L^{-1} left [ Н(s) right ]=L^{-1} left[ frac{W(s)}{s} right] = L^{-1} left[ frac{tau cdot s }{(Tcdot s+1) cdot s}right] =frac{tau}{T}L^{-1} left[frac{1}{s+frac{1}{T}} right]$ $h(t)=frac{tau}{T}cdot e^{-frac{t}{T}}cdot 1(t) mathbf{(3.6.8)}$

где 1(t) — единичная функция обеспечивающая h(0) =0 .

Рисунок 3.6.5 Переходная функция инерционно-дифференцирующего звена

Весовая функция получается путем диференцирования по времени переходной функции:

$omega(t)= h'(t) = frac{tau}{T}cdot e^{-frac{t}{T}} cdotdelta(t)-frac{tau}{T^2}cdot e^{-frac{t}{T}}cdot1(t) mathbf{(3.6.9)}$

Рисунок 3.6.6 Весовая функция инерционно-дифференцирующего звена

Примерами инерционно-дифференцирующего звена является:

Пассивная RC- цепочка
Трансформатор
Пассивная RL-цепочка
Механически демпфер с пружиной

Пример 1

В качестве примера возьмем модель электрического контура, уравнения физики которого мы использовали для вывода дифференциального уравнения для инерционно-дифференцирующего звена. Сравним модель в виде расчётной электрической схемы и в виде стандартного блока «инерционно-дифференцирующего звена». (см. рис. 3.6.7)

Для электрической схемы мы используем блок «Гармонический анализатор», который обеспечивает тестовое воздействие в заданном диапазоне частот и осуществляет построение характеристик по отклику системы.

Для звена мы используем блок «Построение частотных характеристик», который осуществляет расчёт характеристик в начале или конце расчёта. Для линейных динамических объектов реализованные численные алгоритмы блока позволяют определять амплитудно-фазовые частотные характеристики напрямую, по общеизвестным формулам.

3.6.7 Расчетная схема контура с инерционно-дифференцирующим звеном

В качестве характеристик звена используем k и Т используем выражение , полученное в начале статьи.

3.6.8 Праметры инерционно-дифференуируюещго звена

Результаты моделирования для электрического контура представлены на рисунке 3.6.9. Результаты моделирования для звена представлены на рисунке 3.6.10.

3.6.9 Результат гармонического анализа электрического контура.

3.6.10 Результаты гармонического анализа звена

Сравнение графиков модели электрического контура и модели в виде одного звена показывает их практическое совпадение. На рис. 3.6.9 в правой верхней части приведена увеличенная часть графика выходного напряжения и выхода блока. Видно что синусойды совпадют.

Годограф, построенный для электрического контура, представляет собой круг, как и предсказывает теория. Диаметр круга годографа равен tau/T (см. рисунок 3.6.2). В случае рассмотренного электрического контура , соответственно . Что мы и наблюдаем на годографе (правый нижний график рис. 3.6.9).

Пример 2

В качестве второго примера инерционно-дифференцирующего звена рассмотрим R-L электрический контур, представленный на рисунке 3.6.11

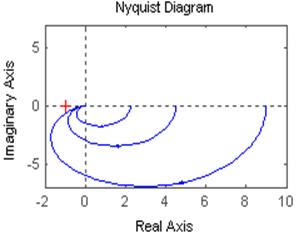
3.6.11 R-L цепь в качестве инерционно-диффернцируемого звена

Результат анализа (см. рис. 3.6.12) показывает, что данный конутр так же ведет себя как и предсказывает теория, годограф представлет собой круг, ЛАХ и ФЧХ выглядят так же.

3.6.12 Результаты гармонического анализа R-L цепочки.

Примеры для самостоятельного изучения можно взять здесь.

Предыдущая статья: 3.5. Колебательное звено.

Следующая статья: 3.7. Форсирующие звено.

Источник

Рассмотрим влияние на ЛАЧХ. Видно, что чем меньше частота
сопряжения, тем скорее ЛАЧХ приобретет наклон -20дБ/дек. Раньше всех перегнется
звено с ωсопр3=0,2 1/с, позже звено с ω1=0,8 1/с.

Рассмотрим влияние на ЛФЧХ.

Для ЛФЧХ точка перегиба также определяется частотой
сопряжения, чем больше частота сопряжения, тем позже происходит перегиб.

2.3 Колебательное
звено.

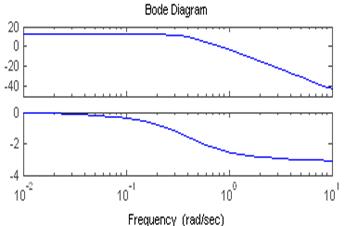
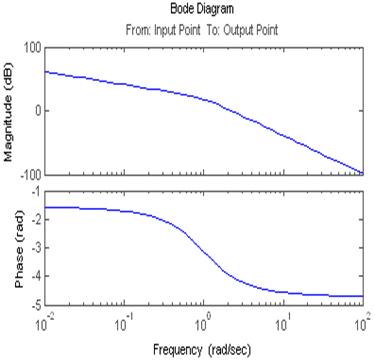
2.3.1. Постройте АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ для случая
колебательного звена с коэффициентом передачи k1,
постоянной времени Т1 и коэффициентом демпфирования ξ .

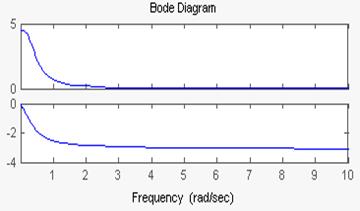
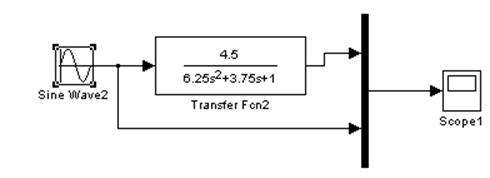
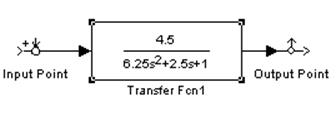
Передаточная функция этого звена 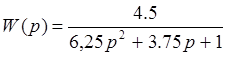ξ=0,75,
к=4,5, Т=2,5

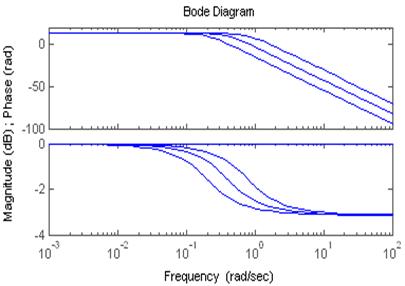
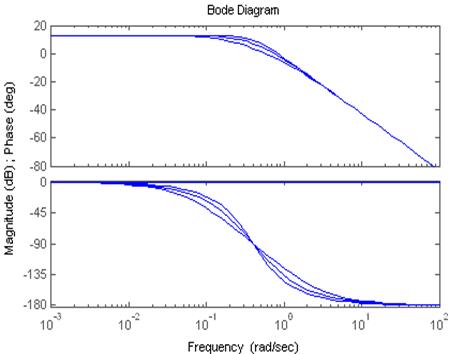
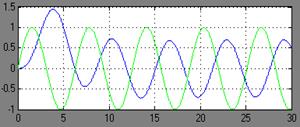
Слева представлены ЛАЧХ и ЛФЧХ, справа- АЧХ и ФЧХ.

2.3.2. По полученной АЧХ
получить параметры частотной характеристики.

1. Определим показатель колебательности Аmax(ω)=4.5
А(0)=4,5 М=4,5/4,5=1

2. Определим частоту среза: L(ωср)=0 → ωср=0,825 1/с

3.Полоса пропускания: →
полоса пропускания (0;0,376)

4. Резонансная частота ωрез=0 1/с.

2.3.3. Для трех частот, включая частоту сопряжения ,
экспериментально получите три точки АЧХ и ФЧХ и сравните полученные результаты
с с 2.3.1.

Из 2.3.1. получим, что

при ω1=1 А1(ω)=0,712 и φ1(ω)= -2,52рад.

При ω2=2 А2(ω)=0,182 и φ2(ω)= -2,84рад.

При ωсопр=0.4 Асопр(ω)=3 и φсопр(ω)=-1,57 рад

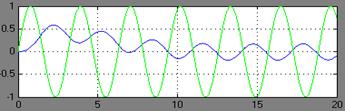
Теперь возьмем 3 гармонических воздействия одинаковой
амплитуды(Авх=1)и фазы (φвх=0), но разных частот и проследим какой будет Авых и
φвых.

ω=1

на выходе примерно Авых1(ω)=0,6973

φ1(ω)=0-2,5205=-2,5205рад.

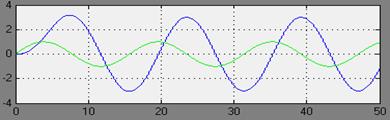
ω=2

на выходе примерно Авых2(ω)=0,1727
φ2(ω)=0-2*0,6867=-2,8824рад.

ω=0,4

на выходе примерно Авых.(ω)=
3 φвых3(ω)=0-0,4*3,9271=-1,57084рад.
результаты, полученные разными способами, почти не отличаются.

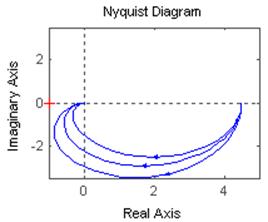
2.3.4. Постройте АФЧХ колебательного звена.

2.3.5 Исследуйте влияние коэффициента передачи k₁, постоянной времени T₁ и коэффициента демпфирования ξ колебательного
звена на ЛАЧХ, ЛФЧХ, АФЧХ при соблюдении следующих условий :

ξ=1, ξ>1, ξ<1

Сначала исследуем влияние коэффициента передачи k. k1=2.25,
k2=4,5, k3=9.

Для всех ξ=0,75 Т=2,5

На ЛФЧХ изменение k никак не влияет.

Рассмотрим влияние на ЛАЧХ. С увеличением k линии проходят выше, аналогично 2.2.4.

На рисунке с АФЧХ видно, что если ω=0

при к3=9 А(0)=9,

при к2=4,5 А(0)=4,5,

при к1=2,25 А(0)=2,25.

При одном и том же угле поворота А(ω) пропорционально
увеличилась, так как А(ω) линейно зависит от k,
а φ(ω) от k не зависит.

Теперь исследуем влияние Т:

T1=1,25 Т2=2,5 Т3=5. Для
всех к=4,5, ξ=0,75.

Рассмотрим влияние на ЛАЧХ.

Видно, что чем меньше частота сопряжения, тем скорее ЛАЧХ
приобретет наклон -20дБ/дек. Раньше всех перегнется звено с ωсопр3=0,2 1/с,
позже звено с ω1=0,8 1/с.

Рассмотрим влияние на ЛФЧХ.

АФЧХ для трех значений Т сливаются, но одна и та же точка
на АФЧХ соответствует трем разным частотам для трех разных Т, так как ВЧХ и МЧХ
зависят от Т*ω. Следовательно для достижения определенного значения МЧХ и ВЧХ
при большем Т требуется меньшее ω.

Исследуем влияние ξ:

ξ1=0,75, ξ2=1, ξ3=1,5. k=4.5
T=2.5

Влияние на ЛФЧХ.

Чем больше ξ, тем меньшее требуется ω для достижения
определенного уровня φ(ω)-до перегиба, а после- наоборот.

Влияние на ЛАЧХ.

Чем больше ξ, тем более плавно проходит кривая ЛАЧХ и тем
меньше значения L(ω) около частот сопряжения.

Чем меньше ξ, тем большие по модулю значения способны
принимать МЧХ и ВЧХ.

2.4. Частотные характеристики в логарифмическом
масштабе линейной одномерной непрерывной линейной САУ в разомкнутом состоянии.

2.4.1 Получите АЧХ и ФЧХ в логарифмическом масштабе
при последовательном соединении типовых интегрирующего и колебательного
звеньев.

Для интегрирующего звена 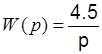, колебательного-

Построим ЛАЧХ..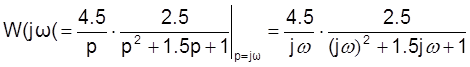

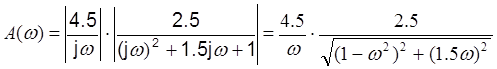
Из этой зависимости получим ωсопр=1
L(ωсопр)=21.023дБ

Экспериментально L(ωсопр)=17,5. Ошибка составляет
Δ=(21,023-17,5)/21,023*100%=16,75%

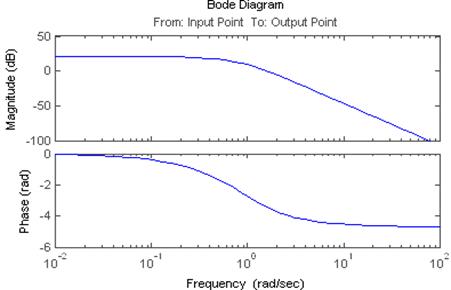
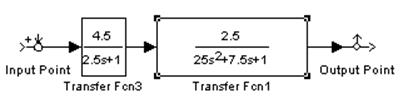
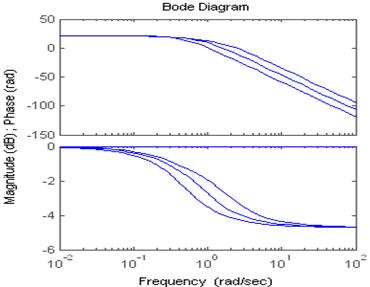
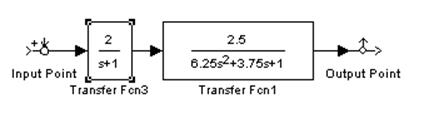
2.4.2. Постройте ЛАЧХ и ЛФЧХ последовательно
соединенных типовых апериодического и колебательного динамических звеньев.

Для апериодического звена ,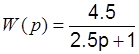

Построим ЛАЧХ..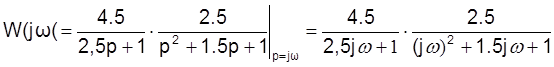

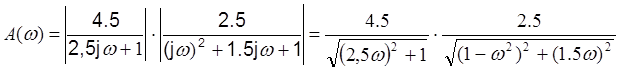
Из этой зависимости получим ωсопр1=0.4
L(ωсопр1)=21.023дБ;
ωсопр2=1 L(ωсопр2)=13.064дБ;

Экспериментально L(ωсопр1)=17,7. Ошибка составляет Δ=(21,023-17.7)/21,023*100%≈16%

L(ωсопр2)=8.74. Ошибка составляет Δ=(13.064-8.74)/13.064*100%=33%

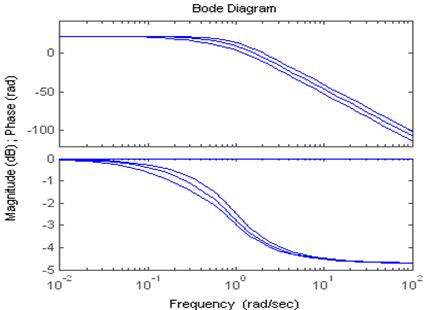
2.4.3. Исследуйте влияние коэффициента передачи САУ в
разомкнутом состоянии Краз, а так же постоянных времени апериодического и
колебательного звеньев на ЛАЧХ и ЛФЧХ для пункта 2.4.2.

Для рисунков слева меняемТ для апериодического звена,
справа- колебательного.

1.Изменяем Т для апериодического звена: Т1=2,5, Т2=1,25,
Т3=5.

С изменением Т меняется частота сопряжения
апериодического звена — для больших Т она меньше. Изменяется наклон между
частотами сопряжения, который определяется в основном Т апериодического звена,
так как ωсопр этого звена для всех случаев меньше ωсопр колебательного звена.

2. Изменяем Т для колебательного звена: Т1=1, Т2=0,5,
Т3=2. Изменяется частота сопряжения колебательного звена. Здесь для трех
случаев ωсопр этого звена всегда меньше ωсопр апериодического звена и,
следовательно, наклон между двумя этими частотами определяется Т колебательного
звена.

ЛФЧХ в этих случаях складываются перегибы наблюдаются в
φ(ω)=135гр.

Теперь коэффициент передачи:

k1=11.25; k2=22.5; k3=5.625

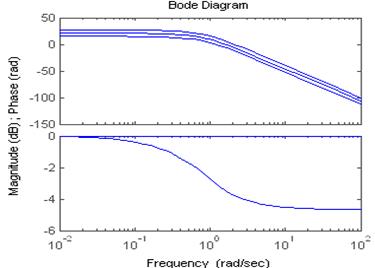
Изменение k никак не
влияет на ЛФЧХ, но с увеличением k линии ЛАЧХ
проходят выше.

При ω=0 L(ω)=20*lgk.

Вывод: на лабораторной работе мы исследовали с помощью
метода цифрового моделирования частотные характеристики типовых линейных
динамических звеньев в обычном и логарифмическом масштабах, а также строили
ЛАЧХ и ЛФЧХ одномерных линейных САУ в разомкнутом состоянии.

Источник