Загрузить PDF
Загрузить PDF
Частота (или частота волны) — это число полных колебаний или циклов волны, совершенных в единицу времени. Есть несколько различных способов вычислить частоту в зависимости от данной вам информации.
-
1
Формула: f = V / λ[1]
- где f — частота, V — скорость волны, λ — длина волны.
- Пример: вычислите частоту звуковой волны, если длина волны равна 322 нм, а скорость звука равна 320 м/сек.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.[2]
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 322 нм
- 322 нм x (1 м / 10^9 нм) = 3,22 x 10^-7 м = 0,000000322 м
-
3
Разделите скорость волны на ее длину. Для вычисления частоты (f) разделите скорость волны (V) на ее длину (λ), выраженную в метрах.[3]
- Пример: f = V / λ = 320 / 0.000000322 = 993788819,88 = 9,94 x 10^8
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 9,94 х 10^8 Гц.
Реклама
-
1
Формула: f = C / λ. Формула для вычисления частоты волны в вакууме практически идентична формуле для вычисления частоты волны в средах. В вакууме не существует факторов, влияющих на скорость волны, поэтому в формуле используется постоянная величина скорости света, с которой распространяются электромагнитные волны в вакууме.[4]
- В формуле f — частота, С — скорость света, λ — длина волны.
- Пример: вычислите частоту электромагнитной волны, если ее длина равна 573 нм.
-
2
Преобразуйте единицы измерения длины волны в метры (если необходимо). Если длина волны дается в нанометрах, вам нужно конвертировать это значение в метры, разделив его на количество нанометров в одном метре.
- Обратите внимание, что при работе с очень малыми или очень большими числами лучше записывать их в экспоненциальном формате. В этой статье числа будут даны как в обычном, так и в экспоненциальном формате.
- Пример: λ = 573 нм
- 573 нм х ( 1 м / 10^9 нм) = 5,73 х 10^-7 м = 0,000000573
-
3
Разделите скорость света на длину волны. Скорость света является постоянной величиной, которая равна 3,00 х 10^8 м/с. Разделите эту величину на длину волны (в метрах).[5]
- Пример: f = С / λ = 3,00 х 10^8 / 5,73 х 10^-7 = 5,24 х 10^14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота этой волны равна 5,24 х 10^14 Гц.
Реклама
-
1
Формула: f = 1 / T.[6]
Частота обратно пропорциональна времени, которое необходимо для совершения одного колебания волны.- В формуле f — частота, Т — время, которое необходимо для совершения одного колебания волны.
- Пример А: вычислите частоту волны, если ей необходимо 0,32 с для совершения одного колебания.
- Пример B: за 0,57 секунд волна совершает 15 колебаний. Вычислите частоту этой волны.
-
2
Разделите число колебаний на время. Если в задаче дано время, затрачиваемое на 1 колебание, то в этом случае просто разделите 1 на время (Т). Если в задаче дано время, затрачиваемое на несколько колебаний, то в этом случае разделите данное количество колебаний (n) на время (Т).[7]
- Пример А: f = 1 / T = 1 / 0,32 = 3,125
- Пример B : f = n / T = 15 / 0,57 = 26,316
-
3
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример А: частота волны равна 3,125 Гц.
- Пример B: частота волны равна 26,316 Гц.
Реклама
-
1
Формула: f = ω / (2π)[8]
- где f — частота, ω — угловая частота, π — число Пи (математическая константа).
- Пример: волна вращается с угловой частотой 7,17 радиан в секунду. Вычислите частоту этой волны.
-
2
Умножьте Пи на два.
- Пример: 2 * π = 2 * 3,14 = 6,28
-
3
Разделите угловую частоту (в радианах в секунду) на удвоенное число пи (6,28).[9]
- Пример: f = ω / (2π) = 7,17 / (2 * 3,14) = 7,17 / 6,28 = 1,14
-
4
Запишите ответ. Рядом поставьте единицу измерения частоты — Герц (Гц).
- Пример: частота волны равна 1,14 Гц.
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 114 081 раз.
Была ли эта статья полезной?
Download Article
Download Article
Frequency, also called wave frequency, is a measurement of the total number of vibrations or oscillations made within a certain amount of time. There are a few different ways to calculate frequency based on the information you have available to you. Keep reading to learn some of the most common and useful versions.
-
1
Learn the formula. The formula for frequency, when given wavelength and the velocity of the wave, is written as: f = V / λ[1]
- In this formula, f represents frequency, V represents the velocity of the wave, and λ represents the wavelength of the wave.
- Example: A certain sound wave traveling in the air has a wavelength of 322 nm when the velocity of sound is 320 m/s. What is the frequency of this sound wave?
-
2
Convert the wavelength into meters, if necessary. If the wavelength is given in nanometers, you need to convert this value into meters by dividing it by the number of nanometers in a single meter.[2]
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 322 nm
- 322 nm x (1 m / 10^9 nm) = 3.22 x 10^-7 m = 0.000000322 m
Advertisement
-
3
Divide the velocity by the wavelength. Divide the velocity of the wave, V, by the wavelength converted into meters, λ, in order to find the frequency, f.[3]
- Example: f = V / λ = 320 / 0.000000322 = 993788819.88 = 9.94 x 10^8
-
4
Write your answer. After completing the previous step, you will have completed your calculation for the frequency of the wave. Write your answer in Hertz, Hz, which is the unit for frequency.
- Example: The frequency of this wave is 9.94 x 10^8 Hz.
Advertisement
-
1
Learn the formula. The formula for the frequency of a wave in a vacuum is almost identical to that of a wave not in a vacuum. Since there are no outside influences on the velocity of the wave, though, you would use the mathematical constant for the speed of light, which electromagnetic waves would travel at under these conditions. As such, the formula is written as: f = C / λ[4]
- In this formula, f represents frequency, C represents the velocity or speed of light, and λ represents the wavelength of the wave.
- Example: A particular wave of electromagnetic radiation has a wavelength of 573 nm when passing through a vacuum. What is the frequency of this electromagnetic wave?
-
2
Convert the wavelength into meters, if necessary. When the problem gives you the wavelength in meters, no further action is needed. If, however, the wavelength is given in micrometers, you need to convert this value into meters by dividing it by the number of micrometers in a single meter.
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 573 nm
- 573 nm x (1 m / 10^9 nm) = 5.73 x 10^-7 m = 0.000000573
-
3
Divide the speed of light by the wavelength. The speed of light is a constant, so even if the problem does not provide you with a value, the value remains 3.00 x 10^8 m/s. Divide this value by the wavelength converted into meters.[5]
- Example: f = C / λ = 3.00 x 10^8 / 5.73 x 10^-7 = 5.24 x 10^14
-
4
Write your answer. With this, you should have calculated the value of the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 5.24 x 10^14 Hz.
Advertisement
-
1
Learn the formula. Frequency and the time taken to finish a single wave oscillation are inversely proportional. As such, the formula for calculating frequency when given the time taken to complete a wave cycle is written as: f = 1 / T
- In this formula, f represents frequency and T represents the time period or amount of time required to complete a single wave oscillation.
- Example A: The time for a certain wave to complete a single oscillation is 0.32 seconds. What is the frequency of this wave?
- Example B: In 0.57 seconds, a certain wave can complete 15 oscillations. What is the frequency of this wave?
-
2
Divide the number of oscillations by the time period. Usually, you will be told how long it takes to complete a single oscillation, in which case, you would just divide the number 1 by the time period, T. If given a time period for numerous oscillations, however, you will need to divide the number of oscillations by the overall time period required to complete them.[6]
- Example A: f = 1 / T = 1 / 0.32 = 3.125
- Example B: f = 1 / T = 15 / 0.57 = 26.316
-
3
Write your answer. This calculation should tell you the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example A: The frequency of this wave is 3.125 Hz.
- Example B: The frequency of this wave is 26.316 Hz.
Advertisement
-
1
Learn the formula. When told the angular frequency of a wave but not the standard frequency of that same wave, the formula to calculate the standard frequency is written as: f = ω / (2π)[7]
- In this formula, f represents the frequency of the wave and ω represents the angular frequency. As with any mathematical problem, π stands for pi, a mathematical constant.
- Example: A particular wave rotates with an angular frequency of 7.17 radians per second. What is the frequency of that wave?
-
2
Multiply pi by two. In order to find the denominator of the equation, you need to double the value of pi, 3.14.
- Example: 2 * π = 2 * 3.14 = 6.28
-
3
Divide the angular frequency by the double of pi. Divide the angular frequency of the wave, given in radians per second, by 6.28, the doubled value of pi.[8]
- Example: f = ω / (2π) = 7.17 / (2 * 3.14) = 7.17 / 6.28 = 1.14
-
4
Write your answer. This final bit of calculation should indicate what the frequency of the wave is. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 1.14 Hz.
Advertisement
Add New Question
-
Question
What is the frequency if 80 oscillations are completed in 1 second?
Frequency is the number of oscillations completed in a second. The answer would be 80 Hertz.
-
Question
Do atoms have a frequency and, if so, does it mean everything vibrates?
Atoms have energy. Energy is often characterized as vibration. Vibration possesses frequency. So, yes, everything could be thought of as vibrating at the atomic level.
-
Question
What’s the definition of frequency?
The rate at which a vibration occurs that constitutes a wave, either in a material (as in sound waves), or in an electromagnetic field (as in radio waves and light), usually measured per second. The rate at which something occurs or is repeated over a particular period of time or in a given sample.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To calculate the frequency of a wave, divide the velocity of the wave by the wavelength. Write your answer in Hertz, or Hz, which is the unit for frequency. If you need to calculate the frequency from the time it takes to complete a wave cycle, or T, the frequency will be the inverse of the time, or 1 divided by T. Display this answer in Hertz as well. Keep reading to learn how to calculate frequency from angular frequency!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,513,065 times.
Did this article help you?
Длина, скорость и частота электромагнитной волны.
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
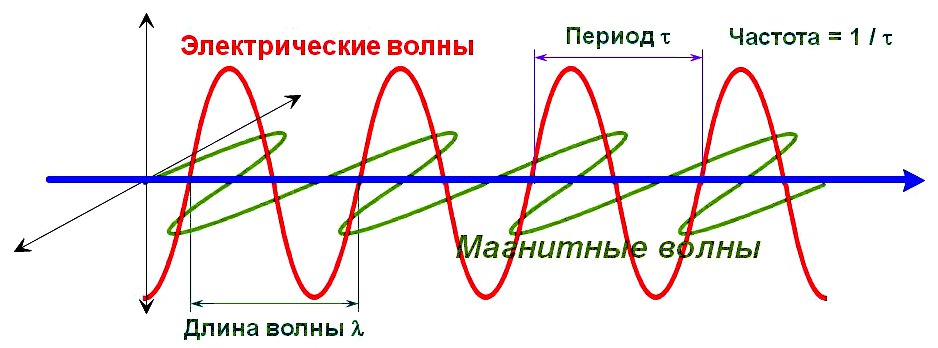
Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.
Рис.1
Длина волны, обозначаемая буквой λ и измеряемая в метрах —
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 — это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.
Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
|
Частота электромагнитных колебаний f |
||
Показатель преломления среды (по умолч. 1) |
||
Длина волны |
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
|
Длина электромагнитной волны в вакууме λ |
||
Частота |
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.
Как найти частоту волны? Процесс прост; количество оборотов, которое требуется для завершения конкретной вещи, называется частотой.
Когда объект движется, мы обычно определяем движение, силу и многие другие факторы. Но нам также нужно знать, с какой частотой он будет двигаться в данный момент времени. Таким образом, обратное время дается как частота в стандартных терминах.
В подробном случае мы также могли бы определить частоту данной волны, частицы в краткосрочной перспективе, а также более широкий контекст. частота является широко используемым фактором с точки зрения волны. Скажем, например, волна распространяется с определенной скоростью, и мы должны найти частоту волны.
Обычно мы погружаемся в математическую часть решения, но, говоря простым языком, мы также можем быстро определить волны. То частота сколько циклов он делает за одну секунду. Таким образом, если волна завершает один цикл, частота составляет половину от него.
Частота — это то, что появляется постоянно или в определенный момент времени. Подобно соленоиду, он имеет несколько витков при намотке на проводник и производит электричество. Точно так же частота — это количество циклов, которые волна совершает за одну секунду, и она обычно равна 2 герцам.
Компания количество циклов световой волны сделанное за одну секунду, также оценивается с точки зрения длины волны и скорость световой волны. Звуковая волна является наиболее распространенной областью, где часто рассматривается частотный термин.
Существует также научная вещь: собаки и птицы слышат звук за пределами определенного уровня, который даже люди не способны слышать. Мы созданы таким образом, что только определенное количество частота звука мы могли вынести услышать.
Частота волновой формулы
Частота имеет общую формулу, которую можно применять во всех контекстах. Период времени является основной причиной, которая помогает в формуле частоты.
Количество циклов, которые волна делает за один, рассматривается как частота этой конкретной волны. Следовательно, формула частоты в повседневном исчислении такова: f=1/T. Здесь Т — период времени, за который волны совершают число циклов.
Чтобы рассчитать частоту, нам нужно знать характеристики волны. Волна — это совокупность вибраций, называемых энергиями. Они достигли пика на обоих концах. Верхний узел называется впадина, а нижний узел называется гребень.
Высота волны обычно считается амплитудой волны. Высота волны будет определять, будет ли амплитуда больше или меньше. Поэтому, когда они изменяются, циклы, сделанные в секунду, также будут изменены.
Таким образом, когда волна завершает один цикл, то есть если волна имеет и гребень, и впадину в одной и той же фазе, тогда получаемая частота равна половине.
Волна совершает определенное количество циклов за одну секунду, что в основном известно как частота волны. И это дается формулой f=1/Т. Тип волны может зависеть от среды, через которую она проходит.
Как найти частоту волны по графику?
Теперь давайте посмотрим, как найти частоту волны на графике. Во-первых, частота — это количество циклов, которые волна пытается совершить, чтобы совершить один полный круг в данный конкретный момент времени.
Когда волна сделает один цикл, на это потребуется некоторое время. На графике мы называем это единицами. По сути, на графике есть несколько единиц, по которым мы можем быстро определить, как найти частоту волны в данном конкретном случае.
Скажем, например, волна движется с определенной скоростью, и мы также должны знать, сколько секунд это занимает. Скажи, что есть 12 секунд отмечены на графике, поэтому этой волне требуется 4 секунды, чтобы завершить один полный цикл. Итак, по формуле f=1/Т, частота волны 0.25Гц.
Давайте рассмотрим несколько задач по расчету частоты.
Проблема:
Типичная волна совершает два цикла за 30 секунд, и какова будет частота волны, если она будет распространяться в той же среде?
Решение:
f=1/Т
f=2/30
f=0.0667 Гц
Всегда возникает путаница между частота волны и скорость волны. Есть амплитуда волны, которая в основном является высотой волны. Таким образом, скорость рассчитывается, чтобы найти скалярную часть скорости, которая является скоростью.
Когда мы обнаруживаем, что волна является световой, звуковой или электромагнитной волной, нам нужно найти частоту волна, завершающая циклы. Период времени между циклами, совершаемыми волной, обычно определяется формулой как обратную частоту.
Как найти частоту волны по длине и амплитуде?
Как найти частоту волны по длине и амплитуде? Когда мы рассматриваем волну как свет, мы должны знать все факторы, влияющие на частоту волны.
Во-первых, необходимо учитывать длину волны. Как найти частоту волны с длиной волны? Формула очень проста, и нам нужно найти формулу скорости света.
Будет формула, называемая скоростью света, с = fλ. Здесь c — скорость света, f — определяемая частота, λ — длина волны света. Из этой формулы мы можем найти частоту волны через длину волны, переставив члены, данные в формуле.
Если говорят, что волна движется с определенной скоростью и временем, нам также нужно найти частота с которым распространяется световая волна. Таким образом, формула, упомянутая выше, будет использоваться для расчета частоты в заданный период времени.
Найдем частоту волны и посмотрим, как частота определяется по формуле.
Проблема:
Световая волна распространяется со скоростью 3×108 РС. Данную длину волны световой волны называют равной 2000 Å. Какова частота?
Решение:
с = fλ
f = с / λ
ф = 3×108 / 2000 Å
f= 1.5 х 1018 герц
Итак, из вышеприведенной задачи видно, что частоту можно найти, используя длину волны.
Теперь нам нужно знать, как найти частоту волны через амплитуду. Для этого рассмотрим теперь общую формулу частоты, т. е. f=1/Т. Здесь f также можно записать как f = ω / 2 π.
Здесь формула для T дается как 2 π/ω. Отсюда легко найти значение амплитуды, если упомянут период времени. А частоту можно найти по приведенной выше формуле, если в конкретной задаче задана амплитуда.
Как найти частоту волны, зная только длину волны?
Нам нужно знать, как длина волны влияет на волну, когда она распространяется с определенной скоростью и в заданном направлении. Это то, как далеко волна сможет пройти в среде.
Мы все знаем, что скорость света является стандартом для большинства формул, и мы также знаем, как переставить детали данной формулы, чтобы найти частоту данной волны. Как правило, когда световая волна распространяется в определенном направлении со скоростью 3×108, он также будет собирать информацию о частоте волны.
Формула скорости света является основой для определения длины волны или частоты распространяющейся световой волны. Скорость формулы света определяется выражением с = fλ. Отсюда мы получаем частоту волны через длину волны, соответствующим образом изменяя формулу.
Окончательная формула f = с / λ. Давайте посмотрим на проблему, как работает формула для электромагнитной волны.
Проблема:
Вычислите частоту электромагнитной волны, которая распространяется со скоростью 2×106м/с с длиной волны 1000 Å. С заданными деталями используйте формулу частота по длине волны.
Решение:
с = fλ
f = с / λ
f = 0.002 х 106 герц
f = 2 х 106/ 1000 Å
Таким образом, мы можем быстро определить частоту волны, используя значение скорости и, главным образом, значение длины волны.
Длина волны волны — это в основном пространство между гребнями или впадинами волны, которые следуют друг за другом. В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
Когда гребни и впадины волны, находящиеся в одной и той же фазе, встречаются в одном и том же месте, обычно считается, что это длина волны.
Как найти частоту волны по заданному периоду?
Как найти частоту волны через период времени? Ответ на этот вопрос прост, так как это общая формула для определения частоты волны.
Мы должны знать, что период времени в волне — это расстояние между гребнем и впадиной в одной и той же фазе. Поэтому, когда волна в основном распространяется с определенной частотой в заданный промежуток времени, нам нужна формула для расчета частоты.
Вот формула для частота с точки зрения периода времени, f=1/Т. Период времени обычно является еще одним термином для амплитуды волны. Т можно также записать как 2 π/ω, Где ω является мерой амплитуды.
Компания амплитуда — это в основном высота волны в зависимости от чего нам нужно сделать вывод, что амплитуда большая или малая. Если высота волны велика, то амплитуда называется значительной, а если высота волны мала, то говорят, что амплитуда волны мала.
Амплитуда имеет два конца, называемые гребень и впадина. Впадина — это верхний узел амплитуды, а гребень — нижний узел амплитуды.
Когда расстояние между двумя волнами называется длиной волны, а количество циклов, которое совершает одна волна, называется частота, когда период времени равен единице единица на графике, что в стандартном выражении составляет одну секунду.
Как найти частоту волны без скорости?
Из формулы скорости света мы могли бы заметить, что длина волны обратно пропорциональна частоте волны, то есть циклам, совершаемым волной за период времени.
Мы также знаем, что частота не прямо пропорциональна периоду времени; следовательно, длина волны и период времени пропорциональны друг другу. Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Мы предполагаем, что длина волны и период времени пропорциональны, а частота и энергия быть пропорциональным. Частота волны без скорости была бы формулой энергии, где E=hf, где E — энергия, h — постоянная Планка, f — частота.
Итак, зная конкретную базовую формулу света и энергии, мы можем соответствующим образом переставить термины и узнать, как найти частоту волны во всех возможных терминах. Кроме того, все эти факторы влияют на волну и ее количество, способствуя ее собственному распространению.
Как вычислить частоту
Частота – физическая величина, отражающая число колебаний в механическом, электромагнитном или ином процессе. Помимо обычной линейной частоты, рассматривают циклическую (угловую) частоту при вращении тел. Нахождение данных величин в различных задачах осуществляется с использованием известных формул, соотношений параметров тел и показателей их движения.

Инструкция
В начале решения любой задачи приведите все известные величины к единицам, принятым в системе СИ. Линейная частота измеряется в герцах (Гц), циклическая – в радианах за одну секунду.
При решении задачи на распространение волн с известной длиной и скоростью колебаний вычислите их частоту по формуле: F=v/λ, где λ — длина волны (м), v — скорость распространения колебаний в среде (м/с). Если в задаче задан лишь период T (с) совершаемых телом колебаний, частота находится из соотношения: F=1/T (Гц).
Чтобы узнать линейную частоту колебаний F через заданную циклическую в момент вращения тела, используйте следующее выражение: F=ω/(2*π), где ω — циклическая частота (рад/с), π – константа, примерно равная 3,14. Отсюда можно вывести и обратную формулу нахождения циклической частоты по заданному значению линейной: ω=2*π*F.
Допустим задана колебательная система, состоящая из подвешенного груза известной массы M (м) и пружины с определенной жесткостью k (Н/м). Вычислите частоту колебаний груза F, проведя следующие действия. Найдите период колебаний по формуле T=2*π √(M/k), подставьте известные значения и высчитайте период в секундах. По выше приведенной формуле определите частоту колебаний подвешенного тела: F=1/T (Гц).
При решении задач из раздела электродинамики рассматривается электромагнитный колебательный контур. Пусть он состоит из пары параллельно соединенных конденсаторов емкостью С (Ф) и катушки индуктивности L (Гн). Вычислить частоту собственных колебаний можно по формуле: ω = 1/√(L*C) (рад/c).
Если значение силы тока I (А) задано следующим уравнением i = 0,28*sin70*π*t (t — выражено в секундах) и при этом требуется вычислить циклическую ω и линейную частоту F колебаний, выполните следующие действия. В общем виде уравнение синусоидального тока выглядит так: i = Im*sin(ωt+φ0). Следовательно в данном случае известно, что амплитуда колебаний Im = 0,28 А, начальная фаза φ0 равна нулю, угловая (циклическая) частота ω = 70*π рад/c, так как она является в заданном уравнении коэффициентом при t. Отсюда вычислите линейную частоту F = ω/(2*π) = 70*π/(2*π) = 35 Гц.
Видео по теме
Источники:
- линейная частота
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.