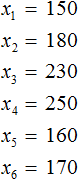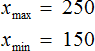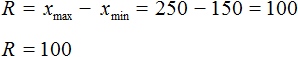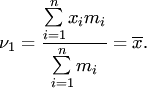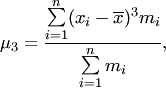Как найти частоты в математической статистике - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.

1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.^[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
3

Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:^[2]

Реклама

1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.^[3]
- В нашем примере набор данных содержит 16 чисел.
2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.^[4]
- Например, в нашем примере число встречается в наборе данных три раза.
3

Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.^[5]

Реклама

1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.^[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама

Советы

Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.

Источники

Об этой статье

Эту страницу просматривали 145 557 раз.

Была ли эта статья полезной?

Источник

Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.

Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).

Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.

На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.

Выборка. Объем. Размах

Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней

Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6

n = 6

Элементы выборки обозначаются с помощью переменных с индексами . Последний элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.

Обозначим элементы нашей выборки через переменные

Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.

Размахом выборки называют разницу между самым большим и маленьким элементом выборки.

В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100

Среднее арифметическое

Понятие среднего значения часто используется в повседневной жизни.

Примеры:

средняя зарплата жителей страны;
средний балл учащихся;
средняя скорость движения;
средняя производительность труда.

Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.

Среднее арифметическое — это результат деления суммы элементов выборки на их количество.

Вернемся к нашему примеру

Узнаем сколько в среднем мы тратили в каждом из шести дней:

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

66,2 × 3 = 198,6 км.

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

78,4 × 2 = 156,8 км.

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

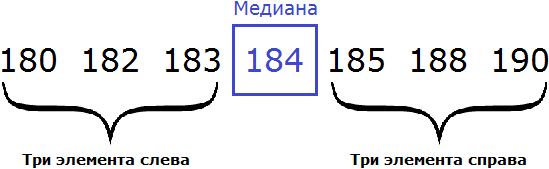
Выпишем рост спортсменов отдельно:

180, 182, 183, 184, 185, 188, 190

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.

Частота

Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.

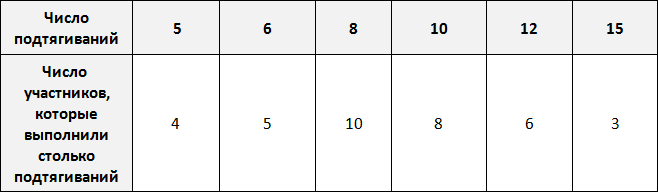
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.

Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.

Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.

Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:

4 + 5 + 10 + 8 + 6 + 3 = 36

Относительная частота

Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.

Относительная частота равна отношению частоты на общее число элементов выборки.

Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Элементы
математической статистики. Выборочный
метод

Генеральная
и выборочная совокупности. Статистические
распределения выборок. Кумулята и ее
свойства. Гистограмма и полигон
статистических распределений. Числовые
характеристики: выборочная средняя;
дисперсия выборки; среднеквадратическое
отклонение; мода и медиана для дискретных
и интервальных статистических
распределений выборки; эмпирические
начальные и центральные моменты,
асимметрия и эксцесс.

Установление
закономерностей, которым подчинены
массовые случайные явления, основано
на изучении статистических данных —
результатах наблюдений. Первая задача
математической статистики — указать
способы сбора и группировки (если данных
очень много) статистических сведений.
Вторая задача математической статистики
— разработать методы анализа статистических
данных в зависимости от цели исследования.
Изучение тех или иных явлений методами
математической статистики служит
средством решения многих вопросов,
выдвигаемых наукой и практикой (правильная
организация технологического процесса,
наиболее целесообразное планирование
и др.).

Итак,
задача математической статистики
состоит в создании методов сбора и
обработки статистических данных для
получения научных и практических
выводов.

Генеральная
и выборочная совокупности

Пусть
требуется изучить совокупность однородных
объектов относительно некоторого
качественного или количественного
признака, характеризующего эти объекты.
Например, для партии деталей качественным
признаком может служить стандартность
детали, а количественным — контролируемый
размер детали. Иногда проводят сплошное
обследование, т. е. обследуют каждый из
объектов совокупности относительно
признака, которым интересуются. На
практике, однако, сплошное обследование
применяется сравнительно редко. Например,
если совокупность содержит большое
число объектов, то провести сплошное
обследование физически невозможно.
Если обследование объекта связано с
его уничтожением или требует больших
материальных затрат, то случайным
образом отбирают из всей совокупности
ограниченное число объектов и подвергают
их изучению.

Выборочной
совокупностью,
или просто выборкой,
называют совокупность случайно отобранных
объектов.

Генеральной
совокупностью называют
совокупность объектов, из которых
проводится выборка.

Объемом совокупности
(выборочной или генеральной) называют
число объектов этой совокупности.

Часто
генеральная совокупность содержит
конечное число объектов. Однако если
это число достаточно велико, то иногда
для упрощения вычислений или для
облегчения теоретических выводов,
допускают, что генеральная совокупность
состоит из бесчисленного множества
объектов. Такое допущение оправдывается
тем, что увеличение объема генеральной
совокупности (достаточно большого
объема) практически не сказывается на
результатах обработки данных выборки.

Статистические
распределения выборок

В
результате статистической обработки
материалов можно подсчитать число
единиц, обладающих конкретным значением
того или иного признака. Каждое отдельное
значение признака будем обозначать и
называть вариантой,
а абсолютное число, показывающее, сколько
раз встречается та или иная варианта,
— частотой и
обозначать .

Если
отдельные значения признака (варианты)
расположим в возрастающем или убывающем
порядке и относительно каждой варианты
укажем, как часто она встречается в
данной совокупности, то получим статистическое
распределение признака,
или вариационный
ряд.
Он характеризует изменение (варьирование)
какого-нибудь количественного признака.
Следовательно, вариационный ряд
представляет собой две строки (или
колонки). В одной из них приводятся
варианты, в другой — частоты.

Вариация
признака может быть дискретной и
непрерывной. Дискретной называетсявариация,
при которой отдельные значения признака
(варианты) отличаются друг от друга на
некоторую конечную величину (обычно
целое число); Например: количество детей
в семье; оценки, полученные студентами
на экзамене; размеры обуви, проданной
за день фирмой.

Непрерывной называется вариация,
при которой значения признака могут
отличаться одно от другого на сколь
угодно малую величину. Например: стоимость
реализованной продукции; уровень
рентабельности предприятия; процент
занятости трудоспособного населения;
депозитная ставка коммерческих банков.

При
непрерывной вариации распределение
признака называется интервальным.
Частоты относятся не к отдельному
значению признака, а ко всему интервалу.
Часто значением интервала принимают
его середину, т. е. центральное значение.

Нередко
вместо абсолютных значений частот
используют относительные. Для этого
можно использовать долю частоты того
или иного варианта (а также интервала)
в сумме всех частот. Такая величина
называется относительной
частотой и
обозначается .
Для получения относительных частот
необходимо соответствующую частоту
разделить на сумму всех частот:
где —
относительная частота варианты или
интервала соответственно первой, второй
и т. д.

Сумма
всех относительных частот равна единице:

Относительные
частоты можно выражать и в процентах
(тогда их сумма равна 100%).

В
интервальном вариационном ряду в каждом
интервале различают нижнюю и верхнюю
границы интервала:
нижняя граница интервала ;
верхняя граница интервала величина
интервала .
Как правило, при построении интерваль-ных
вариационных рядов в каждый интервал
включаются варианты, числовые значения
которых больше нижней границы и меньше
или равны верхней границе. Интервальные
вариационные ряды бывают с одинаковыми
и неодинаковыми интервалами. В последнем
случае чаще всего встречаютсяпоследовательно
увеличивающиеся интервалы.
Для выбора оптимальной
величины интервала,
т. е. такой, при которой вариационный
ряд не будет громоздким и будут сохранены
особенности явления, можно рекомендовать
формулу

где —
число единиц в совокупности.

Так,
если в совокупности 200 единиц, наибольший
вариант равен 49,961, а наименьший — 49,918,
то

Следовательно,
в данном случае оптимальной величиной
интервала может служить 0,005.

Гистограмма
и полигон статистических распределений.
Кумулята

Для
наглядного представления вариационного
ряда большое значение имеют его
графические изображения. Графически
вариационный ряд может быть изображен
в виде полигона, гистограммы и кумуляты.

Полигон
распределения (дословно
— многоугольник распределения) строится
в прямоугольной системе координат.
Величина признака откладывается на оси
абсцисс, частоты или относительные
частоты — по оси ординат. Чаще всего
полигоны применяются для изображения
дискретных вариационных рядов, но их
можно применять также для интервальных
рядов. В этом случае на оси абсцисс
откладываются точки, соответствующие
серединам данных интервалов.

Гистограмма
распределения строится
аналогично полигону в прямоугольной
системе координат. В отличие от полигона
при построении гистограммы на оси
абсцисс выбирают не точки, а отрезки,
изображающие интервал, а вместо ординат,
соответствующих частотам или относительным
частотам отдельных вариант, строят
прямоугольники с высотой, пропорциональной
частотам или относительным частотам
интервала. В случае интервалов различной
длины гистограмма распределения
строится, не по частотам или относительным
частотам, а по плотности интервалов
(абсолютной или относительной). При этом
общая площадь гистограммы равна
численности совокупности, если построение
проводится по абсолютной плотности,
или единице, если гистограмма построена
по относительной плотности.

Если
соединить прямыми линиями середины
верхних сторон прямоугольников, то
получим полигоны распределения.

Разбивая
интервалы на несколько частей и исходя
из того, что вся — площадь гистограммы
должна остаться при этом неизменной,
можно получить мелкоступенчатую
гистограмму, которая при уменьшении
величины интервала будет приближаться
к плавной кривой, называемой кривой
распределения.

Кумулятивная
кривая (кривая
сумм — кумулята) получается при
изображении вариационного ряда с
накопленными частотами или относительными
частотами в прямоугольной системе
координат, Накопленная частота
определенной варианты получается
суммированием всех частот вариант,
предшествующих данной, с частотой этой
варианты. При построении кумуляты
дискретного признака по оси абсцисс
откладывают значения признака (варианты),
Ординатами служат вертикальные отрезки,
длина которых пропорциональна накопленной
частоте или относительной частоте той
или иной варианты. Соединением вершин
ординат прямыми линиями получаем ломаную
(кривую) кумуляту.

При
построении кумуляты интервального
вариационного ряда нижней границе
первого интервала соответствует частота,
равная нулю, а верхней — вся частота
интервала. Верхней границе второго
интервала соответствует накопленная
частота первых двух интервалов (т. е.
сумма частот этих интервалов) и т. д.
Верхней границе последнего (максимального)
интервала соответствует накопленная
частота, равная сумме всех частот.

Числовые
характеристики выборки

В
качестве одной из важнейших характеристик
вариационного ряда применяют среднюю
величину. Математическая статистика
различает несколько типов средних
величин: арифметическую, геометрическую,
гармоническую, квадратическую, кубическую
и др. Все перечисленные типы средних
могут быть рассчитаны для случаев, когда
каждая из вариант вариационного ряда
встречается только один раз (тогда
средняя называется простой, или
невзвешенной) и когда варианты или
интервалы повторяются. При этом число
повторений вариант или интервалов
называют частотой,
или статистическим
весом,
а среднюю, вычисленную с учетом
статистического веса, — взвешенной
средней.

Для
характеристики вариационного ряда один
из перечисленных типов средних выбирается
не произвольно, а в зависимости от
особенностей изучаемого явления и цели,
для которой среднее исчисляется.

Практически
при выборе того или иного типа средней
следует исходить из принципа осмысленности
результата при суммировании или при
взвешивании. Только тогда средняя
применена правильно, когда в результате
взвешивания или суммирования получаются
величины, имеющие реальный смысл.

Обычно
затруднения при выборе типа средней
возникают лишь в использовании средней
арифметической, или гармонической. Что
же касается геометрической и квадратической
средних, то их применение обусловлено
особыми случаями (см. далее).

Следует
иметь в виду, что средняя только в том
случае является обобщающей характеристикой,
если она применяется к однородной
совокупности. В’ случае использования
средней для неоднородных совокупностей
можно прийти к неверным выводам. Научной
основой статистического анализа является
метод статистических группировок, т.
е. расчленения совокупности на качественно
однородные группы.

Все
указанные типы средних величин можно
получить из формул степенной средней.
Если имеются варианты ,
то среднюю из вариант можно рассчитать
по формуле простой невзвешенной степенной
средней порядка :

При
наличии соответствующих частот средняя
рассчитывается по формуле взвешенной
степенной средней:

Здесь  —
степенная средняя;  —
показатель степени, определяющий тип
средней;  —
варианты,  —
частоты или статистические веса
вариантов.

Средняя
арифметическая получается
из формулы степенной средней при
подстановке :

незвешенная ;
взвешенная

Средняя
гармоническая получается
при подстановке в формулу степенной
средней значения :

незвешенная ;
взвешенная

Средняя
гармоническая вычисляется тогда, когда
средняя предназначается для расчета
сумм слагаемых, обратно пропорциональных
величине данного признака, т. е. когда
суммированию подлежат не сами варианты,
а обратные им величины .

Средняя
квадратическая получается
из формулы степенной средней при
подстановке :

незвешенная ;
взвешенная

Средняя
квадратическая используется только
тогда, когда варианты представляют
собой отклонения фактических величин
от их средней арифметической или от
заданной нормы.

Средняя
геометрическая получается
из формулы степенной средней при
предельном переходе :

незвешенная ;
взвешенная

Вычисления
средней геометрической в значительной
мере упрощаются применением
логарифмирования:

незвешенная ;
взвешенная

Таким
образом, логарифм средней геометрической
есть средняя арифметическая из логарифмов
вариантов. Средняя геометрическая
используется главным образом при
изучении динамики. Средние коэффициенты
и темпы роста рассчитывают по формулам
средней геометрической.

Если
вычислить различные типы средних для
одного и того же вариационного ряда, то
числовые их значения будут различаться.
При этом средние по своей величине
расположатся в определенном порядке.
Наименьшей из перечисленных средних
окажется средняя гармоническая, затем
геометрическая и т. д., наибольшей будет
средняя квадратическая. При этом порядок
возрастания средних определяется
показателем степени z в формуле степенной
средней. Так, при  получаем
среднюю гармоническую, при  —
геометрическую, при  —
арифметическую, при  —
квадратическую:

В
качестве характеристики вариационного
ряда используют медиану ,
т. е. такое значение варьирующего
признака, которое приходится на середину
упорядоченного вариационного ряда.
Если в вариационном ряду  случаев,
то значение признака у случая  будет
медианным. Если в ряду четное
число  случаев,
то медиана равна средней арифметической
из двух срединных значений. При нечетном
количестве вариантов медиана рассчитывается
по формуле

;
при чётном

При
расчете медианы интервального
вариационного ряда сначала находят
интервал, содержащий медиану, путем
использования накопленных или
относительных частот. Медианному
интервалу соответствует первая из
накопленных или относительных частот,
превышающая половину всего объема
совокупности. Для нахождения медианы
при постоянстве плотности внутри
интервала, содержащего медиану, используют
формулу

где  —
нижняя граница медианного интервала;  —
величина медианного интервала;  —
накопленная частота интервала,
предшествующего медианному;  –частота
медианного интервала.

Медиану
можно определить также графически по
кумуляте. Для этого последнюю ординату,
пропорциональную сумме всех частот или
относительных частот, делят пополам.
Из полученной точки восстанавливают
перпендикуляр до пересечения с кумулятой.
Абсцисса точки пересечения — значение
медианы (см. рис. 29).
Медиана обладает
таким свойством: сумма абсолютных
величин отклонений вариантов от медианы
меньше, чем от любой другой величины (в
том числе и от средней арифметической):

Это
свойство медианы можно использовать
при проектировании расположения
трамвайных и троллейбусных остановок,
бензоколонок и т. д.

Модой называется
варианта, наиболее часто встречающаяся
в данном вариационном ряду. Для дискретного
ряда мода, являющаяся характеристикой
вариационного ряда, определяется по
частотам вариант и соответствует
варианте с наибольшей частотой. В случае
интервального распределения с равными
интервалами модальный интервал (т. е.
содержащий моду) определяется по
наибольшей частоте, а при неравных
интервалах — по наибольшей плотности.
Мода рассчитывается по формуле

где  —
нижняя граница модального интервала;  —
величина модального интервала;  —
частота модального интервала;  частота
интервала, предшествующего модальному;  —
частота интервала, следующего за
модальным

Вариационные
ряды, в которых частоты вариант,
равноотстоящих от средней, равны между
собой, называются симметричными.
Особенность симметричных вариационных
рядов состоит в равенстве трех
характеристик — средней арифметической,
моды и медианы:

(это
необходимое условие симметричности
вариационного ряда, но не достаточное)

Вариационные
ряды, в которых расположение вариант
вокруг средней не одинаково, т. е. частоты
по обе стороны от средней изменяются
по-разному, называются асимметричными,
илискошенными.
Различают асимметрию — левостороннюю
и правостороннюю

Средние
величины, характеризуя вариационный
ряд одним числом, не учитывают вариацию
признака, между тем эта вариация
существует. Для измерения вариации
признака в математической статистике
применяют ряд способов.

Вариационный
размах ,
или широта
распределения,
есть разность между наибольшим и
наименьшим значениями вариационного
ряда:

Вариационный
размах представляет собой величину
неустойчивую, чрезвычайно зависящую
от случайных обстоятельств; применяется
для приблизительной оценки вариации.

Среднее
линейное отклонение,
или простое
среднее отклонение (обозначается )
представляет собой среднюю арифметическую
из абсолютных значений отклонений
вариант от средней. В зависимости от
отсутствия или наличия частот вычисляют
среднее линейное отклонение невзвешенное
или взвешенное:

Средний
квадрат отклонения,
или дисперсия (обозначается )
наиболее часто применяется как мера
колеблемости признака. Дисперсии
невзвешенную и взвешенную вычисляют
по формулам

Таким
образом, дисперсия есть средняя
арифметическая из квадратов отклонений
вариант от их средней арифметической.
Квадратный
корень из дисперсии называется среднеквадратическим
отклонением.

Обобщающими
характеристиками вариационных рядов
являются моменты
распределения.
Характер распределения можно определить
с помощью небольшого количества моментов.

Средняя
из k-х степеней отклонений вариант от
некоторой постоянной величины называется моментом
k-го порядка:

При
расчете средних в качестве весов можно
использовать частоты, относительные
частоты или вероятности. При использовании
в качестве весов частот или относительных
частот моменты называются эмпирическими,
а при использовании вероятностей
— теоретическими.
Порядок момента определяется величиной .
Эмпирический момент k-го порядка находится
как отношение суммы произведений k-х
степеней отклонений вариант от постоянной
величины на
частоты к сумме частот:

В
зависимости от выбора постоянной
величины различают
следующие моменты.

1.
Если ,
то моменты называются начальными,
обозначаются и
вычисляются по формуле

Тогда
при получаем
начальный момент нулевого порядка:

при получаем
начальный момент первого порядка:

при получаем
начальный момент второго порядка:

при получаем
начальный момент третьего порядка:

при получаем
начальный момент четвёртого порядка:

и
т. д. Практически используют моменты
первых четырёх порядков.

2.
Если  не
равно нулю, а некоторой произвольной
величине  (начало
отчёта), то моменты называются начальными
относительно ,
обозначаются  и
рассчитываются по формуле

3.
Если за постоянную величину взять
среднюю ,
то моменты называютсяцентральными,
обозначаются и
вычисляются так

Тогда
при

то
есть центральный момент нулевого
порядка, равный единице;

при
k=1

то
есть центральный момент первого порядка
равен нулю;

при
k=2

то
есть центральный момент первого порядка
равен дисперсии и служит мерой колеблемости
признака;

при
k=3

в
этом случае центральный момент третьего
порядка служит мерой асимметрии
распределения признака. Если распределение
симметрично, то ;

при
k=4

получаем
центральный момент четвёртого порядка.

Коэффициентом
асимметрии называется
отношение центрального момента третьего
порядка к кубу среднеквадратического
отклонения:

Если
полигон вариационного ряда скошен, то
есть одна из его ветвей начиная от
вершины зримо короче другой, то такой
ряд называется асимметричным.

Эксцессом называется
уменьшенное на три единицы отношение
центрального момента четвёртого порядка
к четвёртой степени среднеквадратического
отклонения:

Кривые
распределения, у которых ,
менее крутые, имеют более плоскую вершину
и называются плосковершинными.
Кривые распределения, у которых ,
более крутые, имеют острую вершину и
называются островершинными.

Источник

Download Article

Preparing, calculating, and reporting your data

Download Article

Absolute frequency is a simple concept to grasp: it refers to the number of times a particular value appears in a specific data set (a collection of objects or values). However, relative frequency can be a little trickier. It refers to the proportion of times a particular value appears in a specific data set. In other words, relative frequency is, in essence, how many times a given event occurs divided by the total number of outcomes. If you organize your data, calculating and presenting relative frequency can become a simple task.

1
Collect your data. Unless you are just completing a math homework assignment, calculating relative frequency generally implies that you have some form of data. Conduct your experiment or study and collect the data. Decide how precisely you wish to report your results.^[1]
- For example, suppose you are collecting data on the ages of people who attend a particular movie. You could decide to collect and report the exact age of everyone who attends. But this is likely to give you 60 or 70 different results, being every number from about 10 through 70 or 80. You may instead wish to collect data in groups, like “Under 20,” “20-29,” “30-39,” “40-49,” “50-59,” and “60 plus.” This would be a more manageable set of six data groups.
- As another example, a doctor might collect body temperatures of patients on a given day. In this case, just collecting whole numbers, like 97, 98, 99, might not be precise enough. It might be necessary to report data in decimals in this case.
2
Sort the data. After you complete your study or experiment, you are likely to have a collection of data values that could look like 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. In this form, the data appear almost meaningless and difficult to use. It is more helpful to sort the data in order from lowest to highest. This would result in the list 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.
- When you are sorting and rewriting your collection of data, be careful to include every point correctly. Count the data set to make sure you do not leave off any values.
Advertisement
3
Use a data table. You can summarize the results of your data collection by creating a simple data frequency table. This is a chart with three columns that you will use for your relative frequency calculations. Label the columns as follows:^[2]
- . This column will be filled with each value that appears in your data set. Do not repeat items. For example, if the value 4 appears several times in the list, just put under the column once.
- , or . In statistics, the variable is conventionally used to represent the count of a particular value. You may also write , which is read as “n of x,” and means the count of each x-value. A final alternative is , which means the “frequency of x.” In this column, you will put the number of times that the value appears. For example, if the number 4 appears three times, you will place a 3 next to the number 4.
- Relative Frequency or . This final column is where you will record the relative frequency of each data item or grouping. The label , which is read “P of x,” could mean the probability of x or the percentage of x. The calculation of relative frequency appears below. This column will be used after you complete that calculation for each value of x.

1
Count your full data set. Relative frequency is a measure of the number of times a particular value results, as a fraction of the full set. In order to calculate relative frequency, you need to know how many data points you have in your full data set. The will become the denominator in the fraction that you use for calculating.^[3]
- In the sample data set provided above, counting each item results in 16 total data points.
2
Count each result. You need to determine the number of times that each data point appears in your results. You may want to calculate the relative frequency of one particular item, or you may be summarizing the overall data for the full data set.^[4]
- For example, in the data set provided above, consider the value . This value appears three times in the list.
3

Divide each result by the total size of the set. This is the final calculation to determine the relative frequency of each item. You can set it up as a fraction or use a calculator or spreadsheet to perform the division.^[5]

1
Present your results in a frequency table. The frequency table that you began above can be used to present the results in a format that is easy to review. As you perform each of the calculations, fill in the results in the corresponding places in the table. It is common to round your answers to two decimal places, although you will need to decide this for yourself based on the needs of your study. Because of rounding the end result may total something close to , but not exactly 1.0.^[6]
- For example, using the data set above, the relative frequency table would appear as follows:
- x : n(x) : P(x)
- 1 : 3 : 0.19
- 2 : 1 : 0.06
- 3 : 2 : 0.13
- 4 : 3 : 0.19
- 5 : 4 : 0.25
- 6 : 2 : 0.13
- 7 : 1 : 0.06
- total : 16 : 1.01
2
Report items that do not appear. It may be just as meaningful to report items whose frequency is 0 as to report those items that do appear in your data set. Look at the kind of data you are collecting, and if you notice any gaps in your sorted data, you may need to report them as 0s.
- For example, the sample data set you have been working with includes all values from 1 to 7. But suppose that the number 3 never appeared. That could be important, and you would report the relative frequency of the value 3 as 0.
3
Show your results as percentages. You may wish to turn your decimal results into percentages. This is a common practice, as relative frequency is often used as a predictor of the percentage of times that some value will occur. To convert a decimal number to a percentage, simply shift the decimal point two spaces to the right, and add a percent symbol.^[7]
- For example, the decimal result of 0.13 is equal to 13%.
- The decimal result of 0.06 is equal to 6%. (Don’t just skip over the 0.)

Add New Question

Question

What is frequency of the event?

It’s a measurement of how often the event occurs in a given time period.
Question

How can you calculate frequency from relative frequency?

The word «frequency» alone is not very clear. In statistics, there are absolute frequency (the number of times a data point appears), relative frequency (usually presented as a percentage), or cumulative frequency. Cumulative frequency begins at 0 and adds up the frequencies as you move through your list. If you are just asked for «frequency,» from the relative frequency, it probably means the absolute frequency. Take your relative frequency, and multiply it by the total number of items in the full data set, and you will have the absolute frequency.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Physically speaking, the relative frequency tells you the presence or occurrence of a particular event in a set of events.
If you add up the relative frequencies of all items in a data set, you should get a sum of 1. If you round off your values, the sum may not be exactly 1.0.
If your data set is too large for simple counting, you may need to use a software package like MS-Excel or MATLAB to avoid mistakes.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To stop face sweating, try applying an astringent containing tannic acid, like witch hazel, to your face twice a day using a cotton ball. Additionally, apply an antiperspirant spray to your scalp, temples, and upper forehead to temporarily block your sweat glands. Alternatively, try using a dry shampoo to manage scalp sweating by holding it 8 inches from your head, then spraying it in 2 inch sections of your hair at a time. After that, massage the dry shampoo into your scalp for even distribution. For more tips, like how to show your results as percentages, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 103,319 times.

Did this article help you?

Источник

Построение полигона, гистограммы, кумуляты, огивы

Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.

Полигон
Гистограмма
Кумулята и огива

Полигон

Полигоном частот называют
ломаную, отрезки которой соединяют точки

. Для построения полигона частот на оси
абсцисс откладывают варианты

, а на оси ординат – соответствующие им
частоты

. Такие точки

соединяют
отрезками прямых и получают полигон частот.

Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки

. Для построения полигона относительных
частот на оси абсцисс откладывают варианты

, а на оси ординат – соответствующие им
относительные частоты (частости)

. Такие точки

соединяют
отрезками прямых и получают полигон частот.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Пример 1

Построить полигон частот и
полигон относительных частот (частостей):

Решение

Вычислим относительные
частоты (частости):

Полигон частот

Полигон относительных частот

В случае интервального ряда для
построения полигона в качестве

берутся середины интервалов.

Гистограмма

В случае интервального
статистического распределения целесообразно построить гистограмму.

Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною

, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты

. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.

В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте

, а в случае неравных интервалов высота
равна плотности относительной частоты

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Пример 2

Построить гистограмму
частот и относительных частот (частостей)

Гистограмма частот

Гистограмма относительных частот

Пример 3

Построить гистограмму
частот (случай неравных интервалов).

Решение

Вычислим плотности
частоты:

Гистограмма частот

Кроме этой задачи на другой странице сайта есть

пример построения полигона и гистограммы на одном графике для интервального вариационного ряда

Кумулята и огива

При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.

Пример 4

Построить кумулятивную
кривую:

Решение

Вычислим накопленные
частоты:

Кумулятивная кривая

Источник