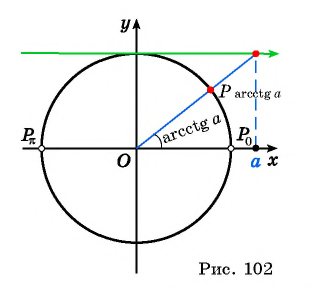
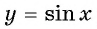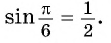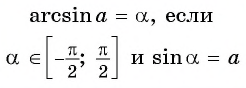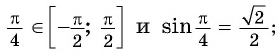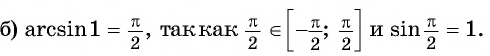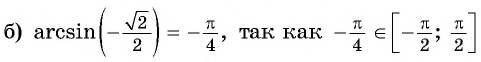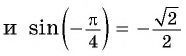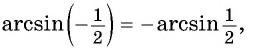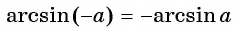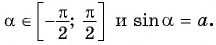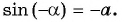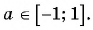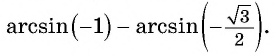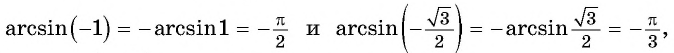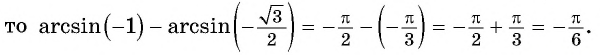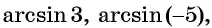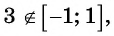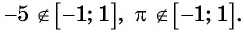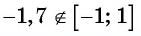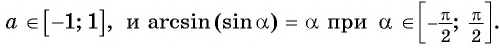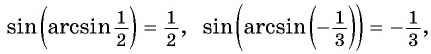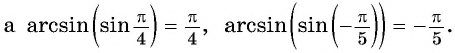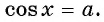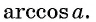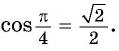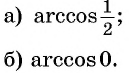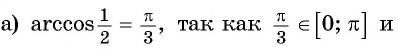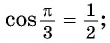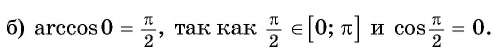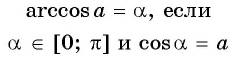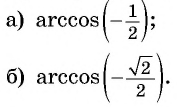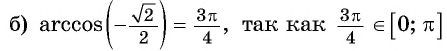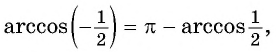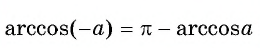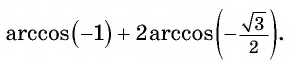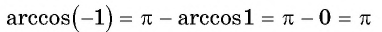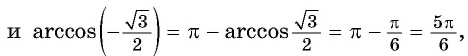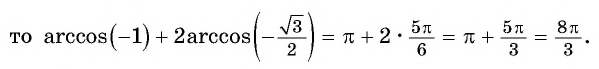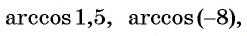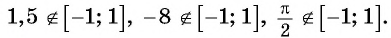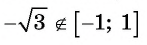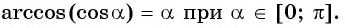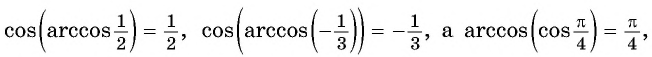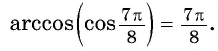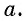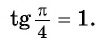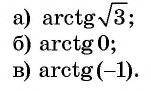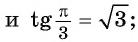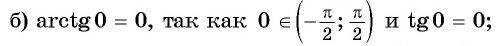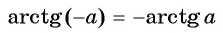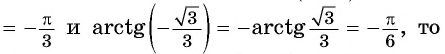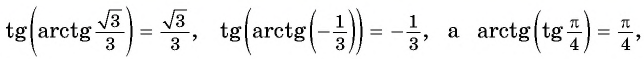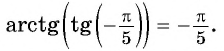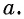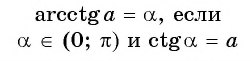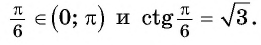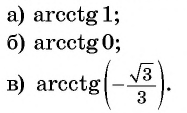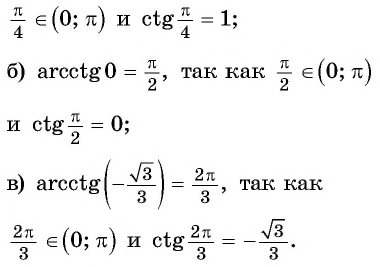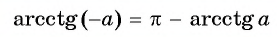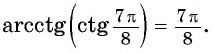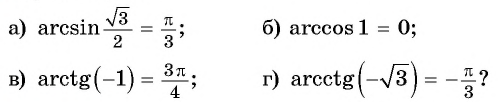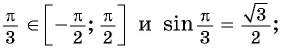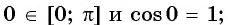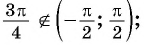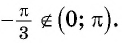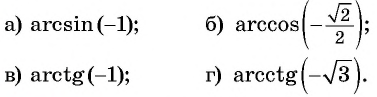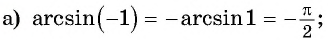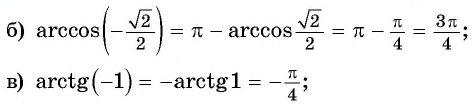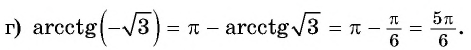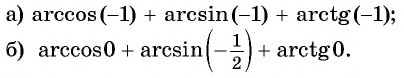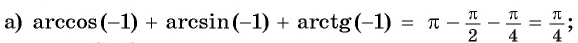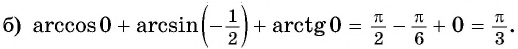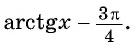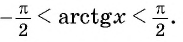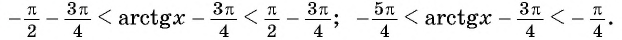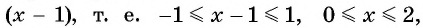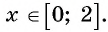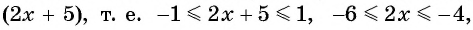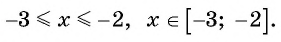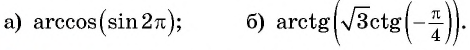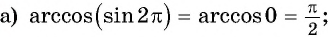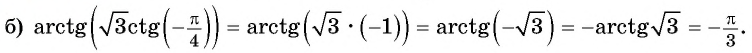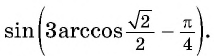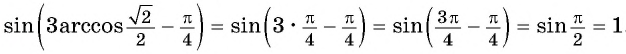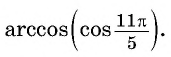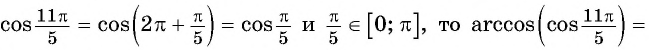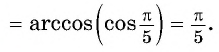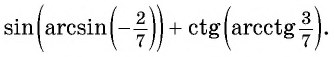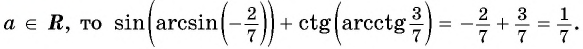- Определение
- График арккосинуса
- Свойства арккосинуса
- Таблица арккосинусов
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
Свойства арккосинуса
Ниже в табличном виде представлены основные свойства арккосинуса с формулами.
Таблица арккосинусов
| x | arccos x (рад) | arccos x (°) |
| -1 | π | 180° |
| -√3/2 | 5π/6 | 150° |
| -√2/2 | 3π/4 | 135° |
| -1/2 | 2π/3 | 120° |
| 0 | π/2 | 90° |
| 1/2 | π/3 | 60° |
| √2/2 | π/4 | 45° |
| √3/2 | π/6 | 30° |
| 1 | 0 | 0° |
microexcel.ru
Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Нахождение значения аргумента
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки 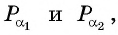
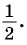
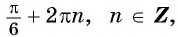
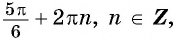
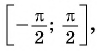
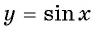
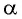
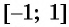
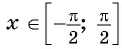
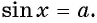
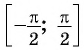
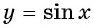
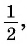
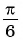
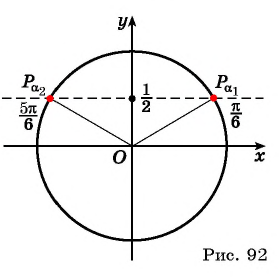
Определение Арксинуса
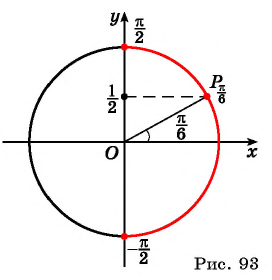
Определение:
Арксинусом числа 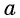
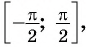
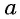
Этот угол обозначают 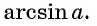
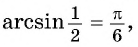
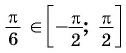
Пример №1
Вычислите:
Решение:
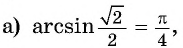
Пример №2
Найдите значение выражения:
Решение:
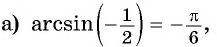
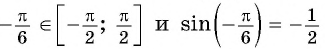
Заметим, что 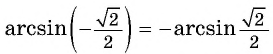
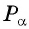
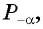
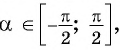
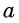
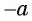
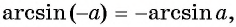
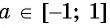
Пусть 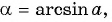
Так как точки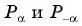
Поскольку 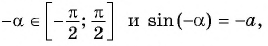
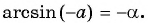
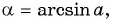
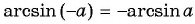
Воспользуемся полученным равенством и найдем значение выражения
Так как
Отметим, что областью определения выражения 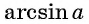
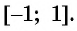
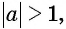
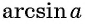
Например, выражения 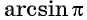
Выражение 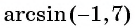
Из определения арксинуса числа следует, что 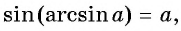
Например,
Рассмотрим промежуток 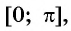
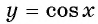
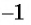
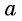
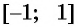
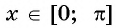
Определение Арккосинуса
Определение:
Арккосинусом числа 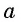
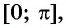
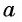
Этот угол обозначают
Например: 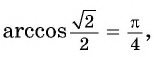
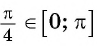
Пример №3
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
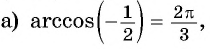
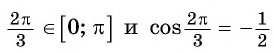
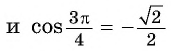
Заметим, что 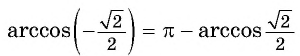
Пусть 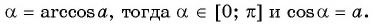
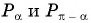
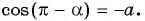
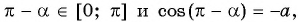
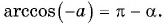
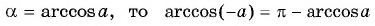
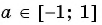
Воспользуемся полученным равенством и найдем значение выражения
Так как
Областью определения выражения 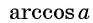
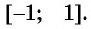
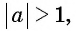
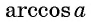
Так, выражения 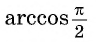
Выражение 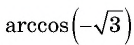
Из определения арккосинуса числа следует, что 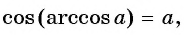
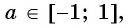
Например,
На промежутке монотонности 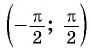
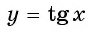
Определение Арктангенса
Определение:
Арктангенсом числа 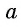
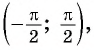
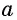
Этот угол обозначают 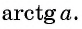
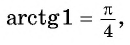
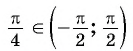
Пример №5
Вычислите:
Решение:
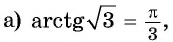
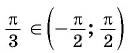
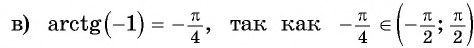
Для любого числа 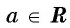
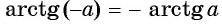
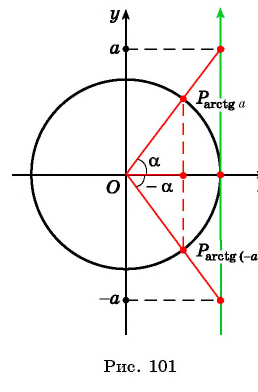
Пример №6
Найдите значение выражения
Решение:
Так как
Из определения арктангенса числа следует, что 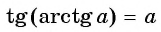
Например,
На промежутке монотонности 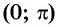
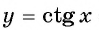
Определение Арккотангенса
Определение:
Арккотангенсом числа 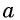
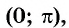
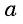
Этот угол обозначают 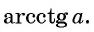
- Заказать решение задач по высшей математике
Пример №7
Вычислите:
Решение:
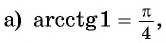
Для любого числа 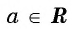
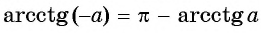
Пример №8
Найдите значение выражения
Решение:
Так как
Из определения арккотангенса числа следует, что 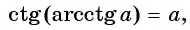
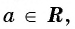
Например,
Примеры заданий и их решения
Пример №9
Верно ли, что:
Решение:
а) Верно, так как
б) верно, так как
в) неверно, так как
г) неверно, так как
Пример №10
Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим:
Пример №13
Найдите область определения выражения:
Решение:
а) По определению арксинуса числа 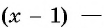
б) По определению арккосинуса числа 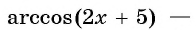
Пример №14
Найдите значение выражения:
Решение:
Пример №15
Вычислите
Решение:
Пример №16
Найдите значение выражения
Решение:
Воспользуемся формулой 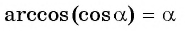
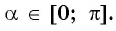
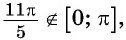
Так как
Пример №17
Найдите значение выражения
Решение:
Так как 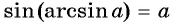
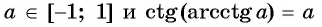
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Понятие арккосинуса
- График и свойства функции y=arccosx
- Уравнение cosx=a
- Формула арккосинуса отрицательного аргумента
- Примеры
Определение косинуса через отношение сторон прямоугольника и с помощью числовой окружности – см. §2 данного справочника.
Свойства функции y=cosx на всей области определения (xinmathbb{R}) — см. §5 данного справочника.
Определение и свойства взаимно обратных функций — см. §2 справочника для 9 класса.
п.1. Понятие арккосинуса
В записи (y=cosx) аргумент x — это значение угла (в градусах или радианах), функция y – косинус угла, действительное число в пределах [-1;1]. Т.е., по заданному углу мы находим косинус.
Можно поставить обратную задачу: по заданному косинусу найти угол. Но одному значению косинуса соответствует бесконечное количество углов. Например, если (cosx=1), то (x=2pi k, kinmathbb{Z}); (cosx=0), то (x=fracpi2+pi k, kinmathbb{Z}) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x отрезком, на котором косинус принимает все значения из [-1;1], но только один раз: (0leq xleq pi) (верхняя половина числовой окружности).
Арккосинусом числа (a left( |a|leq 1 right) ) называется такое число (xin[0;pi]), косинус которого равен (a). $$ begin{cases} arccosa=x\ |a|leq 1 end{cases} Leftrightarrow begin{cases} cosx=a\ 0leq xleq pi end{cases} $$
Например:
(arccosfrac12=fracpi3, arccosleft(-frac{sqrt{3}}{2}right)=frac{5pi}{6})
(arccos2) – не существует, т.к. 2> 1
п.2. График и свойства функции y=arccosx

1. Область определения (-1leq xleq1).
2. Функция ограничена сверху и снизу (0leq arccosxleq pi). Область значений (yin[0;pi])
3. Максимальное значение (y_{max}=pi) достигается в точке x =-1
Минимальное значение (y_{min}=0) достигается в точке x =1
4. Функция убывает на области определения.
5. Функция непрерывна на области определения.
п.3. Уравнение cosx=a
 |
Значениями арккосинуса могут быть только углы от 0 до π (180°). А как выразить другие углы через арккосинус?
Углы в нижней части числовой окружности записывают через отрицательный арккосинус. А углы, которые превышают π по модулю, записывают через сумму арккосинуса и величины, которая ‘не помещается» в область значений арккосинуса. |
Например:
1) Решим уравнение (cosx=frac12).
Найдем точку (frac12) в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках, соответствующих углам (pmfracpi3) — это базовые корни.
Если взять верхний корень (fracpi3) и прибавить к нему полный оборот (fracpi3+2pi=frac{7pi}{3}), косинус полученного угла (cosfrac{7pi}{3}=frac12), т.е. (frac{7pi}{3}) также является корнем уравнения. Корнями будут и все другие углы вида (fracpi3+2pi k) (с любым количеством добавленных или вычтенных полных оборотов). Аналогично, корнями будут все углы вида (-fracpi3+2pi k).
Получаем ответ: (x=pmfracpi3+2pi k)
Заметим, что полученный ответ является записью вида
(x=pm arccosfrac12+2pi k)
А т.к. арккосинус для (frac12) точно известен и равен (fracpi3), то мы его и пишем в ответе.
Но так бывает далеко не всегда.
2) Решим уравнение (cosx=0,8)
 |
Найдем точку 0,8 в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению верхняя точка – это угол, равный arccos0,8. Тогда нижняя точка – это тот же угол, но отложенный в отрицательном направлении обхода числовой окружности, т.е. (–arccos0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: (x=pm arccos0,8+2pi k) |
В общем случае:
Если (|a|leq 1), то уравнение (cosx=a) имеет решения $$ x=pm arccosa+2pi k, kinmathbb{Z} $$ Если (|a|gt 1) уравнение решений не имеет.
п.4. Формула арккосинуса отрицательного аргумента
Докажем полезную на практике формулу для (arccos(-a)).
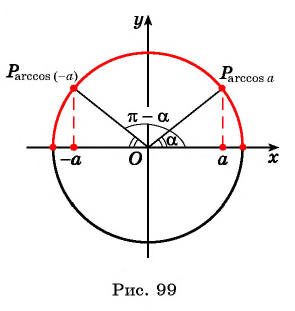
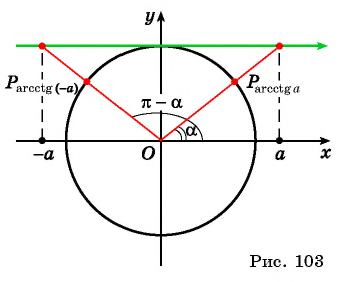
 |
По построению: $$ begin{cases} angle DA’O=angle BAO=angle CAO=90^{circ}\ OD=OB=OC=1\ OA’=OA=a end{cases} Rightarrow $$ (по катету и гипотенузе) begin{gather*} Delta DA’O=Delta BAO=Delta CAORightarrow\ Rightarrow angle DOC=angle A’OA-alpha+alpha=angle A’OA=180^{circ}=pi\ -arccosa+pi=arccos(-a) end{gather*} |
$$ arccos(-a)=pi-arccosa $$
Внимание! (arccos(-a)ne -arccosa)
Арккосинус (и арккотангенс) ни чётный, ни нечётный, в отличие от нечётного арксинуса (и арктангенса).
п.5. Примеры
Пример 1. Найдите функцию, обратную арккосинусу. Постройте графики арккосинуса и найденной функции в одной системе координат.
Для (y=arccosx) область определения (-1leq xleq 1), область значений (0leq yleq pi).
Обратная функция (y=cosx) должна иметь ограниченную область определения (0leq xleq pi) и область значений (-1leq yleq 1).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
Пример 3. Запишите в порядке возрастания: $$ arccos0,8; arccos(-0,5); arccosfracpi7 $$
 |
Способ 1. Решение с помощью числовой окружности
Отмечаем на оси косинусов (ось OX) точки с абсциссами 0,8; -0,5; (fracpi7approx 0,45) |
 |
Способ 2. Решение с помощью графика (y=arccosx)
Отмечаем на оси OX аргументы 0,8; -0,5; (fracpi7approx 0,45). Восстанавливаем перпендикуляры на кривую, отмечаем точки пересечения. Из точек пересечения с кривой восстанавливаем перпендикуляры на ось OY — получаем значения арккосинусов по возрастанию: $$ arccos0,8lt arccosfracpi7lt arccos(-0,5) $$ |
| Способ 3. Аналитический Арккосинус – функция убывающая: чем больше аргумент, тем меньше функция. Поэтому располагаем данные в условии аргументы по убыванию: 0,8; (fracpi7); -0,5. И записываем арккосинусы по возрастанию: (arccos0,8lt arccosfracpi7lt arccos(-0,5)) |
Пример 4*. Решите уравнения:
(a) arccos(x^2-3x+3)=0) begin{gather*} x^2-3x+3=cos0=1\ x^2-3x+2=0\ (x-2)(x-1)=0\ x_1=1, x_2=2 end{gather*} Ответ: {1; 2}
(б) arccos^2x-arccosx-6=0)
( text{ОДЗ:} -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: $$ t^2-t-6=0Rightarrow (t-3)(t+2)=0Rightarrow left[ begin{array} {l l} t_1=3\ t_2=-2lt 0 — text{не подходит} end{array} right. $$ Возвращаемся к исходной переменной: begin{gather*} arccosx=3\ x=cos3 end{gather*} Ответ: cos3
(в) arccos^2x-pi arccosx+frac{2pi^2}{9}=0)
( text{ОДЗ:} -1leq xleq 1 )
Замена переменных: (t=arccos x, 0leq tleq pi)
Решаем квадратное уравнение: begin{gather*} t^2-pi t+frac{2pi^2}{9}=0\ D=(pi^2)-4cdot frac{2pi^2}{9}=frac{pi^2}{9}, sqrt{D}=fracpi3\ left[ begin{array} {l l} t_1=frac{pi-fracpi3}{2}=fracpi3\ t_2=frac{pi+fracpi3}{2}=frac{2pi}{3} end{array} right. Rightarrow left[ begin{array} {l l} arccosx_1=fracpi3\ arccosx_2=frac{2pi}{3} end{array} right. Rightarrow left[ begin{array} {l l} x_1=cosleft(fracpi3right)=frac12\ x_2=cosleft(frac{2pi}{3}right)=-frac12 end{array} right. end{gather*} Ответ: (left{pmfrac12right})
Арксинус, арккосинус, арктангенс и арккотангенс – начальные сведения
Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.
В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.
Навигация по странице.
Определения, обозначения, примеры
Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.
Арксинус, арккосинус, арктангенс и арккотангенс как угол
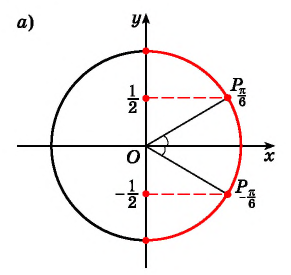
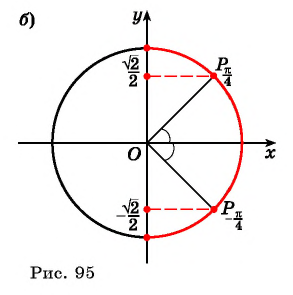
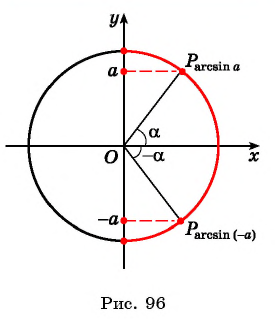
Пусть про угол альфа α известно лишь то, что его синус равен числу 1/2 , то есть, sinα=1/2 . Последнее равенство определяет угол α неоднозначно, так как ему удовлетворяет бесконечное множество углов α=(−1) k ·30°+180°·k ( α=(−1) k ·π/6+π·k ), где k∈Z . Однако, если потребовать, чтобы величина угла α в градусах принадлежала отрезку [−90, 90] (в радианах – отрезку [−π/2, π/2] ), то равенство sinα=1/2 будет определять угол альфа однозначно. При этом условии равенству удовлетворяет единственный угол в 30 градусов ( π/6 радианов).
Вообще, равенство sinα=a (не путайте a и альфа: a и α ) при любом числе a∈[−1, 1] и условии −90°≤α≤90° ( −π/2≤α≤π/2 ) определяет единственный угол α . Этот угол называют арксинусом числа a .
Арксинус числа a∈[−1, 1] – это угол −90°≤α≤90° ( −π/2≤α≤π/2 ), синус которого равен a .
Аналогично определяются арккосинус, арктангенс и арккотангенс.
Арккосинус числа a∈[−1, 1] – это угол 0°≤α≤180° ( 0≤α≤π ), косинус которого равен a .
Арктангенс числа a∈(−∞, +∞) – это угол −90° ( −π/2 ), тангенс которого равен a .
Арккотангенс числа a∈(−∞, +∞) – это угол 0° ( 0 ), котангенс которого равен a .
Для записи арксинуса, арккосинуса, арктангенса и арккотангенса приняты следующие обозначения: arcsin , arccos , arctg и arcctg . То есть, арксинус числа a можно записать как arcsin a , арккосинус, арктангенс и арккотангенс числа a запишутся соответственно как arccos a , arctg a и arcctg a .
Также можно встретить обозначения arctan и arccot , они являются другой формой обозначения арктангенса и арккотангенса, которая принята в англоязычной литературе. Мы же арктангенс и арккотангенс будем обозначать как arctg и arcctg .
В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:
arcsin a , a∈[−1, 1] , есть такой угол α , что −90°≤α≤90° ( −π/2≤α≤π/2 ) и sinα=a ;
arccos a , a∈[−1, 1] , есть такой угол α , что 0°≤α≤180° ( 0≤α≤π ) и cosα=a ;
arctg a , a∈(−∞, +∞) , есть такой угол α , что −90° ( −π/2 ) и tgα=a ;
arcctg a , a∈(−∞, +∞) , есть такой угол α , что 0° ( 0 ) и ctgα=a .
Подчеркнем, что арксинус и арккосинус числа определен для чисел, принадлежащих отрезку [−1, 1] , для остальных чисел арксинус и арккосинус не определен. Например, не имеет смысла запись arcsin2 . Аналогично не определен арксинус пяти, арксинус минус корня из трех, арккосинус семи целых двух третьих и арккосинус минус пи, так как числа 2 , 5 , , −π выходят за пределы числового отрезка от −1 до 1 . В свою очередь записи arctg a и arcctg a имеют смысл для любого действительного числа a , например, имеют смысл записи arctg0 , arctg(−500,2) , arcctg(6·π+1) и т.п.
Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.
Начнем с примеров арксинуса. Определение арксинуса позволяет утверждать, что угол π/3 является арксинусом числа , то есть, (здесь и α=π/3 ). Действительно, число принадлежит отрезку [−1, 1] , угол π/3 лежит в пределах от −π/2 до π/2 и . Приведем еще несколько примеров арксинуса числа: arcsin(−1)=−90° , arcsin(0,5)=π/6 , .
А вот π/10 не является арксинусом 1/2 , так как sin(π/10)≠1/2 . Еще пример: несмотря на то, что синус 270 градусов равен −1 , угол 270 градусов не является арксинусом минус единицы, так как 270 градусов не является углом в пределах от −90 до 90 градусов. Более того, угол 270 градусов вообще не может быть арксинусом какого-либо числа, так как арксинус числа должен лежать в пределах от −90 до 90 градусов.
Для полноты картины приведем примеры арккосинуса, арктангенса и арккотангенса числа. Например, угол 0 радианов является арккосинусом единицы, то есть, arccos1=0 (так как выполняются все условия из определения арккосинуса: число 1 принадлежит отрезку от −1 до 1 , угол нуль радианов лежит в пределах от нуля до пи включительно и cos0=1 ). Аналогично, угол π/2 есть арккосинус нуля: arccos0=π/2 . По определению арктангенса числа arctg(−1)=−π/4 или arctg(−1)=−45° . Арктангенс корня из трех равен 60 градусам ( π/3 рад). А из определения арккотангенса можно заключить, что arcctg0=π/2 , так как угол π/2 лежит в рамках от 0 до пи и ctg(π/2)=0 .
Подобный подход к определению арксинуса, арккосинуса, арктангенса и арккотангенса описан в учебнике Кочеткова [1, с. 260-278] .
Арксинус, арккосинус, арктангенс и арккотангенс как число
Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.
Арксинусом числа a∈[−1, 1] называется такое число t∈[−π/2, π/2] , синус которого равен a .
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
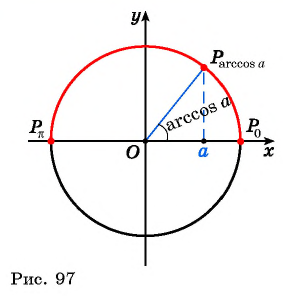
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Можно утверждать, что косинус – это ф-ция, которая ставит каждому углу в соответствие некоторую координату х. Теперь предположим, что нам известна эта координата (пусть она будет равна величине а), и по ней надо определить значение угла. Отложим на оси Ох отрезок длиной а, проведем через него вертикальную прямую и отметим ее точки пересечения с единичной окружностью. Если – 1 1 либо а n ,будет равно единице, и мы получим первую серию. Если же n – нечетное число, то, то выражение (– 1) n окажется равным (– 1), и мы получим вторую серию.
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Ответ: 7π/3 и 8π/3.
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
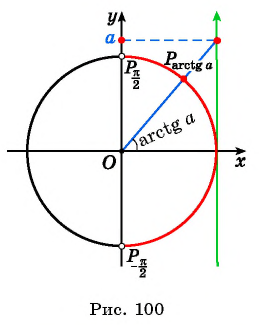
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
в р а д и а н а х
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
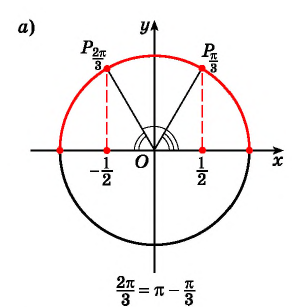
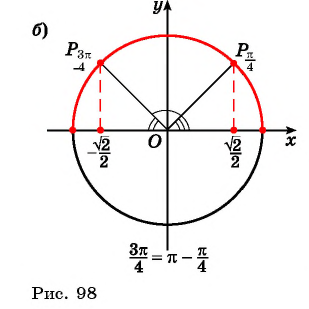
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
в р а д и а н а х
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
http://100urokov.ru/predmety/urok-4-prostejshaya-trigonometriya
http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-arksinusa-arkkosinusa-arktan/
Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
| arccos(1) = 0° | arccos(-0.5) = 120° | arccos(-0.5) = 240° |
| arccos(0.9998476952) = 1° | arccos(-0.5150380749) = 121° | arccos(-0.4848096202) = 241° |
| arccos(0.999390827) = 2° | arccos(-0.5299192642) = 122° | arccos(-0.4694715628) = 242° |
| arccos(0.9986295348) = 3° | arccos(-0.544639035) = 123° | arccos(-0.4539904997) = 243° |
| arccos(0.9975640503) = 4° | arccos(-0.5591929035) = 124° | arccos(-0.4383711468) = 244° |
| arccos(0.9961946981) = 5° | arccos(-0.5735764364) = 125° | arccos(-0.4226182617) = 245° |
| arccos(0.9945218954) = 6° | arccos(-0.5877852523) = 126° | arccos(-0.4067366431) = 246° |
| arccos(0.9925461516) = 7° | arccos(-0.6018150232) = 127° | arccos(-0.3907311285) = 247° |
| arccos(0.9902680687) = 8° | arccos(-0.6156614753) = 128° | arccos(-0.3746065934) = 248° |
| arccos(0.9876883406) = 9° | arccos(-0.629320391) = 129° | arccos(-0.3583679495) = 249° |
| arccos(0.984807753) = 10° | arccos(-0.6427876097) = 130° | arccos(-0.3420201433) = 250° |
| arccos(0.9816271834) = 11° | arccos(-0.656059029) = 131° | arccos(-0.3255681545) = 251° |
| arccos(0.9781476007) = 12° | arccos(-0.6691306064) = 132° | arccos(-0.3090169944) = 252° |
| arccos(0.9743700648) = 13° | arccos(-0.6819983601) = 133° | arccos(-0.2923717047) = 253° |
| arccos(0.9702957263) = 14° | arccos(-0.6946583705) = 134° | arccos(-0.2756373558) = 254° |
| arccos(0.9659258263) = 15° | arccos(-0.7071067812) = 135° | arccos(-0.2588190451) = 255° |
| arccos(0.9612616959) = 16° | arccos(-0.7193398003) = 136° | arccos(-0.2419218956) = 256° |
| arccos(0.956304756) = 17° | arccos(-0.7313537016) = 137° | arccos(-0.2249510543) = 257° |
| arccos(0.9510565163) = 18° | arccos(-0.7431448255) = 138° | arccos(-0.2079116908) = 258° |
| arccos(0.9455185756) = 19° | arccos(-0.7547095802) = 139° | arccos(-0.1908089954) = 259° |
| arccos(0.9396926208) = 20° | arccos(-0.7660444431) = 140° | arccos(-0.1736481777) = 260° |
| arccos(0.9335804265) = 21° | arccos(-0.7771459615) = 141° | arccos(-0.156434465) = 261° |
| arccos(0.9271838546) = 22° | arccos(-0.7880107536) = 142° | arccos(-0.139173101) = 262° |
| arccos(0.9205048535) = 23° | arccos(-0.79863551) = 143° | arccos(-0.1218693434) = 263° |
| arccos(0.9135454576) = 24° | arccos(-0.8090169944) = 144° | arccos(-0.1045284633) = 264° |
| arccos(0.906307787) = 25° | arccos(-0.8191520443) = 145° | arccos(-0.08715574275) = 265° |
| arccos(0.8987940463) = 26° | arccos(-0.8290375726) = 146° | arccos(-0.06975647374) = 266° |
| arccos(0.8910065242) = 27° | arccos(-0.8386705679) = 147° | arccos(-0.05233595624) = 267° |
| arccos(0.8829475929) = 28° | arccos(-0.8480480962) = 148° | arccos(-0.0348994967) = 268° |
| arccos(0.8746197071) = 29° | arccos(-0.8571673007) = 149° | arccos(-0.01745240644) = 269° |
| arccos(0.8660254038) = 30° | arccos(-0.8660254038) = 150° | arccos(0) = 270° |
| arccos(0.8571673007) = 31° | arccos(-0.8746197071) = 151° | arccos(0.01745240644) = 271° |
| arccos(0.8480480962) = 32° | arccos(-0.8829475929) = 152° | arccos(0.0348994967) = 272° |
| arccos(0.8386705679) = 33° | arccos(-0.8910065242) = 153° | arccos(0.05233595624) = 273° |
| arccos(0.8290375726) = 34° | arccos(-0.8987940463) = 154° | arccos(0.06975647374) = 274° |
| arccos(0.8191520443) = 35° | arccos(-0.906307787) = 155° | arccos(0.08715574275) = 275° |
| arccos(0.8090169944) = 36° | arccos(-0.9135454576) = 156° | arccos(0.1045284633) = 276° |
| arccos(0.79863551) = 37° | arccos(-0.9205048535) = 157° | arccos(0.1218693434) = 277° |
| arccos(0.7880107536) = 38° | arccos(-0.9271838546) = 158° | arccos(0.139173101) = 278° |
| arccos(0.7771459615) = 39° | arccos(-0.9335804265) = 159° | arccos(0.156434465) = 279° |
| arccos(0.7660444431) = 40° | arccos(-0.9396926208) = 160° | arccos(0.1736481777) = 280° |
| arccos(0.7547095802) = 41° | arccos(-0.9455185756) = 161° | arccos(0.1908089954) = 281° |
| arccos(0.7431448255) = 42° | arccos(-0.9510565163) = 162° | arccos(0.2079116908) = 282° |
| arccos(0.7313537016) = 43° | arccos(-0.956304756) = 163° | arccos(0.2249510543) = 283° |
| arccos(0.7193398003) = 44° | arccos(-0.9612616959) = 164° | arccos(0.2419218956) = 284° |
| arccos(0.7071067812) = 45° | arccos(-0.9659258263) = 165° | arccos(0.2588190451) = 285° |
| arccos(0.6946583705) = 46° | arccos(-0.9702957263) = 166° | arccos(0.2756373558) = 286° |
| arccos(0.6819983601) = 47° | arccos(-0.9743700648) = 167° | arccos(0.2923717047) = 287° |
| arccos(0.6691306064) = 48° | arccos(-0.9781476007) = 168° | arccos(0.3090169944) = 288° |
| arccos(0.656059029) = 49° | arccos(-0.9816271834) = 169° | arccos(0.3255681545) = 289° |
| arccos(0.6427876097) = 50° | arccos(-0.984807753) = 170° | arccos(0.3420201433) = 290° |
| arccos(0.629320391) = 51° | arccos(-0.9876883406) = 171° | arccos(0.3583679495) = 291° |
| arccos(0.6156614753) = 52° | arccos(-0.9902680687) = 172° | arccos(0.3746065934) = 292° |
| arccos(0.6018150232) = 53° | arccos(-0.9925461516) = 173° | arccos(0.3907311285) = 293° |
| arccos(0.5877852523) = 54° | arccos(-0.9945218954) = 174° | arccos(0.4067366431) = 294° |
| arccos(0.5735764364) = 55° | arccos(-0.9961946981) = 175° | arccos(0.4226182617) = 295° |
| arccos(0.5591929035) = 56° | arccos(-0.9975640503) = 176° | arccos(0.4383711468) = 296° |
| arccos(0.544639035) = 57° | arccos(-0.9986295348) = 177° | arccos(0.4539904997) = 297° |
| arccos(0.5299192642) = 58° | arccos(-0.999390827) = 178° | arccos(0.4694715628) = 298° |
| arccos(0.5150380749) = 59° | arccos(-0.9998476952) = 179° | arccos(0.4848096202) = 299° |
| arccos(0.5) = 60° | arccos(-1) = 180° | arccos(0.5) = 300° |
| arccos(0.4848096202) = 61° | arccos(-0.9998476952) = 181° | arccos(0.5150380749) = 301° |
| arccos(0.4694715628) = 62° | arccos(-0.999390827) = 182° | arccos(0.5299192642) = 302° |
| arccos(0.4539904997) = 63° | arccos(-0.9986295348) = 183° | arccos(0.544639035) = 303° |
| arccos(0.4383711468) = 64° | arccos(-0.9975640503) = 184° | arccos(0.5591929035) = 304° |
| arccos(0.4226182617) = 65° | arccos(-0.9961946981) = 185° | arccos(0.5735764364) = 305° |
| arccos(0.4067366431) = 66° | arccos(-0.9945218954) = 186° | arccos(0.5877852523) = 306° |
| arccos(0.3907311285) = 67° | arccos(-0.9925461516) = 187° | arccos(0.6018150232) = 307° |
| arccos(0.3746065934) = 68° | arccos(-0.9902680687) = 188° | arccos(0.6156614753) = 308° |
| arccos(0.3583679495) = 69° | arccos(-0.9876883406) = 189° | arccos(0.629320391) = 309° |
| arccos(0.3420201433) = 70° | arccos(-0.984807753) = 190° | arccos(0.6427876097) = 310° |
| arccos(0.3255681545) = 71° | arccos(-0.9816271834) = 191° | arccos(0.656059029) = 311° |
| arccos(0.3090169944) = 72° | arccos(-0.9781476007) = 192° | arccos(0.6691306064) = 312° |
| arccos(0.2923717047) = 73° | arccos(-0.9743700648) = 193° | arccos(0.6819983601) = 313° |
| arccos(0.2756373558) = 74° | arccos(-0.9702957263) = 194° | arccos(0.6946583705) = 314° |
| arccos(0.2588190451) = 75° | arccos(-0.9659258263) = 195° | arccos(0.7071067812) = 315° |
| arccos(0.2419218956) = 76° | arccos(-0.9612616959) = 196° | arccos(0.7193398003) = 316° |
| arccos(0.2249510543) = 77° | arccos(-0.956304756) = 197° | arccos(0.7313537016) = 317° |
| arccos(0.2079116908) = 78° | arccos(-0.9510565163) = 198° | arccos(0.7431448255) = 318° |
| arccos(0.1908089954) = 79° | arccos(-0.9455185756) = 199° | arccos(0.7547095802) = 319° |
| arccos(0.1736481777) = 80° | arccos(-0.9396926208) = 200° | arccos(0.7660444431) = 320° |
| arccos(0.156434465) = 81° | arccos(-0.9335804265) = 201° | arccos(0.7771459615) = 321° |
| arccos(0.139173101) = 82° | arccos(-0.9271838546) = 202° | arccos(0.7880107536) = 322° |
| arccos(0.1218693434) = 83° | arccos(-0.9205048535) = 203° | arccos(0.79863551) = 323° |
| arccos(0.1045284633) = 84° | arccos(-0.9135454576) = 204° | arccos(0.8090169944) = 324° |
| arccos(0.08715574275) = 85° | arccos(-0.906307787) = 205° | arccos(0.8191520443) = 325° |
| arccos(0.06975647374) = 86° | arccos(-0.8987940463) = 206° | arccos(0.8290375726) = 326° |
| arccos(0.05233595624) = 87° | arccos(-0.8910065242) = 207° | arccos(0.8386705679) = 327° |
| arccos(0.0348994967) = 88° | arccos(-0.8829475929) = 208° | arccos(0.8480480962) = 328° |
| arccos(0.01745240644) = 89° | arccos(-0.8746197071) = 209° | arccos(0.8571673007) = 329° |
| arccos(0) = 90° | arccos(-0.8660254038) = 210° | arccos(0.8660254038) = 330° |
| arccos(-0.01745240644) = 91° | arccos(-0.8571673007) = 211° | arccos(0.8746197071) = 331° |
| arccos(-0.0348994967) = 92° | arccos(-0.8480480962) = 212° | arccos(0.8829475929) = 332° |
| arccos(-0.05233595624) = 93° | arccos(-0.8386705679) = 213° | arccos(0.8910065242) = 333° |
| arccos(-0.06975647374) = 94° | arccos(-0.8290375726) = 214° | arccos(0.8987940463) = 334° |
| arccos(-0.08715574275) = 95° | arccos(-0.8191520443) = 215° | arccos(0.906307787) = 335° |
| arccos(-0.1045284633) = 96° | arccos(-0.8090169944) = 216° | arccos(0.9135454576) = 336° |
| arccos(-0.1218693434) = 97° | arccos(-0.79863551) = 217° | arccos(0.9205048535) = 337° |
| arccos(-0.139173101) = 98° | arccos(-0.7880107536) = 218° | arccos(0.9271838546) = 338° |
| arccos(-0.156434465) = 99° | arccos(-0.7771459615) = 219° | arccos(0.9335804265) = 339° |
| arccos(-0.1736481777) = 100° | arccos(-0.7660444431) = 220° | arccos(0.9396926208) = 340° |
| arccos(-0.1908089954) = 101° | arccos(-0.7547095802) = 221° | arccos(0.9455185756) = 341° |
| arccos(-0.2079116908) = 102° | arccos(-0.7431448255) = 222° | arccos(0.9510565163) = 342° |
| arccos(-0.2249510543) = 103° | arccos(-0.7313537016) = 223° | arccos(0.956304756) = 343° |
| arccos(-0.2419218956) = 104° | arccos(-0.7193398003) = 224° | arccos(0.9612616959) = 344° |
| arccos(-0.2588190451) = 105° | arccos(-0.7071067812) = 225° | arccos(0.9659258263) = 345° |
| arccos(-0.2756373558) = 106° | arccos(-0.6946583705) = 226° | arccos(0.9702957263) = 346° |
| arccos(-0.2923717047) = 107° | arccos(-0.6819983601) = 227° | arccos(0.9743700648) = 347° |
| arccos(-0.3090169944) = 108° | arccos(-0.6691306064) = 228° | arccos(0.9781476007) = 348° |
| arccos(-0.3255681545) = 109° | arccos(-0.656059029) = 229° | arccos(0.9816271834) = 349° |
| arccos(-0.3420201433) = 110° | arccos(-0.6427876097) = 230° | arccos(0.984807753) = 350° |
| arccos(-0.3583679495) = 111° | arccos(-0.629320391) = 231° | arccos(0.9876883406) = 351° |
| arccos(-0.3746065934) = 112° | arccos(-0.6156614753) = 232° | arccos(0.9902680687) = 352° |
| arccos(-0.3907311285) = 113° | arccos(-0.6018150232) = 233° | arccos(0.9925461516) = 353° |
| arccos(-0.4067366431) = 114° | arccos(-0.5877852523) = 234° | arccos(0.9945218954) = 354° |
| arccos(-0.4226182617) = 115° | arccos(-0.5735764364) = 235° | arccos(0.9961946981) = 355° |
| arccos(-0.4383711468) = 116° | arccos(-0.5591929035) = 236° | arccos(0.9975640503) = 356° |
| arccos(-0.4539904997) = 117° | arccos(-0.544639035) = 237° | arccos(0.9986295348) = 357° |
| arccos(-0.4694715628) = 118° | arccos(-0.5299192642) = 238° | arccos(0.999390827) = 358° |
| arccos(-0.4848096202) = 119° | arccos(-0.5150380749) = 239° | arccos(0.9998476952) = 359° |