Как найти чему равен х в алгоритме - Исправление недочетов и поиск решений вместе с Examum.ru

Если дать определение схеме, можно отметить основной момент: в первую очередь подразумевается абстракция какого-нибудь процесса (системы), при которой наиболее важные части отображаются наглядно (визуально). Схемы использовались на протяжении всей истории человечества: это и чертежи пирамид, и карты сухопутных и морских путей, и принципиальные электрические схемы.

Те же мореплаватели, создавая карты, делали это в соответствии с единой системой обозначений — это позволяло обмениваться информацией друг с другом. То же самое справедливо и для визуального отображения схем алгоритмов — существуют правила, единые обозначения и стандарты, регламентирующие их применение. В России это ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем», который близок к международному стандарту ISO 5807:1985.

Главные элементы блок-схем алгоритмов

Прежде чем продолжить, стоит дать определение блок-схемы в соответствии со стандартом — речь идёт о совокупности символов, которые отвечают этапам работы алгоритма, причём эти символы имеют соединяющие линии:
— пунктирную — для соединения с комментарием;
— сплошную — отображает зависимости по управлению, допускается наличие на ней стрелки. В соответствии со стандартом составитель может не указывать стрелку, если дуга направляется сверху вниз или слева направо.

Также существуют и дополнительные виды линий, которые применяются, когда надо дать описание блок-схемам параллельных алгоритмов, однако в этой статье мы их рассматривать не будем, как и ряд других дополнительных спецсимволов.

В таблице ниже дан перечень основных символов, используемых при описании алгоритмов:

Задача и блок-схема алгоритма

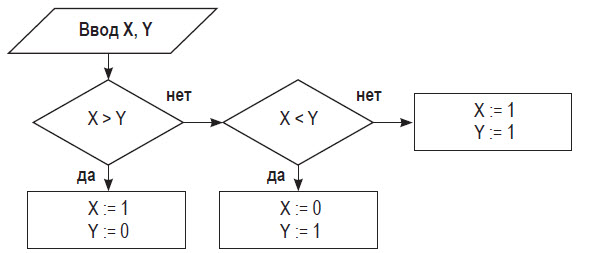
На картинке ниже дан алгоритм в виде схемы. В нем мы видим оператор присваивания :=, то есть X := 1 будет означать, что переменная Х примет значение 1. По результату алгоритмических действий надо определить итог работы представленного алгоритма, используя следующие входные данные: Х = 7, Y = 12.

Схема этого алгоритма и решение задачи будут выглядеть следующим образом:

Смотрим, как следует решать подобное задание:
1. Блок ввода данных определяет исходные значения Х и Y (в соответствии с условием это 7 и 12).
2. В первом блоке значения Х и Y сравниваются. Так как условие не является верным (7 < 12), осуществляется переход по линии с пометкой «нет».
3. Второй блок служит для второго сравнения — оно верное, в результате чего следующее действие — это переход по линии с отметкой «да».
4. Следующий этап является заключительным, то есть происходит вычисление результата работы алгоритма. По итогу всех вышеописанных действий мы получаем окончательный ответ, не требующий дополнительных вычислений: X := 0, Y := 1.

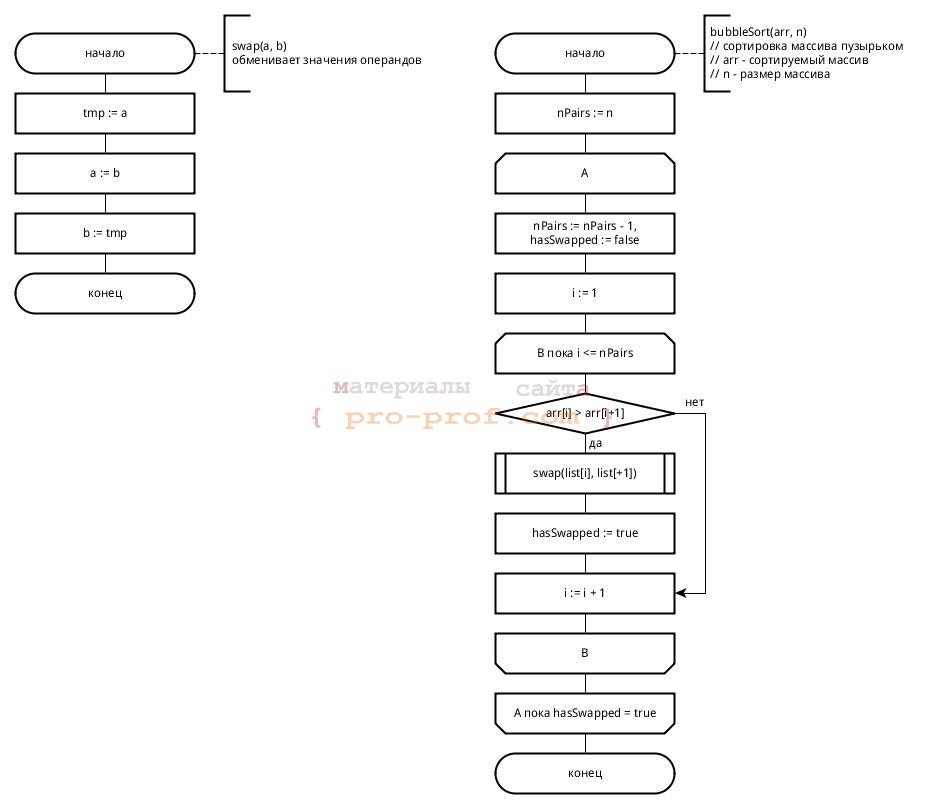
Решение алгоритма сортировки пузырьком

В этом примере давайте попробуем дать описание решению алгоритма сортировки по методу пузырьком (метод сортировки вставками). Здесь применяются 2 цикла. Во вложенном цикле осуществляется попарное сравнение элементов. Если нарушается порядок, происходит перестановка. По итогу выполнения одной итерации во внутреннем цикле, наибольший элемент будет смещён в самый конец массива. Внешний цикл будет выполняться, пока полностью весь массив не отсортируется.

На схеме отображено применение символов конца и начала цикла. Здесь условие внешнего цикла (А) проверяется в конце (с постусловием), а функционирует он до тех пор, пока переменная hasSwapped является true. Во внутреннем цикле используется предусловие для перебора пар элементов, которые сравниваются. Если они располагаются в неправильном порядке, они переставляются путём вызова внешней процедуры (swap). Для понимания назначения внешней процедуры, как и порядка следования аргументов этой процедуры, нужно оставлять комментарии. Если функция возвращает значение, то комментарий можно написать к символу-терминатору конца.

В этой статье мы постарались дать ответ, зачем нужны блок-схемы, каковы их основные элементы, как с их помощью решить алгоритмическую задачу. При подготовке материала использовались следующие источники:

• https://uchitel.pro/алгоритм-свойства-алгоритмов/;
• https://pro-prof.com/archives/1462.

Источник

§ 2.4. Основные алгоритмические конструкции

Информатика. 8 класса. Босова Л.Л. Оглавление

Ключевые слова:

следование
ветвление
повторение
линейные алгоритмы
разветвляющиеся алгоритмы
циклические алгоритмы

Человеку в жизни приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.

Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.

2.4.1. Следование. Основные алгоритмические конструкции

Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.

Графическое представление алгоритмической конструкции «следование» приведено на рис. 2.8.

Пример 1. Линейный алгоритм приготовления отвара шиповника.

Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний.

Пример 2. У исполнителя Робот есть четыре команды перемещения (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направлении. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение, обозначенное звёздочкой:

Пример 3. Дан фрагмент линейного алгоритма:

х: =2
у :=х*х
у:=у*у
х:=у*х
s:=х+у

Выясним, какое значение получит переменная s после выполнения этого фрагмента алгоритма. Для этого составим таблицу значений переменных, задействованных в алгоритме:

Составленная нами таблица значений переменных моделирует работу исполнителя этого алгоритма.

Пример 4. Некоторый исполнитель может выполнять над целыми ЧЧ0, числами кроме операций сложения, вычитания, умножения и деления ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.

Например: 5 div 2 = 2; 5 mod 2 = 1; 2 div 5 = 0; 2 mod 5 = 2.

Покажем, как с помощью этих операций можно реализовать алгоритм работы кассира, выдающего покупателю сдачу (s) наименьшим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10)рублей.

k500:=s div 500
s:=s mod 500
k100:=s div 100
s:=s mod 100
k50:=s div 50
s:=s mod 50
k10:=s div 10

Исполните алгоритм для s = 745 и s = 1864. Составьте соответствующие таблицы значений переменных.

Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

2.4.2. Ветвление. Основные алгоритмические конструкции

Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.

Блок-схема ветвления представлена на рис. 2.9. Каждая ветвь может быть любой степени сложности (рис. 2.9, а), а может вообще не содержать предписаний (рис. 2.9, б).

На алгоритмическом языке команда ветвления записывается так:

Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:

А<В — А меньше В;
А<=В — А меньше или равно В;
А=В — А равно В;
А>В — А больше В;
А>=В — А больше или равно В;
А<>В — А не равно В.

Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.

Пример 7. Алгоритм вычисления функции ?(x) = |х| для произвольного числа х.

Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.

Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.

Пример 8. Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.

Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.

Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, Б и С.

Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:

Пример 10. Алгоритм решения линейного уравнения ах + b = 0.

Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:

справа свободно
слева свободно
сверху свободно
снизу свободно
клетка чистая

справа стена
слева стена
сверху стена
снизу стена
клетка закрашена

Также Робот может действовать в зависимости от выполнения составных условий.

Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.

если справа свободно или снизу свободно
то закрасить
все
если справа стена
то влево
все
если слева стена
то вправо
все

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Алгоритмы с ветвящейся структурой» (217044). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

Повторение. Основные алгоритмические конструкции

Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.

В зависимости от способа организации повторений различают три типа циклов:

1) цикл с заданным условием продолжения работы;
2) цикл с заданным условием окончания работы;
3) цикл с заданным числом повторений.

Цикл с заданным условием продолжения работы (цикл-ПОКА, цикл с предусловием)

Логика работы этой конструкции описывается схемой, показанной на рис. 2.10.

На алгоритмическом языке эта конструкция записывается так:

нц пока <условие>
<тело цикла (последовательность действий)>
кц

Выполняется цикл-ПОКА следующим образом: 1) проверяется условие (вычисляется значение логического выражения); 2) если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу.

Пример 12. Алгоритм, по которому из всех имеющихся кирпичей отбираются целые кирпичи и складываются в машину.

алг отбор
нач
нц пока есть кирпичи
взять один кирпич
если кирпич целый
то положить кирпич в машину
иначе отложить кирпич в сторону
все
кц кон

Пример 13. Правее Робота (клетка со звёздочкой) расположен коридор неизвестной длины. Необходимо, чтобы Робот закрасил все клетки этого коридора.

Пока будет выполняться условие справа свободно, Роботу следует выполнять команды:

вправо
закрась

Соответствующий алгоритм для Робота будет иметь вид:

нц пока справа свободно
вправо
закрась
кц

Пример 14. Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления натурального числа х на натуральное число у.

Представим операцию деления как последовательные вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет равно частному от деления q, а последняя разность — остатку от деления r.

Исполним этот алгоритм для х = 23 и у = 5.

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с предусловием» (217033). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием)

Логика работы этой конструкции описывается схемой, показанной на рис. 2.11.

На алгоритмическом языке эта конструкция записывается так:

нц
<тело_цикла (последовательность действий)>
кц при <условие>

Выполняется цикл-ДО следующим образом: 1) выполняется тело цикла; 2) проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется («Нет»), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз.

Пример 15. Алгоритм по выучиванию наизусть четверостишия.

алг четверостишие
нач
нц
прочитать четверостишие по книге 1 раз
рассказать четверостишие
кц при не сделал ошибку кон

Пример 16. Вычислим значение переменной b согласно следующему алгоритму:

Составим таблицу значений переменных, задействованных в алгоритме:

Ответ: b = 255.

Пример 17. Спортсмен приступает к тренировкам по следующему графику: в первый день он должен пробежать 10 км; каждый следующий день следует увеличивать дистанцию на 10% от нормы предыдущего дня. Как только дневная норма достигнет или превысит 25 км, необходимо прекратить её увеличение и далее пробегать ежедневно ровно 25 км. Начиная с какого дня спортсмен будет пробегать 25 км?

Пусть х — количество километров, которое спортсмен пробежит в некоторый i-й день. Тогда в следующий (i + 1)-й день он пробежит х + 0,1х километров (0,1х — это 10% от х).

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с постусловием» (217037). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром)

Логика работы этой конструкции описывается схемой, показанной на рис. 2.12.

На алгоритмическом языке эта конструкция записывается так:

нц для i от i1 до i2 шаг R
<тело цикла (последовательность действий)>
кц

В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения il до конечного значения i2 с шагом R.

Выполняется цикл-ДЛЯ следующим образом: 1) параметру цикла присваивается начальное значение; 2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла на шаг и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.

Если величина шага в цикле с параметром равна единице, то шаг не указывают. Мы ограничимся рассмотрением именно таких циклов.

В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.

Пример 18. Алгоритм переправы через реку воинского отряда из пяти человек. Солдаты могут воспользоваться помощью двух мальчиков — хозяев небольшой лодки, в которой может переправиться или один солдат, или два мальчика.

алг переправа
нач
нц для i от 1 до 5
два мальчика переправляются на противоположный берег
один мальчик высаживается на берег, другой плывёт обратно
солдат переправляется через реку
мальчик возвращается на исходную позицию
кц
кон

Пример 19. Составим алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а.

По определению:

При составлении алгоритма воспользуемся единой формулой, в которой число умножений равно показателю степени:

Исполним этот алгоритм для а = 4 и n = 3.

Пример 20. Для исполнителя Робот цикл с известным числом повторений реализуется с помощью следующей конструкции:

нц <число повторений> раз
<тело цикла>
кц

Так, если правее Робота не встретится препятствий, то, выполнив приведённый ниже алгоритм, он переместится на пять клеток вправо и закрасит эти клетки:

алг
нач
нц 5 раз
вправо; закрасить
кц
кон

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Циклические алгоритмы с параметром» (217024). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

Основные алгоритмические конструкции. Самое главное

Для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения.

Повторение — алгоритмическая конструкция, представляющая собой последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию «повторение», называют циклическими или циклами. Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла. В зависимости от способа организации повторений различают три типа циклов:

1) цикл с заданным условием продолжения работы;
2) цикл с заданным условием окончания работы;
3) цикл с заданным числом повторений.

Основные алгоритмические конструкции. Вопросы и задания

2. Какие алгоритмы называются линейными?

3. Приведите пример линейного алгоритма: из повседневной жизни.

4. Запишите линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение.

5. По алгоритму восстановите формулу. a1:=1/x а2:=a1/x а3:=а2/ха4:=а3/хy:=a1+a2у:=у+а3у:=у+а4

6. Какое значение получит переменная у после выполнения фрагмента алгоритма? х:=1 у:=2*ху:=у+3 у: =у*х у:=у+4 у:=у*х у:=у+5
Восстановите формулу вычисления и для произвольного значения X.

7. Для заданного количества суток (tfh) требуется определить количество часов (h), минут (m) и секунд (с).

8. Известно, что 1 миля = 7 вёрст, 1 верста = 500 саженей, 1 сажень = 3 аршина, 1 аршин = 28 дюймов, 1 дюйм = 25,4 мм. Пользуясь этой информацией, составьте линейный алгоритм перевода расстояния X миль в километры.

9. Исходное данное — целое трёхзначное число х. Выполните для х = 125 следующий алгоритм.а:=х div 100b:=x mod 100 div 10с:=х mod 10s:=a+b+cЧем является результат s этого алгоритма?

10. Определите значение целочисленных переменных х и у после выполнения фрагмента алгоритма.
х:=336y: =8х:=х div у у:=х mod у

11. Какие алгоритмы называют разветвляющимися?

12. Приведите пример разветвляющегося алгоритма из повседневной жизни.

13. Дополните алгоритм из примера 9 так, чтобы с его помощью можно было найти наибольшую из четырёх величин А, B, С и D.

14. Составьте алгоритм, с помощью которого можно определить, существует ли треугольник с длинами сторон а, b, c.

15. Составьте алгоритм, с помощью которого можно определить, является ли треугольник с заданными длинами сторон а, b, с равносторонним.

16. Составьте алгоритм возведения чётного числа в квадрат, а нечётного — в куб.

17. Какая задача решается с помощью следующего алгоритма?

18. Составьте блок схему алгоритма определения количества чётных чисел среди заданных целых чисел А, В и С.

19. Запишите алгоритм определения принадлежности точки X отрезку [А; В] (пример с использованием комбинации из двух ветвлений.

20. Запишите алгоритм правописания приставок, начинающихся с буквы «з» («с»).

21. Известно, что 31 января 2011 года приходится на понедельник. Какие значения должны быть присвоены литерной переменной у в алгоритме, определяющем день недели для любого числа (chislo) января 2011 года?

22. Даны две точки на плоскости. Определите, какая из них находится ближе к началу координат.

23. Определите, есть ли среди цифр заданного целого трёхзначного числа одинаковые.

24. Приведите примеры циклического алгоритма.

25. Напишите алгоритм под управлением которого Робот обойдет прямоугольную область, обнесенную стеной, по периметру и закрасит угловые клетки. Размеры области неизвестны.

26. Запас рыбы в пруду оценён в А тонн. Ежегодный прирост рыбы составляет 15%. Ежегодный план отлова — В тонн. Наименьший запас рыбы составляет С тонн. (Запас ниже С тонн уже не восстанавливается.) Составьте блок-схему алгоритма для подсчёта количества лет, в течение которых можно выдерживать заданный план.

27. Дана последовательность 5, 9, 13, 17, … . Составьте блок-схему алгоритма для подсчёта числа слагаемых, сумма которых равна 324.

28. Составьте алгоритм для определения количества цифр в записи произвольного натурального числа.

29. Сумма 10 ООО рублей положена в сберегательный банк, при этом прирост составляет 5% годовых. Составьте алгоритм, определяющий, через какой промежуток времени первоначальная сумма увеличится в два раза.

30. Одноклеточная амёба каждые три часа делится на 2 клетки. Составьте алгоритм вычисления времени, через которое будет X амёб.

31. Определите значения переменных n и m после выполнения алгоритма

§ 2.3. Объекты алгоритмов

§ 2.4. Основные алгоритмические конструкции

§ 3.1. Общие сведения о языке программирования Паскаль

Источник

Решение задач на выполнение алгоритма

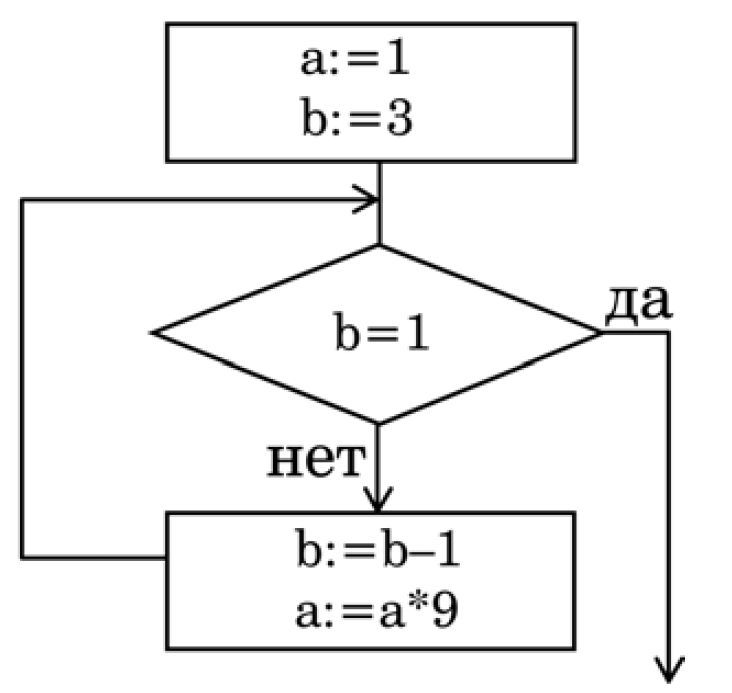
Задача №1 Определите значение переменной а после выполнения фрагмента алгоритма:

Примечание: знаком * обозначено умножение,
знаком := обозначена операция присваивания.
Решение задачи №1 Последовательно выпишем значения переменных в ходе цикла, пока переменная b не станет равной 1 .

Шаг 1.	b=b-1=3-1=2 a=a9=19=9
Шаг 2.	b=b-1=2-1=1 a=a9=99=81

Так как после второго шага переменная b равна 1, то по условию «b=1», цикл завершён.
Ответ: Переменная а равна 81.

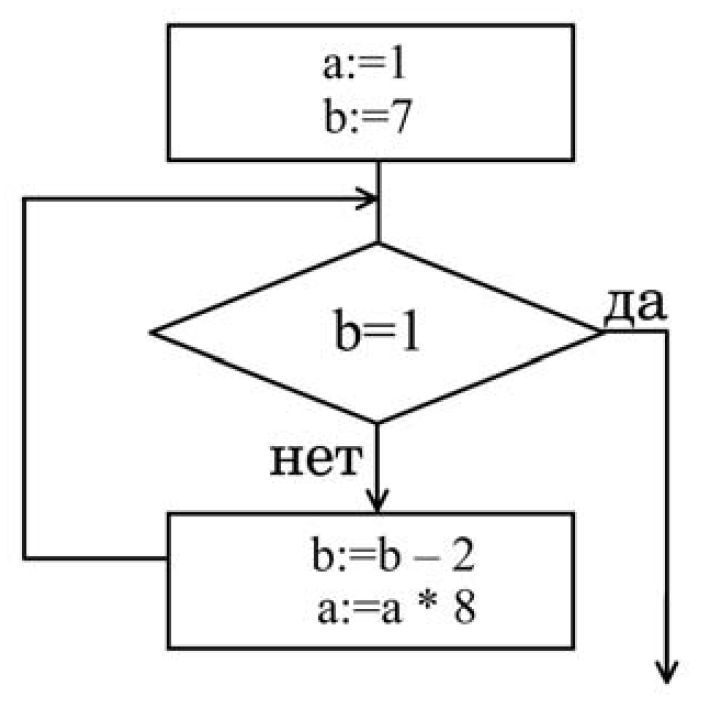
Задача №2

Примечание: знаком * обозначено умножение,
знаком := обозначена операция присваивания.

Решение задачи №2 Последовательно выпишем значения переменных в ходе цикла, пока переменная b не станет равной 1 .

Шаг 1.	b=b-2=7-2=5 a=a8=18=8
Шаг 2.	b=b-2=5-2=3 a=a8=88=64
Шаг 3.	b=b-2=3-2=1 а=a8=648=512

Так как после второго шага переменная b равна 1, то по условию «b=1», цикл завершён.
Ответ: Переменная а равна 512.

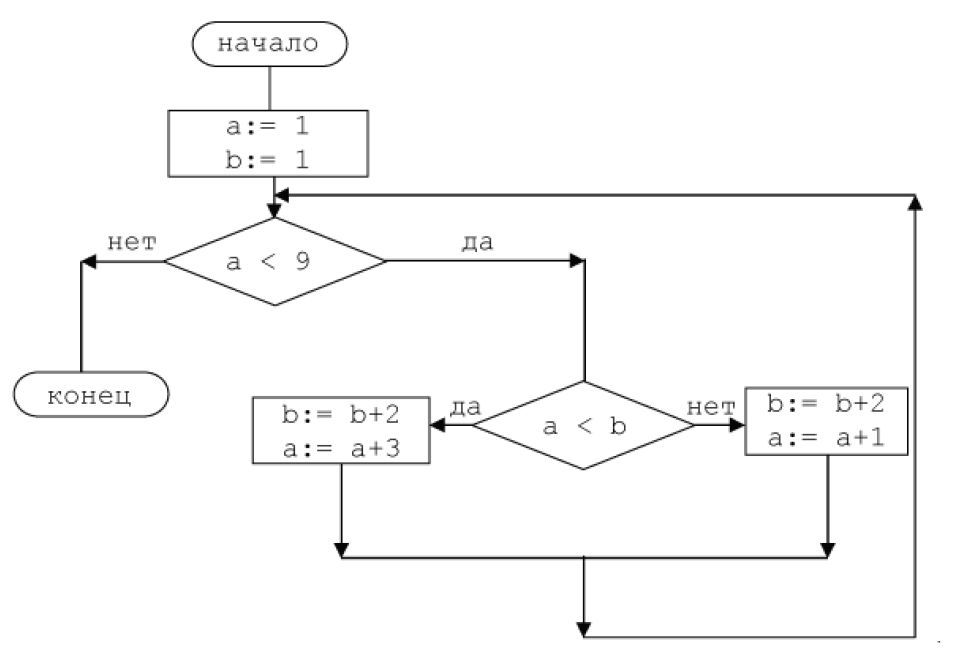
Задача №3

Решение задачи №3 Последовательно выпишем значения переменных в ходе цикла, пока не выполнится следующее условие «а<9» .

Шаг 1.	Проверяем условие «а<b», условия не выполняется (идем по стрелки «нет»). b=b+2=1+2=3 a=a+1=1+1=2
Шаг 2.	Проверяем условие «а<b», условия выполняется (идем по стрелки «да»). b=b+2=3+2=5 a=a+3=2+3=5
Шаг 3.	Проверяем условие «а<b», условия не выполняется (идем по стрелки «нет»). b=b+2=5+2=7 a=a+1=5+1=6
Шаг 4.	Проверяем условие «а<b», условия выполняется (идем по стрелки «да»). b=b+2=7+2=9 a=a+3=6+3=9

Так как после четвертого шага переменная а равна 9, то по условию «а<9» , цикл завершён.
Ответ: Переменная b равна 9.

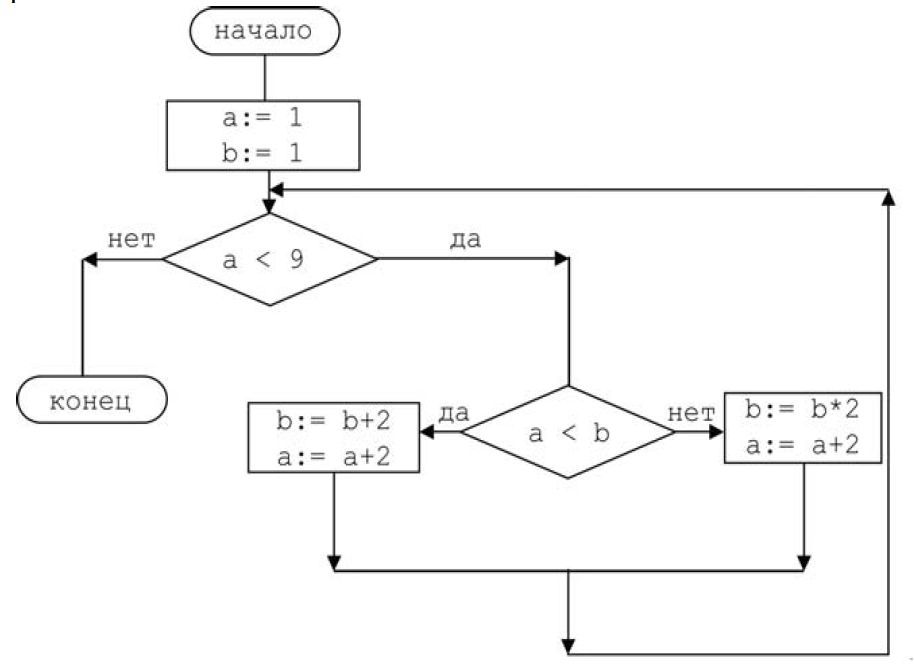
Задача №4 Определите значение переменной b после выполнения фрагмента алгоритма:

Решение задачи №4 Последовательно выпишем значения переменных в ходе цикла, пока не выполнится следующее условие «а<9» .

Шаг 1.	Проверяем условие «а<b», условия не выполняется (идем по стрелки «нет»). b=b2=12=2 a=a+2=1+2=3
Шаг 2.	Проверяем условие «а<b», условия не выполняется (идем по стрелки «нет»). b=b2=22=4 a=a+2=3+2=5
Шаг 3.	Проверяем условие «а<b», условия не выполняется (идем по стрелки «нет»). b=b2=42=8 a=a+2=5+2=7
Шаг 4.	Проверяем условие «а<b», условия выполняется (идем по стрелки «да»). b=b+2=8+2=10 a=a+2=7+2=9

Так как после четвертого шага переменная а равна 9, то по условию «а<9» , цикл завершён.
Ответ: Переменная b равна 10.

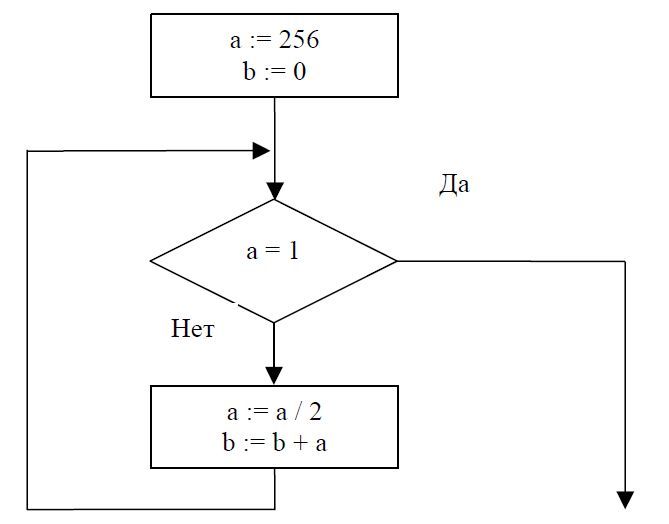
Задача №5 Определите значение переменной b после выполнения фрагмента алгоритма:

Решение задачи №5 Последовательно выпишем значения переменных в ходе цикла, пока не выполнится следующее условие «а=1» .

Шаг 1.	a=a/2=256/2=128 b=b+a=0+128=128
Шаг 2.	a=a/2=128/2=64 b=b+a=128+64=192
Шаг 3.	a=a/2=64/2=32 b=b+a=192+32=224
Шаг 4.	a=a/2=32/2=16 b=b+a=224+16=240
Шаг 5.	a=a/2=16/2=8 b=b+a=240+8=248
Шаг 6.	a=a/2=8/2=4 b=b+a=248+4=252
Шаг 7.	a=a/2=4/2=2 b=b+a=252+2=254
Шаг 8.	a=a/2=2/2=1 b=b+a=254+1=255

Так как после восьмого шага переменная а равна 1, то по условию «а=1» , цикл завершён.
Ответ: Переменная b равна 255.

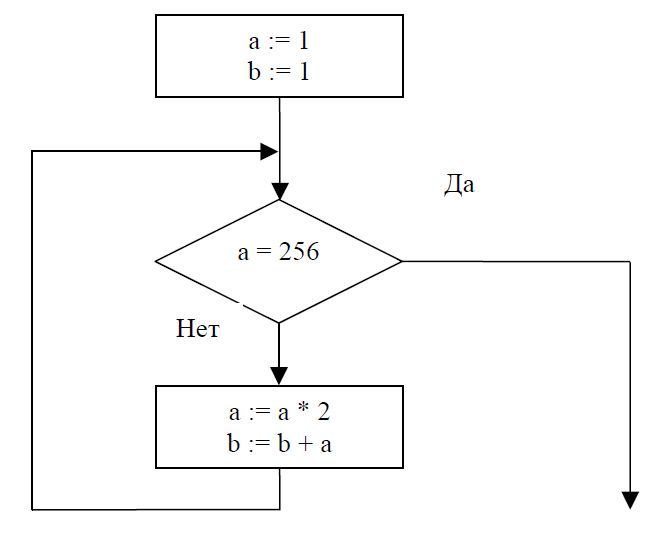
Задачи для самостоятельного решения

Задача №6 Определите значение переменной b после выполнения фрагмента алгоритма:

Задача №7 Определите значение переменной a после выполнения фрагмента алгоритма:

Анализ результата исполнения алгоритма

Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.

Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.

Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.

Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.

Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.

Основные требования, предъявляемые к алгоритмам:

Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).

Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.

Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.

Конечность: количество шагов алгоритма должно быть конечным.

Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.

Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.

Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:

следование — образуется из последовательности действий, следующих одно за другим;
ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Для описания алгоритмов наиболее распространены следующие методы (языки):

Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.

Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.

Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.

Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.

Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:

строго не формализуемы;
достаточно многословны;
могут допускать неоднозначность толкования отдельных предписаний;
сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.

Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.

Название символа	Графическое изображение	Комментарии
Пуск/Останов (блоки начала и конца алгоритма)		Указание на начало или конец алгоритма
Ввод/Вывод данных (блоки ввода, вывода		Организация ввода/вывода в общем виде
Процесс (операторные блоки)		Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных
Условие (условный блок)		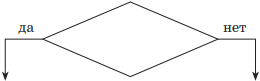Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия
Начало цикла с параметром		Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков
Предопределенный процесс		Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам
Печать сообщений (документ)		Вывод результатов на печать

При составлении блок-схемы необходимо проверять выполнение следующих условий:

из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.

Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:

алг — заголовок алгоритма	нц — начало цикла	знач
нач — начало алгоритма	кц — конец цикла	и
кон — конец алгоритма	дано	или
арг — аргумент	надо	не
рез — результат	если	да
цел — целый	то	нет
сим — символьный	иначе	при
лит — литерный	всё	выбор
лог — логический	пока	утв
вещ — вещественный	для	ввод
таб — таблица	от	вывод
длин — длина	до

Общий вид записи алгоритма на псевдокоде:

алг — название алгоритма (аргументы и результаты)

дано — условие применимости алгоритма

надо — цель выполнения алгоритма

нач — описание промежуточных величин

последовательность команд (тело алгоритма)

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.

Команды учебного языка:

1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.

2. Операторы ввода/вывода:

ввод (список имен переменных)

вывод (список вывода)

Список вывода может содержать комментарии, которые заключаются в кавычки.

3. Оператор ветвления (с использованием команды если. то… иначе…всё; выбор);

4. Операторы цикла (с использованием команд для, пока, до).

Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.

Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:

первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).

Примеры решения задач

Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:

Первая команда уменьшает число на 1, вторая — увеличивает его втрое.

Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.

Ответ: 13311

Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.

Система команд Исполнителя алгоритма:

1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).

2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?

1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.

2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).

3. Все эти команды можно заменить одной — «Назад 5».

Ответ: команда«Назад 5».

Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:

Название команды	Параметр	Действия исполнителя
вп	Число шагов	Продвигается в направлении головы на указанное число шагов
нд	Число шагов	Продвигается в направлении, противоположном направлению головы на указанное число шагов
пр	Число градусов	Поворачивается направо относительно направления, заданного головой черепашки
лв	Число градусов	Поворачивается налево относительно направления, заданного головой черепашки

Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.

Записать для исполнителя Черепашка алгоритмы:

а) построения квадрата со стороной 100;

б) построения правильного шестиугольника со стороной 50.

в) построения изображения цифры 4, если голова Черепашки смотрит на север.

Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].

Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.

Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.

1-й ход	2-й ход
Начало	1-й игрок	2-й игрок	1-й игрок	2-й игрок
2,3,4	4,3,4	8,3,4	выигрыш
4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
4,3,8	выигрыш
6,5,6	12,5,6	выигрыш
6,10,6	выигрыш
6,5,12	выигрыш
8,7,8	выигрыш
2,6,4	4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
2,12,4	выигрыш
2,6,8	выигрыш
4,8,6	выигрыш
2,3,8	выигрыш
4,5,6	8,5,6	выигрыш
4,10,6	выигрыш
4,5,12	выигрыш
6,7,8	выигрыш

Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):

Какой символ находится в последней строке на 250-м месте (считая слева направо)?

Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.

Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:

(6) 127*2+1=255 символов.

Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.

Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:

n := Длина(а)

b := Извлечь(а, k)

нц для i от 7 до n – 1

с := Извлечь(а, i)

b := Склеить(b, с)

Здесь переменные а, b, с — строкового типа; переменные n, i — целые.

В алгоритме используются следующие функции:

Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».

Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.

Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.

Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?

Решение. Находим общее число символов в строке а, получим, что n = 11.

Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.

В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.

В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).

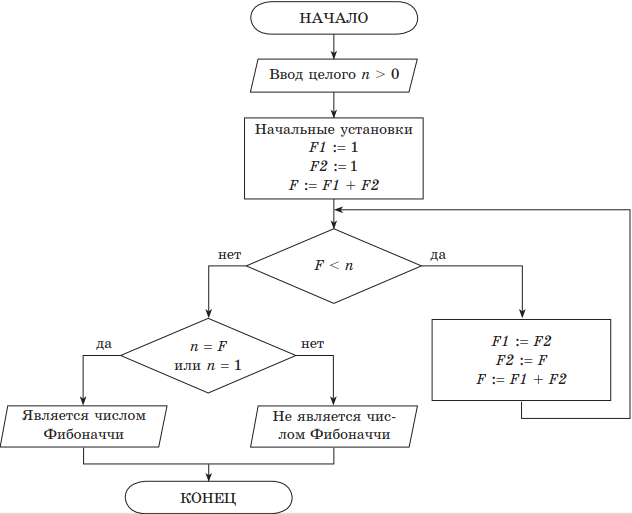
Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.

В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.

Решение. Словесный алгоритм:

Ввести число n.
Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.

Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.

F — текущее число ряда Фибоначчи;

F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;

n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.

Учебный алгоритмический язык	Язык блок-схем
действие 1 действие 2 … действие n

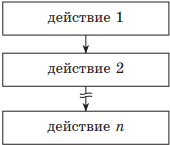Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.

В качестве примера рассмотрим решение простой задачи.

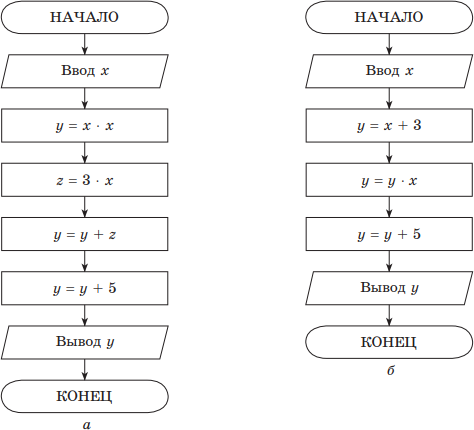
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.

Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.

Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).

Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.

Обратите внимание, как в блоке следования используется оператор присваивания.

Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.

В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.

Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.

Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).

Как определить значение переменной после выполнения алгоритма

Задания Д7 № 369

В алгоритме, записанном ниже, используются переменные a и b. Символ «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной a после выполнения алгоритма:

В ответе укажите одно целое число — значение переменной a.

b := 100 + a/b = 102

a := b/6*a = 17 · 10 = 170.

Задания Д7 № 389

Источник

Основные алгоритмические конструкции

Алгоритм применительно к вычислительной машине — точное предписание, т.е. набор операций и правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа.

Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

Линейный алгоритм — набор команд (указаний), выполняемых последовательно друг за другом.

Основным элементарным действием в линейных алгоритмах является присваивание значения переменной величине. Если значение константы определено видом ее записи, то переменная величина получает конкретное значение только в результате присваивания. Присваивание может осуществляться двумя способами: с помощью команды присваивания и с помощью команды ввода.

Рассмотрим пример. В школьном учебнике математики правила деления обыкновенных дробей описаны так:

Числитель первой дроби умножить на знаменатель второй дроби.
Знаменатель первой дроби умножить на числитель второй дроби.
Записать дробь, числитель которой есть результат выполнения пункта 1, а знаменатель — результат выполнения пункта 2.

В алгебраической форме это выглядит следующим образом:

Построим алгоритм деления дробей для ЭВМ. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, Ь, с, d. Результатом — также целые величины m и n. Блок-схема и текст алгоритма на языке программирования (ЯП) Kotlin приведены ниже.

namespace oap
{
    class Program
    {
        static void Main(string[] args)
        {
            Console.WriteLine("Enter a, b, c, d: ");
            var a = int.Parse(Console.ReadLine());
            var b = int.Parse(Console.ReadLine());
            var c = int.Parse(Console.ReadLine());
            var d = int.Parse(Console.ReadLine());
            var m = a * d;
            var n = b * c;
            Console.WriteLine($"m={m}, n={n}");
        }
    }
}

Формат команды присваивания следующий:

Знак «=» нужно читать как «присвоить».

Команда присваивания обозначает следующие действия, выполняемые компьютером:

Вычисляется выражение.
Полученное значение присваивается переменной.

В приведенном выше алгоритме присутствуют две команды присваивания. В блок-схемах команда присваивания записывается в прямоугольнике. Такой блок называется вычислительным блоком.

В описаниях алгоритмов необязательно соблюдать строгие правила в записи выражений. Их можно писать в обычной математической форме. Это еще не язык программирования со строгим синтаксисом.

В приведенном алгоритме присутствуют команды ввода:

var a = int.Parse(Console.ReadLine());
var b = int.Parse(Console.ReadLine());
var c = int.Parse(Console.ReadLine());
var d = int.Parse(Console.ReadLine());

В блок-схеме команда ввода записывается в параллелограмме — блоке ввода-вывода. При выполнении данной команды процессор прерывает работу и ожидает действий пользователя. Пользователь должен набрать на устройстве ввода (клавиатуре) значения вводимых переменных и нажать на клавишу ввода Enter. Обычно с помощью команды ввода присваиваются значения исходных данных, а команда присваивания используется для получения промежуточных и конечных величин.

Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для этих целей предназначена команда вывода:

Console.WriteLine($"m={m}, n={n}");

С помощью этой команды результаты выводятся на экран или на устройство печати на бумагу.

Поскольку присваивание является важнейшей операцией в вычислительных алгоритмах, обсудим ее более подробно.

Рассмотрим последовательное выполнение четырех команд присваивания, в которых участвуют две переменные величины a и b.

В приведенной ниже таблице напротив каждой команды присваивания указываются значения переменных, которые устанавливаются после ее выполнения.

Команда	a	b
a=1	1	—
b=a*2	1	2
a=b	2	2
b=a+b	2	4

Этот пример иллюстрирует три основных свойства команды присваивания:

пока переменной не присвоено значение, она остается неопределенной;
значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующей команды присваивания этой переменной;
новое значение, присваиваемое переменной, заменяет ее предыдущее значение.

Рассмотрим один очень полезный алгоритм, который приходится часто использовать при программировании. Даны две величины: Х и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было Х=1, Y=2, то после обмена должно стать: Х=2, Y=1.

Хорошей моделью для решения этой задачи является следующая ситуация: имеются два стакана — один с молоком, другой с водой. Требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: 1) перелить из первого стакана в третий; 2) перелить из второго в первый;
3) перелить из третьего во второй. Цель достигнута!

По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача обмена решается последовательным выполнением трех команд присваивания:

Команда	X	Y	Z
ввод X, Y	1	2	—
Z = X	1	2	1
X = Y	2	2	1
Y = Z	2	1	1

Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х = Y) переменная, стоящая справа (Y), сохраняет свое значение.

Алгоритм для деления дробей имеет линейную структуру. В нем все команды выполняются в строго однозначной последовательности, каждая по одному разу. Линейный алгоритм составляется из команд присваивания, ввода, вывода и обращения к вспомогательным алгоритмам (об этом позже).

При описании алгоритмов в блок-схемах типы, как правило, не указываются (но подразумеваются). В алгоритмах для всех переменных типы указываются явно. В них используются следующие обозначения типов: Int — целый тип, Float — вещественный тип, String — символьный (литерный) тип, Boolean — логический тип. В алгоритме для деления дробей для всех переменных указан тип Int.

Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.

Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторому условию.

Составим алгоритм решения квадратного уравнения: ax²+bx+c=0

Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня х1 и х2, которые вычисляются по формуле:

namespace oap
{
    class Program
    {
        static void Main(string[] args)
        {
            Console.WriteLine("Введите a, b, c: ");
            var a = int.Parse(Console.ReadLine());
            var b = int.Parse(Console.ReadLine());
            var c = int.Parse(Console.ReadLine());
            var d = b * b - 4 * a * c;
            var x1 = (-b + Math.Sqrt(d)) / (2 * a);
            var x2 = (-b - Math.Sqrt(d)) / (2 * a);
            Console.WriteLine($"x1={x1}, x2={x2}");
        }
    }
}

Введите a, b, c:
3
2
1
x1=NaN, x2=NaN

Слабость такого алгоритма видна невооруженным глазом. Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам, — универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).

Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.

Решение уравнения зависит от значений коэффициентов а, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней):

если а = 0, b = 0, с = 0, то любое х — решение уравнения;
если а = 0, b = 0, с <> О, то уравнение действительных решений не имеет;
если а = 0, b <> О, то это линейное уравнение, которое имеет одно решение х = -c/b;
если а<>0 и d=b²-4ac >= 0, то уравнение имеет два вещественных корня (формулы приведены выше);
если a<>0 и d<0, то уравнение не имеет вещественных корней.

Этот же алгоритм на Kotlin:

fun main(){
    println("Введите a, b, c:")
    val a = readLine()!!.toInt()
    val b = readLine()!!.toInt()
    val c = readLine()!!.toInt()

    var x1: Float

    if(a==0){
        if(b==0){
            if(c==0) println("любое X")
            else println("нет решений")
        } else {
            x1 = -c.toFloat()/b
            println("X=$x1")
        }
    } else {
        val d = b*b-4*a*c
        if(d<0) println("нет вещественных корней")
        else{
            x1 = (-b+sqrt(d.toFloat()))/(2*a)
            val x2 = (-b-sqrt(d.toFloat()))/(2*a)
            println("x1=$x1, x2=$x2")
        }
    }
}

В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на ЯП следующий:

if (условие) {серия1}
else {серия2}

Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется серия 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется серия 2 (отрицательная ветвь). В языке Kotlin условие записывается после служебного слова if, положительная ветвь — сразу после условия, отрицательная — после слова else.

Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «Корни квадратного уравнения».

Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала:

Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая п = 3.

Шаг	n	F	i	Условие
1	3
2		1
3			1
4				1<=3, да
5		1
6			2
7				2<=3, да
8		2
9			3
10				3<=3, да
11		6
12			4
13				4<=3, нет
14		вывод

Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на ЯП.

fun main(){
    println("Введите n:")
    val n = readLine()!!.toInt()
    var F = 1
    var i = 1
    while (i<=n){
        F *= i  // F = F*i
        i++     // i = i+1
    }
    println("F=$F")
}

Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда цикл-пока, или цикл с предусловием. Общий вид команды цикл-пока в блок-схемах и в ЯП следующий:

while (условие) {
  //серия
}

Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение.

Цикл с предусловием — это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции:

если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля — еще один признак хорошего качества программы.

fun main(){
    var a: Int
    do {
        println("Введите a:")
        a = readLine()!!.toInt()
    } while(a!=0)

    val d = b*b-4*a*c
    if(d<0) println("нет вещественных корней")
    else{
        val x1 = (-b+sqrt(d.toFloat()))/(2*a)
        val x2 = (-b-sqrt(d.toFloat()))/(2*a)
        println("x1=$x1, x2=$x2")
    }
}

В общем виде структурная команда цикл с постусловием или цикл — до представляется так:

do {
  //серия
} while (условие)

Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.

Составим алгоритм решения следующей задачи: даны два натуральных числа М и N. Требуется вычислить их наибольший общий делитель — НОД(M, N).

Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(М, N) = НОД(М-N,N). Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, М) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции:

Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма
Определить большее из чисел
Заменить большее число разностью большего и меньшего значений
Вернуться к выполнению пункта 1

fun main(){
    println("Введите m, n: ")
    var m = readLine()!!.toInt()
    var n = readLine()!!.toInt()
    while (m!=n){
        if(m>n) m = m-n
        else n = n-m
    }
    println("НОД = $m")
}

Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая М = 18, N = 12. В результате получится НОД = 6, что, очевидно, верно.

Вспомогательные алгоритмы и процедуры

В теории алгоритмов известно понятие вспомогательного алгоритма. Вспомогательным называется алгоритм решения некоторой подзадачи из основной решаемой задачи. В таком случае алгоритм решения исходной задачи называется основным алгоритмом.

В качестве примера рассмотрим следующую задачу: требуется составить алгоритм вычисления степенной функции с целым показателем у = х^к, где к — целое число, х<>0. В алгебре такая функция определена следующим образом:

Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень.

Учитывая, что 1/х^-n = (1/х)^-n, запишем основной алгоритм решения этой задачи.

fun main(){
    println("Введите x, n: ")
    var x = readLine()!!.toFloat()
    var n = readLine()!!.toInt()
    var y: Float

    if(n==0) y = 1F
    else {
        if(n>0) y = stepen(x, n)
        else y = stepen(1/x, -n)
    }
   
    println("y = $y")
}

Здесь дважды присутствует команда обращения к вспомогательному алгоритму с именем stepen. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами.

В котлине вспомогательные алгоритмы оформляются в виде функций. Запишем функцию stepen.

fun stepen(x: Float, n: Int): Float {
    var res = 1F
    var i = 1
    while(i<=n){
        res = res * x
        i++
    }
    return res
}

Заголовок вспомогательного алгоритма начинается с ключевого слова fun, после которого следует имя функции, в скобках — список формальных параметров и после скобок тип результата (не обязателен). В списке параметров перечисляются переменные-аргументы с указанием их типов. Здесь x и n — формальные параметры-аргументы. Следовательно, процедура stepen производит вычисления по формуле а^к. В основном алгоритме «Степенная функция» обращение к процедуре производится путем указания ее имени с последующим в скобках списком фактических параметров. Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия:

по количеству (сколько формальных, столько и фактических параметров)
по последовательности (первому формальному соответствует первый фактический параметр, второму — второй и т.д.)
по типам (типы соответствующих формальных и фактических параметров должны совпадать)

Фактические параметры-аргументы могут быть выражениями соответствующего типа.

Обращение к процедуре инициирует следующие действия:

Значения параметров-аргументов присваиваются соответствующим формальным параметрам.
Выполняется тело процедуры (команды внутри процедуры).
Значение результата возвращается командой return, и происходит переход к выполнению следующей команды основного алгоритма.

В функции stepen нет команд ввода исходных данных и вывода результатов. Здесь присваивание начальных значений аргументам (x, n) производится через передачу параметров-аргументов. А получение результата происходит командой return. Таким образом, передача значений параметров процедур — это третий способ присваивания (наряду с командой присваивания и командой ввода).

Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации.

Программы для графического отображения алгоритмов

https://draw.io (онлайн)
Microsoft Visio
Dia (бесплатная)

КОНТРОЛЬНЫЕ ВОПРОСЫ

Линейный алгоритм
Разветвляющийся алгоритм
Циклический алгоритм
Вспомогательные алгоритмы и процедуры

Источник

Практическая
раборта № 1

Построение
блок-схем алгоритмов(теория)

Предпочтительнее
до записи на алгоритмическом языке представить алгоритм в виде блок-схемы. Для
построения алгоритма в виде блок-схемы необходимо знать назначении каждого из
блоков. В таблице 1. приводятся типы блоков и их назначение.

Таблица 1

№	Блок	Назначение блока
1		Начало или конец блок-схемы
2		Ввод или вывод данных
3		Процесс (в частности вычислительный)
4		условие
6		Цикл с параметром (for)

Основные
типы алгоритмов

Алгоритмизация выступает как набор
определенных практических приёмов, особых специфических навыков рационального
мышления в рамках заданных языковых средств. Алгоритмизация вычислений
предполагает решение задачи в виде последовательности действий, т.е. решение,
представленное в виде блок-схемы. Можно выделить типичные алгоритмы. К ним
относятся: линейные алгоритмы, разветвляющиеся алгоритмы, циклические
алгоритмы.

Линейные алгоритмы

Линейный алгоритм является наиболее
простым. В нём предполагается последовательное выполнение операций. В этом
алгоритме не предусмотрены проверки условий или повторений.

Пример: Вычислить функцию z=
(х-у)/x +y².

Составить блок-схему вычисления функции по
линейному алгоритму. Значения переменных х, у могут быть
любые, кроме нуля, вводить их с клавиатуры.

Решение: Линейный алгоритм вычисления
функции задан в виде блок-схемы на рис.1. При выполнении линейного алгоритма
значения переменных вводятся с клавиатуры, подставляются в заданную функцию,
вычисляется результат, а затем выводится результат.

Рис.1. Линейный алгоритм

Назначение блоков в схеме на
рис.1:

·
Блок 1 в схеме служит в качестве
логического начала.

·
Блок 2 соответствует вводу данных.

·
Блок 3 представляет арифметическое
действие.

·
Блок 4 выводит результат.

·
Блок 5 в схеме служит в качестве
логического завершения схемы.

Алгоритмы ветвлений

Разветвляющийся алгоритм предполагает
проверку условий для выбора решения. Соответственно в алгоритме появятся две
ветви для каждого условия.

В
примере рассматривается разветвляющийся алгоритм, где в зависимости от условия
выбирается один из возможных вариантов решений. Алгоритм представляется в виде
блок-схемы.

Пример:
При выполнении условия x>0
вычисляется функция: z=
x+
y,
иначе, а именно, когда х=0 или x<0,
вычисляется функция: z=x²+y².

Составить
блок-схему вычисления функции по алгоритму ветвления. Значения переменных х,
у могут быть любые, вводить их с клавиатуры.

Решение:
На рис.2 представлен разветвляющийся алгоритм, где в зависимости от условия
выполнится одна из веток. В блок-схеме появился новый блок 3, который проверяет
условие задачи. Остальные блоки знакомы из линейного алгоритма.

Рис.2. Алгоритм ветвления

Пример: Найти максимальное значение
из трёх различных целых чисел, введенных с клавиатуры. Составить блок-схему
решения задачи.

Решение: Данный алгоритм
предполагает проверку условия. Для этого выбирается любая из трёх переменных и
сравнивается с другими двумя. Если она больше, то поиск максимального числа
окончен. Если условие не выполняется, то сравниваются две оставшиеся
переменные. Одна из них будет максимальной. Блок-схема к этой задаче
представлена на рис 3.

Рис. 3. Блок-схема поиска максимума

Циклические алгоритмы

Циклический алгоритм предусматривает
повторение одной операции или нескольких операций в зависимости от условия
задачи.

Из
циклических алгоритмов выделяют два типа:

1)
с заданным количеством циклов или со
счётчиком циклов;

2)
количество циклов неизвестно.

Пример:
В цикле вычислить значение функции z=x*y при условии, что одна из
переменных x
меняется в каждом цикле на единицу, а другая переменная у не
меняется и может быть любым целым числом. В результате выполнения цикла при
начальном значении переменной х=1 можно получить таблицу умножения.
Количество циклов может быть любым. Составить блок-схему решения задачи.

Решение:
В примере количество циклов задаётся. Соответственно выбирается алгоритм
циклов первого типа. Алгоритм этой задачи приводится на рис. 4.

Во
втором блоке вводятся количество циклов n и любые целые числа х,
y.

В
блок-схеме появился новый блок 3, в котором переменная i считает
количество циклов, после каждого цикла увеличиваясь на единицу, пока счётчик не
будет равен i=n. При i=n будет выполнен последний
цикл.

В
третьем блоке указывается диапазон изменения счётчика цикла (от i =1 до i=n).

В
четвёртом блоке изменяются значения переменных: z, x.

В
пятом блоке выводится результат. Четвёртый и пятый блоки повторяются в каждом
цикле.

Рис.4 . Циклический алгоритм со счётчиком
циклов

Этот
тип циклических алгоритмов предпочтителен, если дано количеством циклов.

Если количество циклов неизвестно, то
блок-схемы циклических алгоритмов могут быть представлены в виде рисунков 5, 6.

Пример:
Вычислить у=у-x
пока y>x,
если y=30,
x=4.
Подсчитать количество выполненных циклов, конечное значение переменной у.
В цикле вывести значение переменной у, количество выполненных
циклов. Составить блок-схему решения задачи.

Решение:
В примере количество циклов неизвестно. Соответственно выбирается алгоритм
циклов второго типа. Алгоритм этой задачи приводится на рис. 5.

Условие
проверяется на входе в цикл. В теле цикла выполняется два блока:

1)
у=у-х; i=i+1;

2)
вывод значений переменных i,
y.

Цикл
выполняется до тех пор, пока выполняется условие y>x. При условии
равенства этих переменных у=х или y<x цикл заканчивается.

Алгоритм,
представленный на рис.5, называется циклический алгоритм с предусловием,
так как условие проверяется в начале цикла или на входе в цикл.

Рис.5. Блок-схема
циклического алгоритма с предусловием

Во втором блоке вводятся y=30,
x=4.

В
третьем блоке проверяется условие y>x
на входе в цикл. Если условие выполняется, то переход к блоку 4, иначе на блок
6.

В
четвёртом блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.

В
пятом блоке выводится результат:

·
значение переменной у,

·
количество выполненных циклов i.

Пример:
Составить блок-схему примера (рисунок 5), проверяя условие выхода из цикла.
В этом примере условие задачи не меняется, и результат выведется тот же, но
блок-схема будет другой.

Решение:
В этом случае проверяется условие на выход из цикла: y<=x. При
этом условии цикл не выполняется. Условие в блок-схеме следует перенести в
конец цикла, после вывода на печать. Цикл выполняется до тех пор, пока
выполняется условие y>x.

Алгоритм,
если условие перенести в конец цикла, называется алгоритмом цикла с
постусловием. Алгоритм этой задачи приводится на рис. 6.

Во
втором блоке вводятся y=30,
x=4.

В
третьем блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.

В
четвёртом блоке выводится результат:

·
значение переменной у,

·
количество выполненных циклов i.

В
пятом блоке проверяется условие y<=x
на выход из цикла. Если условие выполняется, то переход к блоку 6, иначе на
блок 3 и цикл повторяется.

Рис.6 . Алгоритм цикла с
постусловием

Индивидуальные задания к работе:

1.
Найти
результат работы алгоритма:

Входные данные по вариантам

№	A	B	C	D
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0
5	4	3	2	1
6	5	4	3	2
7	6	5	4	3
8	7	6	5	4
9	-3	7	6	5
10	-4	-3	7	6
11	-5	-4	-3	7
12	-6	-5	-4	-3
13	-7	-6	-5	-4
14	9	-7	-6	-5
15	8	7	-7	-6
16	5	5	8	-7
17	5	2	4	5

2. При
заданном Х условие выполнется? Написать результат вычисления и ответ попадаем в
условие или нет.

Входные данные по вариантам

№	X1	X1
1	55	12
2	85	13
3	24	17
4	65	15
5	17	54
6	15	67
7	26	3
8	27	21
9	92	34
10	12	23
11	45	22
12	66	45
13	71	46
14	13	76
15	45	67
16	53	35
17	52	23

3. Написать
результат выполнения алгоритма с указанными входными данными

Входные данные по вариантам

№	S
1	1,5
2	1,8
3	2,4
4	1,6
5	1,7
6	1,3
7	2,6
8	2,37
9	1,92
10	1,12
11	1,45
12	2,66
13	2,71
14	2,13
15	1,45
16	2,53
17	1,52

4. Написать
результат выполнения алгоритма с указанными входными данными

Входные данные по вариантам

№	X
1	-1
2	0
3	1
4	2
5	3
6	4
7	5
8	6
9	7
10	-3
11	-4
12	-5
13	-6
14	-7
15	7
16	5
17	2

5. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

6. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Дано двузначное число. Найти: число десятков в нем;
2	Дано двузначное число. Найти: число единиц в нем;
3	Дано двузначное число. Найти: сумму его цифр;
4	Дано двузначное число. Найти: произведение его цифр.
5	Дано двузначное число. Получить число, образованное при перестановке цифр заданного числа.
6	Дано трехзначное число. Найти: ачисло единиц в нем;
7	Дано трехзначное число. Найти: число десятков в нем;
8	Дано трехзначное число. Найти: сумму его цифр;
9	Дано трехзначное число. Найти: произведение его цифр.
10	Дано трехзначное число. Найти число, полученное при прочтении его цифр справа налево.
11	Дано трехзначное число. В нем зачеркнули первую слева цифру и приписали ее в конце. Найти полученное число.
12	Дано трехзначное число. В нем зачеркнули последнюю справа цифру и при- писали ее в начале. Найти полученное число.
13	Дано трехзначное число. Найти число, полученное при перестановке первой и второй цифр заданного числа
14	Дано трехзначное число. Найти число, полученное при перестановке второй и третьей цифр заданного числа.
15	Дано трехзначное число, в котором все цифры различны. Получить шесть чи- сел, образованных при перестановке цифр заданного числа.
16	Дано натуральное число n (n > 9). Найти: число единиц в нем;
17	Дано натуральное число n (n > 9). Найти: число десятков в нем.

7. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Определить максимальное и минимальное значения из двух различных веще- ственных чисел.
2	Известны два расстояния: одно в километрах, другое — в футах ( 1 фут 0,305 м ). Какое из расстояний меньше?
3	Известны две скорости: одна в километрах в час, другая — в метрах в секун- ду. Какая из скоростей больше?
4	Даны радиус круга и сторона квадрата. У какой фигуры площадь больше?
5	Даны объемы и массы двух тел из разных материалов. Материал какого из тел имеет большую плотность?
6	Известны сопротивления двух несоединенных друг с другом участков элек- трической цепи и напряжение на каждом из них. По какому участку протекает меньший ток?
7	Даны вещественные числа a, b, c (a 0). Выяснить, имеет ли квадратное уравнение с данными параметрами решение
8	Известны площади круга и квадрата. Определить: уместится ли круг в квадрате?
9	Известны площади круга и квадрата. Определить: уместится ли квадрат в круге?
10	Известны площади круга и равностороннего треугольника. Определить: уместится ли круг в треугольнике?
11	Известны площади круга и равностороннего треугольника. Определить: уместится ли треугольник в круге?
12	Дано двузначное число. Определить: какая из его цифр больше: первая или вторая;
13	Дано двузначное число. Определить: одинаковы ли его цифры
14	Дано двузначное число. Определить: кратна ли трем сумма его цифр;
15	Дано двузначное число. Определить: кратна ли сумма его цифр числу а.
16	Дано трехзначное число. Определить, какая из его цифр больше: первая или последняя;
17	Дано трехзначное число. Определить, какая из его цифр больше: вторая или последняя.

8. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Одна штука некоторого товара стоит 20,4 руб. Напечатать таблицу стоимости 2, 3, …, 20 штук этого товара.
2	Напечатать таблицу соответствия между весом в фунтах и весом в килограм- мах для значений 1, 2, …, 10 фунтов (1 фунт = 453 г).
3	Напечатать таблицу перевода расстояний в дюймах в сантиметры для значе- ний 10, 11, …, 22 дюйма (1 дюйм = 25,4 мм).
4	Напечатать таблицу перевода 1, 2, … 20 долларов США в рубли по текущему курсу (значение курса вводится с клавиатуры).
5	Считая, что Земля — идеальная сфера с радиусом R 6350 км, определить расстояние до линии горизонта от точки с высотой над Землей, равной 1, 2, … 10 км.
6	. Напечатать таблицу умножения на 7:
7	Напечатать таблицу умножения на 9:
8	Напечатать «столбиком» значения sin 2 , sin 3 , …, sin 20 .
9	Напечатать таблицу стоимости 50, 100, 150, …, 1000 г сыра (стоимость 1 кг сыра вводится с клавиатуры).
10	Вывести «столбиком» следующие числа: 2,1, 2,2, 2,3, …, 2,8.
11	. Вывести «столбиком» следующие числа: 3,2, 3,2, 3,3, …, 3,9.
12	Вывести «столбиком» следующие числа: 2,2, 2,4, 2,6, …, 4,2.
13	Вывести «столбиком» следующие числа: 4,4, 4,6, 4,8, …, 6,4.
14	Напечатать таблицу стоимости 100, 200, 300, …, 2000 г конфет (стоимость 1 кг конфет вводится с клавиатуры).
15	Составить программу вывода любого числа любое заданное число раз в виде, аналогичном показанному в предыдущей задаче.
16	Напечатать таблицу умножения на 2:
17	Напечатать таблицу умножения на 5:

9. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Даны числа а1, а2, а3…а10, . Определить их сумму
2	Известна масса каждого из 12 предметов. Определить общую массу всего на- бора предметов.
3	. Известны оценки абитуриента на четырех экзаменах. Определить сумму на- бранных им баллов.
4	В ведомости указана зарплата, выплаченная каждому из сотрудников фирмы за месяц. Определить общую сумму выплаченных по ведомости денег
5	Известна масса каждого предмета, загружаемого в автомобиль. Определить общую массу груза.
6	Известно сопротивление каждого из элементов электрической цепи. Все эле- менты соединены последовательно. Определить общее сопротивление цепи.
7	Известно сопротивление каждого из элементов электрической цепи. Все эле- менты соединены параллельно. Определить общее сопротивление цепи.
8	Известны оценки по физике каждого из 20 учеников класса. Определить сред- нюю оценку.
9	Известны оценки ученика по 10 предметам. Определить среднюю оценку
10	Известны оценки по алгебре каждого ученика класса. Определить среднюю оценку
11	Известна масса каждого предмета из некоторого набора предметов. Опреде- лить среднюю массу
12	Известны оценки двух учеников по четырем предметам. Определить сумму оценок каждого ученика.
13	Известны результаты двух спортсменов-пятиборцев в каждом из пяти видов спорта в баллах. Определить сумму баллов, полученных каждым спортсменом.
14	Известен возраст (в годах в виде 14,5 лет и т. п.) каждого ученика двух клас- сов. Определить средний возраст учеников каждого класса. В каждом классе учатся 20 человек.
15	Известно количество осадков, выпавших за каждый день января и марта. Оп- ределить среднедневное количество осадков за каждый месяц
16	Известен рост каждого ученика двух классов. Определить средний рост уче- ников каждого класса. Численность обоих классов одинаковая.
17	Известны оценки по физике каждого ученика двух классов. Определить среднюю оценку в каждом классе. Количество учащихся в каждом классе одинаковое.

10. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Дано натуральное число. а) Верно ли, что сумма его цифр больше 10?
2	Дано натуральное число. б) Верно ли, что произведение его цифр меньше 50?
3	Дано натуральное число. в) Верно ли, что количество его цифр есть четное число?
4	Дано натуральное число. г) Верно ли, что это число четырехзначное? Составное условие и вложенный условный оператор не использовать.
5	Дано натуральное число д) Верно ли, что его первая цифра не превышает 6?
6	Дано натуральное число. е) Верно ли, что оно начинается и заканчивается одной и той же цифрой?
7	Дано натуральное число. ж) Определить, какая из его цифр больше: первая или последняя.
8	Дано натуральное число. а) Верно ли, что сумма его цифр меньше a?
9	Дано натуральное число. б) Верно ли, что произведение его цифр больше b?
10	Дано натуральное число. в) Верно ли, что это число k-значное? Составное условие и вложенный услов- ный оператор не использовать.
11	Дано натуральное число. г) Верно ли, что его первая цифра превышает m?
12	Дано натуральное число. а) Верно ли, что сумма его цифр больше k, а само число четное?
13	Дано натуральное число. б) Верно ли, что количество его цифр есть четное число, а само число не пре- вышает b?
14	Дано натуральное число. в) Верно ли, что оно начинается цифрой x и заканчивается цифрой y?
15	Дано натуральное число. г) Верно ли, что произведение его цифр меньше a, а само число делится на b?
16	Дано натуральное число. д) Верно ли, что сумма его цифр больше m, а само число делится на n?
17	Дано натуральное число. Определить: а) есть ли в нем цифра 3;

Источник

№	A	B	C	D
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0
5	4	3	2	1
6	5	4	3	2
7	6	5	4	3
8	7	6	5	4
9	-3	7	6	5
10	-4	-3	7	6
11	-5	-4	-3	7
12	-6	-5	-4	-3
13	-7	-6	-5	-4
14	9	-7	-6	-5
15	8	7	-7	-6
16	5	5	8	-7
17	5	2	4	5

№	X1	X1
1	55	12
2	85	13
3	24	17
4	65	15
5	17	54
6	15	67
7	26	3
8	27	21
9	92	34
10	12	23
11	45	22
12	66	45
13	71	46
14	13	76
15	45	67
16	53	35
17	52	23

№	A	B	C	D
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0
5	4	3	2	1
6	5	4	3	2
7	6	5	4	3
8	7	6	5	4
9	-3	7	6	5
10	-4	-3	7	6
11	-5	-4	-3	7
12	-6	-5	-4	-3
13	-7	-6	-5	-4
14	9	-7	-6	-5
15	8	7	-7	-6
16	5	5	8	-7
17	5	2	4	5

№	X1	X1
1	55	12
2	85	13
3	24	17
4	65	15
5	17	54
6	15	67
7	26	3
8	27	21
9	92	34
10	12	23
11	45	22
12	66	45
13	71	46
14	13	76
15	45	67
16	53	35
17	52	23

Главные элементы блок-схем алгоритмов

Задача и блок-схема алгоритма

Решение алгоритма сортировки пузырьком

2.4.1. Следование. Основные алгоритмические конструкции

2.4.2. Ветвление. Основные алгоритмические конструкции

Повторение. Основные алгоритмические конструкции

Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием)

Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром)

Основные алгоритмические конструкции. Самое главное

Основные алгоритмические конструкции. Вопросы и задания

Решение задач на выполнение алгоритма

Анализ результата исполнения алгоритма

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Как определить значение переменной после выполнения алгоритма

Основные алгоритмические конструкции

Вспомогательные алгоритмы и процедуры

Программы для графического отображения алгоритмов

Основные типы алгоритмов

Основные
типы алгоритмов

№	A	B	C	D
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0
5	4	3	2	1
6	5	4	3	2
7	6	5	4	3
8	7	6	5	4
9	-3	7	6	5
10	-4	-3	7	6
11	-5	-4	-3	7
12	-6	-5	-4	-3
13	-7	-6	-5	-4
14	9	-7	-6	-5
15	8	7	-7	-6
16	5	5	8	-7
17	5	2	4	5

№	X1	X1
1	55	12
2	85	13
3	24	17
4	65	15
5	17	54
6	15	67
7	26	3
8	27	21
9	92	34
10	12	23
11	45	22
12	66	45
13	71	46
14	13	76
15	45	67
16	53	35
17	52	23