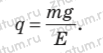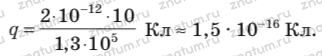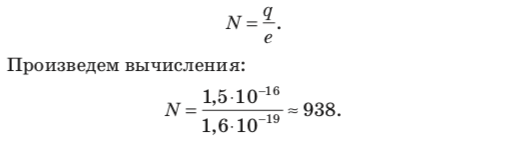Как найти чему равен заряд капли

Решение.
Сила гравитационного взаимодействия двух водяных капель определяется по формуле:

[ begin{align}
  & {{F}_{1}}=Gcdot frac{{{m}_{1}}cdot {{m}_{2}}}{{{R}^{2}}}, {{m}_{1}}={{m}_{2}}=m, {{F}_{1}}=Gcdot frac{{{m}^{2}}}{{{R}^{2}}} (1). \
 & m=rho cdot V, V=frac{1}{6}cdot pi cdot {{d}^{3}}, m=rho cdot frac{1}{6}cdot pi cdot {{d}^{3}} (2). {{F}_{1}}=frac{G}{{{R}^{2}}} cdot {{(rho cdot frac{1}{6}cdot pi cdot {{d}^{3}})}^{2}} (3). \
end{align} ]

Где: R – расстояние между центрами капель, G = 6,67∙10^-11 Н∙м²/кг², G – гравитационная постоянная, m – масса капли, V – объем капли, d – диаметр капли, ρ – плотность воды, ρ = 10³ кг/м³.
Кулоновскую силу определим по формуле:

[ {{F}_{2}}=frac{kcdot {{q}_{1}}cdot {{q}_{2}}}{{{R}^{2}}}, {{q}_{1}}={{q}_{2}}=q, {{F}_{2}}=frac{kcdot {{q}^{2}}}{{{R}^{2}}} (4). ]

k = 9∙10⁹ Н∙м² / Кл².
Сила гравитационного притяжения двух водяных одинаково заряженных капель в 100 раз меньше кулоновской силы отталкивания. Определим заряд капель.

[ begin{align}
  & 100cdot {{F}_{1}}={{F}_{2}},100cdot frac{G}{{{R}^{2}}} cdot {{(rho cdot frac{1}{6}cdot pi cdot {{d}^{3}})}^{2}}=frac{kcdot {{q}^{2}}}{{{R}^{2}}}, {{q}^{2}}=frac{100cdot G}{k} cdot {{(rho cdot frac{1}{6}cdot pi cdot {{d}^{3}})}^{2}},  \
 & q=(rho cdot frac{1}{6}cdot pi cdot {{d}^{3}})cdot 10cdot sqrt{frac{G}{k}} (5). \
 & q={{10}^{3}}cdot frac{1}{6}cdot 3,14cdot {{(0,2cdot {{10}^{-3}})}^{3}}cdot 10cdot sqrt{frac{6,67cdot {{10}^{-11}}}{9cdot {{10}^{9}}}}=3,6cdot {{10}^{-18}}. \
end{align}
 ]

Ответ: 3,6∙10^-18 Кл.

Задача: Вектор напряженности однородного электрического поля направлен вниз, напряженность этого поля равна 1,3 ∙ 10⁵ В/м. В это поле помещена капелька масла массой 2 ∙ 10^–9 г. Капелька оказалась в равновесии. Найти заряд капельки и число избыточных электронов на ней.

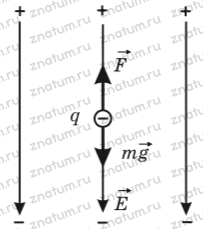
Пояснение: Обозначим Е напряженность электрического поля, m — массу капельки, g — ускорение свободного падения, F — силу, с которой электрическое поле действует на капельку, q — заряд капельки, e — модуль заряда электрона, N — число избыточных электронов на капельке.

Решение:
Поскольку капелька содержит из­ быточные электроны, ее заряд отрицателен. Положительные заряды — источники электрического поля — расположены над капелькой и притягивают ее, а расположенные под ней отрицательные заряды отталкивают капельку, поэтому сила F, с которой поле действует на капельку, направлена вверх. Ей противодействует сила тяжести mg, направленная вниз.

Капелька находится в равно­весии, значит, эти силы уравновешивают друг друга и их модули одинаковы:

F = mg.

Из определения напряженности си­ла F, действующая на капельку, рав­на: F = qE, поэтому qE = mg, откуда

Выразим в единицах СИ массу ка­ пельки: 2 ∙ 10^–9 г = 2 ∙ 10^–12 кг.

Произведем вычисления:

Число избыточных электронов найдем, разделив модуль заряда капельки, т.е. заряд всех избыточных электронов, на модуль заряда одного электрона:

Ответ: q = 1,5 ∙ 10^–16 Кл, N = 938.

Заряд — капля

Cтраница 4

Величина P / ( Ei) для данной капли является величиной постоянной. Таким образом, измерение изменения заряда капли сводится к измерению пути, пройденного каплей, и времени, за которое был пройден этот путь. Эти данные можно было надежно и точно измерять.
 [46]

Существующие процессы электроокраски различаются в первую очередь способом зарядки материала, и связанной с этим величиной заряда капли; заряд капли в свою очередь влияет на протекание всех остальных процессов электроокраски. Для улучшения процесса желательно, чтобы заряд капли был максимальным.
 [47]

Для ртутного капельного электрода этот остаточный ток известен как ток заряжения или конденсаторный ток. Это происходит от того, что, поскольку растет каждая электрически заряженная капля, необходимо постепенно увеличивать заряд капли соответственно наложенному потенциалу. С увеличением поверхности капли электроны должны течь во внешней цепи в направлении ртутного резервуара или от него, в зависимости от того, является ли поверхность ртути положительной или отрицательной стороной двойного слоя.
 [48]

Кроме геометрии самого капилляра на величину его характеристик влияют еще два фактора. Период капания t для данного электрода зависит еще и от наложенного потенциала, так как поверхностное натяжение на границе ртуть — раствор зависит от заряда капли. Обычно t достигает максимального значения около — 0 4 В ( относительно насыщенного каломельного электрода) и затем быстро уменьшается; при потенциале — 2 0 В t может составлять не больше половины максимальной величины. К счастью, в уравнение для диффузионного тока t входит в степени 1 / 6, и поэтому в небольшом интервале потенциалов уменьшение силы тока вследствие этих изменений ничтожно мало.
 [49]

Вильсон [ 167] установил, что если в обеспыленном воздухе содержатся ионы, для конденсационного образования водяных капель необходима более низкая степень пересыщения, чем в отсутствии ионов. Если на частице находится заряд, свободная энергия ее поверхности возрастает на величину ( j2 / ( l / e 0 — 1 / е), где q — заряд капли или ионного кластера, i Q и t — диэлектрические проницаемости газовой среды и жидкости соответственно, d — диаметр капли.
 [51]

Если при указанных условиях напряженность электрического поля Е равна 1 92 — 105Н / Кл, а радиус капли 1 64 — 10 — 4 см ( плотность масла равна 0 851 г / см3), чему равен заряд капли.
 [52]

Особо важное значение имеет размер капель. В зависимости от вида распыляющего устройства размер ( диаметр) капли может быть от нескольких микрон до миллиметра. Заряд капли зависит, в частности, от площади ее поверхности. В установках электростатической окраски лакокрасочный материал необходимо распылять исключительно в мелкие капли, так как крупные капли ( большого веса) не могут обладать зарядом, достаточным для направленного движения.
 [53]

Многократно повторяя измерение заряда одной и той же капли, можно заметить, что этот заряд время от времени меняется. Причиной изменения заряда капли может быть ионизация воздуха космическими лучами. Изменение заряда капли может происходить также в результате фотоэффекта при взаимодействии фотонов с веществом капли.
 [54]

В первой и второй графах записываются соответственно время опускания и время подъема капли, усредненные для ряда наблюдений за движением капли с одним и тем же зарядом. Разброс скоростей в этом случае относится к погрешностям эксперимента. В третьей графе записывается заряд капли в относительных единицах. В четвертой графе помещаются разности между двумя последующими числами третьей графы.
 [55]

При небольших количествах введенной СаО возникало расслаивание жидкости, и значение v практически не уменьшалось. Это обстоятельство указывает на повышение плотности заряда капли.
 [56]

Мицеллы воды в водно-топливных эмульсиях также не проявляют свойств дипольности. Картина резко меняется при наложении на эмульсию внешнего электрического поля, когда молекулы воды в каплях получают строгую ориентацию и капли превращаются в диполи. Одинаковая напряженность электрического поля во всех его точках, а также равенство отрицательного и положительного зарядов капли приводят к тому, что она растягивается. Это происходит до тех пор, пока силы поверхностного натяжения, стремящиеся придать капле сферическую форму, не станут равными электростатическим силам внутреннего давления, стремящимся разорвать каплю.
 [57]

Заряд — е одного электрона является наименьшим возможным электрическим зарядом — элементарным электрическим зарядом. Его можно определить также методом Милликена ( 1910), основанным на измерении силы, с которой электрическое поле известной величины действует на мельчайшую электрически заряженную каплю масла или ртути радиусом 10 — 4 — 10 — 5 см, свободно падающую в воздухе между обкладками конденсатора. За движением отдельной капли наблюдают с помощью микроскопа; по измеренной таким образом скорости можно установить заряд капли. Так было установлено, что электрические заряды, находящиеся на различных каплях, являются целыми кратными очень небольшого количества электричества — элементарного электрического заряда. Тело может быть заряжено количеством электричества, равным лишь целому кратному элементарного заряда.
 [58]

Тогда заряд капли, а с ним и скорость установившегося движения в воздухе в том же электрическом поле могут скачком измениться. Если капля мала, а электричество имеет атомистическое, дискретное строение, то можно ожидать, что заряд капли состоит из небольшого числа элементарных зарядов.
 [59]

При q qKp, поскольку возникшая деформация продолжает увеличиваться — капля неустойчива. Процесс кончается расщеплением неустойчивой капли на две или большее количество) более мелких устойчивых капель. С уменьшением размеров капли критический заряд qk уменьшается пропорционально корню квадратному из ее объема, в то время как заряд капли q уменьшается в среднем пропорционально объему; поэтому при достаточно малых размерах капли условия устойчивости начинают выполняться.
 [60]

Страницы:  

   1

   2

   3

   4