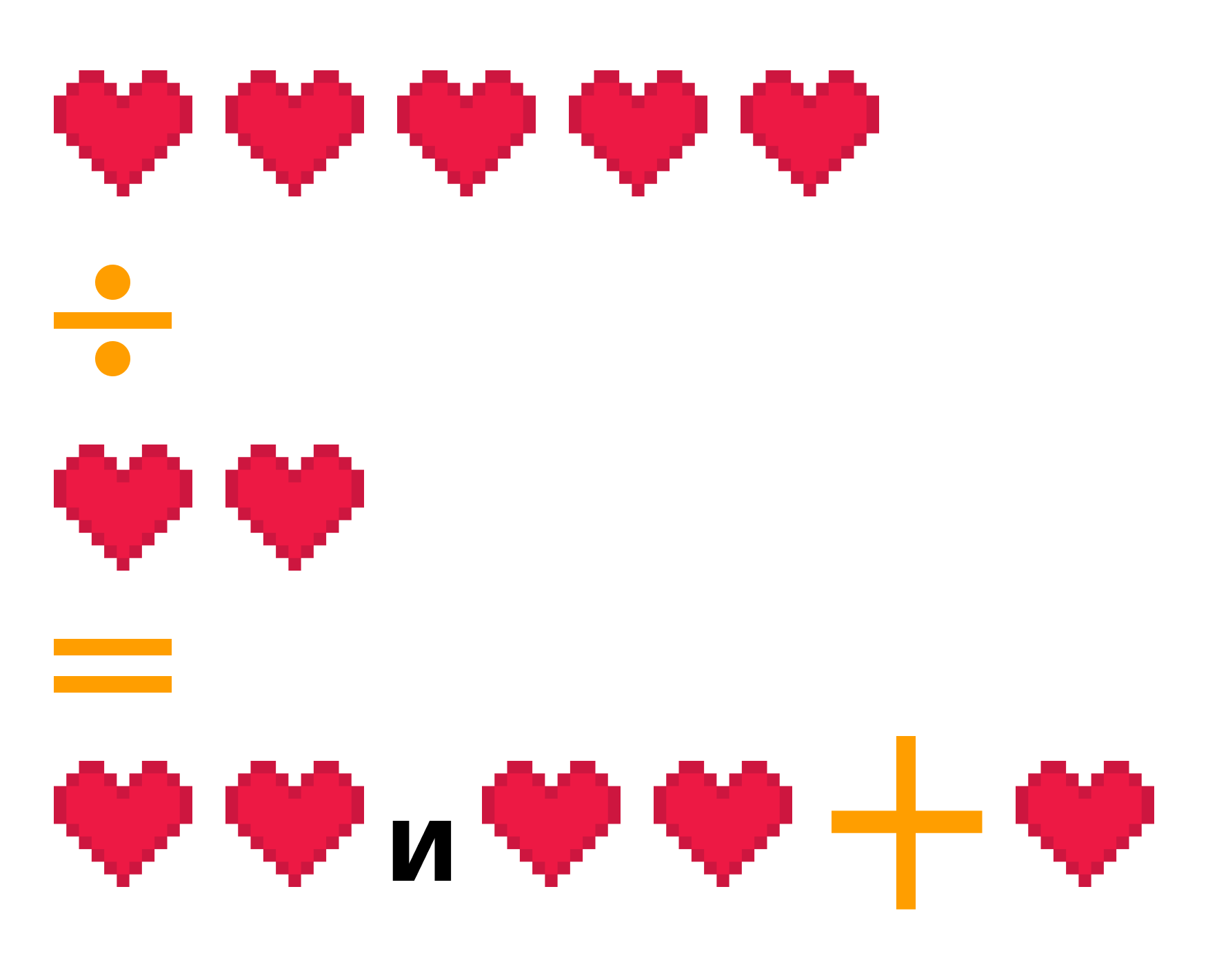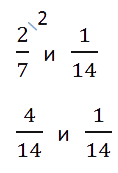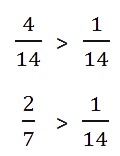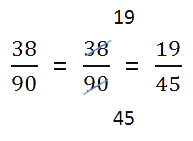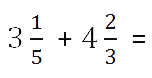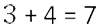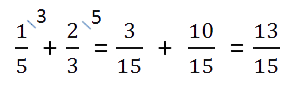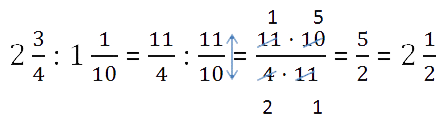Как найти четные дроби

Раздел:
Уроки

В блог
Подписаться на Дзен!

Отвечать в конференциях и заводить новые темы может любой участник, независимо от наличия регистрации на сайте 7я.ру.

Четные и нечетные числа. Понятие о десятичной записи числа

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция

Результат

Пример

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция

Результат

Пример

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все десятичные дроби.

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Источник

Четные и нечетные числа

О чем эта статья:

Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.

Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.

Четное число — это число, которое делится нацело на 2.

4 : 2 = 2
Это значит, что 4 — четное число.

Нечетное число — это число, которое не делится на 2 без остатка.

5 не делится на 2 без остатка — значит, 5 это нечетное число.

Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.

Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.

Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.

Свойства четных и нечетных чисел

• Если сложить два четных числа, получится четное число:
  8 + 8 = 16
  16 : 2 = 8
• Если сложить два нечетных числа, получится четное число:
  3 + 3 = 6
  6 : 2 = 3
• Если сложить четное число с нечетным, получится нечетное число:
  4 + 5 = 9
  9 : 2 = 4 (остаток 1)
• Если четное число умножить на четное число, получится четное число:
  2 × 2 = 4
  4 : 2 = 2
• Если четное число умножить на нечетное число, получится четное число:
  4 × 3 = 12
  12 : 2 = 6
• Если нечетное число умножить на нечетное, получится нечетное:
  3 × 3 = 9

Четные и нечетные числа чередуются друг с другом

1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.

Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.

1	11	21	31	41	51	61	71	81	91
2	12	22	32	42	52	62	72	82	92
3	13	23	33	43	53	63	73	83	93
4	14	24	34	44	54	64	74	84	94
5	15	25	35	45	55	65	75	85	95
6	16	26	36	46	56	66	76	86	96
7	17	27	37	47	57	67	77	87	97
8	18	28	38	48	58	68	78	88	98
9	19	29	39	49	59	69	79	89	99
10	20	30	40	50	60	70	80	90	100

Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.

Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.

Задачи для практики

Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.

Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?

1	♥	17
2	10	♥
♥	11	19
4	♥	20
5	13	♥
♥	14	22
7	15	23
8	♥	♥

Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.

Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.

X	2	4	6	8	10
X × 2
X : 2

X	2	4	6	8	10
X × 2	4	8	12	16	20
X : 2	1	2	3	4	5

2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное

Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?

Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)

Отнимем от общего количества конфет получившееся число:
44 — 27 = 17 (к)

Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.

Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?

51 — 5 = 46 (ф)
46 — четное число.

Ответ: изначально у Маши в инстаграме было 46 фотографий.

Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.

1	☆	3	☆	5
6	☆	☆	9	10
☆	12	13	☆	15
16	☆	☆	19	20
☆	22	23	☆	25

Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.

Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70

Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.

Источник

Обыкновенные дроби

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Виды дробей:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

1. В обеих дробях знаменатель равен 5.
2. В первой дроби числитель равен 1, во второй дроби равен 4.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к наименьшему общему знаменателю (НОЗ);
• сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

1. Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Найдем наименьшее общее кратное для определения единого делителя.

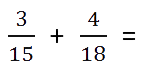
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

Полученные числа запишем справа сверху над числителем.

Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

Проверим полученный результат:

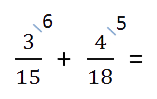
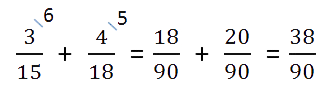
• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.
   
   
2. Сложить дробные части.
   

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Суммировать полученные результаты.

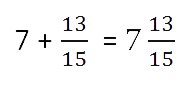
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

1. преобразовать смешанные дроби в неправильные;
2. перемножить числители и знаменатели дробей;
3. сократить полученную дробь;
4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

Источник

Adblock
detector

There is a natural way to define «oddness» for fractions. For integer $x$, let $nu_{2}(x)$ denote the number of $2$’s that divide $x$. For example, $nu_2(6)=1, nu_2(4)=2, nu_2(12)=2, nu_2(1)=0, nu_2(7)=0$. We can leave $nu_2(0)$ undefined, or set it equal to $infty$, as you like.

We can extend this to fractions via $$nu_2left(frac{m}{n}right)=nu_2(m)-nu_2(n)$$

This satisfies the lovely relation $$nu_2(xy)=nu_2(x)+nu_2(y)$$
which holds even when $x,y$ are fractions.

With this tool in hand, we can define a number $x$ as «odd» if $nu_2(x)=0$. The product of two odd numbers is odd, while the product of an odd number and a non-odd number is non-odd. However there is no natural definition of «even» numbers. We could take $nu_2(x)neq 0$ (but then the product of two even numbers might be odd), or $nu_2(x)>0$ (but then we need a third term for $nu_2(x)<0$).

See also a more comprehensive answer here.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ НЕПРЕРЫВНЫХ ДРОБЕЙ, ЧЁТНЫЕ И НЕЧЁТНЫЕ ПОДХОДЯЩИЕ КОТОРЫХ ИМЕЮТ РАЗЛИЧНЫЕ ПРЕДЕЛЫ Шмойлов В.И. Email: Shmoylov681@scientifictext.ru

Шмойлов Владимир Ильич — старший научный сотрудник, Научно-исследовательский институт многопроцессорных вычислительных систем Южный федеральный университет, г. Таганрог

Аннотация: для вычисления значений непрерывных дробей с вещественными элементами предлагается использовать r/и-алгоритм. В этом случае при вычислении значений подходящих дробей всякий раз конечная непрерывная дробь должна иметь последним звеном вещественное число еи, именуемое гиперболическим маркером. С помощью r/и-алгоритма устанавливаются значения расходящихся в классическом смысле непрерывных дробей, чётные и нечётные подходящие которых имеют различные пределы.

DETERMINING THE VALUES OF CONTINUOUS FRACTIONS WHOSE EVEN AND ODD VALUES HAVE DIFFERENT LIMITS

Shmoylov V.I.

Shmoilov Vladimir Ilyich — Senior Researcher, RESEARCH INSTITUTE OF MULTIPROCESSOR COMPUTING SYSTEMS SOUTHERN FEDERAL UNIVERSITY, TAGANROG

Abstract: to calculate the values of continued fractions with real elements, it is proposed to use the r/u-algorithm. In this case, when calculating the values of suitable fractions, each time a finite continuous fraction must have a real number еи at the last link, called a hyperbolic marker. Using the r/u-algorithm, we establish the values of continuous fractions in the classical sense of which even and odd suitable fractions have different limits. Keywords: divergent continued fractions, r/u-algorithm, hyperbolic marker method.

УДК 517.524

1. Непрерывные дроби с частными числителями, включающими показательную функцию вещественной переменой Степенной ряд

1 + схх + с2 х 2 + с3X3 + —I- спхп + • • • представляется так называемой соответствующей непрерывной дробью

1-1 + 1 —-+ 1-1 +•••

Коэффициенты о & непрерывной дроби по коэффициентам с& исходного степенного ряда могут быть установлены по формулам Хейлерманна-Стилтьеса или рекуррентным алгоритмом Рутисхаузера [1]. Полагая х = е& *, будем иметь ряд

1 + схе&* + с 2е& 2 * + с 3е& 3 * + • • • + спе&п * + • • • , для которого соответствующая непрерывная дробь имеет вид:

^ ^ ^ ^ owe^ 1-1 + 1-1 +—- 1+1 —-.

Если х = е», то для ряда

1 + схе» + с2е2 » + с з е3 » + • • • + спепи + • • •

соответствующая непрерывная дробь записывается следующим образом:

шлеи со?еи со-,еи со4еи со?Г1еи о)7и+1еи

— _J— 2n —^— (1)

1-1 + 1-1 +•••- 1+1 -•••.

Подходящими дробями непрерывной дроби (1) будет последователь-ность вещественных чисел:

{Р„/ Çn}„=! = {гхеи 1,Г2е»2…..гпе»п,. . .} . (2)

2. Определение значений периодических непрерывных дробей с элементами re11

Рассмотрим определение значений периодической непрерывной дроби, каждый частный числитель которой содержит показательную функцию действительного переменного :

геи геи геи

1 +-+-+„.+—+„, (3)

Периодические непрерывные дроби — это сходящиеся непрерывные дроби, которые определяются значением вещественного или комплексного корня квадратного уравнения. Если корень квадратного уравнения, который представляет периодическая непрерывная дробь — комплексный, то значение расходящейся в классическом смысле непрерывной дроби устанавливается г/р-алгоритмом [2], Разнообразные применения r/^-алгоритма рассмотрены в работах [3 — 14].

Значение периодической непрерывной дроби (3) определяется корнем квадратного уравнения

х2 — х — геи = 0.

Для подходящих периодической непрерывной дроби (3) можно записать:

Рп геи

— = 1 +-.

Qn Pn-i/Qn-i

Значение непрерывной дроби (3) будем искать в виде

со = г0еи°.

Р1 геи

— = 1 + —— = 1 + r{ch и + shu) = 1 + rchu + rshu = r±eUl.

Обозначая

1 + r chu = a, r shu = b,

определим значения и :

rx = ^a2 — b2 = д/(1 + r ch u)2 — (r sh u)2,

щ = Arth — = Arth——.

a 1 + r chu

Вычисление значений подходящих непрерывной дроби (3) с «гиперболическими» элементами г е» предполагает выполнения ряда операций.

1. Составляется выражение

р ге» геи TT» = 1 + -^-= 1 +-■

Qn Pn-t/Qn-t Гп_^ип-1

2. Выполняется деление двух чисел, записанных в показательной форме:

— = 1 +-e»-«n-i = 1 + rne»n.

Qn ^n—1

3. Число е» п записывается по формуле Эйлера, а значение Р„/ Ç„ представляется в

показательной форме: рп

— = 1 + r&n(chu&n + shu&n) = 1 + r&nchu&n + r&nshu&n = rneUn.

гп = 7(1 +Гпс и пу — (г nSh.il&пу, ип = АПК — г 11

1 + г пскип

Значение подходящей дроби Рп/<3п в показательной форме используются далее при определении следующей подходящей дроби:

Р„+1 геи геи

= 1 +-= 1 + ——.

(¿п+1 Рп/Яп гпеип

Таким образом, получается последовательность подходящих {гпе»п} непрерывной дроби (3).

3. Примеры определения значений периодических непрерывных дробей с

«гиперболическими» элементами

Запишем непрерывную дробь с «гиперболическими» элементами:

2еи 2еи 2еи

1 +- — — . (4)

1 + 1 +•••+ 1 +•••

Непрерывная дробь (4) представляет корень квадратного уравнения

_ 1 + VI + 8еи

х2 — х — 2еи = 0, х1 =-.

1 2

При и = 0 , 1 непрерывная дробь (4) определяет корень квадратного уравнения

х г-х-2 е0& 1 = 0, х1 = 2,068547683 7. . . . (5)

В табл. 1 приведены результаты вычисления непрерывной дроби (4) при и = 0, 1 , причём, значения подходящих непрерывной дроби определяются в показательной форме, т. е. = гпе»п.

2е°Д 2еод 2еод

Таблица 1. Определение значения непрерывной дроби 1 +—— ^ —— .

Номер Значения Значения Значения Значения

подходящих подходящих модуля, гп аргумента,ип произведения,

дробей, п дробей, Рп/ <3 п гпеПп

1 3.2103418361 3.0033342591 0.0666543312 3.2103418361

2 1.6885066914 1.6661487870 0.0133296760 1.6885066914

4 1.9572510843 1.9087525189 0.0250910835 1.9572510843

8 2.0603527192 1.9946474087 0.0324098938 2.0603527192

16 2.0685060251 2.0007143663 0.0333223197 2.0685060251

32 2.0685476826 2.0007408544 0.0333292192 2.0685476826

64 2.0685476837 2.0007408550 0.0333292195 2.0685476837

Из сравнения данных, приведённых в колонках 2 и 5, можно сделать вывод, что значения подходящих дробей, вычисленные двумя различными способами, а именно, — непосредственным счётом и через определение модулей гп и аргументов ип подходящих дробей , совпадают.

В табл. 2 приведены значения непрерывной дроби (4), полученные в показательной форме, т.е. х = г0еи°, при различных величинах аргумента и.

Таблица 2. Определение значений непрерывных дробей 1 + —&— —&— —&— ; х2 — х —

2еи = О

Значения аргумента, u Значения непрерывных дробей Значения модуля, r0 Значения аргумента, Значения произведения, г0е»°

0 2 2 0 2

0,2 2.1409770005 2.0029647894 0.0666337895 2.1409770005

0,4 2.2982350778 2.0118809530 0.1330713889 2.2982350778

0,6 2.4733822743 2.0268129667 0.1991219635 2.4733822743

0,8 2.6681978362 2.0478652860 0.2646053500 2.6681978362

1,0 2.8846516846 2.0751779538 0.3293572485 2.8846516846

2,0 4.3766109164 2.3122194404 0.6380668015 4.376610916

5,0 17.735902013 4.2393127158 1.4311897867 17.735902013

4. Определение значений непрерывных дробей общего вида с «гиперболическими» элементами

Речь идёт о вычислении значений непрерывных дробей вида

сгеи с2еи спеи

1+—— —— . (6) 1 + 1 +•••+ 1 +••• Так как непрерывная дробь непериодическая, то вычисления производим, начиная с последнего звена.

■тг» = 1 + ■ с2е сп- 1е спе

= 1 +

Qn 1 + 1 +•••+ 1 + 1

Iе с2е сп-2е сп-1е

1 + 1 +——+ 1 +1 + c„cftu + C„sftu

Iе с2е сп-2е сп-Iе

= 1 + , 1 + 1 +•••+ 1 +rn_1e»n-1

где г„ _ ! = V а 2_ 1 — _ 1 = 7(1 + cncftu) 2 — (c„sftu) 2,

Ьп_1 cnshu

ип_ -, = i4rtft-= i4rtft——.

an_x 1 + cnchu

Продолжая вычисления, получим:

^=1+^ —n_—f_ Cn_16 =

Çn 1 + 1 +•••+ 1 +rn_ie»n-i

= 1+—lf_ ^ fn^ —n_2 6 ,

1 + 1 +•••+ 1 +rn_2e»n-2 Чтобы найти число rn _ 2е»п- 2, надо выполнить операции деления модулей и вычитания аргументов чисел —n _ ^ и rn _ ^^е»»- ^ Выполняются также дополнительные операции:

1 + -, = 1 + r&n-2eU&n~2 = 1 + r&n.2(chu&n_2 + shu&„_2) =

1 + r&n_2chu&n_2 + r& n-2shu& n_2. = rn_2eUn~2.

rn-2 = — b2_2 = V(1 + r&n_2chu&n_2y — (r&n_2shu&n_2y

bn-2 . l7 Г n-2S^U n—2

un-2 = Arth-= Arth

ап-2 1 V&п-2СЬи п_2

При вычислении следующего звена непрерывной дроби выполняются аналогичные операции. Процесс повторяется, пока не будет вычислена вся непрерывная дробь, содержащая звенья вида с¿еи, и не получено значение непрерывной дроби в виде числа, представленного в показательной форме, т.е. записанного в виде .

Здесь следует остановиться на вычислительном аспекте. Дело в том, что определение значений подходящих непрерывных дробей с вещественными элементами в показательной форме требует существенных затрат. Если для вычисления одного звена вещественной непрерывной дроби необходимо выполнения всего двух арифметических операций, — деления и сложения, то при вычислении одного звена с числами, представленных в показательной форме, требуется 13 операций, причём, среди этих 13-ти операций четыре операции связаны с вычислением значений элементарных функций, а именно, — с определением значений гиперболических косинуса, синуса и арктангенса, а также с определением значения квадратного корня. Вычисления значений элементарных функции сопряжены с выполнением множества арифметических операций.

По последовательности подходящих дробей непрерывной дроби (6), представленных в показательной форме

{г1еи1,г2е»2, …,гпеип,…}, запишем две вещественные последовательности, — последовательность модулей и последовательность аргументов .

Аналогично тому, как для определения значений непрерывных дробей с комплексными элементами

с1е1<р с2е1гр спе1(р

1+1 + 1 +•••+ 1 +•••

в [15] был предложен г/р(5)-алгоритм, введём для определения значений непрерывных дробей с элементами с¿е» г/и-алгоритм, формулируемый следующим образом:

Непрерывная дробь с элементами с^е»

слеи с7еи с„еи

1+-1 2 п

1 + 1 +•••+ 1 +•••

сходится и имеет своим значением число со = г0еи0, если существуют пределы

г0 = Ii туП=1 гп, (7)

Щ+и2 +—-1-ип

и 0 = Ii т-, (8)

п-> п

где гп — значения модуля -й подходящей дроби в показательной форме, ип — величина аргумента -й подходящей дроби.

5. Примеры определения значений непрерывных дробей общего вида с элементами с¿еи

В табл. 3 приведены результаты вычисления г/и-алгоритмом непрерывной дроби

с с с

1 + —— —— 1 + 1 +•••+ 1 +•••

при с = п, i = 1 ,2 , 3 ,. . ., и = 1 . Значения подходящих дробей определяются в показательной форме, т.е. Рп/Qn = гпеип.

Номер подходящих дробей, n Значения подходящих дробей, Рп/ Q п Значения модуля, гп Значения аргумента, ип Значения произведения, rneUn

1 3.7182818284 2.2552519304 0.5 3.7182818284

2 1.4223187982 1.3129231736 0.0800324148 1.4223187982

3 2.7054864189 1.8554983069 0.3771284291 2.7054864189

4 1.6436937230 1.4298628423 0.1393674541 1.6436937230

7 2.2423024424 1.6772565583 0.2903437564 2.2423024424

8 1.8473425486 1.5209728985 0.1943979512 1.8473425486

127 2.0112980984 1.5875766319 0.2365716109 2.0112980984

128 2.0112827647 1.5875705803 0.2365677990 2.0112827647

255 2.0112902538 1.5875735360 0.2365696608 2.0112902538

256 2.0112902009 1.5875735151 0.2365696477 2.0112902009

Из рассмотрения табл. 3 следует, что непрерывная дробь (9) сходится в классическом смысле, так как значения подходящих дробей с чётными и нечётными индексами сходятся к одному и тому же пределу, — вещественному числу 2,0112902…

Известна непрерывная дробь для неполной гамма-функции [16]:

ч x a | 1 1-a 1 2 — a n n + 1 — a

Y(a, x) = e xa I- — — — — ^ x + 1 + x + 1 +… + x + 1 + ..J

При a = l / 2 и x = l / 2 после преобразований этой непрерывной дроби получим:

1 + i234 m = ^ , = 1,5251352761….

1 + 1 + 1 + 1 +… + 1 +… Ц1/2, 1/2)

Сходится в классическом смысле и непрерывная дробь, содержащая квадраты

натуральных чисел:

I2 22 З2 п2 1

l+— — — — = — = l ,442 69 5 0. . . . (10)

1 + 1 + 1 + •••+ 1 Ы2

Непрерывная дробь (10) сходится столь же медленно, как и ряд Лейбница. Для ряда Лейбница равноценной непрерывной дробью будет непрерывная дробь: _ 1111 _ 1 12 22 32 2

2 = 1 ~ 2 +3~4 +&&& = 7 + 7 + 7 + 7 + — • -+Т+- • • .

Запишем непрерывную дробь, частные числители которых являются кубами натуральных чисел:

73 23 33 3

1+- — — — . (11) 1 + 1 + 1 +-• •+ 1 +-• •

Непрер^1вная дробь (11) является расходящейся в классическом смысле, так как значения чётных и нечётных подходящих дробей стремятся к различным пределам [17]:

lim = 1,50202064 …, р

lim — = 1,26465247….

Известны многочисленные публикации, посвящённые непрерывным дробям, имеющим различные значения пределов подходящих дробей с чётными и нечётными индексами [18 — 20].

Определим значение расходящейся в классическом смысле непрерывной дроби (11) г/м-алгоритмом, используя формулы (7) и (8), предварительно записав непрерывную дробь (11) в эквивалентной форме (12).

В табл. 4 показаны результаты определения значения непрерывной дроби (11), коэффициенты которой представлены в показательной форме.

Таблица 4. Определение значений подходящих дробей —е03 — е03 — е03 — е0-5

1 + 1 + 1 +…+ 1 +…& ^ &

Номер подходящих дробей,п Значения подходящих дробей, Р„/а„ Значения модуля, гп Значения аргумента, ип Значения произведения, гпеип

1 2 1.6540129631 0.1899427465 1.9999999999

2 1.1111111111 1.1021688395 0.0080806047 1.1111111111

3 1.7777777777 1.5142890818 0.1604180689 1.7777777777

4 1.1503267973 1.1344825672 0.0138694145 1.1503267973

7 1.6640433274 1.4441510949 0.1417287087 1.6640433274

8 1.1838069034 1.1604535043 0.0199245541 1.1838069034

16383 1.5042969144 1.3490354905 0.1089357369 1.5042969144

16384 1.2631567966 1.2159665015 0.0380747467 1.2631567966

32767 1.5036170511 1.3486444098 0.1087736257 1.5036170511

32768 1.2636024799 1.2162541316 0.0381910010 1.2636024799

Из табл. 4 следует, что подходящие непрерывной дроби (12) с чётными и начётными индексами стремятся к различным пределам.

В табл. 5 показаны результаты определения значения непрерывной дроби (12) с помощью г/м-алгоритма, т.е. формул (7) и (8).

Таблица 5. Определение значения непрерывной дроби г/м-алгоритмом

^1е05 ^1е0.5 ^1е0.5 л1ео.5

^ | е05 е05 е05 е0.5е

1 + 1 + 1 +•••+ 1 +…

Номер подходящих дробей,п Значения модуля, гп Значения аргумента, ип Значения (п) модуля, г0 Значения (п) аргумента, и;, Значения произведения, х0 = ГдП^еи°

1 1.6540129631 0.1899427465 1.6540129631 0.1899427465 1.9999999999

2 1.1021688395 0.0080806047 1.3501857458 0.0990116756 1.4907119849

3 1.5142890818 0.1604180689 1.4028092131 0.1194804734 1.5808414686

4 1.1344825672 0.0138694145 1.3302963939 0.0930777086 1.4600628440

7 1.4678099220 0.1484205321 1.3567277090 0.1041462733 1.5056459029

8 1.1604535043 0.0199245541 1.3135726835 0.0874819092 1.4336628079

16383 1.3490354905 0.1089357369 1.2809179170 0.0735958505 1.3787437992

16384 1.2159665015 0.0380747467 1.2809138487 0.0735936825 1.3787364310

32767 1.3486444098 0.1087736257 1.2808358951 0.0735438165 1.3785837779

32768 1.2162541316 0.0381910010 1.2808338728 0.0735427376 1.3785801139

6. Алгоритм определение значений непрерывных дробей с вещественными элементами

В 1994 г. был предложен алгоритм суммирования непрерывных дробей [2], получивший название г/^-алгоритма. Этот алгоритм формулируется следующим образом:

Непрерывная дробь с вещественными элементами сходится и имеет своим

значением в общем случае комплексное число = , если существуют пределы:

г=11ш «п|/> / а|, (13)

|РоМКш кп, (14)

п^да п

где / — значение -й подходящей дроби,

кп — количество подходящих дробей, имеющих отрицательные значения, из

совокупности, включающей п подходящих дробей.

В [21] было показано, что комплексное значение непрерывной дроби с вещественными элементами

С-1 Су С71

1-— — — (15)

1 — 1——1 -••• v 7

может быть найдено не только г/ф-алгоритмом, описываемого формулами (13) и (14), но и при помощи г/ф^)-алгоритма, предложенного в [15] для определения значений непрерывных дробей с комплексными элементами, который формулируется следующим образом:

Непрерывная дробь с комплексными элементами

г р1<Р г р1<Р г рЩ

1 + с^ (16)

1 + 1 +•••+ 1 +•••

сходится и имеет своим значением комплексное число , если

существуют пределы

г0 = 11ш

П Гп , (17)

I | ,• т++…+\фА (18)

ф0 = 11Ш ]—!—!—!-1—-, (18)

п^да п

где — значение модуля комплексной подходящей непрерывной дроби,

— абсолютная величина аргумента комплексной подходящей дроби. Как можно заметить, г/ф^)-алгоритм отличается от г/ф-алгоритма в способе определения аргумента комплексного числа г = г0е&р 0. Если в г/ф-алгоритме аргумент находится из анализа знаков вещественных подходящих дробей, то есть используется формула (14), то в г/ф^)-алгоритме аргументы <рп имеются в последовательности комплексных подходящих дробей {гпе1 &Рп}. Значение аргумента , точнее, абсолютной величины аргумента , определяется как предел средне арифметических абсолютных величин аргументов <рп при п — с», т. е. устанавливается по формуле (18). Модуль г0 комплексного числа г = г0 е & ^ 0 находится в г/ф-алгоритме и г/ф^)-алгоритме по схожим формулам, соответственно, по формулам (13) и (17), как пределы средне геометрических величин «отсчётов». Если в г/ф-алгоритме «отсчётами» являются абсолютные величины подходящих исходной непрерывной дроби, значение которой находится, то в г/ф^)-алгоритме в качестве «отсчётов» выступают значения модулей комплексных чисел ,

являющихся значениями подходящих дробей.

Чтобы устанавливать комплексное значение непрерывной дроби (15) с вещественными элементами при помощи г/ф^-алгоритма, т.е. формул (17) и (18), необходимо, чтобы подходящие непрерывной дроби (15) имели комплексные значения. Этого можно достичь, если подходящие непрерывной дроби (15) с

вещественными элементами записывать всякий раз с последним звеном, включающим комплексную величину е& называемую маркером комплексности:

Р2 с, с 2е1ч>

Ру. _ Л _ £1 сп-1 спе1,р _ (2„~ 1 — 1—— 1 — 1 ~Гп6 «■

где .

Такой метод непосредственного определения комплексных значений непрерывных дробей с вещественными элементами в [21] был назван методом комплексного маркера.

7. Определение значений непрерывных дробей с вещественными элементами методом гиперболического маркера

Выше был рассмотрен г/ц-алгоритм, используемый для определения значений непрерывных дробей с вещественными элементами, который может устанавливать, как вещественные, так и комплексные их значения. Комплексные значения непрерывных дробей с вещественными элементами могут определяться не только г/ц-алгоритмом, но и методом комплексного маркера [22].

Применим для определения значений непрерывных дробей с вещественными элементами гиперболический маркер е», где и — некоторое вещественное число. Введение гиперболического маркера подразумевает, что подходящие непрерывной дроби с вещественными элементами

1+— — — (19)

1 + 1 + • • •+ 1 + • • •

всякий раз в последнем звене содержат вещественное число . Таким образом, при использовании гиперболического маркера подходящие непрерывной дроби (19) имеют вид:

Р1 с±еи

■7Г = 1 + Л» = Ъе»1, (¿1 1 и Рп С-1 Сп 6

— = 1 + _ __ = г р»2

<?2 1 + 1 + 1 Г2е & (20)

= 1 + с»~1 с»е _ г еип

<2„ 1 + 1 + •••+ 1 + 1 » &

Сходимость непрерывных дробей (19), подходящие которых записываются с гиперболическим маркером е», определяются г/и-алгоритмом, т.е. формулами (7) и (8), аналогично тому, как была определена этим алгоритмом сходимость непрерывных дробей (6) с частными числителями с &е». Сходимость непрерывных дробей, подходящие которых записываются в показательной форме ,

обуславливается существованием пределов модулей и аргументов ,

устанавливаемых г/и-алгоритмом.

8. Примеры суммирования непрерывных дробей при помощи гиперболического маркера

Определим с помощью гиперболического маркера значение непрерывной дроби

2 2 2 1+- — — . (21) 1 + 1 + — + 1 + Используя гиперболический маркер е» при и = 1, запишем подходящие непрерывной дроби (21):

а = 1+т

Р2 2 2е 2

— = 1 +- — = 1 +-,

(1г 1+1 Р1/<21

Рп 2 2 2 2е 2

— =1+- — — —=1+-.

(¿п 1 + 1 +-+ 1+1 Р„-1/<г„-1

В табл. 6 приведены результаты вычисления периодической непрерывной дроби (21) с использованием гиперболического маркера.

Таблица 6. Определение значения непрерывной дроби с маркером Рп _ 2 2 2 2е 0^~1 + 1 + 1 + — + 1+~

Номер подходящих дробей, п Значения подходящих дробей, Рп/(?.п Значения модуля, гп Значения аргумента, ип Значения произведения, гпе»п

1 6.4365636569 3.3425024366 0.6552750450 6.4365636569

2 1.3107248069 1.6795791711 -0.247962996 1.3107248069

3 2.5258733101 2.2075063390 0.1347233432 2.5258733101

4 1.7918053498 1.9103151158 -0.064044523 1.7918053498

15 2.0001092424 2.0000457774 0.0000317313 2.0001092424

16 1.9999453817 1.9999771120 -0.000015865 1.9999453817

31 2.0000000016 2.0000000006 0.0000000004 2.0000000016

32 1.9999999991 1.9999999996 -0.000000000 1.9999999991

В табл. 7 рассмотрены погрешности в определении значений непрерывной дроби (21) с вещественными элементами в зависимости от аргумента и маркера. В третьей колонке табл. 7 указано число звеньев дроби для вычисления её значения с точностью до десятого знака.

Таблица 7. Определение значений непрерывных дробей с маркерами Рп _ 2 2 2 2еи ^»1 + 1 + 1 + — + 1+~

Значения, аргумента и Значения произведения, г0е»° Количество звеньев

0,000001 2 53

0,001 2 53

0,1 2 53

1 2 55

2 2 55

1 2 55

Из третьей колонки табл. 7 следует, что значение аргумента комплексного маркера не оказывает существенного влияния на скорость определения значения непрерывной дроби в показательной форме.

В табл. 8 приведены результаты определения значения непериодической непрерывной дроби с использованием маркера.

Таблица 8. Определение значения непрерывной дроби с маркером

рп _ ^ 1 2 3 п-1 пе

Т+ Т+ ! + … + — + — ■

Номер подходящих дробей, Значения подходящих дробей, Pn/Qn Значения модуля, гп Значения аргумента, un Значения произведения, rneUn

1 3.7182818284 2.2552519304 0.5 3.7182818284

2 1.1553624034 1.3494392139 -0.155275045 1.1553624034

3 1.8207057190 1.6595329909 0.0926879516 1.8207057190

4 1.3851208011 1.4535559484 -0.048225575 1.3851208011

7 1.5693060247 1.5493697291 0.0127852772 1.5693060247

8 1.4954967463 1.5082677276 -0.008503368 1.4954967463

127 1.5251352776 1.5251352774 0.0000000001 1.5251352776

128 1.5251352747 1.5251352750 -0.000000000 1.5251352747

Из табл. 8 следует, что непрерывная дробь, частные числители которых числа натурального ряда

12 3

1+- — — — , (22)

1 + 1 + ! + •••+ 1 +••• сходится в классическом смысле.

9. Определение значений расходящихся в классическом смысле непрерывных дробей посредством маркера

Рассмотрим суммирование расходящихся в классическом смысле непрерывных дробей с вещественными элементами. Речь идёт о расходящихся в классическом смысле непрерывных дробях

1+ С-1 С-2 (23)

1 + 1+-• •+ 1 + • • •, у &

подходящие дроби с чётными и нечётными индексами которых имеют различные пределы:

lim-= а0,

fc^oo Q2k_1

.. P2k D

lim — = ß0.

k^CO Q2k

В табл. 9 приведены результаты определения значения расходящейся в

классическом смысле непрерывной дроби

13 23 33 3

1+- — — — (24)

1 + 1 + 1 +• • •+ 1 +• • • с использованием r/i^-алгоритма, описываемого формулами (13) и (14). Из формулировки r/^-алгоритма следует, что значение непрерывной дроби с вещественными элементами в общем случае представляется комплексным числом = , аргумент которого устанавливается формулой (14), т.е. «процентом»

подходящих дробей, имеющих отрицательные значения из общего числа рассматриваемых подходящих дробей. Если по формуле (14) равно нулю, то значением непрерывной дроби является вещественное число, устанавливаемое по формуле (13) r/^-алгоритма.

3 21 31 — 1 + 1 + 1 + 1 +• • •+ 1 +• • •■

Номер подходящих дробей, Значения подходящих дробей, Рп/ Значения модуля, гп Значения аргумента,

1 2 2 0

2 1.1111111111 1.4907119849 0

3 1.7777777777 1.5808414686 0

4 1.1503267973 1.4600628440 0

7 1.6640433274 1.4734245359 0

8 1.1838069034 1.4336628079 0

262143 1.5025636353 1.3783507560 0

262144 1.2642947932 1.3783503019 0

524287 1.5023957490 1.3783154775 0

524288 1.2644053248 1.3783152507 0

Значение непрерывной дроби (24), определённое при помощи г/р-алгоритма, т.е. формул (13) и (14), равно вещественному числу 1,378235 … .

В табл. 10 и 11 приведены результаты суммирования расходящейся в классическом смысле непрерывной дроби (24) методом гиперболического маркера.

Таблица 1 . Определение подходящих непрерывной дроби с маркером Рп _ I3 23 З3 (п-1)3 п3е

1+Т + Т + Т+-+ 1 + 1

Номер подходящих дробей, Значения подходящих дробей, Рп/<2п Значения модуля, Значения аргумента, ип Значения произведения, гпе»п

1 3.7182818284 2.2552519304 0.5 3.7182818284

2 1.0439632817 1.1439950171 -0.091502219 1.0439632817

3 1.9029050910 1.7325532569 0.0937855222 1.9029050910

4 1.1260949067 1.1662924520 -0.035074060 1.1260949067

7 1.6877704607 1.6480855435 0.0237940662 1.6877704607

8 1.1757224025 1.1900184363 -0.012086030 1.1757224025

32767 1.5036170827 1.5036170240 0.0000000390 1.5036170827

32768 1.2636024592 1.2636024977 -0.000000030 1.2636024592

65535 1.5031386313 1.5031386106 0.0000000137 1.5031386313

65536 1.2639166387 1.2639166522 -0.000000010 1.2639166387

В табл. 11 приведены результаты определения значения расходящейся в классическом смысле непрерывной дроби (24) с использованием г/и-алгоритма, т.е. формул (7) и (8).

3 21 31 — 1 + 1 + 1 + 1 + • • •+ 1 + • • •

Номер подходящих дробей, Значения модуля, гп Значения аргумента, un Значения (п) модуля, Значения (п) аргумента, Значения произведения, х0 = ГдП^еи°

1 2.2552519304 0.5 2.2552519304 0.5 3.71828 18284

2 1.1439950171 -0.091502219 1.6062368974 0.2042488903 1.9702156480

3 1.7325532569 0.0937855222 1.6472844410 0.1674277676 1.9475183215

4 1.1662924520 -0.035074060 1.5110481851 0.1168023107 1.6982628624

7 1.6480855435 0.0237940662 1.4989578593 0.0733719954 1.6130746876

8 1.1900184363 -0.012086030 1.4563305395 0.0626897422 1.5505499665

16383 1.5042968373 0.0000001110 1.3787528978 0.0000330487 1.3787984646

16384 1.2631568471 -0.000000086 1.3787455290 0.0000330467 1.3787910927

32767 1.5036170240 0.0000000390 1.3785883242 0.0000165274 1.3786111089

32768 1.2636024977 -0.000000030 1.3785846601 0.0000165269 1.3786074441

Заключение

Таким образом, значение расходящейся в классическом смысле непрерывной дроби

13 23 33 3

1 +— — — — = 1,378235… , 1 + 1 + 1 + • • •+ 1 +• • • пределы подходящих которой с чётными и нечётными индексами имеют различные значения, установлено тремя способами.

Наиболее точное значение непрерывной дроби (24) получено г/р-алгоритмом (табл. 9), вследствие того, что этот алгоритм даёт возможность получать значительное число подходящих дробей. Близкие значения расходящейся в классическом смысле непрерывной дроби (24) установлены г/и-алгоритмом при использовании подходящих дробей, записанных в показательной форме (табл. 5 и табл. 11).

Проводя сравнения суммирования непрерывных дробей, имеющих различные пределы подходящих с чётными и нечётными индексами, с суммированием непрерывных дробей, имеющих комплексные значения, можно отметить, что при суммировании непрерывных дробей, имеющих комплексные значения, эти значения могут быть достаточно легко устанавлены независимым путём. Например, записывая непрерывную дробь для , можем получить её комплексное значение г/ралгоритмом и сравнить это значение со значением , полученным по известным

формулам. Независимое же определение значений непрерывных дробей с двумя пределами подходящих реализовать значительно сложнее. Одним из вариантов такой проверки можно рассматривать решение расходящихся СЛАУ с соответствующими трёхдиагональными матрицами.

Список литературы /References

1. РутисхаузерГ. Алгоритм частных и разностей. М.: ИИЛ, I960. 93 с.

2. Шмойлов В.И. Суммирование расходящихся цепных дробей. Львов: ИППММ НАН Украины, 1997. 23 с.

3. Шмойлов В.И., Коровин Я.С. Непрерывные дроби. Библиографический указатель. Ростов-на-Дону: Изд-во ЮФУ, 2017. 382 с.

4. Шмойлов В.И. Непрерывные дроби. В 3 т. Том 1. Периодические непрерывные дроби. Нац. акад. наук Украины, Ин-т приклад. проблем механики и математики. Львов, 2004. 645 с.

5. Шмойлов В.И. Непрерывные дроби. В 3 т. Том 2. Расходящиеся непрерывные дроби. Нац. акад. наук Украины. Ин-т приклад. проблем механики и математики. Львов, 2004. 558 с.

6. Шмойлов В.И. Непрерывные дроби. В 3 т. Том 3. Из истории непрерывных дробей. Нац. акад. наук Украины. Ин-т приклад. проблем механики и математики. Львов, 2004. 520 с.

7. Шмойлов В.И. Непрерывные дроби и г/-алгоритм. Таганрог: Изд-во ТТИ ЮФУ, 2012. 608 с.

8. Кириченко Г.А., Шмойлов В.И. Алгоритм суммирования расходящихся непрерывных дробей и некоторые его применения. // Журнал вычислительной математики и математической физики, 2015. Т. 55. № 4. С. 559-572.

9. Гузик В.Ф., Ляпунцова Е.В., Шмойлов В.И. Непрерывные дроби и их применение. М.: Физматлит, 2015. 98 с.

10. Шмойлов В. И., Коровин Я.С. Решение систем линейных алгебраических уравнений непрерывными дробями. Ростов-на-Дону: Изд-во ЮФУ, 2017. 383 с.

11. Шмойлов В.И., Коровин Я.С., Иванов Д.Я. Непрерывные дроби и суммирование рядов. Ростов-на-Дону: Изд-во ЮФУ, 2018. 524 с.

12. Козлов В.В. Об одной формуле суммирования расходящихся непрерывных дробей. // Докл. РАН, Том 474, Номер 4, 2017. С. 410-412.

13. Шмойлов В.И., Коровин Я.С., Иванов Д.Я. Алгоритмы определения комплексных решений БСЛАУ с трёхдиагональной матрицей. // Вестник науки и образования. №9 (45). 2018. С. 6-18.

14. Шмойлов В. И., Коровин Я.С., Иванов Д.Я. Решения расходящихся систем линейных алгебраических уравнений. // Вестник науки и образования. №9 (45). 2018. С. 18-30.

15. Шмойлов В.И., Коровин Я.С. Определения бесконечных комплексных последовательностей. // Вестник науки и образования. №4 (58). 2019. С. 10-23.

16.Хованский А.Н. Приложения цепных дробей и их обобщений к вопросам приближённого анализа. М.: ГИТТЛ, 1956. 203 с.

17. Шмойлов В.И., Слобода М.З. Расходящиеся непрерывные дроби. Львов: Меркатор, 1999. 820 с.

18. Koch H. Sur a co verge ce des determi a ts d&ordre i fi i et des fractio s co ti ues. C.R.Acad.Sci. Paris, 120 (1895), 144-147.

19. Стилтьес Т.И. Исследования о непрерывных дробях. Харьков-Киев: ОНТИ, 1936. 155 с.

20.Джоунс У., Трон В. Непрерывные дроби. Аналитическая теория и приложения. Пер. с англ. М.: Мир, 1985. 414 с.

21. Шмойлов В.И. Определение значений расходящихся в классическом смысле непрерывных дробей посредством маркера комплексности. // Вестник науки и образования. № 22 (76), 2019. С. 6-17.

22. Шмойлов В.И., Коровин Я.С., Жиглатый А.А. Суммирование непрерывных дробей с вещественными элементами методом комплексного маркера. // Вестник науки и образования. № 24 (73). Часть 1, 2019. С. 6-19.