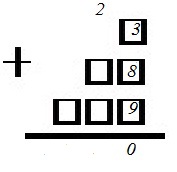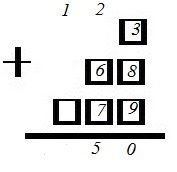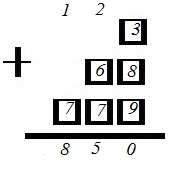Как найти четырехзначное число егэ

Всего: 68    1–20 | 21–40 | 41–60 | 61–68

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 68    1–20 | 21–40 | 41–60 | 61–68

Формулировка задачи: Найти четырехзначное число, кратное N, любые две соседние цифры которого отличаются на K. В ответе укажите любое такое число.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 19 (Задачи на цифровую запись числа).

Для решения таких задач нужно знать основные признаки делимости чисел, а также уметь раскладывать составной делитель на взаимно простые множители. Рассмотрим, как решаются подобные задачи на примере.

---

Свойства чисел

---

Задание №19 ЕГЭ по математике весьма необычно. Для его решения необходимо применить знания в области теории чисел. Тем не менее, задание является весьма решаемым, однако для школьников с оценкой хорошо и ниже я рекомендовал бы оставить это задание на последнюю очередь. Перейдем к рассмотрению типового варианта.

---

Разбор типовых вариантов заданий №19 ЕГЭ по математике базового уровня

---

Вариант 19МБ1

[su_note note_color=”#defae6″]

Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь оно такое число.

[/su_note]

Алгоритм выполнения:

1. Ввести условные обозначения.
2. Записать условия с помощью условных обозначений.
3. Преобразовать полученные выражения.
4. Логически рассуждая перебрать все возможные варианты, проверить их соответствие условиям.

Решение:

Обозначим первую цифру числа x, а вторую – y. Тогда третье число с учетом суммы цифр равной 20 будет равно 20 – (x + y). (x + y) обязательно меньше 10, иначе сумма равная 20 не получится.

По условию сумма квадратов цифр делится на 3, но не делится на 9. Запишем сумму квадратов цифр:

x ² + y² + (20 – (x + y))²

Преобразуем полученное выражение. Преобразуем квадрат разности с учетом формулы приведения.

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(20 – (x + y))² = 400 -40(x + y) + (x + y)²

Подставим получившееся выражение в начальное, получим:

x ² + y² + (20 – (x + y))² = x ² + y² + 400 – 40(x + y) + (x + y)²

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + y)²= x² + 2xy + y²

Подставим:

x ² + y² + (20 – (x + y))² = x ² + y² + 400 – 40(x + y) + (x + y)² = x ² + y² + 400 – 40(x + y) + x² + 2xy + y²

Приведем подобные слагаемые(сложим x² с x² и y^{2 с} y²), получим:

x ² + y² + 400 – 40(x + y) + x² + 2xy + y² = 2x ² + 2y² + 2 · 200 – 2 · 20(x + y) + 2xy

Вынесем множитель 2 за скобку:

2x ² + 2y² + 2 · 200 – 2 · 20(x + y) + 2xy = 2(x ² + y² + 200 – 20(x + y) + xy)

Для удобства объединим 200 и 20(x + y) и вынесем 20 за скобку, получим:

2(x ² + y² + 20(10 – (x + y)) + xy)

Множитель 2 – четный, поэтому он никак не влияет на делимость на 3 или 9. Можем его не брать в расчет и рассматривать выражение:

x ² + y² + 20(10 – (x + y)) + xy

Предположим, что и x, и y делятся на 3. Тогда x ² + y² + xy делится на 3, а 20(10 – (x + y)) – не делится. Следовательно, и вся сумма x ² + y² + 20(10 – (x + y)) + xy на 3 не делится.

Предположим, что на 3 делится только одна цифра. Тогда, учитывая, что (x + y) обязательно меньше 10, иначе сумма равная 20 не получится, подберем возможные пары.

(3;8), (6;5), (6;7), (6;8), (9;2), (9;4), (9;5), (9;7), (9;8).

Методом подстановки проверим, соответствуют эти пары условию.

x ² + y² + 20(10 – (x + y)) + xy = 3 ² + 8² + 20(10 – (3 + 8)) + 3 · 8 = 9 + 64 – 20 + 24 = 77

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 5² + 20(10 – (6 + 5)) + 6 · 5 = 36 + 25 – 20 + 30 = 71

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 7² + 20(10 – (6 + 7)) + 6 · 7 = 36 + 49 – 60 + 42 = 67

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 8² + 20(10 – (6 + 8)) + 6 · 8 = 36 + 64 – 80 + 48 = 68

x ² + y² + 20(10 – (x + y)) + xy = 9 ² + 2² + 20(10 – (9 + 2)) + 9 · 2 = 81 + 4 – 20 + 18 = 83

x ² + y² + 20(10 – (x + y)) + xy = 9 ² + 4² + 20(10 – (9 + 4)) + 9 · 4 = 81 + 16 – 60 + 36 = 73

Ни одна из полученных сумм не удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9».

Следующие пары можно не проверять, так как они дают уже имеющиеся тройки цифр.

Предположим, что ни одна из цифр числа не делится на 3.

Возможные пары:

(4;7), (5;7), (5;8), (7;8).

Проверим:

x ² + y² + 20(10 – (x + y)) + xy = 4 ² + 7² + 20(10 – (4 + 7)) + 4 · 7 = 16 + 49 – 20 + 28 = 73

x ² + y² + 20(10 – (x + y)) + xy = 5 ² + 7² + 20(10 – (5 + 7)) + 5 · 7 = 25 + 49 – 40 + 35 = 69

Сумма 69 удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9». Следовательно, подходят цифры 5,7,8 в любом порядке.

Ответ: 578

---

Вариант 19МБ2

[su_note note_color=”#defae6″]

На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения:

1. Вспомнить признак делимости на 10.
2. Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
3. Расположить оставшиеся карточки в произвольном порядке.

Решение:

1. Если сумма делится на 10 нацело, то последняя цифра должна быть 0, остальные цифры значения не имеют.

2. В первый квадрат поместим цифру 1, в следующем числе на последнем месте – цифру 3 (или 6), а в третьем – цифру 6 (или 3), получим (сумма 1+3+6=10):

3. Остальные цифры заполним произвольно, например, так:

и получится сумма

1+23+996 = 1020.

Ответ: 1020

---

Вариант 19МБ3

[su_note note_color=”#defae6″]

На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения:

1. Вспомнить признак делимости на 10 и сформулировать признак делимости на 20.
2. Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
3. Разместить предпоследние цифры каждого слагаемого таким образом, чтобы в сумме получилось четное число в результате с учетом суммы первых цифр.
4. Расположить оставшиеся карточки в произвольном порядке.

Решение:

1. Чтобы сумма делилась на 20, она должна заканчиваться на 0 и вторая цифра с конца должна быть четной (делиться на 2). Чтобы в конце суммы получить 0, первые три карточки следует выбрать так:

2. Чтобы вторую цифру получить четной, можно взять карточки 2 и 7 (к ней будет добавляться еще 1 от первой суммы 10):

3. В последнее место помещаем оставшуюся цифру 1, в результате имеем:

и сумма равна:

2+23+175=200.

Ответ: 200

---

Вариант 19МБ4

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 15, произведение цифр которого больше 0, но меньше 25. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Если произведение >0, то, значит, оно не равно нулю. Следовательно, ни один из множителей не может быть равным 0.
2. Если произведение кратно 15, следовательно, оно кратно 5 и кратно 3.
3. Если произведение кратно 5, то результат его должен оканчиваться 0 или 5. В данном случае берем 5, т.к. 0 не может быть одним из множителей (см.п.1).
4. Итак, последняя цифра числа равна 5. Тогда произведение первых трех равно 25:5=5. Это означает, что нужно подобать 3 цифры так, чтобы их произведение было менее 5.
5. Из всех полученных наборов цифр выбираем такой, чтобы сумма этих цифр плюс 5 (последняя, 4-я цифра) была кратной 3.

Решение:

Поскольку по условию произведение всех цифр кратно 15, то оно кратно 5 и 3.

Кратность 5 означает, что последней цифрой числа может быть только 0 или 5. Но 0 в виде последней цифры означал бы, что произведение всех 4-х цифр стало бы равным 0; а это противоречит условию. Тогда последняя цифра искомого числа равна 5.

Тогда получим: x·y·z·5<25 → x·y·z<5, где x, y, z – соответственно, 1-я, 2-я и 3-я цифры искомого числа.

Меньше 5 произведение таких цифр: 1 1 1, 1 1 3, 1 1 2, 1 2 2.

Согласно признаку делимости на 3, выбираем из этих наборов такой, чтобы сумма его цифр плюс 5 делилась на 3:

1+1+1+5=8 – не подходит;

1+1+3+5=10 – не подходит;

1+2+2+5=10 – не подходит

1+1+2+5=9 – подходит.

Тогда условию задачи соответствуют числа: 1125, 1215, 2115.

Ответ: 1125, 1215, 2115

---

Вариант 19МБ5

[su_note note_color=”#defae6″]

Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно получившееся число.

[/su_note]

Алгоритм выполнения

1. Число делится на 18, если оно кратно 2 и 9.
2. Кратность 2 означает, что число должно быть четным. Поэтому сразу отбрасывают последнюю – нечетную – цифру 7.
3. Кратность 9 означает, что сумма его цифр делится на 9. Значит, находим сумму оставшихся цифр. Далее определяем подходящее для полученной суммы число, кратное 9. Число должно быть таким, чтобы: а) оно было меньшим суммы цифр; б) разница между этой суммой и найденным числом позволяла выделить в числе 2 цифры, сумма которых была бы равной этой разнице. Вычеркиваем эти цифры.

Решение:

Т.к. по условию число кратно 18, то оно кратно 2 и кратно 9.

Поскольку число кратно 2, то оно должно оканчиваться четной цифрой. 7 – нечетная цифра, поэтому вычеркиваем ее. Осталось: 8541762.

Т.к. полученное число кратно 9, то сумма его цифр должна делиться на 9. Находим общую сумму его цифр: 8+5+4+1+7+6+2=33. Ближайшее число, которое делится на 9, – это 27.

33–27=6 – это сумма двух цифр, которые нужно вычеркнуть. Пары цифр, которые при этом в сумме дают 6, – это 5 и 1 или 4 и 2. Вычеркнув их, получаем соответственно: 84762 или 85176.

Кроме этого, на 9 делится 18. Тогда 33–18=15. В этом случае вычеркнуть придется 8 и 7. Получаем: 54162.

На 9 делится еще и 9, однако 33–9=24, а пары цифр, которые дали бы в сумме 24, естественно, не существует.

Ответ: 84762, 85176, 54162

---

Вариант 19МБ6

[su_note note_color=”#defae6″]

На шести карточках написаны цифры 3; 6; 7; 7; 8; 9 (по одной цифре на каждой карточке). В выражении 

Вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20.

В ответе укажите какую-нибудь одну такую сумму.

[/su_note]

Алгоритм выполнения

1. Во 2-м предложении текста задачи фактически представлено условие, при котором сумма делится на 10, однако не делится на 2.
2. Из п.1 следует, что результирующее число должно оканчиваться 0, а предпоследняя его цифра должна быть нечетной.

Решение:

Для удобства восприятия разместим карточки в столбик:

Если число делится на 10, но не делится на 20, значит, оно точно не делится на 2 без последнего нуля.

Поскольку число кратно 10, то оно должно оканчиваться нулем. Поэтому в последнем разряде (единиц) нужно расположить 3 карточки с такими цифрами, чтоб их сумма оканчивалась на 0. Подходят здесь карточки: 1) 6, 7, 7; 2) 3, 8, 9. Их суммы равны 20. Соответственно, 0 мы пишем под чертой, а 2 переносим на предыдущий разряд (десятков):

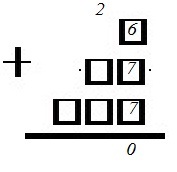
Чтобы число не делилось на 20, необходимо, чтобы перед нулем стояла нечетная цифра. Нечетная сумма здесь получится тогда, когда одно из слагаемых будет нечетным, а два других четными. Одно из этих (других) слагаемых – это перенесенная 2. Поэтому из оставшихся цифр следует взять: 1) 3 и 8; 2) 6 и 7. Получаем:

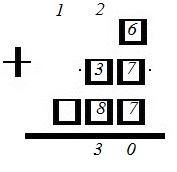
На место сотен ставим последнюю (оставшуюся) карточку с цифрой: 1) 9; 2) 7. Получаем, соответственно, числа 1030 и 850:

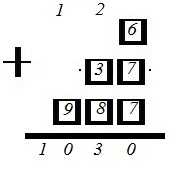
Ответ: 1030,850

---

Вариант 19МБ7

[su_note note_color=”#defae6″]

Найдите четное трехзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Вводим буквенные обозначения для цифр искомого числа. Исходя из условия задачи, составляем уравнение.
2. Выражаем одну из цифр через 2 другие.
3. Подбираем для этих 2-х (других) цифр значения так, чтобы 3-я (выраженная) представляло бы собой натуральное число. Вычисляем 3-ю цифру.
4. Формируем искомое число так, чтобы оно было четным.

Решение:

Пусть цифры искомого числа – x, y, z. Тогда получаем:

xyz–(x+y+z)=1

xyz–x–y–z=1

zxy–z=x+y+1

z(xy–1)=x+y+1

z=(x+y+1)/(xy–1)

Знаменатель в этом выражении должен быть целым и положительным. Для простоты (а также для гарантии правильных расчетов) примем, что он должен быть равен 1. Тогда имеем: ху–1=1 → ху=2. Поскольку х и у это цифры, то их значения могут быть равными только 1 и 2 (т.к. только произведение этих однозначных натур.чисел дает в результате 2).

Отсюда z составляет: z=(1+2+1)/(1·2–1)=4/1=4.

Итак, имеем цифры: 1, 2, 4.

Т.к. по условию итоговое число должно быть четным, то оканчиваться оно может только 2 или 4. Тогда правильными вариантами чисел будут такие:

124, 142, 214, 412.

Ответ: 124, 142, 214, 412

---

Вариант 19МБ8

[su_note note_color=”#defae6″]

Найдите шестизначное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Если число делится на 24, значит, оно делится на 8 и на 3.
2. Согласно признаку делимости на 8, 3 последних цифры его должны образовывать число, которое кратно 8.
3. Чтобы число делилось на 3, необходимо, чтобы сумма его цифр делилась на 3. Учитывая уже сформированную 2-ю часть числа (см.п.2), дополняем его первыми тремя цифрами соответственно.

Решение:

Чтобы искомое число было кратно 24, требуется, чтобы оно делилось на 8 и в то же время на 3.

Число делится на 8, если последние его 3 цифры образуют число, кратное 8. С использованием только двоек и нулей такое трехзначное число можно образовать так: 000, 002, 020, 022, 200, 202, 220, 222. Из этих чисел на 8 делится только 000 и 200.

Теперь нужно дополнить искомое число первыми 3-мя цифрами так, чтобы оно делилось еще и на 3.

В 1-м случае это будет единственный вариант: 222000.

Во 2-м случае вариантов два: 220200, 202200.

Ответ: 222000, 220200, 202200

---

Вариант 19МБ9

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 15, произведение цифр которого больше 35, но меньше 45. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Если число кратно 15, значит, оно кратно 3 и 5.
2. Применяем признак делимости на 5 и условие задачи, согласно которому произведение цифр числа ≠0. Так получаем, что последняя цифра искомого числа – только 5.
3. Делим 35 на 5 и 45 на 5. Узнаем диапазон значений, которые может принимать произведение первых 3-х цифр числа. Узнаем, что оно может быть равно только 8.
4. Определяем последовательности цифр, которые дают при перемножении 8.
5. Проверяем полученные из найденных цифр числа на кратность трем.

Решение:

Кратность искомого числа 15 дает 2 условия: оно должно делиться на 5 и на 3.

Если число кратно 5, то оно должно оканчиваться цифрой 5 или 0. Однако 0 в данном случае использовать нельзя, поскольку при этом произведение цифр числа оказывается равным 0. По условию же это не так. Итак, последняя – 4-я – цифра числа равна 5.

По условию 35 < x·5 < 45, где х – произведение первых 3-х цифр числа. Тогда имеем: 7 < x < 9. Это неравенство верно только при х=8. Следовательно, для первых 3-х цифр должны выполняться равенства:

1·1·8=8, 1·2·4=8.

Отсюда получаем числа:

1185; 1245.

Проверяем их на кратность 3:

1+1+8+5=15;

1+2+4+5=12.

Вывод: оба найденные числа кратны 3. Плюс кратны их комбинации:

1815; 8115; 1425; 2145; 2415; 4125; 4215.

Ответ: 1815; 8115; 1425; 2145; 2415; 4125; 4215

---

Вариант 19МБ10

[su_note note_color=”#defae6″]

Найдите пятизначные число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Принимаем во внимание, что на 25 делятся числа, которые придется последовательно делить на 5 дважды. Определяем, какой парой цифр они должны оканчиваться.
2. Учитывая, что 2-й частью условия является различие каждой соседней пары цифр исключительно на 2 единицы, выбираем подходящий вариант (или варианты) цифр.
3. Способом подбора находим остальные цифры и, соответственно, числа. Одно из них запишем в ответе.

Решение:

Если число делится на 25, то оно должно оканчиваться на: 00, 25, 50, 75. Т.к. соседние цифры должны отличаться строго на 2, то использовать для 4-й и 5-й цифр можем только 75. Получаем: ***75.

Далее ищем 3-ю цифру:

1. **975 или
2. **575.

Дальше получаем по аналогии:

1) *7975 → 97975 или 57975;

2) *3575 → 13575 или 53575, *7575 → 57575 или 97575.

Ответ: 97975, 57975, 13575, 53575, 57575, 97575

---

Вариант 19МБ11

[su_note note_color=”#defae6″]

Найдите трехзначное натуральное число, большее 600, которое при делении на 3, на 4 и на 5 дает в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь такое число.

[/su_note]

Алгоритм выполнения

1. Определяем диапазон значений для 1-й цифры числа (сотен).
2. Определяем, какой может быть последняя цифра (единицы), приняв во внимание: 1) при делении на 5 дает в остатке 1; 2) на этом месте не может быть четная цифра, поскольку это одно из условий делимости на 4.
3. Способом подбора определяем набор чисел, которые при делении на 3 дают в остатке 1.
4. Из этого набора (см.п.3) отбрасываем числа, которые при делении на 4 дают остаток, отличный от 1.

Решение:

Т.к. искомое число >600 и при этом является трехзначным, то 1-й цифрой может быть только 6, 7, 8 или 9. Тогда получаем для искомого числа:

6***

7***

8***

9***

Если число при делении на 5 должно давать в остатке 1, значит, оно может оканчиваться только на 0+1=1 или на 5+1=6. Шестерку тут отбрасываем, поскольку в этом случае число четное и потенциально может делиться на 4. Поэтому имеем:

6**1

7**1

8**1

9**1

Если число при делении на 3 дает в остатке 1, значит, сумма его цифр должна быть кратной 3 плюс 1. Кроме того, учитываем, что цифры должны располагаться в числе в порядке убывания. Подбираем такие числа:

631

721

751

841

871

931

961

Из этой последовательности отбрасываем числа, для которых не выполняется условие о том, что число при делении на 4 должно давать в остатке 1.

Т.к. признак делимости на 4 заключается в том, что 2 последние цифры должны делиться на 4, то получаем:

для 631: 31=28+3, т.е. в остатке имеем 3; число не подходит

для 721: 21=20+1, т.е. в остатке – 1; число подходит

для 751: 51=48+3, т.е. в остатке – 3; число не подходит

для 841: 41=40+1, т.е. в остатке – 1; число подходит

для 871: 71=68+3, т.е. в остатке – 3; число не подходит

для 931: 31=28+3, т.е. в остатке – 3; число не подходит

для 961: 61=60+1, т.е. в остатке – 1; число подходит

Ответ:  721, 841, 961

---

Вариант 19МБ12

[su_note note_color=”#defae6″]

Найдите трехзначное натуральное число, большее 400, но меньшее 650, которое делится на каждую свою цифру и все цифры которого различны и не равны 0. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Из условия следует, что числа могут начинаться только на 4,5 или 6.
2. При анализе чисел 4-й сотни отбрасываем числа: 1) 1-го десятка, т.к. в них содержится 0; 2) 4-го десятка, т.к. в этом случае первые две цифры совпадут; 3) числа 5-го десятка, т.к. они должны оканчиваться только на 5 или 0, что недопустимо. Кроме того, для всех четных десятков можно рассматривать только четные числа.
3. Числа 5-й сотни отбрасываем полностью, т.к. чтобы делиться на каждую свою цифру, они должны оканчиваться 5 или 0.
4. Для чисел 6-й сотни рассматривать можно только: 1) четные; 2) кратные 3; 3) не оканчивающиеся 0.

Решение:

Числа 40* и 4*0 отбрасываем, т.к. они содержат 0.

Числа 41* годятся только четные, т.к. это обязательное условия для кратности 4. Анализируем:

412 – подходит

414 – не подходит, т.к. в нем совпадают цифры

416 – не подходит, т.к. не делится на 6

418 – не подходит, т.к. не делится ни на 4, ни на 8

Из чисел 42* годятся только четные, поскольку должны делиться на 2:

422 и 424 – не подходят, т.к. в них совпадают цифры

426 – не подходит, т.к. не делится на 4

428 – не подходит, т.к. не делится на 8

Числа 43* годятся только четные и кратные 3. Поэтому тут подходит только 432.

Числа 44* не подходят полностью.

Числа 45* не подходят полностью, т.к. они должны оканчиваться только 5 (т.е. быть нечетными) или 0.

Числа 46*, 47*, 48*, 49* не подходят полностью, т.к. для каждого из них не выполняется 1 или несколько условий.

Числа 5-й сотни не годятся полностью. Они должны делиться на 5, а для этого оканчиваться либо 5, либо 0, что не допускается.

Числа 60* не годятся полностью.

Среди остальных можно рассматривать только четные, кратные 3, не оканчивающиеся 0. Опуская подробности перебора чисел, оговорим только, что из них годятся: 612, 624, 648. Для остальных не выполняется одно или несколько условий.

Ответ: 412, 432, 612, 624, 648

---

Вариант 19МБ13

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 45, все цифры которого различны и четны. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

1. Если число кратно 45, значит, оно делится на 5 и на 9.
2. Рассматривать следует только числа четных сотен.
3. Оканчиваться числа могут только 0, т.к. 5 – нечетная цифра.
4. Сумма цифр числа должна быть равна 18. Только в этом случае можно составить его из всех четных цифр.

Решение:

Т.к. по условию цифры должны быть четными, то рассматривать можно только числа 2-й, 4-й, 6-й и 8-й тысяч. Это значит, что начинаться оно может с 2, 4, 6 или 8.

Если число кратно 45, то оно кратно 5 и кратно 9.

Если число кратно 5, то оно должно оканчиваться 5 или 0. Но поскольку все цифры должны быть четными, то подходит здесь только 0.

Т.о., получаем шаблоны чисел: 2**0, 4**0, 6**0, 8**0. Отсюда следует, что для проверки кратности 9 требуется, чтобы сумма первых 3-х цифр была равной 9, или 18, или 27 и т.д. Но подходит тут только 18. Основания: 1) для получения в сумме 9 нужно, чтобы одно из слагаемых было нечетным, а это противоречит условию; 2) 27 не подходит потому, что даже если взять самую большую 1-ю цифру 8, то сумма 2-й и 3-й цифр будет равна 27–8=19, что превышает допустимый предел. Еще большие суммы цифр, кратные 9, не подходят тем более.

Рассматриваем числа по тысячам.

Числа 2**0. Сумма средних цифр равна: 18–2=16. Получить 16 из четных чисел можно только так: 8+8. Однако цифры не должны повторяться. Поэтому подходящих условию чисел здесь нет.

Числа 4**0. Сумма средних цифр: 18–4=14. 14=8+6. Поэтому получаем: 4680 или 4860.

Числа 6**0. Сумма средних цифр: 18–6=12. 12=6+6, что не подходит, т.к. цифры повторяются. 12=4+8. Получаем: 6480 или 6840.

Числа 8**0. Сумма средних цифр: 18–8=10. 10=2+8, что не подходит, т.к. при этом будет повторяться 8. 10=4+6. Получаем: 8460 или 8640.

Ответ: 4680, 4860, 6480, 6840, 8460, 8640

Даниил Романович | Просмотров: 12.3k

20
Янв 2017

База ЕГЭ Задание 19

Для вас другие записи этой рубрики:

Овечкинская

СОШ филиал МКОУ «Гоноховская СОШ Завьяловского района »

ЕГЭ по математике.

Задание № 19

Выполнила: Богданова Ольга Николаевна, учитель математики

№ 19

Найдите наименьшее трёхзначное число, которое при делении на 2 даёт остаток 1, при делении на 3 даёт остаток 2, при делении на 5 даёт остаток 3, и которое записано тремя различными нечётными цифрами.

Решение:

Так как число наименьшее, то первая цифра 1.

Так как при делении на 5 даёт остаток 3, то на конце может быть 3 или 8. Но 8 не подходит, так как цифры должны быть нечетные.

Число делится на 3, если сумма его цифр делится на 3. Чтобы получился остаток 2, нужно чтобы сумма цифр результирующего числа была больше той, что делится на 3 ровно на 2.

Ответ: 143

№ 19

Найдите четырёхзначное натуральное число, меньшее 1360, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.

Решение:

По признакам делимости : на 1, на 2, на 3, на 4 и т.д.

Так как число меньшее 1360, то 1 будет первая цифра.

Чтобы число делилось на 2, на конце будет четная цифра.

Чтобы число делилось на 4, на конце будет число, образованное двумя цифрами, которое делится на 4, например, 36.

Чтобы делилось на 3 добавим вторую цифру так, чтобы сумма цифр делилась на 3, например, 2

Проверим, число делится на 6.

Ответ: 1236

№ 19

Найдите наименьшее четырёхзначное число, кратное 11, у которого произведение его цифр равно 12.

Решение:

Разложим число 12 на множители таким образом, чтобы их было ровно 4 (так как четырехзначное) и все они были цифрами:

12 = 6 ⋅ 2 ⋅ 1 ⋅ 1 = 4 ⋅ 3 ⋅ 1 ⋅ 1 = 3 ⋅ 2 ⋅ 2 ⋅ 1

Чтобы число делилось на 11, нужно чтобы сумма цифр, стоящих на четных местах, была равна сумме цифр, стоящих на нечетных местах, или отличалась на 11 . Попробуем разбить каждый из наборов на 2 группы цифр (по 2 цифры в каждом), чтобы они соответствовали условию кратности: первые два набора нельзя так разбить, остается только третий 3 ⋅ 2 ⋅ 2 ⋅ 1. Составляем по признаку число 1232.

Ответ: 1232

№ 19

Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.

Решение:

Например, если сумма цифр равна 7, то произведение должно быть равно 6 (или сумма 5, произведение 4)

Это выполнено для чисел, записываемых тройкой, двойкой и двумя единицами, т.е. 3211, 2311, 1123, 1132, 1213, 1312.

Проверяем делмость на 19

Поскольку число 3211 кратно 19, оно и является искомым.

Ответ: 3211

№ 19

Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого больше 40, но меньше 45. В ответе укажите ровно одно такое число.

Решение:

Так как произведение цифр больше 40, но меньше 45, то оно может быть 41, 42, 43, 44.

Нам подходит только 42 = 6 · 7, те. 1,1 ,6,7

Число кратное 12, то последняя цифра четна, т.е. 6, получим 1,1,7,6

Составляем из этих цифр числа и проверяем их делимость на 12

Ответ: 1176

1716, 7116, 1176

Найдите наименьшее пятизначное число, кратное 55, произведение цифр которого больше 50, но меньше 75. В ответе укажите ровно одно такое число.

№ 19

Решение:

Так как произведение цифр больше 50, но меньше 75, то оно может быть 51, 52, 53, 54….74

Так как число делится на 55, то нам подходит только 55, 60, 65,70

Разложим на простые множители: 55 = 5 · 11, 60 = 15 · 4= 5 · 3 · 2· 2 , 65 = 13 · 5, 70 = 14 · 5 = 2 · 7 ·5

Так как число наименьшее, то нам подходит 70 и оно пятизначное, добавим две 1.

Число кратное 55, то последняя цифра 5, получим 1,1,2,7,5. Составляем из этих цифр числа и проверяем их делимость на 55

Ответ: 11275

Решение:

Так как произведение цифр больше 40, но меньше 45, то оно может быть 41, 42, 43, 44.

Нам подходит только 42 = 6 · 7, те. 1,1 ,6,7

Число кратное 12, то последняя цифра четна, т.е. 6, получим 1,1,7,6

Составляем из этих цифр числа и проверяем его делимость на 12

Ответ: 1176

1716, 7116, 1176

№ 19

Решение:

Так как число больше 300, но меньше 350, то первая цифра числа 3. Так как прибавляем 2, то на конце должен быть в сумме ноль, значит, последняя цифра 8, т.е число 3 . 8

Находим сумму цифр, чтобы делилась на 7, это цифра 3 (3+3+8=14), т.е. 338

Проверяем все условия: 3+3+8 = 14 делится на 7

338 + 2 = 340 (3+4+0=7), 7 делится на 7

Число 338 больше 300 и меньше 350

Ответ: 338

Решение:

Так как число меньше 3000, то первая цифра числа 2 или 1. Пусть будет сначала 2. Так как прибавляем 2, то на конце должен быть в сумме ноль, значит, последняя цифра 8, т.е число 2 . . 8

Находим сумму цифр, чтобы делилась на 8, это цифра 2 и 4, т.е. 2248 или 2428

Проверяем все условия: 2+2+4+8 = 16 делится на 8

2248+2=2250 или 2428 + 2 = 2430, сумма цифр 8, не делится на 7, значит первая цифра будет не 2, а 1, получим 1248 или 1428. Проверим: 1248+2=1250 и 1428+2=1430

Число меньше 3000

Ответ: 1250 или 1430

Найдите трёхзначное число  A , обладающее всеми следующими свойствами:

  · сумма цифр числа  A  делится на 8;

  · сумма цифр числа  A  + 1 делится на 8;

  · в числе  A  сумма крайних цифр кратна средней цифре.

В ответе укажите какое-нибудь одно такое число.

№ 19

Решение:

Так как прибавляем 1, то на конце должен быть в сумме ноль, значит, последняя цифра 9, т.е число . . 9

Находим сумму цифр, чтобы делилась на 8, это цифра 5 и 2, т.е. 529 или 259

Проверяем все условия:

529+1=530 или 259 + 1 = 260, сумма цифр 8, делится на 8, значит первая цифра

В числе  сумма крайних цифр кратна средней цифре: 529 (5+9=14, 14 кратно2)

259 (2+9=11, 11 не кратно 5), значит это число 529

Ответ: 529

№ 19

Сумма цифр трёхзначного числа  A  делится на 13. Сумма цифр числа A +5 также делится на 13. Найдите такое число  A .

Решение:

Так как сумма цифр числа делится на 13, то цифры могут быть: 1,5,7 (сумма цифр 13) или 8,9,9 (сумма цифр 26) и т.д.

Составляем числа и проверяем условия: 1,5,7 не подходят.

А вот 8,9,9. подходят: 899 + 5 = 904 (сумма цифр равнв 13, 13 делится на 13)

Ответ: 899

№ 19

Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.

Решение:

Четные цифры: 0,2,4,6,8

Число кратное 88, значит оно делится на 2,4,8,11

Используем признаки делимости на 4 и 11. Составим такие числа: 2 6 8 4, 2 0 6 8

2 8 6 0, 2640,6248, 8624

Ответ: 2640

Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.

№ 19

Решение:

Так как число делится на 12, то оно делится на 4, на 3.

Так как число делится на 4, то оно четно, т.е на конце число ,образованное двумя цифрами делится на 4, т.е. последнюю 1 вычеркиваем, на конце 12

181615 12

Еще надо вычеркнуть две цифры. Число делится на 3, то сумма цифр делится на 3. Найдем сумму цифр 181615 (22). Надо убрать 1, или 4, или 7, или 10

Надо вычеркнуть две цифры. 1 мало, 4 не получается. Можно убрать 7

(6 и 1), получим 1811512, и др

Ответ: 1811512

Приведите пример шестизначного натурального числа, которое записывается только цифрами 1 и 2 и делится на 24. В ответе укажите ровно одно такое число.

№ 19

Решение:

Так как число делится на 24, то оно делится на 4, на 2 и 3

Так как число делится на 2, то оно четно, на 4 — на конце число, образованное двумя цифрами делится на 4, т.е, на конце . . . . 12

Число делится на 3, то сумма цифр делится на 3. Составляем такие числа:

1221 12 , 2121 12 , 2211 12

Ответ: 122112