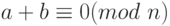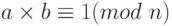Инверсии
Когда мы работаем в модульной арифметике, нам часто нужно найти операцию, которая позволяет вычислить величину, обратную заданному числу. Мы обычно ищем аддитивную инверсию (оператор, обратный сложению) или мультипликативную инверсию (оператор, обратный умножению).
Аддитивная инверсия
В Zn два числа a и b аддитивно инверсны друг другу, если b = n – a. Например,
В Zn аддитивная инверсия числу a может быть вычислена как b = n – a. Например, аддитивная инверсия 4 в Z10 равна 10 – 4 = 6.
В модульной арифметике каждое целое число имеет аддитивную инверсию. Сумма целого числа и его аддитивной инверсии сравнима с 0 по модулю n .
Обратите внимание, что в модульной арифметике каждое число имеет аддитивную инверсию, и эта инверсия уникальна; каждое число имеет одну и только одну аддитивную инверсию. Однако инверсия числа может быть непосредственно тем же самым числом.
Пример 2.21
Найдите все взаимно обратные пары по сложению в Z10.
Решение
Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, 
, (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4.
Мультипликативная инверсия
В Zn два числа a и b мультипликативно инверсны друг другу, если
Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем 
.
В модульной арифметике целое число может или не может иметь мультипликативную инверсию. Целое число и его мультипликативная инверсия сравнимы с 1 по модулю n .
Может быть доказано, что a имеет мультипликативную инверсию в Zn, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые.
Пример 2.22
Найти мультипликативную инверсию 8 в Z10.
Решение
Мультипликативная инверсия не существует, потому что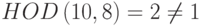 
. Другими словами, мы не можем найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.
Пример 2.23
Найти все мультипликативные инверсии в Z10.
Решение
Есть только три пары, удовлетворяющие условиям существования мультипликативной инверсии: (1, 1), (3, 7) и (9, 9). Числа 0, 2, 4, 5, 6 и 8 не имеют мультипликативной инверсии.
Мы можем проверить, что
(1 x 1) mod 10 = 1 (3 x 7) mod 10 = 1 (9 x 9) mod 10 = 1
Пример 2.24
Найти все мультипликативные обратные пары в Z11.
Решение
Мы имеем следующие пары: (1, 1), (2, 6), (3, 4), (5, 9), (7, и (10, 10). При переходе от Z10 к Z11 число пар увеличивается. При Z11 НОД (11, a) = 1 (взаимно простые) для всех значений a, кроме 0. Это означает, что все целые числа от 1 до 10 имеют мультипликативные инверсии.
Целое число a в Zn имеет мультипликативную инверсию тогда и только тогда, если НОД (n, a) = 1(mod n)
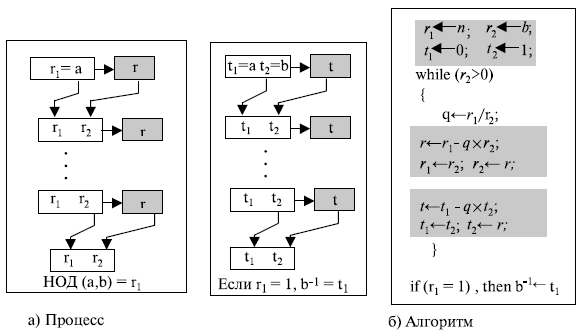
Расширенный алгоритм Евклида, который мы обсуждали ранее в этой лекции, может найти мультипликативную инверсию b в Zn, когда даны n и b и инверсия существует. Для этого нам надо заменить первое целое число a на n (модуль). Далее мы можем утверждать, что алгоритм может найти s и t, такие, что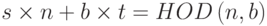 
. Однако если мультипликативная инверсия b существует, НОД (n, b) должен быть 1. Так что уравнение будет иметь вид
(s x n) + (b x t) = 1
Теперь мы применяем операции по модулю к обеим сторонам уравнения. Другими словами, мы отображаем каждую сторону к Zn. Тогда мы будем иметь
(s x n + b x t) mod n =1 mod n [(s x n) mod n] + [(b x t) mod n] = 1 mod n 0 + [(b x t) mod n ] = 1 (b x t) mod n =1 -> Это означает, что t – это мультипликативная инверсия b в Zn
Обратите внимание, что ![[(s times n)bmod n]](https://intuit.ru/sites/default/files/tex_cache/7e3ed054c02628543298573ecfaa9fd3.png)
на третьей строке — 0, потому что, если мы делим 
, частное — s, а остаток — 0.
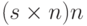
Расширенный алгоритм Евклида находит мультипликативные инверсии b в Zn , когда даны n и b и НОД (n, b) = 1 .
Мультипликативная инверсия b — это значение t , отображенное в Zn .
Рисунок 2.15 показывает, как мы находим мультипликативную инверсию числа, используя расширенный алгоритм Евклида.
Рис.
2.15.
Применение расширенного алгоритма Евклида для поиска мультипликативной инверсии
Пример 2.25
Найти мультипликативную инверсию 11 в Z26.
Решение
Мы используем таблицу, аналогичную одной из тех, которые мы уже применяли прежде при данных r1 = 26 и r2 = 11. Нас интересует только значение t.
| q | r1 | r2 | r | t1 | t2 | t |
|---|---|---|---|---|---|---|
| 2 | 26 | 11 | 4 | 0 | 1 | -2 |
| 2 | 11 | 4 | 3 | 1 | -2 | 5 |
| 1 | 4 | 3 | 1 | -2 | 5 | -7 |
| 3 | 3 | 1 | 0 | 5 | -7 | 26 |
| 1 | 0 | -7 | 26 |
НОД (26, 11) = 1, что означает, что мультипликативная инверсия 11 существует. Расширенный алгоритм Евклида дает t1 = (–7).
Мультипликативная инверсия равна (–7) mod 26 = 19. Другими словами, 11 и 19 — мультипликативная инверсия в Z26. Мы можем видеть, что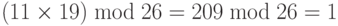 
.
Пример 2.26
Найти мультипликативную инверсию 23 в Z100.
Решение
Мы используем таблицу, подобную той, которую применяли до этого при r1 = 100 и r2 = 23. Нас интересует только значение t.
| q | r1 | r2 | r | t1 | t2 | t |
|---|---|---|---|---|---|---|
| 4 | 100 | 23 | 8 | 0 | 1 | -4 |
| 2 | 23 | 8 | 7 | 1 | -4 | 19 |
| 1 | 8 | 7 | 1 | -4 | 9 | -13 |
| 7 | 7 | 1 | 0 | 9 | -13 | 100 |
| 1 | 0 | -13 | 100 |
НОД (100, 23) = 1, что означает, что инверсия 23 существует. Расширенный Евклидов алгоритм дает t1 =-13. Инверсия — (–13) mod 100 = 87. Другими словами, 13 и 87 — мультипликативные инверсии в Z100. Мы можем видеть, что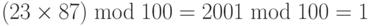 
.
Пример 2.27
Найти мультипликативную инверсию 12 в Z26.
Решение
Мы используем таблицу, подобную той, которую мы применяли раньше при r1 = 26 и r2 = 12.
| q | r1 | r2 | r | t1 | t2 | t |
|---|---|---|---|---|---|---|
| 2 | 26 | 12 | 2 | 0 | 1 | |
| 6 | 12 | 2 | 0 | 1 | -2 | |
| 2 | 0 | -2 | 13 |
, что означает отсутвствие для числа 12 мультипликативной инверсии в Z26
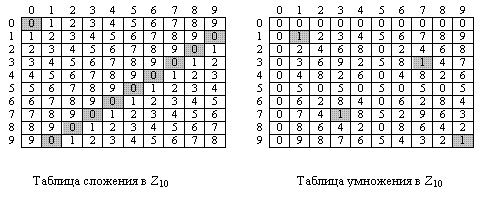
Сложение и умножение таблиц
Рисунок 2.16 показывает две таблицы для сложения и умножения. При сложении таблиц каждое целое число имеет аддитивную инверсию. Обратные пары могут быть найдены, если результат их сложения — ноль. Мы имеем (0, 0), (1, 9), (2, , (3, 7), (4, 6) и (5, 5). При умножении таблиц мы получаем только три мультипликативных пары (1, 1), (3, 7) и (9, 9). Пары могут быть найдены, когда результат умножения равен 1. Обе таблицы симметричны по диагонали, от левой вершины к нижней вершине справа. При этом можно обнаружить свойства коммутативности для сложения и умножения ( a+b = b+a и 
). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.
Рис.
2.16.
Таблицы сложения и умножения для Z10
Различные множества для сложения и умножения
В криптографии мы часто работаем с инверсиями. Если отправитель посылает целое число (например, ключ для шифрования слова), приемник применяет инверсию этого целого числа (например, ключ декодирования). Если это действие (алгоритм шифрования/декодирования) является сложением, множество Zn может быть использовано как множество возможных ключей, потому что каждое целое число в этом множестве имеет аддитивную инверсию. С другой стороны, если действие (алгоритм шифрования/декодирования) — умножение, Zn не может быть множеством возможных ключей, потому что только некоторые члены этого множества имеют мультипликативную инверсию. Нам нужно другое множество, которое является подмножеством Zn и включает в себя только целые числа, и при этом в Zn они имеют уникальную мультипликативную инверсию. Это множество обозначается Zn*. Рисунок 2.17 показывает некоторые
случаи двух множеств. Обратите внимание, что множество Zn*
может быть получено из таблицы умножения типа показанной на рис. 2.16.
Каждый член Zn имеет аддитивную инверсию, но только некоторые члены имеют мультипликативную инверсию. Каждый член Zn* имеет мультипликативную инверсию, но только некоторые члены множества имеют аддитивную инверсию.
Мы должны использовать Zn , когда необходимы аддитивные инверсии; мы должны использовать Zn* , когда необходимы мультипликативные инверсии.
Рис.
2.17.
Некоторые множества Zn и Zn*
Еще два множества
Криптография часто использует еще два множества: Zp, и Zp*. Модули в этих двух множествах — простые числа. Простые числа будут обсуждаться в следующих лекциях; пока можно сказать, что простое число имеет только два делителя: целое число 1 и само себя.
Множество Zp — то же самое, что и Zn, за исключением того, что n — простое число. Zp содержит все целые числа от 0 до p – 1. Каждый элемент в Zp имеет аддитивную инверсию; каждый элемент кроме 0 имеет мультипликативную инверсию.
Множество Zp* — то же самое, что Zn*, за исключением того, что Zp* содержит все целые числа от 1 до p – 1. Каждый элемент в Zp имеет аддитивную и мультипликативную инверсии. Zp* очень хороший кандидат, когда мы нуждаемся во множестве, которое поддерживает аддитивную и мультипликативную инверсии.
Ниже показаны два множества, когда p = 13.
Z13 = {0,1,2,3,4,5,6,7,8,9,10,11,12},
Z13* = {1,2,3,4,5,6,7,8,9,10,11,12},
Что такое обратное число?
Как вы помните, если некое число умножить на число, обратное ему, то получится 1. Из основ арифметики мы знаем следующее:
- Числом, обратным к числу A, называется такое число 1/A, что A * 1/A = 1 (то есть, к примеру, для числа 5 обратным будет 1/5).
- У каждого вещественного числа, кроме 0, есть обратное.
- Умножение на число, обратное A, эквивалентно делению на A (то есть, к примеру, 10/5 — это то же, что 10* 1/5).
Что такое обратное число по модулю?
В модульной арифметике нет операции деления, но есть обратные числа.
-
Число, обратное A (mod C), обозначается A^-1.
-
(A * A^-1) ≡ 1 (mod C) , или, что то же самое, (A * A^-1) mod C = 1.
-
Только у чисел, взаимно простых с C (то есть у тех, у которых нет с C общих простых делителей), есть обратные (mod C)
Как найти обратное число по модулю
Самый
простой метод
нахождения обратного числа к A (mod C) выглядит следующим образом:
Шаг 1. Вычисляем A * B mod C для всех B от 0 до C-1.
Шаг 2. Обратным числом для A mod C будет являться такое B, для которого A * B mod C = 1
Обратите внимание, что B mod C может принимать значения от 0 до C-1, поэтому нет смысла проверять числа, бо́льшие чем B.
Пример: A=3, C=7
Шаг 1. Вычисляем A * B mod C для значений B от 0 до C-1
3 * 5 ≡ 15 (mod 7) ≡
1
(mod 7) <—— ОБРАТНОЕ НАЙДЕНО!
3 * 6 ≡ 18 (mod 7) ≡ 4 (mod 7)
Шаг 2. Обратным значением для A mod C является такое B, при котором A * B mod C = 1
5 — это обратное значение для 3 mod 7, поскольку 5*3 mod 7 = 1.
Давайте рассмотрим другой пример, где обратного значения нет.
Пример: A=2, C=6
Шаг 1. Вычисляем A * B mod C для всех B от 0 до C-1**
Шаг 2. Обратным значением для A mod C является такое B, при котором A * B mod C = 1
Таких значений B, при которых A * B mod C = 1, не существует. Следовательно, у числа A нет обратного значения (mod 6).
Всё дело в том, что числа 2 и 6 не являются взаимно простыми (у них есть общий простой делитель 2).
Кажется, что этот метод слишком медленный…
Есть более быстрый способ нахождения обратного значения для A (mod C), который мы и обсудим в следующих статьях, посвящённых расширенному алгоритму Евклида.
Обратный по модулю
❓Инструкция
Калькулятор онлайн для вычисления обратного элемента по модулю в кольце. Алгоритм поддерживает работу с большими числами с некоторыми ограничениями.
Использование:
Заполняются два поля — число a и модуль m. Число a — число к которому ищем обратный, m — модуль, по которому ищем.
Калькулятор выдает обратный элемент после нажатия на кнопку «Вычислить».
Если установлена галочка «подробнее», то калькулятор помимо обратного элемента по модулю выдает некоторые этапы вычисления.
Ограничения:
Калькулятор поддерживает работу с большими целыми числами (в том числе отрицательными числами для числа a, и только положительными для модулю m) длиной не более 10 000 символов.
📖 Теория
Что значит по модулю?
Синонимом к данному выражению является выражение «остаток от деления«. То есть выражение «5 по модулю 3» эквивалентно выражению «остаток от деления 5 на 3». И в том и в другом случае подразумевается в ответе число 2, так как остаток от деления 5 на 3 = 2.
Стоить отметить тот факт, что по модулю m мы имеем числа от 0 до m — 1. Действительно, остаток от деления на m никогда не превысит m — 1.
Что такое обратное?
Напомним, что число, умноженное на его обратное, равно 1. Из базовой арифметики мы знаем, что:
Число, обратное к числу A, равно 1 / A, поскольку A * (1 / A) = 1 (например, значение, обратное к 5, равно 1/5). Все действительные числа, кроме 0, имеют обратную Умножение числа на обратное к A эквивалентно делению на A (например, 10/5 соответствует 10 * 1/5)
Что такое обратное по модулю?
В модульной арифметике у нас нет операции деления. Тем не менее, у нас есть модульные инверсии.
Модульная инверсия a (mod m) есть a-1 (a * a-1) ≡ 1 (mod m) или эквивалентно (a * a-1) mod m = 1 Только числа, взаимно простые с модулем m, имеют модульное обратное.
Говоря проще, обратным элементом к a по модулю m является такое число b, что остаток от деления (a * b) на модуль m равно единице (a * a-1) mod m = 1
Как найти модульный обратный
Наивный метод нахождения модульного обратного a ( по модулю m) является:
Шаг 1. Рассчитать a * b mod m для значений b от 0 до m — 1
Шаг 2. Модульная инверсия a mod m — это значение b, при котором a * b mod m = 1
Обратите внимание, что термин b mod m может иметь только целочисленное значение от 0 до m — 1, поэтому тестирование больших значений чем (m-1) для b является излишним.
Вы наверно уже догадались, что наивный метод является очень медленным. Перебор всех чисел от 0 до m-1 для большого модуля довольно-таки трудоемкая задача. Существует гораздо более быстрый метод нахождения инверсии a (mod m). Таковым является расширенный алгоритм Евклида, который реализован в данном калькуляторе.
Расширенный алгоритм Евклида
Представим наибольший общий делитель числа a и модуля m в виде ax + my. То есть НОД(a, m) = ax + my. Помним, что обратный элемент существует только тогда, когда a и m взаимно просты, то есть их НОД(a, m) = 1. Отсюда: ax + my = 1 — линейное диофантово уравнение второго порядка. Необходимо решить данное уравнение в целых числах и найти x, y.
Найденный коэффициент x будет являться обратным элементом к a по модулю m. Это следует оттуда, что, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим: ax = 1 (m).
Расширенный алгоритм Евклида, в отличие от классического, помимо наибольшего общего делителя позволяет найти также коэффициенты x, y.
Алгоритм:
Вход: a, m ≠ 0
Выход: d, x, y, такие что d = gcd(a, m) = ax + my
1. [Инициализация] (a0, a1) := (a, m); (x0, x1) := (1, 0); (y0; y1) := (0, 1).
2. [Основной цикл] Пока a1 ≠ 0 выполнять {q = QUO(a0, a1);
(a0, a1) := (a1, a0 — a1q); (x0, x1) := (x1, x0 — x1q); (y0, y1) := (y1, y0 — y1q);
QUO(a0, a1) — целая часть от деления a0 на a1
3. [Выход] Вернуть (d, x, y) = (a0, x0, y0)
Битовая сложность расширенного алгоритма Евклида равна O((log2(n))2) , где n = max (|a|, |m|)
Непонятен алгоритм? Ничего страшного, примеры ниже именно для этого и предназначены.
➕ Примеры
Пример для наивного метода.
Пусть a = 3, m = 7. То есть нам необходимо найти обратный элемент к 3 по модулю 7.
Шаг 1. Рассчитать a * b mod m для значений B от 0 до m-1. По очереди проверяем числа от 0 до 6.
3 * 0 ≡ 0 (mod 7) — не подходит
3 * 1 ≡ 3 (mod 7)
3 * 2 ≡ 6 (mod 7)
3 * 3 ≡ 9 ≡ 2 (mod 7)
3 * 4 ≡ 12 ≡ 5 (mod 7)
3 * 5 ≡ 15 (mod 7) ≡ 1 (mod 7) <—— Обратное найдено.
3 * 6 ≡ 18 (mod 7) ≡ 4 (mod 7)
при b = 5 выполнилось условие, что a * b ≡ 1 (m). Следовательно, b = 5 является обратным элементом к 3 по модулю 7.
Пример на расширенный алгоритм Евклида.
Пусть аналогично предыдущему примеру имеем a = 3, m = 7. Также, требуется найти обратный элемент к 3 по модулю 7. Согласно алгоритму начинаем заполнять таблицу на каждом этапе цикла.
| Итерация | q | a0 | a1 | x0 | x1 | y0 | y1 |
| 0 | — | 3 | 7 | 1 | 0 | 0 | 1 |
| 1 | 0 | 7 | 3 | 0 | 1 | 1 | 0 |
| 2 | 2 | 3 | 1 | 1 | -2 | 0 | 1 |
| 3 | 3 | 1 | 0 | -2 | 0 | 1 | -3 |
После 3-ей итерации получили a1 = 0, строго по алгоритму из раздела «Теория» заканчиваем работу алгоритма.
(d, x, y) = (a0, x0, y0)
(d, x, y) = (1, -2, 1), видим, что d = НОД(3, 7) = 1, следовательно числа 3 и 7 являются взаимно простыми, а значит обратный существует.
Делаем проверку:
3 * (-2) + 7 * 1 = 1
-6 + 7 = 1
1 = 1 — верно!
Обратным элементом к тройке по модулю 7 является x = -2. По модулю 7 число -2 равно 5. Получили, что x = 5 является обратным элементом к 3 по модулю 7.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Обратный элемент по модулю
Часто в задачах требуется посчитать что-то по простому модулю (чаще всего (10^9 + 7)). Это делают для того, чтобы участникам не приходилось использовать длинную арифметику, и они могли сосредоточиться на самой задаче.
Обычные арифметические операции выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
c = (a + b) % mod;
c = (mod + a - b) % mod;
c = a * b % mod;Но вот с делением возникают проблемы — мы не можем просто взять и поделить. Пример: (frac{8}{2} = 4), но (frac{8 % 5 = 3}{2 % 5 = 2} neq 4).
Нужно найти некоторый элемент, который будет себя вести как (frac{1}{a} = a^{-1}), и вместо «деления» домножать на него. Назовем такой элемент обратным.
Способ 1: бинарное возведение в степень
Если модуль (p) простой, то решением будет (a^{-1} equiv a^{p-2}). Это следует из малой теоремы Ферма:
Теорема. (a^p equiv a pmod p) для всех (a), не делящихся на (p).
Доказательство. (для понимания несущественно, можно пропустить)
[
begin{aligned}
a^p &= (underbrace{1+1+ldots+1+1}_text{$a$ раз})^p
\ &= sum_{x_1+x_2+ldots+x_a = p} P(x_1, x_2, ldots, x_a) & text{(раскладываем по определению)}
\ &= sum_{x_1+x_2+ldots+x_a = p} frac{p!}{x_1! x_2! ldots x_a!} & text{(какие слагаемые не делятся на $p$?)}
\ &equiv P(p, 0, ldots, 0) + ldots + P(0, 0, ldots, p) & text{(все остальные не убьют $p$ в знаменателе)}
\ &= a
end{aligned}
]
Здесь (P(x_1, x_2, ldots, x_n) = frac{k}{prod (x_i!)}) это мультиномиальный коеффициент — количество раз, которое элемент (a_1^{x_1} a_2^{x_2} ldots a_n^{x_n}) появится при раскрытии скобки ((a_1 + a_2 + ldots + a_n)^k).
Теперь два раза «поделим» наш результат на (a).
[ a^p equiv a implies a^{p-1} equiv 1 implies a^{p-2} equiv a^{-1} ]
Получается, что (a^{p-2}) ведет себя как (a^{-1}), что нам по сути и нужно. Посчитать (a^{p-2}) можно за (O(log p)) бинарным возведением в степень.
Приведем код, который позволяет считает (C_n^k).
int t[maxn]; // факториалы, можно предподситать простым циклом
// бинарное возведение в степень
int bp (int a, int n) {
int res = 1;
while (n) {
if (n & 1) res = res * a % mod;
a = a * a % mod;
n >>= 1;
}
return res;
}
// находит обратный элемент как a^(p-2)
int inv (int x) {
return bp(x, mod-2);
}
int c (int n, int k) {
return t[n] * inv(t[k]) % mod * inv(t[n-k]) % mod;
}Способ 2: диофантово уравнение
Диофантовыми уравнениями называют такие штуки:
[ ax + by = 1 ]
Требуется решить их в целых числах, то есть (a) и (b) известны, и нужно найти такие целые (возможно, отрицательные) (x) и (y), чтобы равенство выполнялось. Решают такие вещи расширенным алгоритмом Евклида. TODO: описать, как он работает.
Подставим в качестве (a) и (b) соответственно (a) и (m)
[ ax + my = 1 ]
Одним из решений уравнения и будет (a^{-1}), потому что если взять уравнение по модулю (m), то получим
[ ax + by = 1 iff ax equiv 1 iff x equiv a^{-1} pmod m ]
Преимущества этого метода над возведением в степень:
- Если обратное существует, то оно найдется даже если модуль не простой. Способ с бинарным возведением тоже можно заставить работать с произвольным модулем, но это будет намного труднее.
- Алгоритм проще выполнять руками.
Сам автор почти всегда использует возведение в степень.
Почему (10^9+7)?
- Это выражение довольно легко вбивать (
1e9+7). - Простое число.
- Достаточно большое.
intне переполняется при сложении.long longне переполняется при умножении.
Кстати, (10^9 + 9) обладает теми же свойствами. Иногда используют и его.
Предподсчёт обратных факториалов за линейное время
Пусть нам нужно зачем-то посчитать все те же (C_n^k), но для больших (n) и (k), поэтому асимптотика (O(n log m)) нас не устроит. Оказывается, мы можем сразу предподсчитать все обратные ко всем факториалам.
Если у нас уже написан inv, то нам не жалко потратить (O(log m)) операций, посчитав (m!^{-1}).
После этого мы будем считать ((m-1)!^{-1}) как (m!^{-1} m = frac{1}{1 cdot 2 cdot ldots cdot (m-1)}).
int f[maxn];
f[0] = 1;
for (int i = 1; i < maxn; i++)
f[i] = i*f[i-1] % mod;
int r[maxn];
r[maxn-1] = inv(f[maxn-1])
for (int i = maxn-1; i >= 1; i--)
r[i-1] = r[i]*i % mod;TODO: техника с сайта емакса.