Как найти числа пифагора - Исправление недочетов и поиск решений вместе с Examum.ru

Пифагорово число (пифагорова тройка) — комбинация из трёх целых чисел , удовлетворяющих соотношению Пифагора: ${displaystyle x^{2}+y^{2}=z^{2}}$ .

Свойства

Поскольку уравнение ${displaystyle x^{2}+y^{2}=z^{2}}$ однородно, при домножении , и на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть — взаимно простые числа.

Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, т. е. таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 ( ${displaystyle 3^{2}+4^{2}=5^{2}}$ ).

Пифагорова тройка задаёт точку с рациональными координатами ${displaystyle left({frac {a}{c}},;{frac {b}{c}}right)}$ на единичной окружности ${displaystyle x^{2}+y^{2}=1}$ .

Любая примитивная пифагорова тройка однозначно представляется в виде ${displaystyle (m^{2}-n^{2},;2mn,;m^{2}+n^{2})}$ для некоторых натуральных, взаимно простых , имеющих разную чётность. Наоборот, любая такая пара задаёт примитивную пифагорову тройку.Шаблон:Источник?

Примеры

Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):

(3, 4, 5),
(6, 8, 10),
(5, 12, 13),
(9, 12, 15),
(8, 15, 17),
(12, 16, 20),
(15, 20, 25),
(7, 24, 25),
(10, 24, 26),
(20, 21, 29),
(18, 24, 30),
(16, 30, 34),
(21, 28, 35),
(12, 35, 37),
(15, 36, 39),
(24, 32, 40),
(9, 40, 41),
(14, 48, 50),
(30, 40, 50)…

См. также

Великая теорема Ферма
Теорема Пифагора

be-x-old:Піфагорава тройка
bg:Питагоров триъгълник
da:Pythagoræiske tal
eo:Pitagora triopo
he:שלשה פיתגורית
hu:Pitagoraszi számhármasok
is:Pýþagórískur þríhyrningur
nl:Pythagorese drietallen
pl:Trójki pitagorejskie
scn:Terna pitagòrica
sl:Pitagorejska trojica
sv:Pythagoreisk trippel

Ещё примеры пифагоровых троек (где катеты меньше 1000, их 179):

3 4 5  9+16=25

5 12 13  25+144=169

7 24 25  49+576=625

8 15 17  64+225=289

9 40 41  81+1600=1681

11 60 61  121+3600=3721

12 35 37  144+1225=1369

13 84 85  169+7056=7225

15 112 113  225+12544=12769

16 63 65  256+3969=4225

17 144 145  289+20736=21025

19 180 181  361+32400=32761

20 21 29  400+441=841

20 99 101  400+9801=10201

21 220 221  441+48400=48841

23 264 265  529+69696=70225

24 143 145  576+20449=21025

25 312 313  625+97344=97969

27 364 365  729+132496=133225

28 45 53  784+2025=2809

28 195 197  784+38025=38809

29 420 421  841+176400=177241

31 480 481  961+230400=231361

32 255 257  1024+65025=66049

33 56 65  1089+3136=4225

33 544 545  1089+295936=297025

35 612 613  1225+374544=375769

36 77 85  1296+5929=7225

36 323 325  1296+104329=105625

37 684 685  1369+467856=469225

39 80 89  1521+6400=7921

39 760 761  1521+577600=579121

40 399 401  1600+159201=160801

41 840 841  1681+705600=707281

43 924 925  1849+853776=855625

44 117 125  1936+13689=15625

44 483 485  1936+233289=235225

48 55 73  2304+3025=5329

48 575 577  2304+330625=332929

51 140 149  2601+19600=22201

52 165 173  2704+27225=29929

52 675 677  2704+455625=458329

56 783 785  3136+613089=616225

57 176 185  3249+30976=34225

60 91 109  3600+8281=11881

60 221 229  3600+48841=52441

60 899 901  3600+808201=811801

65 72 97  4225+5184=9409

68 285 293  4624+81225=85849

69 260 269  4761+67600=72361

75 308 317  5625+94864=100489

76 357 365  5776+127449=133225

84 187 205  7056+34969=42025

84 437 445  7056+190969=198025

85 132 157  7225+17424=24649

87 416 425  7569+173056=180625

88 105 137  7744+11025=18769

92 525 533  8464+275625=284089

93 476 485  8649+226576=235225

95 168 193  9025+28224=37249

96 247 265  9216+61009=70225

100 621 629  10000+385641=395641

104 153 185  10816+23409=34225

105 208 233  11025+43264=54289

105 608 617  11025+369664=380689

108 725 733  11664+525625=537289

111 680 689  12321+462400=474721

115 252 277  13225+63504=76729

116 837 845  13456+700569=714025

119 120 169  14161+14400=28561

120 209 241  14400+43681=58081

120 391 409  14400+152881=167281

123 836 845  15129+698896=714025

124 957 965  15376+915849=931225

129 920 929  16641+846400=863041

132 475 493  17424+225625=243049

133 156 205  17689+24336=42025

135 352 377  18225+123904=142129

136 273 305  18496+74529=93025

140 171 221  19600+29241=48841

145 408 433  21025+166464=187489

152 345 377  23104+119025=142129

155 468 493  24025+219024=243049

156 667 685  24336+444889=469225

160 231 281  25600+53361=78961

161 240 289  25921+57600=83521

165 532 557  27225+283024=310249

168 425 457  28224+180625=208849

168 775 793  28224+600625=628849

175 288 337  30625+82944=113569

180 299 349  32400+89401=121801

184 513 545  33856+263169=297025

185 672 697  34225+451584=485809

189 340 389  35721+115600=151321

195 748 773  38025+559504=597529

200 609 641  40000+370881=410881

203 396 445  41209+156816=198025

204 253 325  41616+64009=105625

205 828 853  42025+685584=727609

207 224 305  42849+50176=93025

215 912 937  46225+831744=877969

216 713 745  46656+508369=555025

217 456 505  47089+207936=255025

220 459 509  48400+210681=259081

225 272 353  50625+73984=124609

228 325 397  51984+105625=157609

231 520 569  53361+270400=323761

232 825 857  53824+680625=734449

240 551 601  57600+303601=361201

248 945 977  61504+893025=954529

252 275 373  63504+75625=139129

259 660 709  67081+435600=502681

260 651 701  67600+423801=491401

261 380 461  68121+144400=212521

273 736 785  74529+541696=616225

276 493 565  76176+243049=319225

279 440 521  77841+193600=271441

280 351 449  78400+123201=201601

280 759 809  78400+576081=654481

287 816 865  82369+665856=748225

297 304 425  88209+92416=180625

300 589 661  90000+346921=436921

301 900 949  90601+810000=900601

308 435 533  94864+189225=284089

315 572 653  99225+327184=426409

315 988 1037  99225+976144=1075369

319 360 481  101761+129600=231361

320 999 1049  102400+998001=1100401

333 644 725  110889+414736=525625

336 377 505  112896+142129=255025

336 527 625  112896+277729=390625

341 420 541  116281+176400=292681

348 805 877  121104+648025=769129

364 627 725  132496+393129=525625

368 465 593  135424+216225=351649

369 800 881  136161+640000=776161

372 925 997  138384+855625=994009

385 552 673  148225+304704=452929

387 884 965  149769+781456=931225

396 403 565  156816+162409=319225

400 561 689  160000+314721=474721

407 624 745  165649+389376=555025

420 851 949  176400+724201=900601

429 460 629  184041+211600=395641

429 700 821  184041+490000=674041

432 665 793  186624+442225=628849

448 975 1073  200704+950625=1151329

451 780 901  203401+608400=811801

455 528 697  207025+278784=485809

464 777 905  215296+603729=819025

468 595 757  219024+354025=573049

473 864 985  223729+746496=970225

481 600 769  231361+360000=591361

495 952 1073  245025+906304=1151329

496 897 1025  246016+804609=1050625

504 703 865  254016+494209=748225

533 756 925  284089+571536=855625

540 629 829  291600+395641=687241

555 572 797  308025+327184=635209

559 840 1009  312481+705600=1018081

576 943 1105  331776+889249=1221025

580 741 941  336400+549081=885481

585 928 1097  342225+861184=1203409

615 728 953  378225+529984=908209

616 663 905  379456+439569=819025

620 861 1061  384400+741321=1125721

645 812 1037  416025+659344=1075369

660 779 1021  435600+606841=1042441

660 989 1189  435600+978121=1413721

696 697 985  484416+485809=970225

704 903 1145  495616+815409=1311025

705 992 1217  497025+984064=1481089

731 780 1069  534361+608400=1142761

744 817 1105  553536+667489=1221025

765 868 1157  585225+753424=1338649

799 960 1249  638401+921600=1560001

832 855 1193  692224+731025=1423249

884 987 1325  781456+974169=1755625

893 924 1285  797449+853776=1651225

Ссылки

Пифагоровы тройки чисел — Yaptro

Источник

Besides Euclid’s formula, many other formulas for generating Pythagorean triples have been developed.

Euclid’s, Pythagoras’, and Plato’s formulas[edit]

Euclid’s, Pythagoras’ and Plato’s formulas for calculating triples have been described here:

The methods below appear in various sources, often without attribution as to their origin.

Fibonacci’s method[edit]

Leonardo of Pisa (c. 1170 – c. 1250) described this method^[1]^[2] for generating primitive triples using the sequence of consecutive odd integers and the fact that the sum of the first terms of this sequence is $n^{2}$ . If is the -th member of this sequence then .

Choose any odd square number from this sequence ( $k=a^{2}$ ) and let this square be the -th term of the sequence. Also, let $b^{2}$ be the sum of the previous n-1 terms, and let $c^{2}$ be the sum of all terms. Then we have established that $a^{2}+b^{2}=c^{2}$ and we have generated the primitive triple [a, b, c]. This method produces an infinite number of primitive triples, but not all of them.

EXAMPLE:
Choose $k=9=3^{2}=a^{2}$ . This odd square number is the fifth term of the sequence, because $5=n=(a^{2}+1)/2$ . The sum of the previous 4 terms is $b^{2}=4^{2}$ and the sum of all n=5 terms is $c^{2}=5^{2}$ giving us $a^{2}+b^{2}=c^{2}$ and the primitive triple [a, b, c] = [3, 4, 5].

Sequences of mixed numbers[edit]

Michael Stifel published the following method in 1544.^[3]^[4] Consider the sequence of mixed numbers ${displaystyle 1{tfrac {1}{3}},,2{tfrac {2}{5}},,3{tfrac {3}{7}},,4{tfrac {4}{9}},,ldots }$ with ${displaystyle a_{n}=n+{tfrac {n}{2n+1}}}$ . To calculate a Pythagorean triple, take any term of this sequence and convert it to an improper fraction (for mixed number ${displaystyle 1{tfrac {1}{3}}}$ , the corresponding improper fraction is $tfrac{4}{3}$ ). Then its numerator and denominator are the sides, b and a, of a right triangle, and the hypotenuse is b + 1. For example:

${displaystyle 1{tfrac {1}{3}}rightarrow [3,4,5],;2{tfrac {2}{5}}rightarrow [5,12,13],;3{tfrac {3}{7}}rightarrow [7,24,25],;4{tfrac {4}{9}}rightarrow [9,40,41],;ldots }$

Jacques Ozanam^[5] republished Stifel’s sequence in 1694 and added the similar sequence ${displaystyle 1{tfrac {7}{8}},,2{tfrac {11}{12}},,3{tfrac {15}{16}},,4{tfrac {19}{20}},,ldots }$ with ${displaystyle a_{n}=n+{tfrac {4n+3}{4n+4}}}$ . As before, to produce a triple from this sequence, take any term and convert it to an improper fraction. Then its numerator and denominator are the sides, b and a, of a right triangle, and the hypotenuse is b + 2. For example:

${displaystyle 1{tfrac {7}{8}}rightarrow [8,15,17],;2{tfrac {11}{12}}rightarrow [12,35,37],;3{tfrac {15}{16}}rightarrow [16,63,65],;4{tfrac {19}{20}}rightarrow [20,99,101],;ldots }$

With a the shorter and b the longer legs of a triangle and c its hypotenuse, the Pythagoras family of triplets is defined by c − b = 1, the Plato family by c − b = 2, and the Fermat family by |a − b| = 1. The Stifel sequence produces all primitive triplets of the Pythagoras family, and the Ozanam sequence produces all primitive triples of the Plato family. The triplets of the Fermat family must be found by other means.

Dickson’s method[edit]

Leonard Eugene Dickson (1920)^[6] attributes to himself the following method for generating Pythagorean triples. To find integer solutions to $x^{2}+y^{2}=z^{2}$ , find positive integers r, s, and t such that $r^{2}=2st$ is a perfect square.

Then:

From this we see that is any even integer and that s and t are factors of ${tfrac {r^{2}}{2}}$ . All Pythagorean triples may be found by this method. When s and t are coprime, the triple will be primitive. A simple proof of Dickson’s method has been presented by Josef Rukavicka, J. (2013).^[7]

Example: Choose r = 6. Then ${tfrac {r^{2}}{2}}=18$ .
The three factor-pairs of 18 are: (1, 18), (2, 9), and (3, 6). All three factor pairs will produce triples using the above equations.

s = 1, t = 18 produces the triple [7, 24, 25] because x = 6 + 1 = 7, y = 6 + 18 = 24, z = 6 + 1 + 18 = 25.

s = 2, t = 9 produces the triple [8, 15, 17] because x = 6 + 2 = 8, y = 6 + 9 = 15, z = 6 + 2 + 9 = 17.

s = 3, t = 6 produces the triple [9, 12, 15] because x = 6 + 3 = 9, y = 6 + 6 = 12, z = 6 + 3 + 6 = 15. (Since s and t are not coprime, this triple is not primitive.)

Generalized Fibonacci sequence[edit]

Method I[edit]

For Fibonacci numbers starting with F₁ = 0 and F₂ = 1 and with each succeeding Fibonacci number being the sum of the preceding two, one can generate a sequence of Pythagorean triples starting from (a₃, b₃, c₃) = (4, 3, 5) via

$(a_{n},b_{n},c_{n})=(a_{{n-1}}+b_{{n-1}}+c_{{n-1}},,F_{{2n-1}}-b_{{n-1}},,F_{{2n}})$

for n ≥ 4.

Method II[edit]

A Pythagorean triple can be generated using any two positive integers by the following procedures using generalized Fibonacci sequences.

For initial positive integers h_n and h_n+1, if h_n + h_n+1 = h_n+2 and h_n+1 + h_n+2 = h_n+3, then

$(2h_{{n+1}}h_{{n+2}},h_{n}h_{{n+3}},2h_{{n+1}}h_{{n+2}}+h_{n}^{2})$

is a Pythagorean triple.^[8]

Method III[edit]

The following is a matrix-based approach to generating primitive triples with generalized Fibonacci sequences.^[9] Start with a 2 × 2 array and insert two coprime positive integers ( q,q’ ) in the top row. Place the even integer (if any) in the left-hand column.

$left[{{begin{array}{*{20}c}q&{q'}\bullet &bullet end{array}}}right]$

Now apply the following «Fibonacci rule» to get the entries in the bottom
row:

${begin{array}{*{20}c}q'+q=p\q+p=p'end{array}}to left[{{begin{array}{*{20}c}q&q'\p&p'end{array}}}right]$

Such an array may be called a «Fibonacci Box». Note that q’, q, p, p’ is a generalized Fibonacci sequence. Taking column, row, and diagonal products we obtain the sides of triangle [a, b, c], its area A, and its perimeter P, as well as the radii r_i of its incircle and three excircles as follows:

${displaystyle {begin{array}{l}a=2qp\b=q'p'\c=pp'-qq'=qp'+q'p\\{text{radii}}to (r_{1}=qq',r_{2}=qp',r_{3}=q'p,r_{4}=pp')\A=qq'pp'\P=r_{1}+r_{2}+r_{3}+r_{4}end{array}}}$

The half-angle tangents at the acute angles are q/p and q’/p’.

EXAMPLE:

Using coprime integers 9 and 2.

$left[{{begin{array}{*{20}c}2&9\bullet &bullet end{array}}}right]to left[{{begin{array}{*{20}c}2&9\11&13end{array}}}right]$

The column, row, and diagonal products are: (columns: 22 and 117), (rows: 18 and 143), (diagonals: 26 and 99), so

${displaystyle {begin{array}{l}a=2(22)=44\b=117\c=(143-18)=(26+99)=125\\{text{radii}}to (r_{1}=18,quad r_{2}=26,quad r_{3}=99,quad r_{4}=143)\A=18(143)=2574\P=(18+26+99+143)=286end{array}}}$

The half-angle tangents at the acute angles are 2/11 and 9/13. Note that if the chosen integers q, q’ are not coprime, the same procedure leads to a non-primitive triple.

Pythagorean triples and Descartes’ circle equation[edit]

This method of generating primitive Pythagorean triples also provides integer solutions to Descartes’ Circle Equation,^[9]

$left(k_{1}+k_{2}+k_{3}+k_{4}right)^{2}=2left(k_{1}^{2}+k_{2}^{2}+k_{3}^{2}+k_{4}^{2}right),$

where integer curvatures k_i are obtained by multiplying the reciprocal of each radius by the area A. The result is k₁ = pp’, k₂ = qp’, k₃ = q’p, k₄ = qq’. Here, the largest circle is taken as having negative curvature with respect to the other three. The largest circle (curvature k₄) may also be replaced by a smaller circle with positive curvature ( k₀ = 4pp’ − qq’ ).

EXAMPLE:

Using the area and four radii obtained above for primitive triple [44, 117, 125] we obtain the following integer solutions to Descartes’ Equation: k₁ = 143, k₂ = 99, k₃ = 26, k₄ = (−18), and k₀ = 554.

A Ternary Tree: Generating All Primitive Pythagorean Triples[edit]

Each primitive Pythagorean triple corresponds uniquely to a Fibonacci Box. Conversely, each Fibonacci Box corresponds to a unique and primitive Pythagorean triple. In this section we shall use the Fibonacci Box in place of the primitive triple it represents. An infinite ternary tree containing all primitive Pythagorean triples/Fibonacci Boxes can be constructed by the following procedure.^[10]

Consider a Fibonacci Box containing two, odd, coprime integers x and y in the right-hand column.

$left[{{begin{array}{*{20}{c}}bullet &x\bullet &yend{array}}}right]$

It may be seen that these integers can also be placed as follows:

$left[{{begin{array}{*{20}{c}}bullet &x\y&bullet end{array}}}right],left[{{begin{array}{*{20}{c}}x&y\bullet &bullet end{array}}}right],left[{{begin{array}{*{20}{c}}y&x\bullet &bullet end{array}}}right]$

resulting in three more valid Fibonacci boxes containing x and y. We may think of the first Box as the «parent» of the next three. For example, if x = 1 and y = 3 we have:

$left[{{begin{array}{*{20}{c}}1&1\2&3end{array}}}right]leftarrow {text{parent}}$

$left[{{begin{array}{*{20}{c}}2&1\3&5end{array}}}right],left[{{begin{array}{*{20}{c}}1&3\4&5end{array}}}right],left[{{begin{array}{*{20}{c}}3&1\4&7end{array}}}right]leftarrow {text{children}}$

Moreover, each «child» is itself the parent of three more children which can be obtained by the same procedure. Continuing this process at each node leads to an infinite ternary tree containing all possible Fibonacci Boxes, or equivalently, to a ternary tree containing all possible primitive triples. (The tree shown here is distinct from the classic tree described by Berggren in 1934, and has many different number-theoretic properties.) Compare: «Classic Tree».^[11] See also Tree of primitive Pythagorean triples.^[12]

Generating triples using quadratic equations[edit]

There are several methods for defining quadratic equations for calculating each leg of a Pythagorean triple.^[13] A simple method is to modify the standard Euclid equation by adding a variable x to each m and n pair. The m, n pair is treated as a constant while the value of x is varied to produce a «family» of triples based on the selected triple. An arbitrary coefficient can be placed in front of the «x» value on either m or n, which causes the resulting equation to systematically «skip» through the triples. For example, consider the triple [20, 21, 29] which can be calculated from the Euclid equations with a value of m = 5 and n = 2. Also, arbitrarily put the coefficient of 4 in front of the «x» in the «m» term.

Let $m_{1}=(4x+m)$ and let $n_{1}=(x+n)$

Hence, substituting the values of m and n:

${begin{aligned}{text{Side }}A&=2m_{1}n_{1}&&=2(4x+5){text{ }}(x+2)&&=8x^{2}+26x+20\{text{Side }}B&=m_{1}^{2}-n_{1}^{2}&&=(4x+5)^{2}-(x+2)^{2}&&=15x^{2}+36x+21\{text{Side }}C&=m_{1}^{2}+n_{1}^{2}&&=(4x+5)^{2}+(x+2)^{2}&&=17x^{2}+44x+29end{aligned}}$

Note that the original triple comprises the constant term in each of the respective quadratic equations. Below is a sample output from these equations. Note that the effect of these equations is to cause the «m» value in the Euclid equations to increment in steps of 4, while the «n» value increments by 1.

x	side a	side b	side c	m	n
0	20	21	29	5	2
1	54	72	90	9	3
2	104	153	185	13	4
3	170	264	314	17	5
4	252	405	477	21	6

Generating all primitive Pythagorean triples using half-angle tangents[edit]

A primitive Pythagorean triple can be reconstructed from a half-angle tangent. Choose r to be a positive rational number in (0, 1) to be tan(A / 2) for the interior angle A that is opposite the side of length a. Using tangent half-angle formulas, it follows immediately that α = sin(A) = 2r / (1 + r²) and β = cos(A) = (1 − r²) / (1 + r²) are both rational and that α² + β² = 1. Multiplying up by the smallest integer that clears the denominators of α and β recovers the original primitive Pythagorean triple. Note that if a < b is desired then r should be chosen to be less than √2 − 1.

The interior angle B that is opposite the side of length b will be the complementary angle of A. We can calculate s = tan(B / 2) = tan(π/4 − A/2) = (1 — r) / (1 + r) from the formula for the tangent of the difference of angles. Use of s instead of r in the above formulas will give the same primitive Pythagorean triple but with a and b swapped.

Note that r and s can be reconstructed from a, b, and c using r = a / (b + c) and s = b / (a + c).

Pythagorean triples by use of matrices and linear transformations[edit]

Let [a, b, c] be a primitive triple with a odd. Then 3 new triples [a₁, b₁, c₁], [a₂, b₂, c₂], [a₃, b₃, c₃] may be produced from [a, b, c] using matrix multiplication and Berggren’s^[11] three matrices A, B, C. Triple [a, b, c] is termed the parent of the three new triples (the children). Each child is itself the parent of 3 more children, and so on. If one begins with primitive triple [3, 4, 5], all primitive triples will eventually be produced by application of these matrices. The result can be graphically represented as an infinite ternary tree with [a, b, c] at the root node. An equivalent result may be obtained using Berggrens’s three linear transformations shown below.

${overset {A}{{mathop {left[{begin{matrix}-1&2&2\-2&1&2\-2&2&3\end{matrix}}right]}}}}left[{begin{matrix}a\b\c\end{matrix}}right]=left[{begin{matrix}a_{1}\b_{1}\c_{1}\end{matrix}}right],quad {text{ }}{overset {B}{{mathop {left[{begin{matrix}1&2&2\2&1&2\2&2&3\end{matrix}}right]}}}}left[{begin{matrix}a\b\c\end{matrix}}right]=left[{begin{matrix}a_{2}\b_{2}\c_{2}end{matrix}}right],quad {text{ }}{overset {C}{{mathop {left[{begin{matrix}1&-2&2\2&-1&2\2&-2&3end{matrix}}right]}}}}left[{begin{matrix}a\b\cend{matrix}}right]=left[{begin{matrix}a_{3}\b_{3}\c_{3}end{matrix}}right]$

Berggren’s three linear transformations are:

${begin{aligned}&{begin{matrix}-a+2b+2c=a_{1}quad &-2a+b+2c=b_{1}quad &-2a+2b+3c=c_{1}&quad to left[{text{ }}a_{1},{text{ }}b_{1},{text{ }}c_{1}right]\end{matrix}}\&{begin{matrix}+a+2b+2c={{a}_{{2}}}quad &+2a+b+2c={{b}_{{2}}}quad &+2a+2b+3c={{c}_{{2}}}&quad to left[{text{ }}{{a}_{{2}}},{text{ }}{{b}_{{2}}},{text{ }}{{c}_{{2}}}right]\end{matrix}}\&{begin{matrix}+a-2b+2c={{a}_{{3}}}quad &+2a-b+2c={{b}_{{3}}}quad &+2a-2b+3c={{c}_{{3}}}&quad to left[{text{ }}{{a}_{{3}}},{text{ }}{{b}_{{3}}},{text{ }}{{c}_{{3}}}right]\end{matrix}}\&end{aligned}}$

Alternatively, one may also use 3 different matrices found by Price.^[10] These matrices A’, B’, C’ and their corresponding linear transformations are shown below.

${overset {{{A}'}}{{mathop {left[{begin{matrix}2&1&-1\-2&2&2\-2&1&3end{matrix}}right]}}}}left[{begin{matrix}a\b\cend{matrix}}right]=left[{begin{matrix}a_{1}\b_{1}\c_{1}end{matrix}}right],quad {text{ }}{overset {{{B}'}}{{mathop {left[{begin{matrix}2&1&1\2&-2&2\2&-1&3end{matrix}}right]}}}}left[{begin{matrix}a\b\c\end{matrix}}right]=left[{begin{matrix}a_{2}\b_{2}\c_{2}end{matrix}}right],quad {text{ }}{overset {{{C}'}}{{mathop {left[{begin{matrix}2&-1&1\2&2&2\2&1&3\end{matrix}}right]}}}}left[{begin{matrix}a\b\c\end{matrix}}right]=left[{begin{matrix}a_{3}\b_{3}\c_{3}end{matrix}}right]$

Price’s three linear transformations are

${begin{aligned}&{begin{matrix}+2a+b-c=a_{1}quad &-2a+2b+2c=b_{1}quad &-2a+b+3c=c_{1}&quad to left[{text{ }}a_{1},{text{ }}b_{1},{text{ }}c_{1}right]end{matrix}}\&{begin{matrix}+2a+b+c=a_{2}quad &+2a-2b+2c=b_{2}quad &+2a-b+3c=c_{2}&quad to left[{text{ }}a_{2},{text{ }}b_{2},{text{ }}c_{2}right]end{matrix}}\&{begin{matrix}+2a-b+c=a_{3}quad &+2a+2b+2c=b_{3}quad &+2a+b+3c=c_{3}&quad to left[{text{ }}a_{3},{text{ }}b_{3},{text{ }}c_{3}right]end{matrix}}\&end{aligned}}$

The 3 children produced by each of the two sets of matrices are not the same, but each set separately produces all primitive triples.

For example, using [5, 12, 13] as the parent, we get two sets of three children:

$begin{array}{ccc} & left[ 5,12,13 right] & \ A & B & C \ left[ 45,28,53 right] & left[ 55,48,73 right] & left[ 7,24,25 right] end{array} quad quad quad quad quad quad begin{array}{ccc} {} & left[ 5,12,13 right] & {} \ A' & B' & C' \ left[ 9,40,41 right] & left[ 35,12,37right] & left[ 11,60,61 right] end{array}$

Area proportional to sums of squares[edit]

All primitive triples with b+1=c and with a odd can be generated as follows:^[14]

Pythagorean triple	Area	Incircle radius	Circumcircle radius
	$6times (1^{2})$	1	${tfrac {5}{2}}$
	$6times (1^{2}+2^{2})$	2	${tfrac {13}{2}}$
	$6times (1^{2}+2^{2}+3^{2})$	3	${tfrac {25}{2}}$

$left(a,{tfrac {a^{2}-1}{2}},{tfrac {a^{2}+1}{2}}right)$	$6times left[1^{2}+2^{2}+cdots +left({tfrac {a-1}{2}}right)^{2}right]$	${displaystyle {tfrac {a-1}{2}}}$	${displaystyle {tfrac {a^{2}+1}{4}}}$

Height-excess enumeration theorem[edit]

Wade and Wade^[15] first introduced the categorization of Pythagorean triples by their height, defined as c — b, linking 3,4,5 to 5,12,13 and 7,24,25 and so on.

McCullough and Wade^[16] extended this approach, which produces all Pythagorean triples when $k>{frac {h{sqrt {2}}}{d}}:$ Write a positive integer h as pq² with p square-free and q positive. Set d = 2pq if p is odd, or d= pq if p is even. For all pairs (h, k) of positive integers, the triples are given by

$(h+dk,dk+{frac {(dk)^{2}}{2h}},h+dk+{frac {(dk)^{2}}{2h}}).$

The primitive triples occur when gcd(k, h) = 1 and either h=q² with q odd or h=2q².

References[edit]

^ Fibonacci, Leonardo Pisano, (1225), Liber Quadratorum.
^ Fibonacci, Leonardo Pisano . The Book of Squares (Liber Quadratorum). An annotated translation into modern English by L. E. Sigler. (1987) Orlando, FL: Academic Press. ISBN 978-0-12-643130-8
^ Stifel, Michael, (1544), Arithmetica Integra.
^ Ozanam, Jacques (1814). «Recreations in Mathematics and Natural Philosophy». 1. G. Kearsley: 49. Retrieved 2009-11-19.
^ Ozanam, Jacques, (1844). Science and Natural Philosophy: Dr. Hutton’s Translation of Montucla’s edition of Ozanam, revised by Edward Riddle, Thomas Tegg, London. Read online- Cornell University
^ Dickson, L. E. (1920), History of the Theory of Numbers, Vol.II. Diophantine Analysis, Carnegie Institution of Washington, Publication No. 256, 12+803pp Read online — University of Toronto
^ Rukavicka, J. (2013), Dickson’s Method for Generating Pythagorean Triples Revisited, European Journal of Pure and Applied Mathematics ISSN 1307-5543, Vol. 6, No. 3 (2013) p.363-364, online1 online2
^ Horadam, A. F., «Fibonacci number triples», American Mathematical Monthly 68, 1961, 751-753.
^ ^a ^b Bernhart, Frank R.; Price, H. Lee (2005). «Heron’s formula, Descartes circles, and Pythagorean triangles». arXiv:math/0701624v1.
^ ^a ^b Price, H. Lee (2008). «The Pythagorean Tree: A New Species». arXiv:0809.4324 [math.HO].
^ ^a ^b Berggren, B. (1934). «Pytagoreiska trianglar». Tidskrift för elementär matematik, fysik och kemi (in Swedish). 17: 129–139.
^ Carvalho, Alda; Pereira dos Santos, Carlos (2012). «A very useful Pythagorean tree». In Silva, Jorge Nuno (ed.). Proceedings of the recreational mathematics colloquium II, University of Évora, Portugal, April 27–30, 2011. Lisboa: Associação Ludus. pp. 3–15. ISBN 9789899734623.
^ J. L. Poet and D. L. Vestal, Jr. (2005). «Curious Consequences of a Miscopied Quadratic, » College Mathematics Journal 36, 273–277.
^ Barbeau, Edward, Power Play, Mathematical Association of America,1997, p. 51, item 3.
^ Wade, Peter, and Wade, William, «Recursions that produce Pythoagorean triples», College Mathematics Journal 31, March 2000, 98-101.
^ McCullough, Darryl, and Wade, Elizabeth, «Recursive enumeration of Pythagorean triples», College Mathematics Journal 34, March 2003, 107-111.

Источник

План урока:

Теорема Пифагора

Задачи на применение теоремы Пифагора

Пифагоровы тройки

Обратная теорема Пифагора

Формула Герона

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х². Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с²– это площадь большого (на рисунке – синего)квадрата, а х² – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

10:2 = 5

Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а², b²и с² – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а² + b²четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.

Обратная теорема Пифагора

По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А₁В₁С₁ прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.

Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:

1) некоторое условие, которое описывает какое-то геометрическое построение;

2) вывод (или заключение), который делается для условия.

В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.

В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.

Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.

Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона

Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.

Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h²:

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.

Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?

Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.

Источник

Пожалуй, о пифагоровых тройках не слышал только тот, кто не слышал слова «математика», а тот, кто о них слышал, имеет все основания полагать, что о пифагоровых тройках известно всё, что могло быть узнано за их почти четырёхтысячелетнюю историю. Однако, я покажу их с ракурса, который, по-видимому, до сих пор не был известен.

Примем следующее определение: пифагоровой тройкой называется набор трёх натуральных чисел удовлетворяющих уравнению . Если числа не имеют общих делителей, то пифагорова тройка называется примитивной.

Общеизвестна формула Евклида, выражающая пифагорову тройку парой целых чисел , где :

$a=m^2-n^2 \ b=2 m n \ c=m^2+n^2$

Первым шагом в исследовании пространства пифагоровых троек будет переход к другим величинам:

$c-a=2 n^2=2 n cdot n \ a+b-c=2 n cdot (m-n) \ c-b=(m-n)^2=(m-n) cdot (m-n)$

которые обладают следующим свойством:

$НОД (a+b-c, c-a, b)=2 n \ НОД (a+b-c, c-b, a)=(m-n)$

Введём обозначения:

$2 n=t \ m-n=v= tau \ n= varphi$

и установим правило запрета квадратов: любая комбинация величин и/или , стоящая под знаком второй степени, означает произведение двух различных величин. Так:

$c-a=2 n^2=2 n cdot n= varphi t \ a+b-c= 2 n cdot (m-n)=v t \ c-b=(m-n)^2=(m-n) cdot (m-n)=v tau \$

Далее, перепишем исходное условие пифагоровой тройки в виде:

сделаем принятые замены:

и, после сокращения на , окончательно получим условие пифагоровой тройки в новых величинах:

Следующим шагом, сопоставим пифагоровой тройке её матричный образ (далее, опт — образ пифагоровой тройки):

$begin{pmatrix} tau & v \ varphi & t end{pmatrix}$

и примем правило восстановления прообраза:

где:

$a=v tau+v t \ b=v t+varphi t \ c=v tau+v t+ varphi t$

Рассмотрим построение оптов на трёх примерах.

Пример 1

$5^2+12^2=13^2 \ tau=1, v=1, t=4, varphi=2 \ begin{pmatrix} 1 & 1 \ 2 & 4end{pmatrix}$

Пример 2

$8^2+15^2=17^2 \ tau=1, v=2, t=3, varphi=3 \ begin{pmatrix} 1 & 2 \ 3 & 3 end{pmatrix}$

Пример 3

$20^2+21^2=29^2 \ tau=2, v=4, t=3, varphi=3 \ begin{pmatrix} 2 & 4 \ 3 & 3 end{pmatrix}$

Обратим внимание на то, что опт из примера 3 составлен из нижних строк оптов из примеров 1 и 2.

Построение оптов пифагоровых троек из первой сотни показало, что серии троек с характеристиками и играют роль, своего рода, координатных осей — взяв по одной строке из оптов этих серий, составив из них новый опт так, чтобы в его нижней строке значения повторялись и восстановив из него прообраз, мы получим другую пифагорову тройку.

Вот как выглядят на координатной плоскости оптов первые его элементов, красным цветом обозначены опты непримитивных пифагоровых троек:

Пронумеровав серии оптов с характеристиками и мы получим натуральнозначные координаты, а значит, можем определить правило их сложения. Таким образом, пространство пифагоровых троек является координатным.

Примечательным свойством этого пространства является то, что пифагоровы тройки заполняют его без разрывов.

Источник

В математике пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел 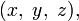удовлетворяющих соотношению Пифагора:

x² + y² = z².

Содержание

1 Свойства
2 Примеры
3 История
4 См. также
5 Ссылки

Свойства

Поскольку уравнение x² + y² = z² однородно, при домножении x, y и z на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть 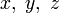x,;y,;z — взаимно простые числа.

Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 (3² + 4² = 5²).

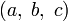
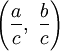
Пифагорова тройка задаёт точку с рациональными координатами $left( frac a c,;frac b c right)$ на единичной окружности x² + y² = 1.

Нетрудно видеть, что в примитивной тройке (x,y,z) числа x и y имеют разную чётность. Любая примитивная пифагорова тройка (x,y,z), где x — нечётно, а y — чётно, однозначно представляется в виде 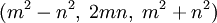для некоторых натуральных взаимно простых чисел m > n разной чётности. Наоборот, любая такая пара (m,;n) задаёт примитивную пифагорову тройку . ^[1]

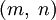
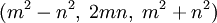
Примеры

Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):

(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (14, 48, 50), (30, 40, 50)…

История

Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

X Всероссийский симпозиум по прикладной и промышленной математике. Санкт — Петербург, 19 мая 2009г.

Доклад: Алгоритм решения Диофантовых уравнений.

В работе рассмотрен метод исследования Диофантовых уравнений и представлены решенные этим методом: — великая теорема Ферма; — поиск Пифагоровых троек и тд. http://referats.protoplex.ru/referats_show/6954.html

См. также

Великая теорема Ферма
Теорема Пифагора

Ссылки

↑ В. Н. Серпинский Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.

Е. А. Горин Степени простых чисел в составе пифагоровых троек // Математическое просвещение. — 2008. — В. 12. — С. 105-125.

Wikimedia Foundation.
2010.

Источник