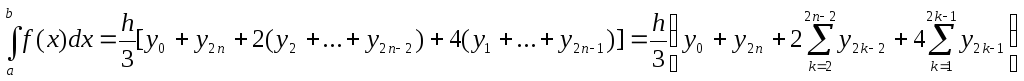Как найти численное значение интеграла - Исправление недочетов и поиск решений вместе с Examum.ru

Численные методы вычисления значения определенного интеграла применяются в том случае, когда первообразная подинтегральной функции не выражается через аналитические функции, и поэтому невозможно вычислить значение по формуле Ньютона-Лейбница. Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.

Численное интегрирование сводится к вычислению площади криволинейной трапеции, ограниченной графиком заданной функции, осью х и вертикальными прямыми ограничивающими отрезок слева и справа. Подинтегральная функция заменяется на более простую, обеспечивающую заданную точность, вычисление интеграла для которой не составляет труда.

Калькулятор ниже вычисляет значение одномерного определенного интеграла численно на заданном отрезке, используя формулы Ньютона-Котеса, частными случаями которых являются:

Метод прямоугольников
Метод трапеций
Метод парабол (Симпсона)

Интеграл численным методом по формулам Ньютона-Котеса

Число частичных интервалов

Точность вычисления

Знаков после запятой: 6

Значение определенного интеграла

Геометрический вид интеграла

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Численное интегрирование с использованием функций Ньютона Котеса

При использовании функций Ньютона-Котеса отрезок интегрирования разбивается на несколько равных отрезков точками x₁,x₂,x₃..x_n.
Подинтегральную функцию заменяют интерполяционным многочленом Лагранжа различной степени, интегрируя который, получают формулу численного интегрирования различного порядка точности.

В итоге, приближенное значение определенного интеграла вычисляется, как сумма значений подинтегральной функции в узлах, помноженных на некоторые константы W_i (веса):
$Iapprox sum _{{i=1}}^{{n}}{W_i}f(x_{i})+R_n$

R_n — остаток или погрешность.
n — общее количество точек.
Сумма в формуле — квадратурное правило (метод).

В справочнике Квадратурные функции Ньютона-Котеса, мы собрали наиболее часто встречающиеся квадратурные правила, для интегрирования по равным отрезкам. Зарегистрированные пользователи могут добавлять в этот справочник новые правила.

Границы отрезка интегрирования

В зависимости от того, входят ли граничные точки отрезка в расчет, выделяют замкнутые и открытые квадратурные правила.

Открытые правила, (правила, в которых граничные точки не включаются в расчет) удобно использовать в том случае, если подинтегральная функция не определена в некоторых точках.
Например, используя метод прямоугольников мы сможем вычислим приблизительное значение интеграла функции ln(x) на отрезке (0,1), несмотря на то, что ln(0) не существует.

Замкнутые правила, напротив, используют значения функции в граничных точках для вычислений интеграла, ровно так же как и в остальных узлах.

Можно придумать правила, которые открыты только с одной стороны. Простейшим случаем таких правил являются правила левых и правых прямоугольников.

Погрешность вычисления

В целом с увеличением количества узлов в правиле (при повышении степени интерполирующего полинома) возрастает точность вычисления интеграла. Однако для некоторых функций это может и не быть справедливо.
Впервые анализ этой особенности опубликовал Карл Рунге, немецкий математик, занимавшийся исследованием численных методов.
Он заметил, интерполирующий полином с равномерным разбиением отрезка для функции $frac{1}{1+25x^2}$ перестает сходиться в диапазоне значений 0.726.. ≤ |x| <1 при увеличении степени полинома.
В выражении для вычисления погрешности участвует интервал h, факториал от количества разбиений, которые при увеличении степени полинома уменьшают значение погрешности, но для некоторых функций значения производной, также участвующие в выражении погрешности, растут быстрее с увеличением ее порядка.

Кроме этого, при увеличении степени интерполирующего полинома Лагранжа, возникают веса, имеющие отрицательные значения. Данный факт негативно сказывается на вычислительной погрешности. Калькулятор выдает графическое представление промежуточных результатов вычисления квадратурной функции. Для положительных коэффициентов W_i это выглядит ровно так же, как принято отображать сумму Римана. При наличии отрицательных значений коэффициентов W_i на графике появляются значения интегральной суммы с противоположным знаком, суммарная ширина положительных и отрицательных интегральных сумм становится больше, чем длина интегрируемого отрезка. Этот эффект можно наблюдать в следующем примере: Замкнутое правила Ньютона-Котеса с 11-ю узлами

Принимая во внимание эти особенности, правила с полиномами степеней >10 применять не рекомендуется.

Для увеличения точности численного интегрирования, можно разбить отрезок на несколько частей — частичных интервалов, и для каждой части отдельно вычислить приближенное значение интеграла. Сумма значений интеграла по всем частичным интервалам даст нам значение интеграла на всем отрезке. Кроме того можно комбинировать различные правила друг с другом в любой последовательности.

Для исследования работы с заданной функцией новых, основанных на формулах Ньютона-Котеса правил, можно воспользоваться базовым калькулятором, в котором веса задаются в явном виде:

Численное интегрирование с заданными весами Ньютона-Котеса

Веса формулы Ньютона-Котеса

Перечислите веса через запятую, в самом начале укажите общий множитель. Можно указывать коэффициенты в виде простой дроби, например, так: 3/4. Пример весов для метода Симпсона: 1/3,1,4,1.

Число частичных интервалов

Точность вычисления

Знаков после запятой: 6

Значение определенного интеграла

Геометрический вид интеграла

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Веса задаются через запятую, допускаются как целые, так и действительные числа с точкой, для отделения дробной части. Можно задать вес в виде простой дроби, например, вот так: 1/90.
Первый коэффициент в списке весов — это общий множитель, его тоже можно задать в виде простой дроби или задать = 1, если общего множителя нет.

Например, веса: 3/8,1,3,3,1 определяют Метод Симпсона 3/8

Правила Ньютона-Котеса несовершенны, для реальных приложений следует использовать более эффективные методы, например метод Гаусса-Кронрода, о котором мы напишем в следующих статьях.

Литература:

Н.С.Бахвалов Численные методы, 2012
У.Г.Пирумов Численные методы, 2006
Д.Каханер, К.Моулер, С.Нэш Численные методы и программное обеспечение, 1989
Р.В. Хемминг Численные методы для научных работников и инженеров, 1972
M. Abramovitz и I. Stegun Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables, 1973

Источник

Печатать книгу

Численное интегрирование

Сайт:	Электронные курсы ТПУ
Курс:	Информационные технологии 1
Книга:	Численное интегрирование
Напечатано::	Гость
Дата:	Вторник, 30 Май 2023, 07:16

Численное интегрирование
1. Методы прямоугольников
2. Метод трапеций
3. Процедура вычисления интеграла
4. Вычисление интегралов с заданной точностью и оценка методов интегрирования
5. Основная часть программы

Численное интегрирование

Задача вычисления интегралов возникает во многих областях прикладной математики. В большинстве случаев не удается найти аналитической формулы, т. е. выразить неопределенный интеграл в виде алгебраических и трансцендентных функций. Даже если аналитическая формула находится, то она получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем другими способами. Распространенными являются также случаи, когда подынтегральная функция задается графиком или таблицей экспериментально полученных значений. В таких ситуациях используют различные методы численного интегрирования, которые основаны на том, что интеграл представляется в виде предела интегральной суммы (суммы площадей), и позволяют определить эту сумму с приемлемой точностью.

Пусть требуется вычислить определенный интеграл

при условии, что A и B конечны и f(x) является непрерывной функцией x во всем интервале A ≤ x ≤ B. Значение интеграла I представляет собой площадь, ограниченную кривой f(x), осью x и прямыми x = A, x = B. Вычисление I проводится путем разбиения интервала от A до B на множество меньших интервалов, приближенным нахождением площади каждой полоски, получающейся при таком разбиении, и дальнейшем суммировании площадей этих полосок.

Суть методов численного интегрирования состоит в замене подынтегральной функции f(x) вспомогательной, интеграл от которой легко вычисляется в элементарных функциях. Обычно f(x) заменяется некоторым интерполяционным многочленом, что приводит к квадратурным формулам:

где x_i – узлы интерполяции;

i – произвольный номер узла;

C_i – коэффициенты;

R – остаточный член, или погрешность метода.

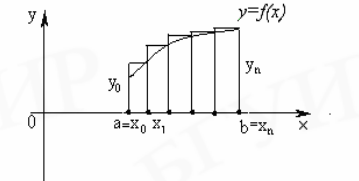
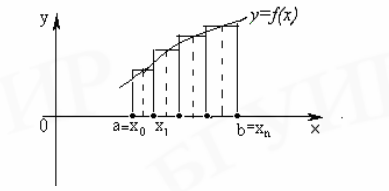
Неучет (отбрасывание) R приводит к погрешности усечения. К этим погрешностям в процессе вычислений добавляются погрешности округления. Геометрическая интерпретация численного интегрирования представлена на рис. 5.1. и 5.2.

1. Методы прямоугольников

Самыми простыми методами численного интегрирования являются методы прямоугольников. При этом непосредственно используется замена определенного интеграла интегральной суммой:

, h_i = x_i – x_i_—₁ , x_i_—₁ ≤ z_i ≤ x_i

В качестве точек z_i могут выбираться левые (z _i= x_i_—₁) или правые (z_i= x_i) границы элементарных отрезков. Обозначая y_i = f(x_i) , получим формулы:

метод левых прямоугольников: I = h₁y₀ + h₂y₁ +…+ h_ny_{n —}₁+ R;
метод правых прямоугольников: I = h₁y₁ + h₂y₂ +…+ h_ny_n+ R;
более точным является метод средних прямоугольников, использующий значения функции в средних точках элементарных отрезков:

;

x_i_-1/2= 0,5(x_i_-1+ x_i) = x_i_-1 + 0,5 h_i, i = 1, 2, …, n.

Для частного случая h_i = h = const формулы примут вид

;

, h = (B – A) / n.

Если координату выразить через начальную точку и принять, что I ≈ S, то получим формулы, готовые для применения в операторе цикла с переменной:

– для метода левых прямоугольников;

– для метода правых прямоугольников;

– для метода средних прямоугольников.

Рис. 5.1. Графическая интерпретация методов прямоугольников

2. Метод трапеций

В данном методе f(x) заменяется на линейный интерполяционный многочлен, т. е. на элементарном отрезке [x_{i —}₁, x_i] подынтегральная функция представляет собой отрезок прямой линии. Значение I в пределах [x_{i —}₁, x_i], равное площади криволинейной фигуры, заменяется площадью прямоугольной трапеции с высотой h_i и основаниями f(x_{i —}₁), f(x_i):

S_i = 0,5 (y_i_-1 + y_i) h_i, i = 1, 2, …, n.

После сложения этих соотношений получим формулу трапеций

Если шаг интегрирования постоянный (h_i = h = const), то

Если координату выразить через начальную точку и принять, что I » S, то получим формулу, готовую для применения в операторе цикла с переменной

Рис. 5.2. Графическая интерпретация метода трапеций

3. Процедура вычисления интеграла

Процедура вычисления интеграла при заданном числе разбиений и границами интегрирования должна иметь входные параметры этих величин и выходной параметр результата. Выходной параметр должен содержать перед собой ключевое слово var для передачи параметра по ссылке.

Здесь должен вычисляться шаг в соответствии с числом разбиений.

Сумма может вычисляться при помощи цикла for по числу разбиений или при помощи циклов repeat или while с перемещением текущей точки от начальной до конечной. Например, для метода правых прямоугольников процедура может быть описана так:

procedure integral(a,b:real;n:integer; var s:real);

var i:integer; h:real;

begin

h:=abs(b-a)/n; s:=0;

for i:=1 to n do

s:=s+h*f(a+h*i);

end;

Конечно, перед описанием процедуры необходимо описать подынтегральную функцию f(x). Смотрите описание функций в 3.1.

Замечание! При вычислении интеграла функция должна браться по модулю, т. к. площадь фигуры всегда положительна, независимо от того, что функция может быть и отрицательной. Для упрощения программы модуль можно вставить сразу в описание функции.

4. Вычисление интегралов с заданной точностью и оценка методов интегрирования

Оценка погрешности усечения R в формулах численного интегрирования оказывается трудоемкой и малоэффективной из-за трудностей оценки производных высокого порядка подынтегральных функций. Поэтому в практических расчетах для достижения требуемой точности вычислений или допустимой погрешности E используют правило Рунге.

Согласно этому правилу вычисление заданного интеграла проводят для разных интервалов разбиения отрезка [A,B]. Так, если начальное число интервалов разбиения есть n и соответствующее ему приближенное значение интеграла – I_n, то для числа интервалов 2n получим значение интеграла I_2n. Число интервалов можно увеличивать в 2, 3 и т. д. раз по сравнению с базовым значением n. При двукратном увеличении числа отрезков погрешность D приближенного значения интеграла для методов прямоугольников и трапеций оценивается как

Δ = | I_n – I_2n | / 3.

Если Δ > E, то количество интервалов разбиения [A,B] опять увеличивают вдвое, т. е. значение I вычисляют для 4n. Такое удвоение повторяют до тех пор, пока не выполнится условие Δ < E. Необходимо помнить, что общая погрешность вычислений, равная сумме погрешностей усечения и округления, сначала с ростом интервалов разбиения уменьшается за счет уменьшения ошибки усечения до некоторого «критического» значения n_кр, а затем увеличивается из-за увеличения ошибок округления.

Таким образом, не для всякой функции можно получить результат с заданной погрешностью.

Методы левых и правых прямоугольников практически не применяются из-за их низкой точности.
В некоторых случаях метод средних дает лучшую точность, чем метод трапеций.

5. Основная часть программы

Основная часть программы должна содержать ввод с клавиатуры начального числа разбиений и погрешности вычислений. Для обеспечения заданной точности интеграла процедура его вычисления должна выполняться в цикле. Причём сначала сохраняется старое значение интеграла, затем увеличивается число разбиений и вычисляется новое значение интеграла. Цикл работает пока разница между старым и новым значениями интеграла не станет меньше заданной точности.

При выводе результата полезно также вывести конечное число разбиений, чтобы знать, на сколько частей нужно разбить отрезок для обеспечения заданной точности вычисления интеграла.

Источник

Численное интегрирование

Задача численного
интегрирования состоит в том, чтобы
найти численное значение определенного
интеграла

,
(1)

где

— функция, непрерывная на отрезке
интегрирования
.
Формулы для решения этой задачи называются
квадратурными. Квадратурная формула
позволяет вместо точного значения
интеграла (1) найти некоторое его
приближенное значение
.
Разность точного и приближенного
значений интеграла называется абсолютной
погрешностью квадратурной формулы (или
численного метода),

Квадратурные
формулы используют для вычисления
интеграла (1) значения
,
,
…,

функции

в точках

отрезка
.
Квадратурная формула имеет вид

,
(2)

где

— некоторые коэффициенты, которые
называют весовыми.

Напомним
геометрический смысл определенного
интеграла:

выражает площадь соответствующей
криволинейной трапеции (фигуры,
ограниченной графиком функции
,
прямыми
и
осью
).

Рассмотрим два
подхода к решению задачи численного
интегрирования.

Разобьем отрезок
интегрирования

на

частичных отрезков, вычислим интегралы
на частичных отрезках. Интеграл на всем
отрезке интегрирования

равен сумме интегралов на частичных
отрезках (свойство аддитивности
определенного интеграла).
Вычислим
,
заменяя подынтегральную функцию
на всем отрезке интегрирования

интерполяционным полиномом Лагранжа
,
построенным на
узлах
.

Обозначим через
максимальное
по модулю значение производной
—
го порядка функции
на
отрезке:

Рассмотрим варианты
решения данной задачи.

Формулы прямоугольников

Для простоты
разобьем отрезок интегрирования

на

частей точками, равноудаленными друг
от друга:

так, что будет выполняться равенство:
,
где
.

Аппроксимируем
площадь под графиком функции
суммой
площадей прямоугольников с основанием

и высотой
,
где
.

Причем, если взять
(левую
крайнюю точку частичного отрезка), то
получим формулу левых
прямоугольников:

Мы видим, что
весовые коэффициенты формулы левых
прямоугольников в случае равностоящих
узлов равны
,
кроме коэффициента при
,
который равен 0.

Абсолютная
погрешность формулы левых прямоугольников
определяется выражением:

где
.

Мы
видим, что погрешность метода левых
прямоугольников имеет тот же порядок,
что шаг интегрирования
(первый
порядок по
).
Поскольку для функций вида

,
то для таких функций формула левых
прямоугольников является точной.

А если взять(правую
крайнюю точку частичного отрезка), то
получим формулу правых
прямоугольников:

Погрешность метода
правых прямоугольников имеет тот же
порядок, что и шаг интегрирования
.

В случае, когда мы
берем среднюю точку
,
получаем формулу средних прямоугольников:

Абсолютная
погрешность формулы средних прямоугольников
оценивается выражением:

Погрешность формулы
средних прямоугольников имеет второй
порядок по
().

Наиболее
употребительной является формула
средних прямоугольников.

Формула трапеций

Заменим площадь
криволинейной трапеции суммой площадей
прямолинейных трапеций, построенных
на частичных отрезках
,
.
Площадь элементарной прямолинейной
трапеции равна:

а интеграл равен:

Оценка абсолютной
погрешности на всем отрезке интегрирования
определяется выражением:

Погрешность метода
трапеций имеет тот же порядок, что и
.
Для функций вида
(полиномов
первой степени) формула трапеций является
точной.

Формула Симпсона
(формула парабол).

Теперь аппроксимируем
функцию на элементарном отрезке
параболой. По сравнению с предыдущими
способами вдвое уменьшим расстояние
между узлами
.
Таким образом, получаем
частичных
отрезков и
узлов
интегрирования. Значения функции в
узлах:.
Квадратурная формула Симпсона имеет
вид:

Абсолютная
погрешность формулы Симпсона оценивается
выражением:

Абсолютная
погрешность формулы Симпсона имеет тот
же порядок, что и

(четвертый порядок точности). Формула
Симпсона точна для полиномов степени
.

При приближенном
вычислении определенного интеграла на
компьютере оценка точности вычислений
по приведенным выше формулам для
погрешностей, как правило, не применяется
ввиду трудности нахождения.
В таких случаях используют правило
Рунге.

Правило Рунге
основано на соотношении:

,
(3)

где
,

— приближенные значения определенного
интеграла, вычисленные при разбиении
отрезка интегрирования на n
и 2n
частей соответственно;
—
порядок метода;
— заданная точность. При каждом последующем
приближении число отрезков разбиения
удваивается. Если условие

выполнено, за приближенное значение
интеграла принимается значение
,
т.е..Так
как оценка осуществляется после
вычисления, то она является апостериорной.

Напомним порядки
методов (по
):

№	Название метода	Порядок метода
1	левых прямоугольников	1
2	правых прямоугольников	1
3	средних прямоугольников	2
4	трапеций	2
5	парабол (Симпсона)	4

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Интеграл численным методом по формулам Ньютона-Котеса

Численное интегрирование с использованием функций Ньютона Котеса

Границы отрезка интегрирования

Погрешность вычисления

Численное интегрирование с заданными весами Ньютона-Котеса

Численное интегрирование

Оглавление

Численное интегрирование

1. Методы прямоугольников

2. Метод трапеций

3. Процедура вычисления интеграла

4. Вычисление интегралов с заданной точностью и оценка методов интегрирования

5. Основная часть программы

Численное интегрирование

Формулы прямоугольников