На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.

Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
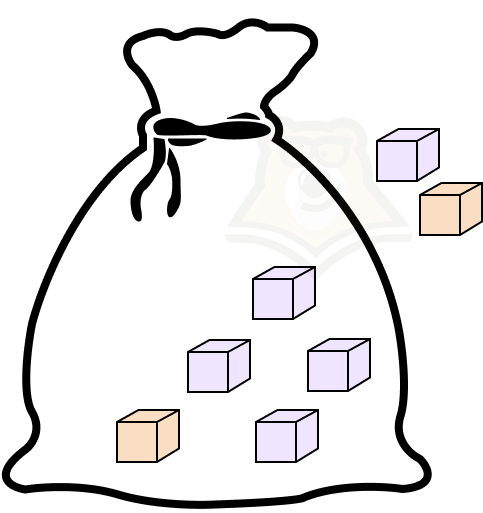
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Вероятность есть числовая характеристика возможности появления случайного события. При этом предполагается, что условия эксперимента могут быть воспроизведены неограниченное число раз. Это нематематическое определение носит скорее интуитивный характер. Придадим ему более точный смысл.
Рассмотрим некоторый случайный эксперимент. Пусть в результате данного эксперимента может произойти несколько исходов (случайных событий). К примеру, при бросании кубика может произойти шесть различных исходов (может выпасть число от 1 до 6).
Назовем исход благоприятным для случайного события А, если событие А следует из такого исхода. Пусть, например, событие А состоит в том, что выпавшее на грани кубика число четно. Благоприятными для этого события будут три исхода эксперимента: выпадение 2, 4 и 6 очков.
Будем называть равновозможными исходы, имеющие одинаковые шансы. Равновозможность определяется нестрого, однако считается интуитивно ясным и лишь поясняется примерами. Для каждого из таких событий характерно то, что ни одно из них не является объективно более возможным, чем другие. В практических задачах исследователь сам решает, какие события считать равновозможными (как правило, исходя из некой симметрии в условиях задачи).
Определение:Пусть данный эксперимент имеет N равновозможных и несовместных исходов. Вероятностью P(A) события А называется отношение числа благоприятных исходов m(A) к общему числу N несовместных равновозможных исходов:

Данное равенство называется классическим определением вероятности.
Вероятность можно вычислять в процентах. Например, выражения P(A) = 90% и P(A) = 0,9 эквивалентны.
Для любого случайного события А
Во-первых, по определению вероятность неотрицательна. Во-вторых, число благоприятных исходов m(A) не больше общего числа исходов N. Поэтому,
Пример 1:В урне находятся 4 белых и 6 черных шаров. Какова вероятность, что вынутый наугад шар будет белым?
Всего эксперимент имеет десять исходов (можно вынуть любой из 10 шаров). Благоприятными будут 4 исхода. Значит, вероятность этого события равна 
Пример 2. Пусть опыт состоит в последовательном бросании двух кубиков. Найдем вероятность события B – «в сумме выпало 8 очков» и вероятность события C – «в сумме выпало 12 очков».
Очевидно, что при бросании двух кубиков всего может быть получено 36 равновозможных несовместных исходов: n = 36 (каждому из 6 различных случаев выпадения очков на первом кубике отвечает 6 случаев выпадения различного числа очков на втором кубике). Событию С благоприятен лишь один исход: случай выпадения двух «шестерок», поэтому m(C) = 1, и 

Чтобы пользоваться классическим определением вероятности, нужно уметь подсчитывать общее число исходов эксперимента и число благоприятных исходов. Такой подсчет сводится к перебору вариантов, т.е. к задачам комбинаторики. Рассмотрим, как комбинаторные формулы применяются в задачах теории вероятностей.
Многие случайные события моделируются экспериментами с урной и шарами. Шары из урны можно доставать по-разному: шар можно каждый раз возвращать в урну, а можно этого не делать; выбранные шары можно упорядочивать или не упорядочивать и т.д. Таким образом, существуют различные схемы выбора. В каждой из этих схем общее число исходов и число благоприятных исходов подсчитывается по-разному. Рассмотрим основные схемы выбора и соответствующие задачи.
Задача 1. (Схема выбора без возвращения и упорядочения).В урне 3 белых и 7 черных шаров. Какова вероятность того, что из четырех наугад выбранных шаров ровно один будет белый? Какова вероятность, что белых шаров будет ровно два?
Решение:вынуть 4 шара – это все равно, что вынуть по одному шару, не возвращая их обратно в урну. Поэтому такая ситуация описывается схемой без возвращения и без упорядочения. Общее число исходов этого случайного эксперимента равно числу способов выбрать 4 шара из 10, т.е. числу сочетаний 
В первом случай при благоприятном исходе среди четырех шаров один белый, а остальные три – черные (событие А). Белый шар можно выбрать тремя способами (их всего три), три черных можно выбрать 

Значит, искомая вероятность
Найдем число благоприятных исходов во втором случае (два белых, два черных шара – событие B). Пару белых шаров можно выбрать 
Каждая пара белых шаров может сочетаться с каждой парой черных. Поэтому всего благоприятных исходов m(A) = 3·21 = 63. Значит вероятность второго события (B):
Задача 2. (Схема выбора без возвращения c упорядочением).В урне находятся карточки с цифрами от 0 до 5. Наугад достают две карточки и складывают подряд. Какова вероятность того, что полученное двузначное число кратно семи?
Решение:В отличие от предыдущей задачи, теперь важен порядок, в котором вынимают карточки, но по-прежнему карточки в урну не возвращают. Значит, в этом случае общее число исходов равно числу размещений из 6 по 2, т.е. 
Задача 3. (Схема выбора с возвращением и без упорядочения).В кондитерской продается семь видов пирожных. Очередной покупатель выбил чек на четыре пирожных. Найти вероятность того, что заказаны:
а) пирожные одного вида;
б) пирожные разных видов;
в) по два пирожных разных видов.
Решение:Результатом опыта являются всевозможные наборы из четырех пирожных, отличающиеся составом. Наборы из одних и тех же пирожных, но расположенных в различном порядке, считаются одинаковыми (схема без упорядочения). При этом отдельные наборы могут содержать повторяющиеся элементы (схема с возвращением). Поэтому общее число исходов равно числу сочетаний с повторениями:
В первом случае благоприятных исходов 7 (наборы из пирожных каждого из семи видов). Значит, вероятность
Во втором случае благоприятными являются всевозможные наборы из четырех различных пирожных, выбранных из семи (порядок не важен). Ясно, что это число сочетаний из 7 по 4:
Поэтому вероятность второго события
Рассмотрим третий случай. Благоприятный исход представляет собой две пары одинаковых пирожных. Таких наборов ровно столько, сколько различных пар можно составить из 7 предметов, т.е. 
Задача 4. (Схема выбора с возвращением и с упорядочением).Телефонная книга раскрывается наудачу и выбирается случайный номер телефона. Считая, что телефонные номера состоят из семи цифр, причем все комбинации равновероятны, найти вероятность того, что все цифры в номере различны.
Решение:Заметим, что условие задачи разрешает любые номера (такие, например, как 0012413, 0123456 и даже 0000000). Поскольку всего цифр 10, а номера семизначные, общее число номеров равно N = 10 7 = 10000000 (число размещений с повторениями из 10 элементов по 7). Благоприятные исходы составляют все различные наборы из семи цифр, отличающиеся также порядком (число размещений без повторений из 10 элементов по 7). Значит, благоприятных исходов
Итак,
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10572 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Если вас интересует вопрос заголовка, вы наверняка студент или школьник, столкнувшийся с новым для себя предметом. Задачи теории вероятностей сейчас решают и школьники пятых классов продвинутых школ, и старшеклассники перед ЕГЭ, и студенты буквально всех специальностей — от географов до математиков. Что же это за предмет такой, и как к нему подойти?
Вероятность. Что это?
Теория вероятностей, как следует из названия, имеет дело с вероятностями. Нас окружают множество вещей и явлений, о которых, как бы ни была развита наука, нельзя сделать точных прогнозов.
Мы не знаем, какую карту вытянем из колоды наугад или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, можем строить прогнозы и вычислять вероятности этих случайных событий.
Таким образом, мы сталкиваемся с основным понятием случайного события — явления, поведение которого невозможно предсказать, опыта, результат которого заранее невозможно вычислить и т.п. Именно вероятности событий вычисляются в типовых задачах.
Вероятность — это некоторая, строго говоря, функция, принимающая значения от 0 до 1 и характеризующая данное случайное событие. 0 — событие практически невозможно, 1 — событие практически достоверно, 0,5 (или «50 на 50») — с равной вероятностью событие произойдет или нет.
Алгоритм решения задач на вероятность
Подробнее с основами теории вероятностей можно ознакомиться, например, в онлайн учебнике.
А теперь не будем ходить вокруг да около, и сформулируем схему, по которой следует решать стандартные учебные задачи на вычисление вероятности случайного события, а затем ниже на примерах проиллюстрируем ее применение.
- Внимательно прочитать задачу и понять, что именно происходит (что из какого ящика вытаскивается, что где лежало, сколько приборов работает и т.п.)
- Найти основной вопрос задачи вроде «вычислить вероятность того, что . » и вот это многоточие записать в виде события, вероятность которого надо найти.
- Событие записано. Теперь надо понять, к какой «схеме» теории вероятностей относится задача, чтобы правильно выбрать формулы для решения. Ответьте на тестовые вопросы типа:
- происходит одно испытание (например, выбрасывание двух костей) или несколько (например, проверка 10 приборов);
- если испытаний несколько, зависимы ли результаты одного от других (зависимость или независимость событий);
- событие происходит в единственной ситуации или задача говорит о нескольких возможных гипотезах (например, шар вынимается из любого ящика из трех, или из конкретного).
Чем больше опыт решения задач, тем легче будет определить, какие формулы подходят.
Как решать задачи: классическая вероятность
Пример 1. В группе из 30 студентов на контрольной работе 6 студентов получили «5», 10 студентов – «4», 9 студентов – «3», остальные – «2». Найти вероятность того, что 3 студента, вызванные к доске, получили по контрольной работе «2».
Начинаем решение по пунктам, описанным выше.
- В задаче речь идет о выборе 3 студентов из группы, которые удовлетворяют определенным условиям.
- Вводим основное событие $X$ = (Все 3 студента, вызванные к доске, получили по контрольной работе «2»).
- Так как в задаче происходит только одно испытание и оно связано с отбором/выбором по определенному условию, речь идет о классическом определении вероятности. Запишем формулу: $P=m/n$, где $m$ – число исходов, благоприятствующих осуществлению события $X$, а $n$ – число всех равновозможных элементарных исходов.
- Теперь необходимо найти значения $m$ и $n$ для этой задачи. Сначала найдем число всех возможных исходов — число способов выбрать 3 студентов из 30. Так как порядок выбора не имеет значения, это число сочетаний из 30 по 3: $$n=C_<30>^3=frac<30!><3!27!>=frac<28cdot 29 cdot 30><1cdot 2 cdot 3>=4060.$$ Найдем число способов вызвать только студентов, получивших «2». Всего таких студентов было $30-6-10-9=5$ человек, поэтому $$m=C_<5>^3=frac<5!><3!2!>=frac<4 cdot 5><1cdot 2>=10.$$
- Получаем вероятность: $$P(X)=frac=frac<10><4060>=0,002.$$ Задача решена.
Некогда решать? Найди решенную задачу
Готовые решения задач по любым разделам теории вероятностей, более 10000 примеров! Найди свою задачу:
Как решать задачи: формула Бернулли
Пример 2. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз?
Снова по схеме решения задач на вероятность рассматриваем данную задачу:
- В задаче идет речь о серии одинаковых испытаний — бросаний монеты.
- Вводим основное событие $X$ = (При 8 бросаниях монеты герб выпадет 5 раз).
- Так как в задаче происходит несколько испытаний, и вероятность появления события (герба) одинакова в каждом испытании, речь идет о схеме Бернулли. Запишем формулу Бернулли, которая описывает вероятность того, что из $n$ бросков монет герб выпадет ровно $k$ раз: $$ P_(k)=C_n^k cdot p^k cdot (1-p)^.$$
- Записываем данные из условия задачи: $n=8, p=0,5$ (вероятность выпадения герба в каждом броске равна 0,5) и $k=5$
- Подставляем и получаем вероятность: $$ P(X)=P_<8>(5)=C_8^5 cdot 0,5^5 cdot (1-0,5)^<8-5>=frac<8!><5!3!>cdot 0,5^8=frac<6cdot 7 cdot 8><1cdot 2 cdot 3>cdot 0,5^8= 0,219.$$ Задача решена.
И это все? Конечно, нет.
Выше мы упомянули только малую часть тем и формул теории вероятностей, для более подробного изучения вы можете посмотреть учебник онлайн на данном сайте (или скачать классические учебники по ТВ), ознакомиться со статьями по решению вероятностных задач, бесплатными примерами, воспользоваться онлайн калькуляторами. Удачи!
Теория вероятностей (тервер) – раздел математики, который изучает случайные события и их свойства. Ознакомиться с ней нужно, чтобы понимать, как принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно «предсказать» исход события.
Я не станут грузить вас сложными формулами – желающие углубленно заняться тервером могут сделать это по книге В. Е. Гмурмана «Теория вероятностей и математическая статистика». В статье покажу простые примеры для понимания зависимых и независимых событий, расскажу о состоянии неопределенности и интуитивном знании.
Материал полезен широкому кругу читателей.

Вероятность в зависимых событиях
Вы решаете отправить в подарок другу балык. Знаете номер дома, подъезд, этаж. Курьер просит называть номер квартиры. С мучительными усилиями вспоминаете, что в доме по три двери на площадку, но дальше – туман. Давайте рассчитаем, сможет ли курьер попасть в нужную квартиру с первого раза.
Имеем три варианта развития событий:
- Курьер звонит в первую (1) дверь.
- Курьер звонит во вторую (2) дверь.
- Курьер звонит в третью (3) дверь.
Но в истории участвует еще один человек: ваш друг. И событийность в его случае выглядит так:
- Друг за первой (1) дверью.
- Друг за второй (2) дверью.
- Друг за третьей (3) дверью.
Прежде чем пойти дальше, введем определение вероятности – количество благоприятных исходов к вероятному числу событий.
Теперь соберем данные в таблицу (таблица 1). Всего — 9 исходов. Отметим положительные (курьеру откроет друг) – их 3. Получается, что вероятность с первого раза позвонить в дверь к нужному человеку – 3/9 или 1/3. Если вам нравится видеть вероятность в процентах, умножьте результат на 100%.
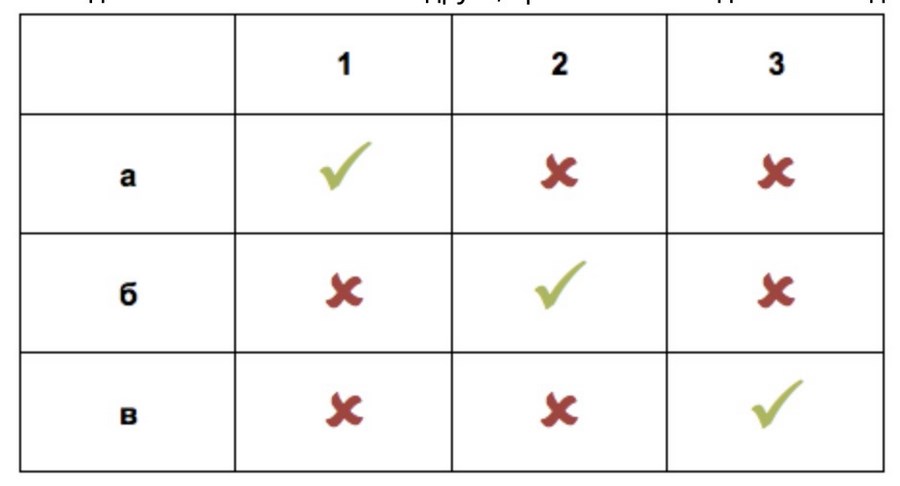
Представим, что курьер ошибся, и за дверью оказалась сногсшибательная блондинка в коротком халате. Для курьера исход положительный, для вас – нет. Поэтому считаем новую вероятность:
- Курьер звонит в первую (1) квартиру.
- Курьер звонит во вторую (2) квартиру.
То же самое с другом:
- Друг ждет в первой (1) квартире.
- Друг ждет во второй (2) квартире.
Теперь у нас 4 варианта и 2 – выигрышные (таблица 2). Вероятность со второго раза попасть в квартиру друга – 1/2. Она уменьшилась из-за зависимости событий: мы уже исключили неблагоприятный исход и расчёт нужно производить заново. Если курьер настолько невезуч, что промахнется во второй раз, вероятность попасть по адресу в третий раз – 100%. Опытным путем мы проверили, что за двумя предыдущими дверьми балык никто не ждет.
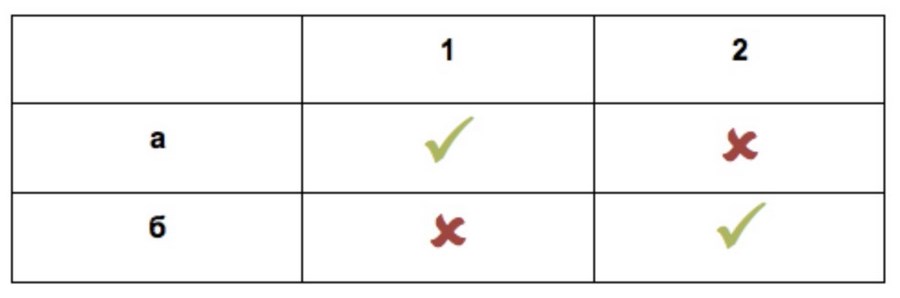
Пример с курьером — начальный уровень тервера. Он применим для бытовых нужд: предугадать вероятность побочного эффекта от антибиотиков, выбрать из разнообразия бабушкиных пирожков пирожок с повидлом и др.
На экзамене по теории вероятности советский математик и автор учебника Елена Вентцель спросила:
— Кому все понятно? Поднимите руки.
В аудитории живо взметнулся лес рук.
— Отлично! Остальные свободны, оценка – пять баллов! Поднявшие руки – останьтесь. За годы преподавания я так и не поняла большей части тервера. Рада, что вы мне все сейчас объясните.
Байка с математического факультета
Вероятность в независимых событиях
Независимые события не влияют друг на друга: количество благоприятных исходов в каждом новом событии не меняется.
Регина Тодоренко и Леся Никитюк в рамках программы «Орел и Решка» приехали в США. Обе хотят провести уик-энд «по богатому» и кидают монетку. Леся поставила на орла, Регина – на решку. Вероятность уехать на собственном авто у девушек одинакова: 1/2. На это раз повезло Лесе. Впрочем, как в следующей поездке тоже.

Теперь определим, могут ли независимые события происходить подряд с одним и тем же исходом. Лесе везло уже два раза и выпадал «орел». Повезет ли в третий раз? Составим список возможных исходов:
- Орел, орел, орел.
- Орел, орел, решка.
- Орел, решка, орел.
- Орел, решка, решка.
- Решка, орел, орел.
- Решка, орел, решка.
- Решка, решка, орел.
- Решка, решка, решка.
По результату видно: вероятность определенной последовательности каждый раз меньше на вероятность одного события. То есть вероятность определенной последовательности – произведение вероятностей каждого события. Если в одном событии вероятность 1/2, то в трех: 1/2*1/2*1/2=1/8.
Как человек принимает решения в состоянии неопределённости
Часть мозга, которая ответственна за оценку ситуации связана с медиаторной системой — центром мотивационных и эмоциональных процессов. Логика и эмоции часто конфликтуют между собой, поэтому решение принимается случайным образом.
У моей подруги аллергия на виноград. Но в студенчестве она не могла отказаться от бокала вина на вечеринке. Часто ее дерзость оставалась безнаказанной и организм нормально воспринимал аллерген. Реже протестовал: у подруги появлялись отеки на лице и в горле. В эти моменты ее левое полушарие отчаянно искало закономерность и просчитывало вероятность наступления аллергической реакции, правое же шептало: «Не пей, лицо распухнет!». Она могла вывести количество благоприятных исходов математическим путем и пить вино без опасений, но эмоции оказались сильней. Подруга раз и навсегда отказалась от любых продуктов с виноградом.
Хороший пример принятия решений описан в книге Млодинова «(Не) совершенная случайность». Допустим, вы отправили рассказ в четыре издательства. От каждого получили отказ. На эмоциях вы придете к мысли: рассказ ужасный! Хотя, если изучить биографии популярных писателей, может оказаться, что дело не в вас. Отказы в публикации получали Стивен Кинг, Джоан Роулинг, Виктор Франкл. Такие истории случались вовсе не из-за отсутствия у них дара: просто в одном издательстве редактор не понял тонкую философию автора, в другом – спешил домой и проставил визу не читая.
Почему интуитивное знание всегда противоречит статистике
Моя бабушка считает: в Албании убивают на каждом шагу. Хотя в стране она не была и новостей о не слышала: ей так кажется интуитивно. Наверняка и вы не раз испытывали подобное чувство. Оно называется интуитивное знание – внутреннее убеждение, что собственная оценка более правдива, чем официальные источники и статистика.

Классическое исследование на тему интуитивного знания провели Даниэль Канеман и Амос Тверский. Они дали задание группе студентов: на основании портрета, оценить утверждения с таблицы как более (1 балл) и менее (8 баллов) вероятные (таблица 3).
Портрет выглядел так: «Линда, возраст – немного за 30. Умная, говорит, что думает. В колледже изучала философию. Тогда же выступала против социального неравенства, дискриминации и использования ядерного оружия. Не замужем».
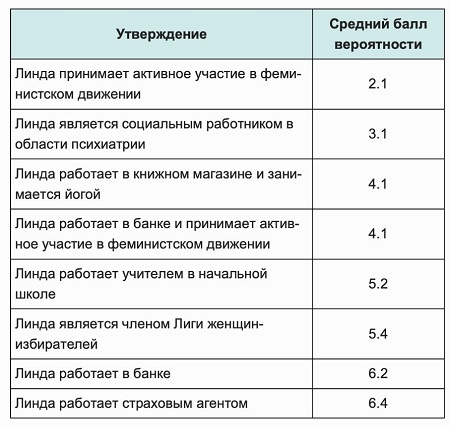
По портрету логично предположить, что Линда участвует в феминистском движении. Но студенты принимали решения интуитивно, что привело к ошибке. Вероятность, что Линда работает в банке и принимает участие в феминистском движении больше вероятности работы в банке.
Посмотрите на таблицу: вероятность работы в банке и увлечение феминистским движением – 4,1 балл. Но первое (работа в банке) и второе (феминистское движение) в сумме дают 8,3 балла. Согласно терверу, вероятность, что произойдут оба события не может быть выше, чем вероятность каждого события по отдельности. Главное утверждение (4,1 балла) содержит 2 события и является единым. В интуитивном решения правило тервера нарушено. Это доказывает — наши убеждения часто являются ложными.
В дальнейшем проводились множественные эксперименты, которые подтвердили догадку Канемана.
Вместо заключения
Теория вероятностей почти всегда разбивается о «случай», продиктованный убеждением или эмоцией отдельного человека. Поэтому использование ее в повседневной жизни может не оправдать ожиданий. Но выбирать вам! Хорошего дня!
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.
Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом
.
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом
.
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
- Вероятность принимает значения на отрезке от 0 до 1, т.е.
.
- Вероятность невозможного события равна 0, т.е.
.
- Вероятность достоверного события равна 1, т.e.
.
- Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.
.
Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные
из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле
. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов
.
Ответ получаем по формуле .
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков – 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А – это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
Ответ: 0,4
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.
.
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае
.
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается “шесть факториал”.
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае
.
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
В нашем случае .
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из
элементов по
элементам:
В нашем случае .
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
Ответ: 0,98.
Задача 3.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Решение:
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие “У. верно решит ровно 9 задач” входит в условие “У. верно решит больше 8 задач”, но не относится к условию “У. верно решит больше 9 задач”.
Однако, условие “У. верно решит больше 9 задач” содержится в условии “У. верно решит больше 8 задач”. Таким образом, если мы обозначим события: “У. верно решит ровно 9 задач” – через А, “У. верно решит больше 8 задач” – через B, “У. верно решит больше 9 задач” через С. То решение будет выглядеть следующим образом:
.
Ответ: 0,06.
Задача 4.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме “Тригонометрия”, либо к теме “Внешние углы”. По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
Ответ: 0,35.
Задача 5.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: – лампочка горит,
– лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события “лампочка перегорела”, “лампочка горит”, “лампочка горит”:
, где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно:
.
Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:
Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
❓ Что такое теория вероятностей?
Теория вероятностей использует случайные величины и распределения вероятностей для математической оценки неопределенных ситуаций. Понятие вероятности используется для присвоения числового описания вероятности наступления события. Вероятность можно определить как число благоприятных исходов, деленное на общее число возможных исходов события.
Определение теории вероятностей
Теория вероятностей – это область математики и статистики, которая занимается определением вероятностей, связанных со случайными событиями. Существует два основных подхода к изучению теории вероятностей: теоретический и экспериментальный. Теоретическая вероятность определяется на основе логических рассуждений без проведения экспериментов. В отличие от нее, экспериментальная вероятность определяется на основе исторических данных путем проведения повторных экспериментов.
Пример теории вероятностей
Предположим, нам необходимо определить вероятность выпадения числа 4 при бросании игральной кости. Число благоприятных исходов равно 1. Возможные исходы игральной кости – {1, 2, 3, 4, 5, 6}. Из этого следует, что всего существует 6 исходов. Таким образом, вероятность выпадения 4 при бросании игральной кости, используя теорию вероятности, можно вычислить как 1 / 6 ≈ 0,167.
🎲 Основы теории вероятностей
Мы можем понять эту область математики с помощью нескольких основных терминов, напрямую связанных с теорией вероятностей.
Случайный эксперимент
Случайный эксперимент в теории вероятностей – это испытание, которое повторяется несколько раз для получения четко определенного набора возможных результатов. Подбрасывание монеты является примером случайного эксперимента.
Пространство выборки
Пространство выборки можно определить как множество всех возможных исходов, полученных в результате проведения случайного эксперимента. Например, пространство выборки при подбрасывании симметричной монеты (fair coin), стороны которой – это орел и решка.
Событие
Теория вероятностей определяет событие как набор исходов эксперимента, который образует подмножество пространства выборки.
Примеры событий:
- Независимые – те, на которые не влияют другие события, являются независимыми.
- Зависимые – те, на которые влияют другие события.
- Взаимоисключающие – события, которые не могут произойти в одно и то же время.
- Равновероятные – два или более события, которые имеют одинаковые шансы произойти.
- Исчерпывающие – это события, которые равны выборочному пространству эксперимента.
Случайная величина
В теории вероятностей случайную переменную можно определить как величину, которая принимает значение при всех возможных исходах эксперимента.
Существует два типа случайных величин:
- Дискретная случайная величина – принимает точные значения, такие как 0, 1, 2…. Описывается кумулятивной функцией распределения и функцией массы вероятности.
- Непрерывная случайная величина – переменная, которая может принимать бесконечное число значений. Для определения характеристик этой переменной используются кумулятивная функция распределения и функция плотности вероятности.
Вероятность
Вероятность мы можем определить как численную вероятность наступления события. Вероятность того, что событие произойдет, всегда лежит между 0 и 1. Это связано с тем, что число желаемых исходов никогда не может превысить общее число исходов события. Теоретическая вероятность и эмпирическая вероятность используются в теории вероятностей для измерения шанса наступления события.
Условная вероятность
Ситуация, когда необходимо определить вероятность наступления события, притом что другое событие уже произошло.
Обозначается как P(A | B).
Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», на котором ты:
- Усвоишь специальную терминологию и сможешь читать статьи по Data Science без постоянных обращений к поисковику.
- Подготовишься к успешной сдачи вступительных экзаменов в Школу анализа данных Яндекс.
- Овладеешь математическим аппаратом, который необходим, чтобы стать специалистом в Data Science.
Ожидание
Ожидание случайной величины X можно определить как среднее значение результатов эксперимента, проводимого многократно. Ожидание обозначается как E[X]. Также известно как среднее значение случайной величины.
Дисперсия
Дисперсия – это мера, которая показывает, как распределение случайной величины изменяется относительно среднего значения. Дисперсия определяется как среднее квадратичное отклонение от среднего значения случайной величины. Обозначается как Var[X].
Функция распределения теории вероятностей
Распределение вероятностей или кумулятивная функция распределения – это функция, которая моделирует все возможные значения эксперимента, используя случайную переменную. Распределение Бернулли и биномиальное распределение – это примеры дискретных распределений вероятностей. Например, нормальное распределение представляет собой пример непрерывного распределения.
Массовая функция вероятности
Массовая функция вероятности определяется как вероятность того, что дискретная случайная величина будет в точности равна определенному значению.
Функция плотности вероятности
Функция плотности вероятности – это вероятность того, что непрерывная случайная величина принимает множество возможных значений.
Формулы теории вероятностей
В теории вероятностей существует множество формул, которые помогают рассчитать различные вероятности, связанные с событиями.
Наиболее важные формулы:
- Теоретическая вероятность: Число благоприятных исходов / Число возможных исходов.
- Эмпирическая вероятность: Число случаев, когда событие происходит / Общее число испытаний.
- Правило сложения: P(A ∪ B) = P(A) + P(B) – P(A∩B), где A и B – события.
- Правило комплементарности: P(A’) = 1 – P(A). P(A’) означает вероятность того, что событие не произойдет.
- Независимые события: P(A∩B) = P(A) ⋅ P(B).
- Условная вероятность: P(A | B) = P(A∩B) / P(B).
- Теорема Байеса: P(A | B) = P(B | A) ⋅ P(A) / P(B).
- Массовая функция вероятности: f(x) = P(X = x).
- Функция плотности вероятности: p(x) = p(x) = dF(x) / dx, где F(x) – кумулятивная функция распределения.
- Ожидание непрерывной случайной величины: ∫xf(x)dx, где f(x) является МФВ (Массовой функцией вероятности).
- Ожидание дискретной случайной величины: ∑xp(x), где p(x) – это ФПВ (Функцией плотности вероятности).
- Дисперсия: Var(X) = E[X2] – (E[X])2.
Применение теории вероятностей
Теория вероятностей используется во многих областях и помогает оценить риски, которые связаны с теми или иными решениями. Некоторые из направлений, где применяют теорию вероятностей:
- В финансовой отрасли теория вероятностей используется для создания математических моделей фондового рынка с целью прогнозирования будущих тенденций. Это помогает инвесторам вкладывать средства в наименее рискованные активы, которые дают наилучший доход.
- В потребительской индустрии теория вероятностей используется для снижения вероятности неудачи при разработке продукта.
- Казино использует теорию вероятностей для разработки азартных игр с максимизацией своей прибыли.
🏋️ Практические задания
Задача 1: При бросании двух игральных костей, какова вероятность того, что выпадет комбинация, сумма которой будет равна 8?
При бросании двух игральных костей существует 36 возможных исходов. Для получения суммы, равной 8, существует 5 благоприятных исходов: [(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)]. Используя формулы теории вероятностей: Вероятность = Число благоприятных исходов / общее число возможных исходов = 5 / 36. Ответ: Вероятность получения суммы 8 при бросании двух игральных костей равна 5 / 36.
Задача 2: Какова вероятность вытащить карту королеву из колоды?
Колода карт имеет 4 масти. Каждая масть состоит из 13 карт. Таким образом, общее число возможных исходов = (4) * (13) = 52. Может быть, 4 королевы, по одной из каждой масти. Следовательно, количество благоприятных исходов = 4. Карточная вероятность = 4 / 52 = 1 / 13. Ответ: Вероятность получить королеву из колоды карт равна 1 / 13
Задача 3: Из 10 человек 3 купили карандаши, 5 купили тетради, а 2 купили и карандаши, и тетради. Если покупатель купил тетрадь, какова вероятность того, что он также купил карандаш?
Используя понятие условной вероятности, P(A | B) = P(A∩B) / P(B). Пусть A – событие, когда люди покупают карандаши, а B – событие, когда люди покупают тетради. P(A) = 3 / 10 = 0,3P(B) = 5 / 10 = 0,5P(A∩B) = 2 / 10 = 0,2. Подставим полученные значения в приведенную формулу, P(A | B) = 0,2 / 0,5 = 0,4. Ответ: Вероятность того, что покупатель купил карандаш, при условии, что он купил блокнот, равна 0,4.
В заключение
Подведем итоги:
- Теория вероятностей – это раздел математики, в котором рассматриваются вероятности случайных событий.
- Понятие вероятности объясняет возможность наступления того или иного события.
- Значение вероятности всегда лежит между 0 и 1.
- В теории вероятностей все возможные исходы случайного эксперимента составляют пространство выборки.
- Теория вероятностей использует такие важные понятия, как случайные величины и кумулятивные функции распределения для моделирования случайного события. Сюда же относится определение различных вероятностей, связанных с этим.
Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», который включает в себя:
- 47 видеолекций и 150 практических заданий.
- Консультации с преподавателями курса.
Теория вероятности — подробнее
Что такое вероятность?
Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от ( 1) до ( 6).
Итак, мы бросаем кость и хотим, чтобы выпало ( 5) или ( 6). И нам выпадает ( 5).
В теории вероятностей говорят, что произошло благоприятное событие.
Если бы выпало ( 6), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.
А сколько неблагоприятных?
Раз всего возможных событий ( 6), значит, неблагоприятных из них ( 6-2=4) события (это если выпадет ( 1,text{ }2,text{ }3) или ( 4)).
Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.
То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.
Обозначают вероятность латинской буквой ( p) (видимо, от английского слова probability — вероятность).
Принято измерять вероятность в процентах (см. темы «Дроби, рациональные числа» и «Проценты»).
Для этого значение вероятности нужно умножать на ( 100%).
В примере с игральной костью вероятность ( p=frac{благоприятных}{всего}=frac{2}{6}=frac{1}{3}).
А в процентах: ( p=frac{1}{3}cdot 100%=frac{100}{3}%approx 33,3%).
И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.
Зависимые события
Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой ( 3) двери на выбор.
Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры ( 3), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.
Но каков этот шанс?
Дверей ( 3), нужная дверь ( 1). Вероятность угадать, позвонив в первую дверь: ( frac{1}{3}). То есть один раз из трех ты точно угадаешь.
Мы хотим узнать, позвонив ( 1) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:
1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь
А теперь рассмотрим все варианты, где может находиться друг:
а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью
Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.
Как видишь, всего возможно ( 9) вариантов местоположения друга и твоего выбора, в какую дверь звонить.
А благоприятных исходов всего ( 3). То есть ( 3) раза из ( 9) ты угадаешь, позвонив в дверь ( 1) раз, т.е. ( frac{3}{9}=frac{1}{3}).
Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.
Определение – это и есть формула. Вероятность принято обозначать p, поэтому:
( displaystyle p=frac{text{благоприятных}}{всего})
Такую формулу писать не очень удобно, поэтому примем за ( displaystyle {{N}_{б}}) – количество благоприятных исходов, а за ( N) – общее количество исходов.
( displaystyle p=frac{{{N}_{б}}}{N})
Вероятность можно записывать в процентах, для этого нужно умножить получившийся результат на ( 100%):
( displaystyle p=frac{{{N}_{б}}}{N}cdot 100%)
Наверное, тебе бросилось в глаза слово «исходы».
Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.
Ну а исходы бывают благоприятные и неблагоприятные.
Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?
Если ты подумал, что ( displaystyle frac{1}{3}), то это ошибка. Давай разбираться.
У нас осталось две двери. Таким образом, у нас есть возможные шаги:
1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь
Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):
а. Друг за 1-ой дверью
б. Друг за 2-ой дверью
Давай снова нарисуем таблицу:
Как видишь, всего есть ( 4) варианта, ( 2) из которых – благоприятны. То есть вероятность равна ( displaystyle frac{2}{4}=frac{1}{2}).
А почему не ( displaystyle frac{1}{3})?
Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.
А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?
Правильно, ( 0%).
Но если есть зависимые события, то должны быть и независимые? Верно, бывают.
Правило умножения вероятностей независимых событий
Что такое независимые события ты уже знаешь.
А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?
Можно конечно посчитать, но есть способ проще.
Допустим мы хотим знать, какова вероятность того, что бросая монетку ( 2) раза, мы два раза увидим орла?
Мы уже считали: ( p=0,25).
А если бросаем монетку ( 3) раза? Какова вероятность увидеть орла ( 3) раза подряд?
Всего возможных вариантов ( 8):
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Не знаю, как ты, но я ( 3) раза ошибся, составляя этот список. Ух! А подходит нам только ( 1) вариант (первый).
( displaystyle p=frac{{{N}_{б}}}{N}=frac{1}{8})
Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.
Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.
Другими словами,
Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий
Рассмотрим на примере все той же, злосчастной, монетки.
Вероятность выпадения орла в ( 1) испытании? ( displaystyle frac{1}{2}). Теперь мы бросаем монетку ( 5) раз.
Какова вероятность выпадения ( 5) раз подряд орла?
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{5}}=frac{1}{32})
Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.
Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при ( 3) бросках подряд, мы поступили бы также.
Вероятность выпадения решка – ( displaystyle frac{1}{2}), орла – ( displaystyle frac{1}{2}).
Вероятность выпадения последовательности РЕШКА-ОРЕЛ-РЕШКА-РЕШКА:
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{4}}=frac{1}{16})
Можешь проверить сам, составив таблицу.
Правило сложения вероятностей несовместных событий
Так стоп! Новое определение.
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.
Ряд несовместных событий образуют полную группу событий.
Давай разбираться. Возьмем нашу изношенную монетку и бросим её ( 3) раза. Возможные варианты:
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Так вот, несовместные события – это определенная, заданная последовательность событий. ( 1),text{ }2),text{ }3),text{ }4)ldots text{ }8)) – это несовместные события.
Вероятности несовместных событий складываются.
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности ( 1)) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}=frac{1}{8})
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно ( 1) раз, т.е. варианты ( 4),text{ }6)) и ( 7)), то мы должны сложить вероятности этих последовательностей.
Всего вариантов ( 8), нам подходит ( 3).
( displaystyle p=frac{{{N}_{б}}}{N}=frac{3}{8})
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
( displaystyle p={{p}_{4}}+{{p}_{6}}+{{p}_{7}}=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Правило, помогающее не запутаться, когда умножать, а когда складывать:
Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.
Возвратимся к примеру, когда мы подбросили монетку ( 3) раза, и хотим узнать вероятность увидеть орла ( 1) раз.
Что должно произойти?
Должны выпасть:
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
Вот и получается:
( displaystyle left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})
Давай рассмотрим несколько примеров.





















