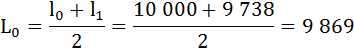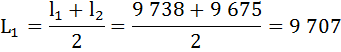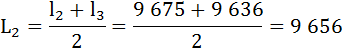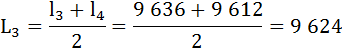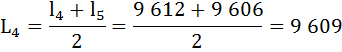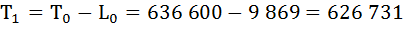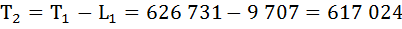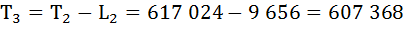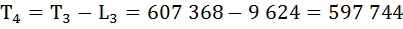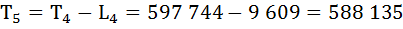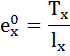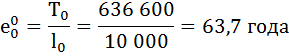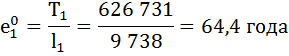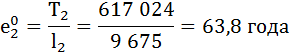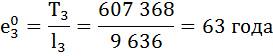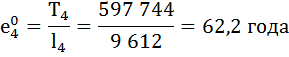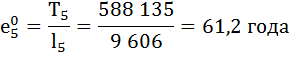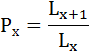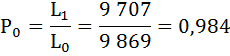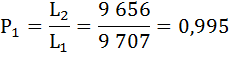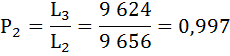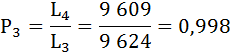Демографические таблицы – один из основных методов анализа демографических процессов. Они бывают общими – для повторяющихся демографических событий, и специальными – для неповторяющихся, а также простыми – для одного демографического процесса, и комбинированными – для нескольких процессов одновременно.
Таблица смертности – простая специальная таблица – числовая модель смертности, представляющая собой систему взаимосвязанных, упорядоченных по возрасту рядов чисел, отражающих процесс вымирания некоторого условного или реального поколения с фиксированной начальной численностью. Идея таблицы смертности впервые появилась в середине XVII века в работе Дж.Граунта (http://www.demoscope.ru/weekly/2006/0261/biblio05.php), современный вид таблицы смертности был рекомендован в конце XIX века Лондонским институтом актуариев.
Для построения таблиц смертности реального поколения необходимо собрать информацию за почти 100-летний период – период жизни одного поколения, она будет отражать закономерности вымирания определенной когорты, но с опозданием. Таблицы смертности для календарного года – это оценки смертности условного поколения. Они оперативно отражают изменения уровня смертности во времени и влияние на смертность особенностей текущего года.
В основу построения таблицы смертности положен принцип стационарного населения (ссылка на главу 13): «закрытое население», в котором отсутствует миграция; число рождений равно числу смертей, неизменная возрастная структура; любая совокупность новорожденных имеет тот же порядок вымирания (возрастные коэффициенты смертности), что и все остальные.
Как и любая демографическая таблица, таблица смертности имеет шкалу. Шкала приведена в первой колонке таблицы и отражает точное число полных лет, прошедших с момента рождения. Начальный возраст в таблице – 0 лет (момент рождения), конечный – w лет (возраст, к которому вымирает вся совокупность родившихся). Первая колонка таблицы – точный возраст х. Это единственная независимая переменная, которая может измеряться в днях, месяцах (при изучении младенческой смертности), но, как правило, измеряется в годах. В зависимости от длины возрастного интервала n выделяют полные (n=1) и краткие (n=5 или n=10) таблицы смертности. В таблице 1 приведен пример краткой таблицы смертности.
Таблица 1. Пример краткой таблицы смертности
| Точный возраст | число доживших до точного возраста х | число умирающих в интервале возраста от х до х+n | вероятность умереть в интервале возраста от x до х+n | вероятность выжить к возрасту х+n для всех тех, кто дожил до возраста х | среднее число человеко-лет, прожитое в интервале возраста от х до х+n теми, кто дожил до начала данного интервала | число человеко-лет жизни в возрасте х лет и старше | ожидаемая продолжительность жизни в точном возрасте х лет |
|---|---|---|---|---|---|---|---|
| х | lх | ndх | nqх | npх | nLх | Tх | Eх |
| 0 | 100000 | 525 | 0,00525 | 0,99475 | 99561 | 6550537 | 65,51 |
| 1 | 99475 | 133 | 0,001337 | 0,998663 | 397588 | 6450976 | 64,85 |
| 5 | 99342 | 93 | 0,000936 | 0,999064 | 496477 | 6053388 | 60,93 |
| 10 | 99249 | 143 | 0,001441 | 0,998559 | 495938 | 5556911 | 55,99 |
| 15 | 99106 | 397 | 0,004006 | 0,995994 | 494703 | 5060973 | 51,07 |
| 20 | 98709 | 722 | 0,007314 | 0,992686 | 491874 | 4566270 | 46,26 |
| 25 | 97987 | 1041 | 0,010624 | 0,989376 | 487542 | 4074396 | 41,58 |
| 30 | 96946 | 1796 | 0,018526 | 0,981474 | 480682 | 3586854 | 37,00 |
| 35 | 95150 | 2871 | 0,030173 | 0,969827 | 469182 | 3106172 | 32,65 |
| 40 | 92279 | 4105 | 0,044485 | 0,955515 | 451638 | 2636990 | 28,58 |
| 45 | 88174 | 5025 | 0,05699 | 0,94301 | 428702 | 2185352 | 24,78 |
| 50 | 83149 | 6185 | 0,074385 | 0,925615 | 401078 | 1756650 | 21,13 |
| 55 | 76964 | 8263 | 0,107362 | 0,892638 | 365235 | 1355572 | 17,61 |
| 60 | 68701 | 10947 | 0,159343 | 0,840657 | 317506 | 990337 | 14,42 |
| 65 | 57754 | 13293 | 0,230166 | 0,769834 | 256357 | 672831 | 11,65 |
| 70 | 44461 | 13955 | 0,313871 | 0,686129 | 187652 | 416474 | 9,37 |
| 75 | 30506 | 12072 | 0,395725 | 0,604275 | 122149 | 228822 | 7,50 |
| 80 | 18434 | 9809 | 0,532115 | 0,467885 | 66172 | 106673 | 5,79 |
| 85 | 8625 | 5506 | 0,638377 | 0,361623 | 27703 | 40501 | 4,70 |
| 90 | 3119 | 2207 | 0,707599 | 0,292401 | 9201 | 12798 | 4,10 |
| 95 | 912 | 493 | 0,54057 | 0,45943 | 2977 | 3597 | 3,94 |
| 100 | 419 | 419 | 1 | 0 | 620 | 620 | 1,48 |
Таблица смертности для календарного года строится на основе возрастных коэффициентов смертности (ссылка на главу 6 про показатели) (m(x) = frac{M(x)}{overline{P}(x) bullet T}), которые рассчитывают как отношение умерших по возрастам за год к среднегодовому населению. Эти коэффициенты смертности преобразуют в вероятности умереть, и после выбора корня таблицы l0 разворачивается вся таблица смертности – это так называемый демографический метод построения таблицы смертности. Численность населения, для которого строится таблица смертности, должна быть достаточно большой, чтобы исключить случайные колебания возрастных коэффициентов.
Первые формулы перехода от возрастных коэффициентов смертности к вероятностям умереть были предложены практически одновременно в середине XIX века У.Фаром и А.Кетле:
({_{n}^{}q}_{x} = frac{2 cdot {_{n}^{}m}_{x}}{2 + {_{n}^{}m}_{x}}) для однолетних возрастных интервалов
({_{n}^{}q}_{x} = frac{2n cdot {_{n}^{}m}_{x}}{2 + n cdot {_{n}^{}m}_{x}}) для n-летних возрастных интервалов.
Эти формулы перехода от возрастных коэффициентов смертности к вероятностям умереть основаны на гипотезе линейного изменения числа смертей в возрастных интервалах.
Формулы для ситуаций, когда гипотеза линейного изменения числа смертей работает плохо
В 1968 году американский демограф Чанг (Chiang) модифицировал эту формулу, введя в нее параметр (a_{x}), который показывает, какую долю возрастного интервала прожили умершие в этом интервале:
(q(x) = frac{n bullet m(x)}{1 + (n — a(x)) bullet m(x)})
Если (a_{x})=0,5, получим формулу Кетле-Фарра.
Для оценки параметра (a_{x}) в возрастном интервале 1-4 года используется эмпирическая формула, предложенная Коулом и Демени (Coale, Demeny, 1983). В таблице П1 приведены результаты оценок на основе этой формулы. Для остальных возрастов можно использовать гипотезу линейности функции дожития.
Таблица П1. Оценки параметра (a_{x} )в возрастном интервале 1-4 года
Мужчины Женщины Значения 1a0 Если 1m0 ≥ 0,107 0,330 0,350 Если 1m0 < 0,107 0,045+2,6841m0 0,053+2,8001m0 Значения 4a1 Если 1m0 ≥ 0,107 0,338 0,340 Если 1m0 < 0,107 0,413-0,7041m0 0,381-0,3801m0 Источник: Preston, Heuveline, Guillot Demography, p. 48. adapted from Coale and Demeny (1983), West modal life tables https://www.gwern.net/docs/statistics/2001-preston-demography.pdf
Часть показателей таблицы смертности рассчитывается для точных возрастов (lx, Ex), остальные – для возрастных интервалов.
lx – число доживших до точного возраста х из начальной численности когорты. Начальная численность когорты (поколения) или корень таблицы l0 обычно принимается равной 100000 человек (но может встречаться 1000, 10000 и даже 1). Корень таблицы задает масштаб расчетов. Ряд чисел доживающих называют функцией дожития. График функции дожития (см. Рис. 1) по мере снижения смертности стремится принять прямоугольную форму, это явление получило название квадратизации функции дожития.
ndx — числа умирающих в интервале возраста от х до (х+n). Сумма значений ndx равна числу родившихся l0.
nqx — вероятность умереть в интервале возраста от x до х+n; nqx=ndx/lx для всех тех, кто дожил до возраста х. Вероятность наступления смерти в возрастном интервале представляет собой усредненный риск смерти, относящийся ко всем членам когорты, дожившим до начала данного интервала.
Чтобы оценить вероятность смерти на первом году жизни, Росстат оценивает так называемый фактор сепарации f на основе числа смертей до 1 года в текущем и предыдущем годах:
(f = frac{M^{t — 1}}{M^{t — 1} + M^{t}})
где (M^{t — 1})— число младенцев, умерших в данном году, но родившихся в предыдущем году, (M^{t})— число младенцев, умерших в данном году и родившихся в данном году.
Вероятность смерти на первом году жизни рассчитывается на основании фактора сепарации, числа родившихся в текущем и предыдущем году и суммарного числа умерших детей до года в текущем году:
(q_{0} = frac{M_{0} bullet (1 — f)}{N_{t}} + frac{M_{0} bullet f}{N_{t — 1}})
где (N_{t} )и (N_{t — 1} )— числа родившихся в текущем и предыдущем годах, (M_{0})— число детей, умерших в текущем году в возрасте до 1 года, f — фактор сепарации.
В последнем возрастном интервале вероятность умереть приравнивается к 1.
npx – вероятность выжить к возрасту х+n для всех тех, кто дожил до возраста х; nqx+npx = 1.
nLx – среднее число человеко-лет, прожитое в интервале возраста от х до х+n теми, кто дожил до начала данного интервала (lx). Приближенно, при использовании гипотезы равномерного распределения смертей в возрастном интервале, этот показатель рассчитывается как полусумма чисел доживающих до начала и конца возрастного интервала, умноженная на длину возрастного интервала n. Эта гипотеза будет слишком грубой для детских и старших возрастов, где число смертей как правило смещено к началу возрастного интервала.
Согласно методике Росстата, в возрастном интервале от 0 до 1 года число человеко-лет рассчитывается по формуле:
(L_{0} = f bullet l_{0} + (1 — f) bullet l_{1})
Если в последней возрастной группе значение коэффициента смертности оказывается ниже коэффициента смертности в предыдущей возрастной группе, то значение Lω рассчитывается по формуле:
(L_{w} = frac{l_{w}}{2})
Тх – число человеко-лет жизни в возрасте х лет и старше, Tx=Lx+Lx+n+…+Lw.
Еx – ожидаемая продолжительность жизни в точном возрасте х лет, ее можно оценить на основе одной из формул. Формула (2) подразумевает линейное распределение смертей в возрастных интервалах.
(Е_{х} = frac{Т_{х}}{l_{x}} = frac{sum_{x}^{w}{_{n}^{}L}_{x}}{l_{x}}) (1) или (Е_{х} = frac{Т_{х}}{l_{x}} = frac{sum_{x}^{w}{{_{n}^{}d}_{x}(x + frac{n}{2})}}{l_{x}}) (2)
На рис. 1 приведены графики основных функций таблицы смертности.
Рис. 1. Графики функций таблицы смертности (слева направо и сверху вниз): числа доживающих, числа умерших, вероятность умереть, ожидаемая продолжительность жизни
Для оценки уровня смертности чаще всего пользуются важнейшей интегральной характеристикой смертности населения – ожидаемой продолжительностью жизни при рождении Е0. Этот показатель отражает число лет, которое в среднем предстоит прожить новорожденному при условии, что на протяжении всей жизни этого поколения возрастные уровни смертности останутся такими же, как в году, для которого рассчитан данный показатель. Е0 зависит только от распределения возрастных коэффициентов смертности и не может интерпретироваться как средний возраст смерти населения в данном году, который, в свою очередь, зависит еще и от возрастной структуры населения.
Например, в 2021 году ожидаемая продолжительность жизни при рождении у мужчин в России составила 65,51 года. Это означает, что новорожденные 2021 года в среднем проживут 60,51 года, но только при условии, что таблица смертности 2021 года на протяжении их жизни останется неизменной.
Когда число умирающих на первом году жизни достаточно велико, может проявиться так называемый парадокс младенческой смертности, при котором Е1›Е0. В настоящее время в большинстве экономически развитых стран этот парадокс отсутствует из-за низкого уровня младенческой смертности.
Кроме основных показателей, на основе таблицы смертности можно определить:
- отсроченную (интервальную) продолжительность жизни в интервале возраста. Например, отсроченная продолжительность жизни мужчин в трудоспособных возрастах будет рассчитываться по формуле: (frac{T_{15} — T_{65}}{l_{15}}), если за границы трудоспособного возраста принять 15 и 65 лет. На основе этого показателя можно оценить потери ожидаемой продолжительности жизни (в годах) для возрастного контингента на основе текущих характеристик смертности.
- медианную продолжительность жизни – возраст, к которому в живых остается ровно половина исходной численности поколения (0,5 bullet l(0)).
- модальную продолжительность предстоящей жизни – возраст, в котором умирает большая часть поколения.
Видео G-1-5-1+ Минуты 2.58 – до конца И Видео G-1-5-2+ 15.37-до конца Демографические таблицы. Таблица смертности
- 1
- 2
- 3
- 4
- . . .
- последняя »


Функция «чтения» служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
постоянного населения в течение года приходится 3,98 человека прироста населения в результате миграционного движения.
. Коэффициент миграционного оборота: kмо= П+В/ S͞ *1000 = 2+1/250,7*1000= 11,96 то есть на каждую тысячу человек, постоянно проживающих, приходится 11,96 прибывших в течение года на постоянное жительство, а также выбывших в течение года в другие регионы на постоянное жительство.
. Коэффициент эффективности миграционного оборота: kэф= П-В/П+В*100 = 2-1/2+1*100 = 33% то есть на каждые 100 человек миграционного оборота приходиться 33 человека миграционного сальдо.
. Коэффициент общего прироста численности населения: kоп = kеп + kмс = — 7,98+3,98 = -4 то есть на каждую тысячу человек постоянного населения в течение года, а результате естественного и миграционного движения приходится 4 человека общей убыли. Задача 3 Среднегодовая численность женского населения в фертильном возрастном интервале составила 1850 тыс. чел. Среднегодовая численность всего населения — 6250 тыс. чел. Коэффициент плодовитости равен — 28‰.
Определите:
) число родившихся за год;
) общий коэффициент рождаемости (двумя способами). Решение:
. Определим число родившихся за год: N = Коэффициент плодовитости * (Среднегодовую численность женского населения в фертильном возрасте)/ Среднегодовая численность всего населения).
N= 28* (1850/6250) = 8,28. . Определим общий коэффициент рождаемости: n= N/S͞ *1000 = 8,28/6250*1000 = 1,33 то есть 1000 человек постоянного населения приходится в среднем 1,33 рожденных в течение года детей. F = N/W 15-49 * 1000% = 8,29/1850*1000 = 4,48
Задача 4 По условным данным, приведенным в таблице, рассчитайте недостающие показатели таблицы смертности. Дополните ими исходную таблицу.
|
Возраст, лет |
Число доживающих до данного возраста |
Число умирающих в данном возрасте |
Вероятность умереть в данном возрасте |
Вероятность дожить до следующего возраста |
Число живущих в данном возрасте |
Число человеко-лет предстоящей жизни |
Средняя ожидаемая продолжи тельность жизни |
|
0 |
10000 |
593000 |
|||||
|
1 |
9700 |
||||||
|
2 |
9660 |
||||||
|
3 |
9610 |
Определим число умирающих в данном возрасте по формуле: dx=Ix-Ix + 1 1) dx=10000-9700=300.
2) dx=9700-9660=40.
3) dx=9660-9610=50.
Определим вероятность умереть в данном возрасте: qx= dx/Ix. 1) qx= 300/10000=0,03
) qx=40/9700=0,004
3) qx=50/9660=0,005
Определим вероятность дожить до следующего возраста: px=Ix-1/Ix
1) px= 1-0,03=0,97
) px=1-0,004=0,996
3) px=1-0,005=0,995
Определим число живущих в данном возрасте: Lx=(Ix+Ix+1)/2 ) Lx=(10000+9700)/2=9850
) Lx=(9700+9660)/2=9680
) Lx=(9660+9610)/2=9635
Определим число человеко-лет предстоящей жизни: Tx=Tx-Lx+1 ) Tx=593000-9850=583150
) Tx=583150-9680=573470
3) Tx=573470-9635=563835
Определим среднюю ожидаемую продолжительность предстоящей жизни: ex=Tx/Ix ) ex=593000/10000=59,3
) ex=583150/9700=60,12
) ex=573470/9660=59,37
) ex=563835/9610=58,67
|
Воз раст, лет |
Число доживающих до данного возраста |
Число умирающих в данном возрасте |
Вероятность умереть в данном возрасте |
Вероятность дожить до следующего возраста |
Число живущих в данном возрасте |
Число человеко-лет предстоящей жизни |
- 1
- 2
- 3
- 4
- . . .
- последняя »
Интересная статья: Быстрое написание курсовой работы
Имеются следующие данные о возрастных коэффициентах смертности:
для детей, в возрасте до одного года – 26,2‰ (К0),
для детей, достигших возраста один год – 6,5‰ (К1),
для детей, достигших возраста два года – 4,0‰ (К2),
для детей, достигших возраста три года – 2,5‰ (К3),
для детей, достигших возраста четыре года – 0,6‰ (К4).
Сумма предстоящих человеко-лет жизни для совокупности родившихся (10 тыс. чел.) составляет 636 600.
Составьте таблицу смертности для данных возрастных групп и определите среднюю ожидаемую продолжительность предстоящей жизни для возраста 0, 1, 2, 3 и 4 года.
Решение:
Таблицы смертности и средней продолжительности жизни, таблицы дожития — система взаимосвязанных упорядоченных по возрасту рядов чисел, организованных как описание процесса уменьшения с возрастом под действием смертности некоторого абстрактного поколения с фиксированной начальной численностью, именуемой корнем таблицы.
Макет таблицы смертности имеет вид:
| Возраст, лет | Число доживших до возраста х, лет | Вероятность дожить до следующего возраста | Вероятность смерти в течение года | Число живущих в возрасте х | Предстоящее число чел.-лет жизни | Средняя продолжительность предстоящей жизни | Коэффициент дожития |
|---|---|---|---|---|---|---|---|
| х | lx | px | qx | Lx | Tx | ex0 | Px |
В нашей задаче численность поколения условно равна 10 000 чел.
На основе возрастных коэффициентов смертности можно определить вероятность смерти в течение года для каждого года жизни (qх):
q0 = 0,0262
q1 = 0,0065
q2 = 0,0040
q3 = 0,0025
q4 = 0,0006
Затем определим вероятность дожития от возраста х до возраста х + 1 (рх):
p0 = 1 — q0 = 1 — 0,0262 = 0,9738
p1 = 1 — q1 = 1 — 0,0065 = 0,9935
p2 = 1 — q2 = 1 — 0,0040 = 0,9960
p3 = 1 — q3 = 1 — 0,0025 = 0,9975
p4 = 1 — q4 = 1 — 0,0006 = 0,9994
Теперь рассчитаем число доживающих до возраста х (lx) :
l0 = 10 000 (по условию)
l1 = l0 × p0 = 10 000 × 0,9738 = 9 738
l2 = l1 × p1 = 9 738 × 0,9935 = 9 675
l3 = l2 × p2 = 9 675 × 0,9960 = 9 636
l4 = l3 × p3 = 9 636 × 0,9975 = 9 612
l5 = l4 × p4 = 9 612 × 0,9994 = 9 606
Найдём число живущих в возрасте х лет (Lх), представляющее собой среднюю арифметическую из числа доживающих до возраста х и до возраста х + 1:
Определим число предстоящих человеко-лет жизни (Тх) для разных возрастов.
По условию задания
Т0 = 636 600
Рассчитаем среднюю продолжительность предстоящей жизни населения по формуле:
Коэффициент передвижки Px – вероятность для индивидуума в интервале возраста от х до х+1 прожить 1 год и попасть в интервал от х+1 до х+2 – определяется по формуле:
Полученные результаты занесём в таблицу:
| х | lx | px | qx | Lx | Tx | e0x | Px |
|---|---|---|---|---|---|---|---|
| 0 | 10 000 | 0,9738 | 0,0262 | 9 869 | 636 600 | 63,7 | 0,984 |
| 1 | 9 738 | 0,9935 | 0,0065 | 9 707 | 626 731 | 64,4 | 0,995 |
| 2 | 9 675 | 0,9960 | 0,0040 | 9 656 | 617 024 | 63,8 | 0,997 |
| 3 | 9 636 | 0,9975 | 0,0025 | 9 624 | 607 368 | 63 | 0,998 |
| 4 | 9 612 | 0,9994 | 0,0006 | 9 609 | 597 744 | 62,2 | — |
| 5 | — | — | — | — | 588 135 | 61,2 | — |
| — | — | — | — | — | — | — | — |
| 100 | — | — | — | — | — | — | — |
| 636 600 |
Условие задачи взято из: Социально-экономическая статистика: Практикум/Под ред. В. Н. Салина, Е. П. Шпаковской: Учеб. пособие. — М.:Финансы и статистика, 2003. — 192 с.