Как найти число целых решений уравнения - Исправление недочетов и поиск решений вместе с Examum.ru

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.

Общая форма интересующего нас уравнения:

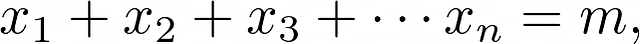
где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

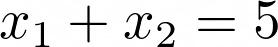
Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

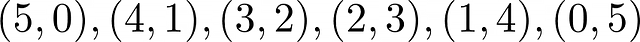
Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

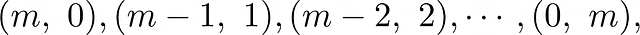
и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

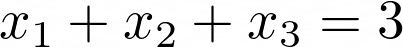
С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

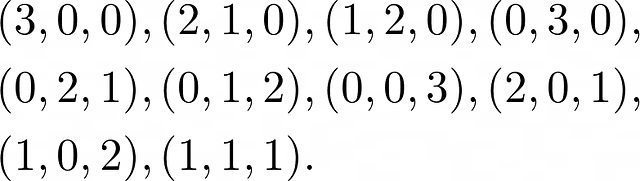
Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

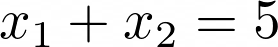
Одним из решений было (5, 0). Давайте преобразуем его в:

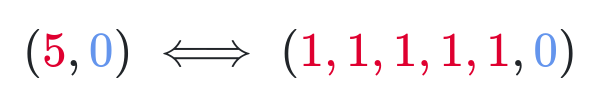
Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

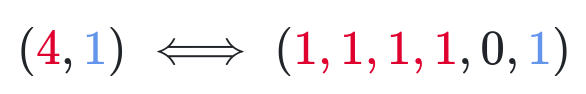
Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

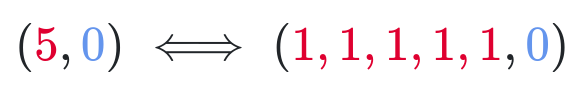
Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

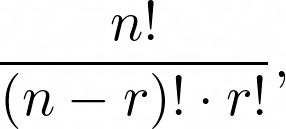
где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

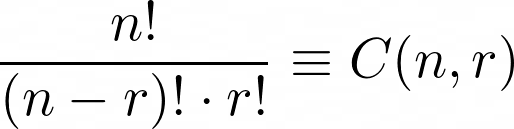
Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

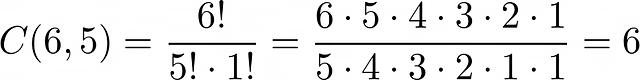
Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

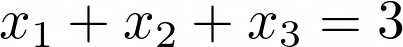
Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

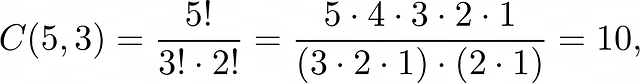
И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

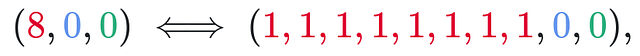
а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

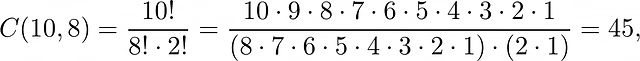
как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

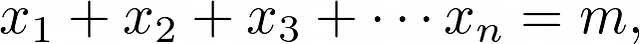
Простейшее решение этого уравнения:

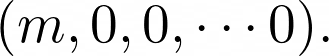
Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

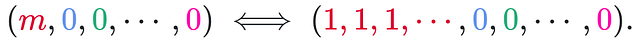
В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:

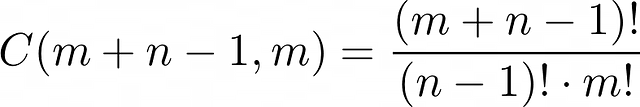
Это наш конечный результат.

Originally published at https://physicsgarage.com on April 26, 2020.

Z	$ 5^{z} $	Остаток при делении на 4
1	5	1
2	25	1
3	125	1
4	625	1

Z	$ 3^{x} $	Остаток при делении на 4
1	3	3
2	9	1
3	27	3
4	81	1
5	243	3

Z	$ 5^{z} $	Остаток при делении на 3
1	5	2
2	25	1
3	125	2
4	625	1

Z	$ 4^{y} $	Остаток при делении на 3
1	4	1
2	16	1
3	64	1
4	256	1
5	1024	1

m	$ 5^{m} $	y	$ 2^{y} $
0	1	0	1
1	5	1	2
2	25	2	4
3	125	3	8

Метод подсчёта количества решений

Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

Число решений в этом случае равно 10.

Значит, нужен эффективный метод.

Разрабатываем метод

Одним из решений было (5, 0). Давайте преобразуем его в:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Это то же самое число, что мы получили методом прямого счёта!

Некоторые решения можно записать в разложенном виде:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Простейшее решение этого уравнения:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Линейные диофантовы уравнения с двумя переменными

Калькулятор решает линейные диофантовы уравнения с двумя переменными.

Сначала калькулятор, теория под ним.

Линейные диофантовы уравнения с двумя переменными

Диофантово уравнение с двумя неизвестными имеет вид:

где a, b, c — заданные целые числа, x и y — неизвестные целые числа.

Для нахождения решений уравнения используется Расширенный алгоритм Евклида (исключая вырожденный случай, когда a = b = 0 и уравнение имеет либо бесконечно много решений, либо же не имеет решений вовсе).
Если числа a и b неотрицательны, тогда с помощью расширенного алгоритма Евклида мы можем найти их наибольший общий делитель g, а также такие коэффициенты и , что:
.

Утверждается, что если число c делится на g, то диофантово уравнение имеет решение; в противном случае диофантово уравнение решений не имеет. Это следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.

То есть если c делится на g, тогда выполняется соотношение:

т. е. одним из решений диофантова уравнения являются числа:

Если одно из чисел a и b или они оба отрицательны, то можно взять их по модулю и применить к ним алгоритм Евклида, как было описано выше, а затем изменить знак найденных коэффициентов и в соответствии с настоящим знаком чисел a и b соответственно.

Если мы знаем одно из решений, мы можем получить выражение для всех остальных решений, которых бесконечное множество.

Итак, пусть g = НОД (a,b), выполняется условие:
.

Тогда, прибавив к число и одновременно отняв от , мы не нарушим равенства:

Этот процесс можно повторять сколько угодно, т. е. все числа вида:

,
где k принадлежит множеству целых чисел, являются множеством всех решений диофантова уравнения.

источники:

http://math4school.ru/uravnenija_v_celih_chislah.html

http://planetcalc.ru/3303/

Источник

Алгебра и начала математического анализа, 10 класс

Урок №9. Решение уравнений в целых числах.

Перечень вопросов, рассматриваемых в теме

понятие диофантовых уравнений;
теоремы для решения уравнений в целых числах;
основные методы решения уравнений в целых числах.

Глоссарий по теме

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) — многочлен с целыми коэффициентами.

Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = + bt, у = -at, где — целое решение уравнения ах + bу = 1,

t – любое целое число.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017. Шабунин М.И., Ткачева М.В., Федорова Н.Е.

Теоретический материал для самостоятельного изучения

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами много занимались самые выдающиеся математики древности, например, греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.

Решение уравнений в целых числах является важной задачей и для современной математики. Теоретический интерес уравнений в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

Ещё в начальной школе на уроках математики перед нами часто ставили задачу выяснить, при каких допустимых значениях буквы обе части того или иного равенства принимают одинаковые числовые значения. На равенство в этом случае мы смотрели как на уравнение относительно указанной неизвестной величины. В восьмом классе мы познакомились с решением квадратных уравнений с одной переменной. Но, готовясь к олимпиадам, рассматривая контрольно- измерительные материалы Единого государственного экзамена встречаемся с заданиями, в которых предлагали уравнения с двумя переменными.

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) — многочлен с целыми коэффициентами.

Применение теории делимости к решению неопределенных уравнений в целых числах.

Для решения в целых числах уравнения вида ах + by = c, где а, b, c – целые числа, отличные от нуля, приведем ряд теоретических положений, которые позволят установить правило решения. Эти положения основаны также на уже известных фактах теории делимости.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)

Доказательство теоремы основано на использовании равенства алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (наибольший общий делитель выражается через неполные частные и остатки, начиная с последнего равенства в алгоритме Евклида).

Пример.

Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.

Решение.

1. Составим равенства алгоритма Евклида:

1672 = 1232 ∙1 + 440,

1232 = 440 ∙ 2 + 352,

440 = 352 ∙ 1 + 88,

352 = 88 ∙ 4, т.е. (1672,352) = 88.

2) Выразим 88 последовательно через неполные частные и остатки, используя полученные выше равенства, начиная с конца:

88 = 440 — 352∙1 = (1672 — 1232) — (1232 — 1672∙2 + 1232∙2) = 1672∙3 — 1232∙4, т.е. 88 = 1672∙3 + 1232∙(-4).

Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + bу = 1, если НОД (а, в) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и в.

Пример.

Найти целое решение уравнения 15х + 37у = 1.

Решение.

1. 37 = 15 ∙ 2 + 7,

15 = 7 ∙ 2 + 1.

2. 1 = 15 — 7∙2 = 15 — (37 — 15∙2) ∙2 = 15∙5 + 37∙(-2),

т.е. — решение данного уравнения.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Для доказательства теоремы достаточно предположить противное.

Пример.

Найти целое решение уравнения 16х — 34у = 7.

Решение.

(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = х₀с + bt, у = y₀c-at, где х₀, y₀ — целое решение уравнения ах + bу = 1,

t – любое целое число.

При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.

Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах+ bу = с НОД(а, b) = 1:

Находится целое решение уравнения ах + bу = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
Составляется общая формула целых решений данного уравнения х = х₀с + bt, у = y₀c — at, где х₀, y₀ — целое решение уравнения ах + bу = 1, t – любое целое число.

Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т.д.

Пример.

Найти целые решения уравнения 407х — 2816у = 33.

Решение.

1. Упрощаем данное уравнение, приводя его к виду 37х — 256у = 3.

2.Решаем уравнение 37х — 256у = 1.

256 = 37∙ 6 + 34,

37 = 34 ∙1 + 3,

34 = 3 ∙11 + 1.

1 = 34 — 3∙11 = 256 — 37∙6 — 11 (37 – 256 + 37∙6) = 256∙12 — 37∙83 =

= 37∙(-83) — 256∙(-12),

т.е. х₀= -83, y₀= -12.

3. Общий вид всех целых решений данного уравнения:

х = -83∙3 — 256t = -249 — 256t,

у = -12∙3 — 37 t = -36 — 37 t.

Положив t = -1, получим х₁= 7, у₁= 1 и общие формулы решений примут вид: х = 7 — 256t, у = 1-37t.

2. Метод полного перебора всех возможных значений переменных,

входящих в уравнение.

Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.

Решение:

Выразим из уравнения переменную х через у , так как х и у – натуральные числа, то

602 — 51у ≥ 49,

51у≤553,

Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.

Ответ: (5;7).

3. Решение уравнений методом разложения на множители.

Диофант наряду с линейными уравнениями рассматривал квадратные и кубические неопределенные уравнения. Решение их, как правило, сложно.

Рассмотрим такой случай, когда в уравнениях можно применить формулу разности квадратов или другой способ разложения на множители.

Решить уравнение в целых числах: х²+ 23 = у²

Решение:

Перепишем уравнение в виде: у²— х²= 23, (у — х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

; ; ; ;

Решая полученные системы, находим:

; ;;;

Ответ: (-11;12);(11;12);(11;-12);(-11;-12).

4. Выражение одной переменной через другую и выделение целой части дроби.

Решить уравнение в целых числах: х²+ ху – у – 2 = 0.

Решение:

Выразим из данного уравнения у через х:

у(х — 1) =2 — х²,

Так как х, у – целые числа, то дробь должна быть целым числом.

Это возможно, если х – 1 =

; ;

Ответ: (0; -2); (2; -2).

5. Методы, основанные на выделении полного квадрата.

Найдите все целочисленные решения уравнения: х²— 6ху + 13у²= 29.

Решение:

Преобразуем левую часть уравнения, выделив полные квадраты,

х²— 6ху + 13у²= (х²— 6ху + 9у²) + 4у²= (х — 3у)²+ (2у)²= 29, значит (2у)² 29.

Получаем, что у может быть равен .

1. у = 0, (х — 0)²= 29. Не имеет решений в целых числах.

2. у = -1, (х + 3)²+ 4 =29, (х + 3)²= 25, х + 3 = 5 или х + 3 = -5

х=2 х=-8

3. у = 1, (х — 3)²+4 =29,

(х — 3)²=25, х – 3 = 5 или х – 3 = -5

х = 8 х = -2

4. у = -2, (х + 6)²+ 16 = 29, (х + 6)²= 13. Нет решений в целых числах.

5. у=2, (х-6)²+16=29, (х-6)²=13. Нет решений в целых числах.

Ответ: (2; -1); (-8; -1); (8; 1); (-2; 1).

6. Решение уравнений с двумя переменными как квадратных

относительно одной из переменных.

Решить уравнение в целых числах: 5х²+5у²+8ху+2у-2х+2=0.

Решение:

Рассмотрим уравнение как квадратное относительно х:

5х²+ (8у — 2)х + 5у²+ 2у + 2 = 0

D = (8у — 2)²— 4·5(5у²+ 2у + 2) = 64у²— 32у + 4 = -100у²— 40у – 40= = -36(у²+ 2у + 1) = -36(у + 1)²

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1)²= 0. Это возможно при у = -1, тогда х = 1.

Ответ: (1; -1).

7. Оценка выражений, входящих в уравнение.

Решить в целых числах уравнение:

(х²+ 4)(у²+ 1) = 8ху

Решение:

Заметим, что если – решение уравнения, то – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Ответ: (2; 1); (-2; -1)

8.Примеры уравнений второй степени с тремя неизвестными.

Рассмотрим уравнение второй степени с тремя неизвестными: х²+ у²= z².

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т.е. прямоугольник треугольников, у которых и катеты х,у и гипотенуза z выражаются целыми числами.

По формуле х = uv, , где u и v – нечетные взаимно простые числа (u > v > 0) можно найти те решения уравнения х²+ у²= z², в которых числа х,у и z не имеют общих делителей (т.е. взаимно простые).

Для начальных значений u и v формулы приводят к следующим часто встречающимся равенствам:

3²+ 4²= 5²(u = 1, v = 3), 5²+ 12²= 13²(u = 1, v = 5), 15²+ 8²= 17²(u = 3, v = 5)

Все остальные целые положительные решения этого уравнения получаются умножением решений, содержащихся в формулах, на произвольный общий множитель а.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка

Решите уравнение 9х+22у-1=0

Выпадающий список:

(-5; 2)
(5; 2)
(-5; -2)
(5; -2)

Решение: Решим данное уравнение, воспользовавшись теоремой 2:

1. 22 = 9 ∙ 2 + 4,

9 = 4 ∙ 2 + 1.

2. 1 = 9 — 4∙2 = 9 — (22 — 9∙2) ∙2 = 9∙5 + 22∙(-2),

т.е. х₀= 5, у₀= -2 — решение данного уравнения

Ответ: 4. (5; -2)

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите целое решение уравнения 3х+9у=3

х=____

у=____

Решение: Решим данное уравнение: 3х+9у=3

Разделим обе части уравнения на 3, получим:

х+3у=1

3 = 1 ∙ 2 + 1
1 = 3 — 1∙2, т.е. х₀= 1, у₀= 0 — решение данного уравнения

Ответ: х= 1, у= 0.

Источник

§ 7 Неопределенные
(диофантовы) уравнения.

Неопределенные
уравнения – уравнения, содержащие более
одного неизвестного. Под одним решением
неопределенного уравнения понимается
совокупность значения неизвестных,
которая обращает данное уравнение в
верное равенство.

В данном параграфе
будут рассмотрены задачи, связанные с
нахождением только целых решений
неопределенного уравнения. При этом
будут рассмотрены как уравнения первой
степени с двумя неизвестными, так и
уравнения степени выше первой и с
количеством неизвестных два и более.
Для решения уравнений второго типа,
имеющихся в этом параграфе, оказывается
достаточным использовать известные
факты о делимости целых чисел.

Определение
1.
Диофантовым
уравнением
1-й степени с n
неизвестными называется уравнение вида

,
(1)

Где все коэффициенты
и неизвестные – целые числа и хотя бы
одно
.

Определение
2. Решением
диофантова уравнения
(1) называется комплекс целых чисел
,
удовлетворяющий этому уравнению.

Теорема
1. При
взаимно простых коэффициентах и при
b=1
диофантово уравнение (1) имеет решение
в целых числах.

Пусть
.
Диофантово уравнение (1) имеет решение
тогда и только тогда, когда
.
Число решений такого уравнения равно
либо нулю, либо бесконечности.

Для решения в
целых числах уравнения
(2),
где

— целые числа, отличные от нуля, приведем
ряд теоретических положений, которые
позволят установить правило решения.
Эти положения основаны также на уже
известных фактах теории делимости.

Теорема
2.
Если
,
то существуют такие целые числа x
и y,
что имеет место равенство
(3).

Это равенство
называется линейной комбинацией или
линейным представлением наибольшего
общего делителя двух чисел через сами
эти числа. Доказательство теоремы
основано на использовании равенств
алгоритма Евклида для нахождения
наибольшего общего делителя двух чисел
(наибольший общий делитель данных чисел
выражается через неполные частные и
остатки, начиная с последнего равенства
в алгоритме Евклида).

Теорема
3.
Если в
уравнении

(4)
,
то уравнение (4) имеет, по крайней мере,
одно целое решение.

Справедливость
этой теоремы следует из теоремы 2. Таким
образом, чтобы найти одно целое решение
уравнения (4), если
,
достаточно представить число 1 в виде
линейной комбинации чисел a
и b.

Теорема
4.
Если в
уравнении

(5)

и c
не делится на d,
то уравнение целых решений не имеет.

Для доказательства
теоремы достаточно предположить
противное.

Теорема
5.
Если в уравнении

(6)

и ,
то оно равносильно уравнению

(6’), в котором
.

При доказательстве
теоремы следует показать, что произвольное
целое решение первого уравнения является
также решением второго уравнения и
обратно.

Теорема
6.
Если пара
целых чисел
,

удовлетворяет уравнению

(6) , где

— целые числа, отличные от нуля и
,
то

,
,
(7)

где t
– произвольное целое число, является
общим решением этого уравнения в целых
числах.

Доказательство.
По условию теоремы

(8) Вычитая почленно из уравнения (6)
равенство (8), получим уравнение

, (9)

равносильное
уравнению (6). Покажем, что формулы (7)
задают множество всех целых решений
уравнения (9), а, следовательно, и уравнения
(6). Очевидно, что каждая пара целых чисел,
заданная формулами (7) , удовлетворяет
уравнению (9). Наоборот, если пара целых
чисел
,

удовлетворяет уравнению (9), то есть

,то
.
Отсюда, поскольку
,
вытекает, что
,
то есть
,
аналогично, доказывается, что
,
где t
– некоторое целое число. Следовательно,
каждая пара целых чисел
,

удовлетворяющая уравнению (9), задается
формулами (7). Что и требовалось доказать.

Таким образом,
чтобы решить уравнение (6) в целых числах,
надо найти какое-нибудь частное решение

этого уравнения или частное решение

уравнения (4) и умножит это решение на
c,
получим частное решение уравнения (6).

Сделать это можно,
либо через нахождение линейной комбинации
НОД двух целых чисел, либо с помощью
конечных цепных дробей, воспользовавшись
разложением числа

в цепную дробь.

Теорема
7. Общее
решение в целых числах уравнения

(6) ,где

— целые числа, отличные от нуля и
,
можно представить в виде

,
,
(10)

где t
– произвольное целое число, а

и

— числитель и знаменатель предпоследней
подходящей дроби разложения числа

в цепную дробь.

Доказательство.
Пусть
=

— разложение числа

в цепную дробь, а

(s=1,2,…,n)
– подходящие дроби этого разложения.
Тогда
=.
По условию дробь

— несократимая и дробь

также несократимая, поэтому
,
.
По свойству подходящих дробей
,
то есть
.
Умножив обе части последнего равенства
на
,
получим равенство
.
Это равенство означает, что пара чисел

и

является целым решением уравнения (6).

Примеры.
1. Найти
целые решения уравнения
.

Решение. Упрощаем
данное уравнение, приводя его к виду
.
Решаем уравнение
.
256=37·6+34, 37=34·1+3, 34=3·11+1. 1=34 – 3·11= 256 – 37∙6
– 11(37 – 256 + 37∙6) = 256∙12 – 37∙83 =

= 37∙(-83) – 256∙(-12),
то есть
.
Общий вид всех целых решений данного
уравнения:

2.Транспортной
организации, имеющей грузовые автомашины
грузоподъемностью 3,5 и 4,5 т, предложено
перевезти 53т груза. Определить, сколько
грузовых автомашин того и другого типа
должен выделить диспетчер для перевозки
указанного груза одним рейсом при
условии полного использования
грузоподъемности всех выделенных
автомашин.

Решение. Пусть x,y
– число выделенных машин грузоподъемностью
соответственно 3,5 и 4.5т. для получения
ответа нужно решить уравнение

то есть

в целых числах с учетом того, что
.
Разложив дробь

в цепную дробь, будем иметь
.
Подсчитаем подходящие дроби :
.
Предпоследней подходящей дробью является
.
Следовательно, по формулам общим решением
в целых числах заданного уравнения
является:
,
где t
– любое целое число. Теперь из всех
решений выберем неотрицательные:.
Учитывая, что t
– целое число, получим:

или
,
то есть

или
.

Упражнения.

№ 1. Решите в целых
числах уравнения (6), где

a	b	c	a	b	c
143	169	5	237	44	1
275	145	10	439	118	3
1256	847	119	3	8	5
2	5	7	42	31	67
23	49	53	5	28	59
12	7	41	9	17	105
35	-37	12	4	-14	7
7	-12	15	12	-7	29
8	-13	63	7	-19	23
39	-22	10	43	37	21
122	129	2	258	-172	56
3	4	13	26	34	13
45	-37	25	17	-25	117
81	-48	33	53	47	11

№ 2. При каких целых
числах выражение

равно такому целому положительному
числу, при делении которого на 4 получается
остаток, равный 3?

№ 3. Найдите общий
вид чисел, кратных 8, которые при делении
на 5 дают о в остатке 3.

№ 4. Разложите
число 150 на два положительных слагаемых,
одно их которых кратно 11, а второе – 17.

№ 5. Из имеющихся
резисторов сопротивлением по 1,2 и 1,7 Ом
требуется составить последовательным
соединением цепь сопротивлением 11,1 Ом.
Сколько резисторов того и другого типа
потребуется?

№ 6. Сколькими
способами можно уплатить 200 руб., имея
денежные купюры по 3 и 5 руб.?

№ 7. Решить уравнения:

преобразованием
в произведение
,
методом проб (в
натуральных числах)
,
доказательством
от противного
,
методом единственности

,
переходом от
частного случая к общему
(1990
знаков корня).

№ 8. Решить
неопределенные уравнения:

,
2)

3)
,
4)
,

5),
6)
,

7)
,

где

— четное число,

9),

10)
,

11)
,
где

— данное простое число,

12)
,

13)
,

14)
,

15)
,

16)
,

17)
.

№ 9. Решить в
натуральных числах уравнения:

1).
,
2).
,
3).
,

4).
,
5).
,

6).
,
7).
.

№ 10. Найдите
наименьшее
,
при котором

а) уравнение

имело бы ровно 6 целых положительных
решений;

б) уравнение

имело бы ровно 5 целых положительных
решений.

№ 11. В каких
пределах должно заключаться c,
чтобы уравнение

имело бы 6 целых положительных решений?

№ 12. Пусть

и

— натуральные взаимно простые числа.
Рассмотрим точки плоскости с целыми
координатами
,
лежащие в полосе
.
Каждой такой точке припишем целое число
.

а) Докажите, что
для каждого натурального
существует
ровно одна точка

,
что
.

б) Теорема Сильвестра.
Докажите, что наибольшее
,
для которого уравнение

не имеет решений в целых неотрицательных
числах, имеет вид
.

№13٭
Пусть числа

и

взаимно просты. Докажите, что для того,
чтобы уравнение

имело ровно

целых положительных решений, значение

должно находиться в пределах
.

№14٭
Отметим на
прямой красным цветом все точки вида
,
где

и

— натуральные, и синим цветом – остальные
целые точки. Найдите на прямой такую
точку, что любые симметричные относительно
нее целые точки закрашены в разные
цвета. Объясните, почему такая точка
существует.

№15٭
(Гильберт Д.)
Всегда ли разрешимо в простых числах

и

уравнение
,
где

и
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник