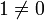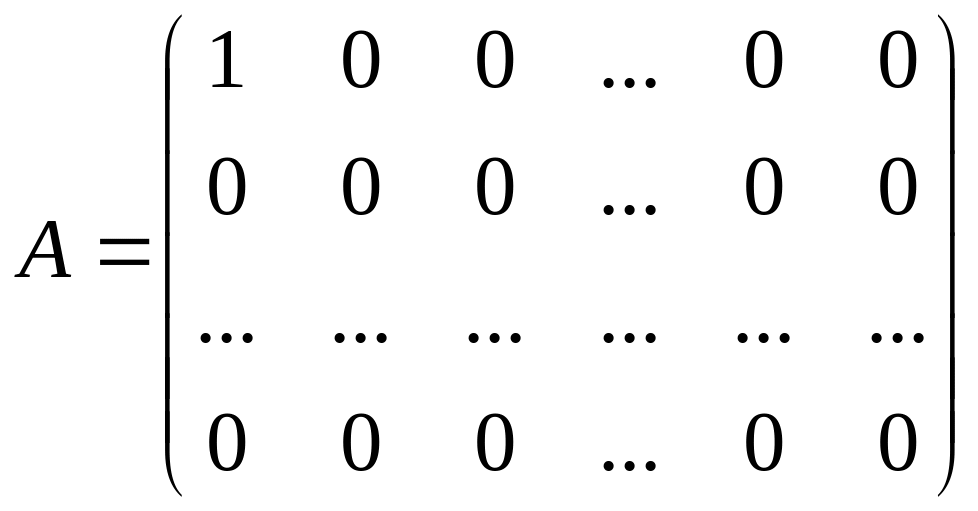Как найти число делителей нуля

Делители нуля

В абстрактной алгебре, ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.

Правый делитель нуля определяется аналогично: ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.

Элемент, который является и правым и левым делителем нуля одновременно называется делителем нуля. Если умножение в кольце коммутативно тогда правые и левые делители совпадают. Ненулевые элементы кольца, которые не являются ни правыми, ни левыми делителями нуля называются обычными элементами.

Пример: в кольце элементы 2, 3, 4 — делители нуля.

1neq 0

Ассоциативное и коммутативное кольцо с единицей без делителей нуля называется областью целостности.

Внешние ссылки

А. В. Михалев, А. А. МихалевВведение в алгебру

Wikimedia Foundation . 2010 .

Смотреть что такое «Делители нуля» в других словарях:

Делитель нуля — В абстрактной алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0. Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0 … Википедия

АЛГЕБРА АБСТРАКТНАЯ — (общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых… … Энциклопедия Кольера

НЕАССОЦИАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — множества с доумя бинарными операциями + и ., удовлетворяющими всем аксиомам ассоциативных колец и алгебр, кроме, быть может, аксиомы ассоциативности умножения. Первые примеры неассоциативных колец (Н. к.) и неассоциативных алгебр (Н. а.), не… … Математическая энциклопедия

ДВОЙНЫЕ И ДУАЛЬНЫЕ ЧИСЛА — гиперкомплексные числа вида a+bе, где аи b действительные числа, и для двойных чисел е 2= + 1, а для дуальных чисел е 2=0. Сложение Д. и д. ч. определяется формулой Умножение двойных чисел производится по формуле а дуальных чисел по формуле… … Математическая энциклопедия

Двойные числа — О гиперкомплексных числах параболического типа см. дуальные числа Двойные числа или паракомплексные числа, расщепляемые комплексные числа, комплексные числа гиперболического типа гиперкомплексные числа вида « », где и вещественные… … Википедия

Процедура Кэли — Диксона (процедура удвоения) это рекурсивная процедура построения алгебр над полем вещественных чисел, с удвоением размерности на каждом шагу. Названа в честь Артура Кэли и Леонарда Диксона. Эта процедура позволяет построить комплексные числа,… … Википедия

АЛЬТЕРНАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — Альтернативным кольцом (А. к.) наз. кольцо, в к ром каждые два элемента порождают ассоциативное подкольцо; альтернативной алгеброй (А. а.) наз. линейная алгебра, являющаяся А. к. Согласно теореме Артина класс всех А. к. задается системой тождеств … Математическая энциклопедия

АССОЦИАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — кольца и алгебры с ассоциативным умножением, т. е. множества с двумя бинарными операциями сложением + и умножением Х, являющиеся абелевой группой по сложению и полугруппой по умножению, причем умножение дистрибутивно (слева и справа) относительно … Математическая энциклопедия

ВИТТА КОЛЬЦО — поля k, кольцо типов квадратичных форм над k, кольцо W(k).классов невырожденных квадратичных форм на конечномерных векторных пространствах над kпо следующему отношению эквивалентности: форма f1 эквивалентна форме тогда и только тогда, когда для… … Математическая энциклопедия

ГРУППОВАЯ АЛГЕБРА — группы G над полем K ассоциативная алгебра над полем К, элементами к рой являются всевозможные формальные конечные суммы вида а операции определяются формулами: (в правой части второй формулы сумма также конечна). Эта алгебра обозначается… … Математическая энциклопедия

Делитель нуля

В кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.

Аналогично, элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.

Элемент, который одновременно является и правым, и левым делителем нуля, называется делителем нуля. Если умножение в кольце коммутативно, то понятия правого и левого делителя совпадают. Элемент кольца, который не является ни правым, ни левым делителем нуля, называется обычным элементом.

0 называется собственным (тривиальным) делителем нуля. Соответственно, элементы, отличные от нуля и являющиеся делителями нуля, называются несобственными (нетривиальными) делителями нуля.

Пример: в кольце

Источник

From Wikipedia, the free encyclopedia

In abstract algebra, an element a of a ring R is called a left zero divisor if there exists a nonzero x in R such that ax = 0,^[1] or equivalently if the map from R to R that sends x to ax is not injective.^[a] Similarly, an element a of a ring is called a right zero divisor if there exists a nonzero y in R such that ya = 0. This is a partial case of divisibility in rings. An element that is a left or a right zero divisor is simply called a zero divisor.^[2] An element a that is both a left and a right zero divisor is called a two-sided zero divisor (the nonzero x such that ax = 0 may be different from the nonzero y such that ya = 0). If the ring is commutative, then the left and right zero divisors are the same.

An element of a ring that is not a left zero divisor is called left regular or left cancellable. Similarly, an element of a ring that is not a right zero divisor is called right regular or right cancellable.
An element of a ring that is left and right cancellable, and is hence not a zero divisor, is called regular or cancellable,^[3] or a non-zero-divisor. A zero divisor that is nonzero is called a nonzero zero divisor or a nontrivial zero divisor. A nonzero ring with no nontrivial zero divisors is called a domain.

Examples[edit]

One-sided zero-divisor[edit]

Consider the ring of (formal) matrices ${begin{pmatrix}x&y\0&zend{pmatrix}}$ with and . Then ${begin{pmatrix}x&y\0&zend{pmatrix}}{begin{pmatrix}a&b\0&cend{pmatrix}}={begin{pmatrix}xa&xb+yc\0&zcend{pmatrix}}$ and ${begin{pmatrix}a&b\0&cend{pmatrix}}{begin{pmatrix}x&y\0&zend{pmatrix}}={begin{pmatrix}xa&ya+zb\0&zcend{pmatrix}}$ . If , then ${begin{pmatrix}x&y\0&zend{pmatrix}}$ is a left zero divisor if and only if is even, since ${begin{pmatrix}x&y\0&zend{pmatrix}}{begin{pmatrix}0&1\0&0end{pmatrix}}={begin{pmatrix}0&x\0&0end{pmatrix}}$ , and it is a right zero divisor if and only if is even for similar reasons. If either of is , then it is a two-sided zero-divisor.
Here is another example of a ring with an element that is a zero divisor on one side only. Let be the set of all sequences of integers ${displaystyle (a_{1},a_{2},a_{3},...)}$ . Take for the ring all additive maps from to , with pointwise addition and composition as the ring operations. (That is, our ring is , the endomorphism ring of the additive group .) Three examples of elements of this ring are the right shift ${displaystyle R(a_{1},a_{2},a_{3},...)=(0,a_{1},a_{2},...)}$ , the left shift ${displaystyle L(a_{1},a_{2},a_{3},...)=(a_{2},a_{3},a_{4},...)}$ , and the projection map onto the first factor ${displaystyle P(a_{1},a_{2},a_{3},...)=(a_{1},0,0,...)}$ . All three of these additive maps are not zero, and the composites and are both zero, so is a left zero divisor and is a right zero divisor in the ring of additive maps from to . However, is not a right zero divisor and is not a left zero divisor: the composite is the identity. is a two-sided zero-divisor since , while is not in any direction.

Non-examples[edit]

The ring of integers modulo a prime number has no nonzero zero divisors. Since every nonzero element is a unit, this ring is a finite field.
More generally, a division ring has no nonzero zero divisors.
A nonzero commutative ring whose only zero divisor is 0 is called an integral domain.

Properties[edit]

In the ring of n-by-n matrices over a field, the left and right zero divisors coincide; they are precisely the singular matrices. In the ring of n-by-n matrices over an integral domain, the zero divisors are precisely the matrices with determinant zero.
Left or right zero divisors can never be units, because if a is invertible and ax = 0 for some nonzero x, then 0 = a⁻¹0 = a⁻¹ax = x, a contradiction.
An element is cancellable on the side on which it is regular. That is, if a is a left regular, ax = ay implies that x = y, and similarly for right regular.

Zero as a zero divisor[edit]

There is no need for a separate convention for the case a = 0, because the definition applies also in this case:

If R is a ring other than the zero ring, then 0 is a (two-sided) zero divisor, because any nonzero element x satisfies 0x = 0 = x0.
If R is the zero ring, in which 0 = 1, then 0 is not a zero divisor, because there is no nonzero element that when multiplied by 0 yields 0.

Some references include or exclude 0 as a zero divisor in all rings by convention, but they then suffer from having to introduce exceptions in statements such as the following:

In a commutative ring R, the set of non-zero-divisors is a multiplicative set in R. (This, in turn, is important for the definition of the total quotient ring.) The same is true of the set of non-left-zero-divisors and the set of non-right-zero-divisors in an arbitrary ring, commutative or not.
In a commutative noetherian ring R, the set of zero divisors is the union of the associated prime ideals of R.

Zero divisor on a module[edit]

Let R be a commutative ring, let M be an R-module, and let a be an element of R. One says that a is M-regular if the «multiplication by a» map is injective, and that a is a zero divisor on M otherwise.^[4] The set of M-regular elements is a multiplicative set in R.^[4]

Specializing the definitions of «M-regular» and «zero divisor on M» to the case M = R recovers the definitions of «regular» and «zero divisor» given earlier in this article.

Notes[edit]

^ Since the map is not injective, we have ax = ay, in which x differs from y, and thus a(x − y) = 0.

References[edit]

^ N. Bourbaki (1989), Algebra I, Chapters 1–3, Springer-Verlag, p. 98
^ Charles Lanski (2005), Concepts in Abstract Algebra, American Mathematical Soc., p. 342
^ Nicolas Bourbaki (1998). Algebra I. Springer Science+Business Media. p. 15.
^ ^a ^b Hideyuki Matsumura (1980), Commutative algebra, 2nd edition, The Benjamin/Cummings Publishing Company, Inc., p. 12

Смотрите также:

Смотрите также
Калькуляторы
Последние примеры

Оцените материал:

Загрузка…

Источник

Делитель нуля

В общей алгебре элемент кольца называется левым делителем нуля, если существует ненулевое такое, что ab=0 .

Аналогично, элемент кольца является правым делителем нуля, если существует ненулевое такое, что ba=0 .

Пример: если k не взаимно просто с n, то класс эквивалентности числа k является делителем нуля в кольце вычетов . Например, в кольце ${mathbb Z}_{6}$ элементы 2, 3, 4 — делители нуля.

Коммутативное кольцо с единицей 1neq 0 без нетривиальных делителей нуля называется целостным, или областью целостности. Например, кольцо целых чисел — целостное кольцо.

Ссылки

Hazewinkel, Michiel, ed. (2001), «Zero divisor», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Michiel Hazewinkel; Nadiya Gubareni; Nadezhda Mikhaĭlovna Gubareni & Vladimir V. Kirichenko. (2004), Algebras, rings and modules, vol. Vol. 1, Springer, ISBN 1-4020-2690-0
Weisstein, Eric W. Zero Divisor (англ.) на сайте Wolfram MathWorld.

Источник

Кольцо с единицей

Из определения
кольца не вытекает существование или
отсутствие в нем единицы е. Но, как
было доказано в алгебре на I
курсе, если в кольце К единичный
элемент существует, то только один. В
нулевом кольце

,
состоящем только из одного нуля, элемент
0 одновременно является и единицей,
т.к.

.

Определение.
Нулевое кольцо К, в котором есть
единичный элемент е, называется
кольцом с единицей.

Примерами колец
с единицей являются: кольцо целых чисел
Z; кольцо рациональных
чисел Q; кольцо
действительных чисел R;
кольцо комплексных чисел С; кольцо
матриц n-го порядка над
полями R, Q,
C, единицей этих
колец является матрица

Примерами кольца,
в котором нет единицы, служит кольцо
целых чисел, кратных произвольно
выбранному натуральному числу m>1;
в частности, нет единицы в кольце четных
целых чисел.

Пусть К –
произвольное кольцо с единицей е.
Для всякого отличного от нуля элемента
а
К
справедливы равенства

Отсюда следует,
что

.

Если для элемента
а
К
в кольце К существует обратный
элемент а^-1, то только один.
Элемент е является обратным для
самого себя. Из равенства

следует, что элемент – е также
является обратным для самого себя.
Элемент 0 не имеет обратного элемента,
т.к.

для любого а
К.
Если для а
К
в кольце К существует обратный
элемент а^-1, то а , по
определению делителей элемента кольца,
является делителем e,
т.к.

.

Поэтому можно
принять такое определение.

Определение
2. Элемент а, для которого в
кольце К существует обратный элемент
а^-1, называется обратимым
или делителем единицы.

Пример.
Кольцо Z является
самым простым примером коммутативного
кольца, в котором только 1 и -1 являются
делителями единицы.

Теорема 3. Множество
К^* всех делителей единицы
кольца К является группой по
умножению.

□ Пусть элементы

,
т.е. являются делителями единицы е.
Значит

и

,
а это значит, что а^-1 и ab
тоже являются делителями е, а, значит,
содержатся в К^*, е также
содержится в К^*. Поэтому
К^* является мультипликативной
группой.

Группа К^*
называется группой делителей единичного
элемента, или группой обратимых
элементов кольца К.■

Делители нуля. Область целостности

Пусть К –
произвольное кольцо. Для

выполняется равенство

.
Следовательно, каждый элемент кольца
является делителем нуля. Но в теории
колец принимают следующее определение
делителей нуля.